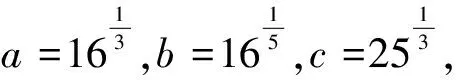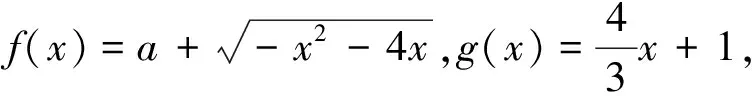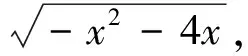例析小题巧做之图像法解题

江西师大数信学院 (330022) 严 婷

图像法是借助函数图像的直观性来处理有关代数问题的方法，体现的是数形结合的数学思想.高考数学中的选择、填空类小题常以此法为落脚点考察学生对数形结合方法的应用.借助图像法解题,不仅可以避免繁琐的运算,达到事半功倍的效果，而且还能加深学生对数学基本概念的理解，对基本知识与基本技能的灵活运用.本文撷取几例，予以说明.

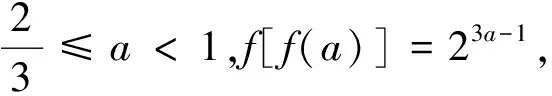
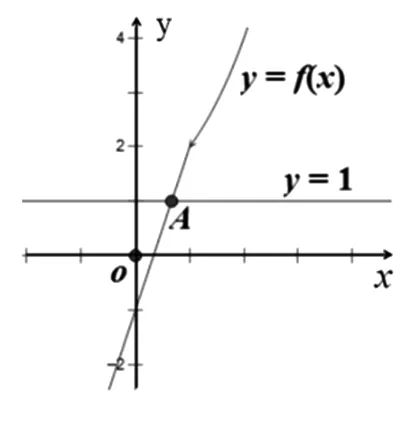
图1

例2 对任意实数x，设f(x)=min {4x+1，x+2,-2x+4}，则f(x)的最大值是 .

图2

评注：法一用代数法求解，运用了分类讨论的思想，但在分类过程中，学生需十分谨慎细心，否则易因漏分或错分而得不到正确答案.法二运用图像法，较之法一巧妙地避免了复杂的分类讨论，而且从图像的高低可以直观的看出所对应的函数值的大小，达到事半功倍的效果.

图3

A.b

C.b

评注：要比较a,b,c三者的大小，首先应把它们变形为同底数或同指数的形式，但由于我们最多只能统一两个数的形式，这时在此基础上利用函数图像，便能快速得出三者的大小关系，使问题迎刃而解.

图4

解：设h(x)=

f(x)≤g(x)恒成立，则只能将h(x)向下移动，当半圆恰好与直线相切时，结论成立.

评注：对于不等式恒成立的问题，我们常用的方法有构造函数法，分离变量法，图像法等.但在选择、填空类题求解可以优先考虑图像法，尤其是易于画出给定函数图像的题，它可以省去繁琐的计算步骤，使复杂问题简单化.

例5 已知定义域为R的奇函数f(x)满足f(x)+f(2-x)=0,且当x∈[-1,0)时，f(x)=

A.2B.3C.4D.6

图5

解：由题意可知，f(x)是周期为2的奇函数，方程变形为f(x)=g(x)-1，令h(x)=g(x)-1，则题目转化为求在[-3,3]上函数f(x)与h(x)图像的交点个数，画出图像如图5，则由图像可以直观看出有A,B,C三个交点，故选B.

评注：这是与周期函数，奇偶函数结合的一道求方程解的个数问题.显然，用代数法无法求解，但若把方程根的个数问题转化为函数图像的交点个数问题，运用图像法便能天堑变通途，将题目解出.

综上，图像法在解部分选择、填空类题时，总会给我们带来意想不到的快捷与高效.所以，要想学生能够灵活的运用图像法解题，那么老师上课时就应该足够重视基本函数图像的性质与画法，并让学生熟练的掌握图像的平移、旋转、对称等变换.