加强典型错解反思 让学困生思维继续飞翔*

(733018)

学困生的知识背景、思维方式、情感体验往往有许多欠缺，而其表达方式可能又不准确，这就难免有“错”.例题教学若能从此切入，进行解后反思，则往往能找到“病根”，进而对症下药，常能收到事半功倍的效果.本文对学困生作业中的部分典型错解加以归纳反思, 从而达到以例明理之功效,让学困生思维继续飞翔.

1.忽视隐含条件，导致结果错误.

隐含条件是指题目中没有给出的条件,需要从题设、结论或相关知识的联系上体现出来.在数学解题中,常因学困生没有注意到题目中的隐含条件,而出现解题错误,影响解题思维的提高.

例1 已知x，y≥0，2x2-3xy-y2+8x+3y-4z+2=0，2x+y-6=0,求z的取值范围.

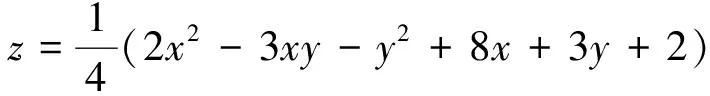
反思：上述解法虽然注意了x≥0，但忽视了隐含条件y对x的约束：y=6-2x≥0.结合x≥0知x∈[0，3]，所以z∈[-4，11].解完一道题后，应进一步思考：题目中所有条件都用过了吗？(包括括号内的条件)，题目所要求的问题解决了吗？还有没有需要增加说明和舍掉的部分等.

评注：通过这样不断地质疑、不断改进，让学困生在不断的知识联系和知识整合中，丰富认知结构中的内容，体验“创造”带来的乐趣，这对培养学困生的创造思维是非常有利的.

2.忽视等价性变形，导致错误.

不等价.

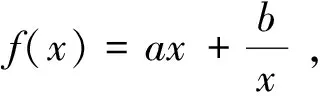
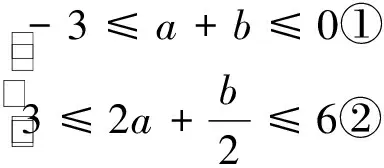
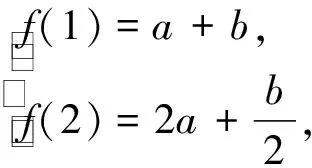
评注：在本题中能够检查出解题思路错误，并给出正确解法，就体现了思维具有反思性.只有牢固地掌握基础知识，才能反思性地看问题,学困生的思维才能得到进一步的飞跃.

3.忽视不等式等号成立的条件，导致结果错误.

基本不等式a2+b2≥2ab中，当且仅当“a=b”时等号成立.

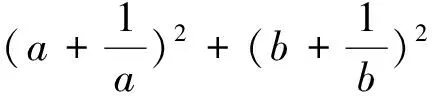
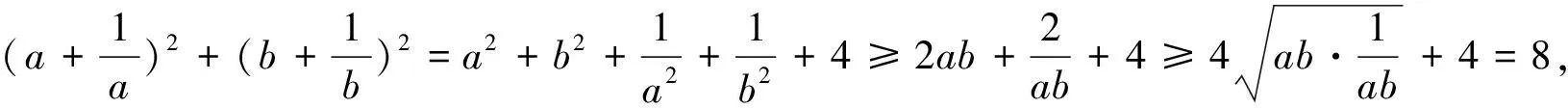
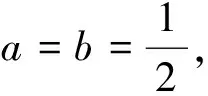
评注：学困生解数学题，不能保证一次性正确和完善,所以解题后，必须对解题过程进行回顾和评价，对结论的正确性和合理性进行验证,并且在反思过程中达到对某些知识的补漏、知识结构的优化,使得思维更加合理严密.

4.不进行分类讨论，导致错误.

分类讨论思想是指在解决一个问题时，无法用同一种方法去解决，而需要一个标准将问题划分成几个能用不同形式去解决的小问题，将这些小问题一一加以解决，从而使问题得到解决.

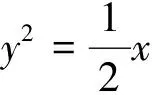
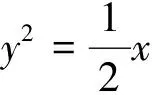
反思：(如图1,图2)显然，当a=0时，圆与抛物线有两个公共点.

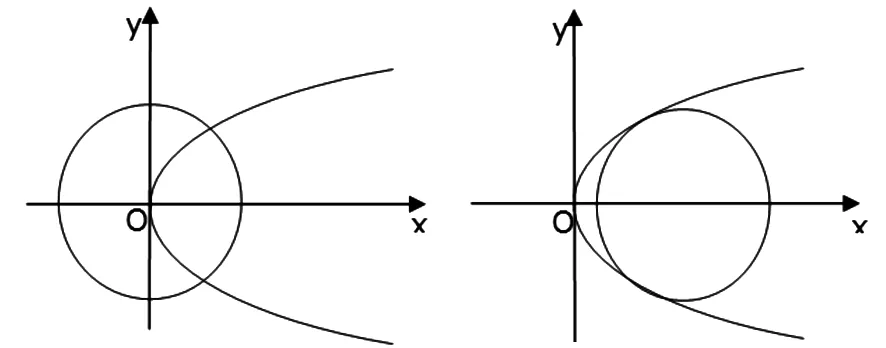
图1 图2

要使圆与抛物线有两个交点的充要条件是:方程①有一正根、一负根；或有两个相等正根.

当方程①有一正根、一负根时，得

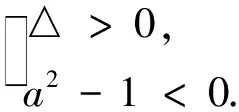
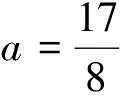
评注：通过这样的反思,使学困生进一步体会到:数学思想方法是数学的灵魂，是知识的精髓，是知识转化为能力的桥梁.“授之以鱼，不如授之以渔”，方法的掌握，思想的形成，才能使自己受益终生.

5.以偏概全，导致错误.

以偏概全是指思考不全面，遗漏特殊情况，致使解答不完全，不能给出问题的全部答案，从而表现出思维的不严密性.

例5 求过点(0,1)的直线，使它与抛物线y2=2x仅有一个交点.

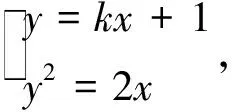
反思：此解法共有三处错误：(1)设所求直线为y=kx+1时，没有考虑k=0与斜率不存在的情形，实际上就是承认了该直线的斜率是存在的，且不为零，这是不严密的.(2)题中要求直线与抛物线只有一个交点，它包含相交和相切两种情况，而上述解法没有考虑相切的情况，只考虑相交的情况.原因是对于直线与抛物线“相切”和“只有一个交点”的关系理解不透.(3)将直线方程与抛物线方程联立后得一个一元二次方程，要考虑它的判别式，所以它的二次项系数不能为零，即k≠0,而上述解法没作考虑，表现出思维不严密.

正解：①当所求直线斜率不存在时，即直线垂直x轴，因为过点(0,1)，所以x=0,即y轴，它正好与抛物线y2=2x相切.

②当所求直线斜率为零时，直线为y=1平行x轴，它正好与抛物线y2=2x只有一个交点.

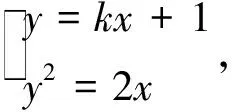
评注：通过错解后改进解题过程、探讨知识联系、知识整合、探究规律等一系列思维活动，使学困生的解题思路更加严谨、更加完整， “八方联系，浑然一体，漫江碧透，鱼翔浅底”,这是解题过程中更高一级的思维活动.

总之，解题后要反思题目提供的信息,看是否抓住了题中的关键词语,对于条件和结论有无疏漏之处，隐含条件是否挖掘出来；反思思维过程，检验解题过程的思维方式是否正确、合理、严谨，解题过程是否完善，结论是否完整，是否正确合理；反思解题中有没有需要增加说明和剔除的部分等.为了让学困生思维继续飞翔，提高解题能力，应该倡导和训练学生进行有效的解题反思.