走出直线与圆锥曲线位置关系的教学困境

福建省闽清教师进修学校 (350800) 黄如炎

1 教学现状

直线与圆锥曲线位置关系向来是解析几何的教学难点，高考的重点、热点与难点．对直线与圆锥曲线位置关系问题，教师们增加了教学课时，设计了复习专题，强化了练习考试．学生们投入了成倍学时，经历了艰难思路，进行了大量运算，但教学却毫无成效．2017年高考理科全国I卷直线与圆锥曲线位置关系的解答题是道寻常题，第二步满分7分，绝大多数考生不能得分，只有极少数考生能得1至2分[1]．劳而无功的教学使教师对解几失去信心，学生对解几产生恐惧．当教学投入与产出总不成正比时，不少教师认为直线与圆锥曲线位置关系是不可教，许多学生(包括优等生)认为直线与圆锥曲线关系是不可学．有些教师在考试策略上指导学生对直线与圆锥曲线位置关系要舍得放弃，实施“第一步确保，第二步列式”的战术，错失了解析几何承载的直观想象、数学运算、逻辑推理等核心素养的教育价值．本文从解析几何本质、圆锥曲线属性、平面几何性质和直线方程选择的视角，旨在让教师走出直线与圆锥曲线位置关系的教学困境，使直线与圆锥曲线位置关系变得教师可教，学生可学，考试可得．

2 基本思路

解析几何是把几何问题代数化，即解析法的本质是坐标法．研究直线与圆锥曲线位置关系的基本思路为：引入相关点坐标→把几何问题用坐标表示→由点所在的直线、曲线方程求出坐标或坐标关系式→通过代数运算解决问题．

3 研究经验

研究直线与圆锥曲线位置关系，除了遵循解析法的基本思路外，还要从圆锥曲线属性、平面几何性质和直线方程选择的视觉，优化研究过程．圆锥曲线定义是圆锥曲线的本源，涉及焦半径的问题利用定义直截了当．在坐标化前要考虑能否利用平几、三角、向量、定义等知识简化几何关系，坐标化过程要注意每个式子的几何意义．数与形密不可分，数形结合是优化思维性，减少运算量的利器．直线和圆锥曲线方程问题中，圆锥曲线方程相对单一，但直线方程形式多样，选择哪条直线，选择哪种形式，对计算量有很大关系，因此要根据题情判断如何优选直线方程．此外，坐标化后代数运算要遵循数式运算法则，先细致观察数式表征后实施相应运算．对同类项要展开合并，多项式要因式分解，公因式要提取，分式要通分(或去分母)，多元要消元，同一个式子要视为一个整体，去括号要注意是否变号．教师对运算要言传身教，全程示范，不能用“化简为”、“整理得”省略学生可能犯错的步骤，在板演中强调思维点、切入点、易错点、得分点．

“回归定义不可忘，数形结合成习惯，选择直线要判断，数式先看后运算”应成为研究直线与圆锥曲线位置关系的基本经验．

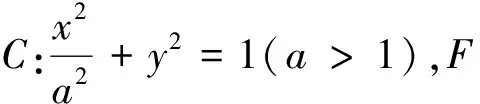
(1)求C的方程;

(2)直线l与C相交于P、Q两点，A为C的右顶点，若直线PA与直线QA斜率的倒数的和为-1，求证：l过定点．(2017年高考全国I卷理科第20题改编)

研究方法分析如下．

(1)方法1：与焦点有关的问题自然想到定义，设另一焦点为F′，四边形MFNF′对角线互相平分，故MFNF′为平行四边形，由椭圆定义知|MF′|+|MF|=|NF|+|MF|=2a，所以△MNF周长为|MN|+2a，当MN为短轴时|MN|最小，所以

2.2.2 食品防腐剂 目前，大多食品防腐剂也可用于杨梅采后病害的防治。王益光等[21]采用蔗糖酯、尼泊金乙酯、山梨酸钾和苯甲酸钠对杨梅果实进行处理，发现蔗糖酯防腐效果最好，其次是尼泊金乙酯，而苯甲酸钠和山梨酸钾的防腐效果不明显。柴春燕等[22]比较了CAP-10、山梨酸钾、尼泊金乙酯处理杨梅果实的效果，发现这些防腐剂都对杨梅采后病原菌都有不同程度的抑制作用，其中CAP-10的抑菌效果最佳，并且相比山梨酸钾和尼泊金乙酯，药液味较淡。

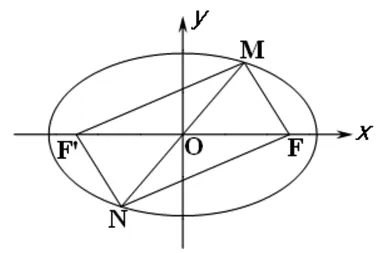
图1

方法2：三角形MNF周长由M、N、F三点坐标决定，可得研究思路：

引入点M，N，F坐标→把几何问题“△MNF周长”用坐标表示→由点M所在的椭圆方程求出坐标关系→通过代数运算解决问题．

设M(x0,y0)，N(-x0,-y0)，F(c，0),则

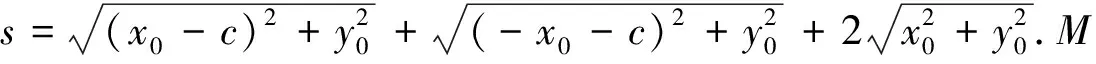
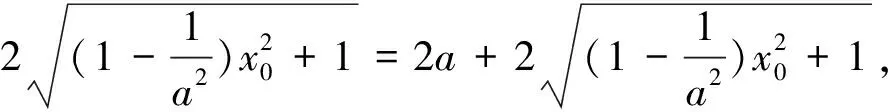
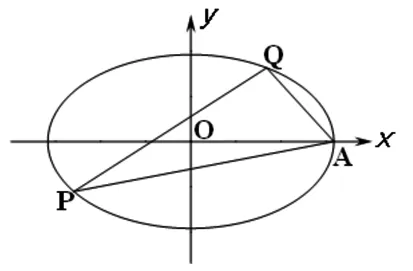
图2

(2)直线PA与直线QA斜率由点P，Q，A决定，可得研究思路：引入点P，Q坐标→把几何问题“直线PA与直线QA斜率的倒数的和”用坐标表示→由点P，Q所在的直线l(或直线PA、QA)和椭圆C方程求出坐标或坐标关系式→通过代数运算解决问题．

方法2：选取直线l：y=kx+t．当l斜率不存在即l垂直x轴时，kPA+kQA=0，不合题意．

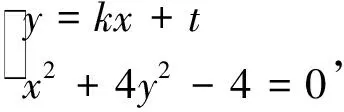
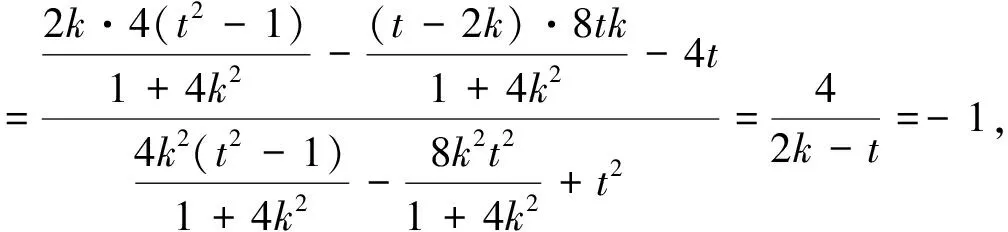
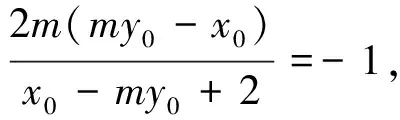
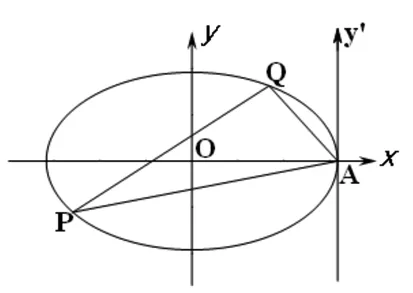
图3

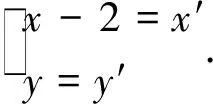
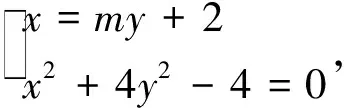
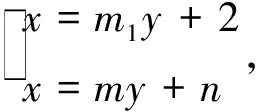
4 方法评价

第(1)步的方法1注意回归定义和数形结合，无需运算．第(2)步从直线方程不同的选取视角展开思维．方法1至方法4把P、Q看成直线l和椭圆的交点，故选择直线l，但在直线l的形式选取上决定了计算量．方法2选取l:y=kx+t，是学生的普遍做法，但消元时分母变为多项式，增加了计算量．方法3选取l:x=m(1-y0)+x0，此方程比x=my+n复杂(多一个字母和项数)，计算量明显大于方法1．方法4通过平移，转化为齐次方程，选取直线l:mx′+ny′=1，计算量虽小，但技巧性太强．方法5把P看成直线PA和椭圆交点，选取直线PA方程为x=my+2(比选取y=k(x-2)简单)，联合直线PA和椭圆C方程求出P点坐标，由对称性得出Q点坐标．由于P，Q坐标是含有字母的形式，用两点式求直线l方程时，产生了极大的计算量．方法6把P看成直线PA和直线l的交点，联合直线PA、l方程求出P点坐标，再把P坐标代入椭圆方程整理成关于m1的一元二次方程，由对称性和韦达定理得出m，n关系式，此法运算量适中但也颇具技巧性．

综上可见，方法1最适合学生，思路朴实，运算顺畅，计算量小，能限时完成．教师要善于寻找适合学生的方法，创造适合学生的教育，落实以学生发展为本的新课程理念．

[1]匡大章，吕小东．由2017年安徽省高考数学阅卷引发的教学思考[j]．中学数学教学参考：上旬，2017(11)：44-46．

[2]中华人民共和国教育部制定.普通高中数学课程标准[M].北京：人民教育出版社，2017.