从代数角度研究函数图像变换问题

陕西省西安市高新第一中学 (710065) 汪仁林陕西省咸阳市乾县第一中学 (713300) 姚利娟

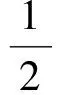
最近笔者在上这节课时，引导学生从代数的角度研究图像变换，有了新的收获，现展现出来，与读者交流.

一、教学策略

因为函数图像是由点构成的，在研究图像变换过程中，紧扣“研究图像的变换规律实际上就是研究图像上每个点的变化规律”这一本质来进行教学，先重点研究了参数φ对y=sin(x+φ)图像的影响，初步感悟欲研究函数图像的变换规律，只需研究图像上每个点坐标的变化规律，进而让学生类比已有的研究方法，自主探究另两个参数对函数图像的影响，再研究含三个参数的图像变换综合问题，最后将方法和规律推广到一般函数中去.

二、教学实录

1.研究y=sin(x+φ)与y=sinx图像的关系

研究函数图像的关系，其实就是研究图像上点的关系，如果我们设函数y=sinx图像上任意一点坐标为M(x0,y0)，这就说明sinx0=y0，由x+φ=x0得x=x0-φ.所以函数y=sin(x+φ)的图像必定过M′(x0-φ,y0).容易知，点y=sinx可看成是由点M(x0,y0)向左(φ>0)或向右(φ<0)平移|φ|个单位得到.所以函数y=sin(x+φ)图像是由函数y=sinx图像向左(φ>0)或向右(φ<0)平移|φ|个单位得到.

由上述规律可以发现，左右平移变换可以利用对比零点位置来轻松解决，例如，函数y=sinx的一个零点为x=0，由x+φ=0可得到函数y=sin(x+φ)与其对应的一个零点为x=-φ，比较0和-φ在数轴上的位置，就可轻松得到函数y=sin(x+φ)的图像是由函数y=sinx图像向左还是向右平移|φ|个单位得到.

2.研究y=Asinx与y=sinx图像的关系

学生分组合作，运用刚学的研究方法，来研究y=Asinx与y=sinx图像的关系，概括总结一般规律.类比上述方法，设函数y=sinx图像上任意一点坐标为M(x0,y0)，则函数y=Asinx的图像必定过M′(x0,Ay0)，对比M(x0,y0)和M′(x0,Ay0)两点坐标可知，函数y=Asinx的图像是由函数y=sinx图像上所有点横坐标不变，纵坐标变为原来A倍得到.

3.研究y=sinωx(ω>0)与y=sinx图像的关系

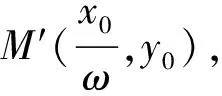
4.研究y=sinωx(ω>0)与y=sin(ωx+φ)图像的关系

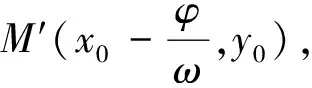
5.研究y=sinx与y=Asin(ωx+φ)(A>0,ω>0)图像的关系

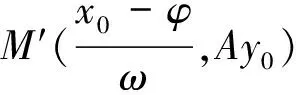
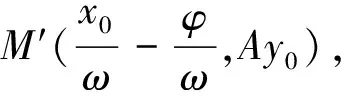
6.研究y=f(x)与y=Af(ωx+φ)(A>0,ω>0)图像的关系

由以上推导规律可知，从代数角度(坐标)研究函数图像变换对任意函数都适合，所以函数y=Af(ωx+φ)(A>0,ω>0)图像可由函数y=f(x)图像按上述方案①或方案②变换得到.

三、教后反思

从学生的课堂练习与课后作业效果来看，学生能够抓住图像上任意一点坐标的变化关系正确解答图像变换问题，且对图像的变换本质能够深刻理解，起到了事半功倍的效果！

本节课从代数角度(坐标变化关系)研究图像变换，抓住了图像变换的本质，使学生能够知其然且知其所以然，真正做到“变教教材为用教材”.如果从代数角度研究完图像变换规律后再能借助几何画板进行动态演示验证，教学效果会更好！

[1]刘聪胜、汪仁林.重视思想生成体验,打造高效课堂——“正弦函数的性质”(第一课时)教学案例[J].中国数学教育，2014(1-2)：74-78.