从两道高考姊妹题看求二元函数最值问题解答

贵州省毕节市梁才学校 (551700) 熊福州

求二元函数t=G(x,y)的最值问题，常见两类，第一类是无约束条件F(x,y)=0或F(x,y)≤0的，如t=x2+y2(x,y∈R)，t=x2+y2(x≥1,y≥2)，解答第一类问题用文[1])的两个方法(特殊的化为一元函数求最值，一般的认一元(自变量)定一元(参数)，逐步求最值)，第二类是有约束条件F(x,y)=0或F(x,y)≤0的，如t=x2+y2(x+y=2)，t=x2+y2(x+y≤2)，t=x2+y2(x≥0,y≥1,x+y≤2).现行高中教科书中的线性规划(t=G(x,y)，F(x,y)=0或F(x,y)≤0全是二元一次)与非线性规划属于第二类，在第二类中，t=G(x,y)(F(x,y)=0)的最值(值域)是非常基础而普遍的数学问题(因其余情形都可转化为这种情形)，是高考竞赛中的热点和难点，这类问题的本质是方程(组)的实解集(文[2])，这类问题直接的表述：已知F(x,y)=0，求G(x,y)的取值范围(最值)，本质是求t=G(x,y)(F(x,y)=0)的最值(值域).第二类问题的一般解法是换元，转化为一元函数求最值，特别的可数形结合法或不等式法.

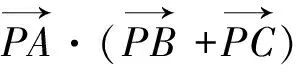
注：例1是没有约束条件F(x,y)=0或F(x,y)≤0的二元函数t=G(x,y)求最值，由于化不成一元函数求最值，故用通法认一元(自变量)定一元(参数)，逐步求最值.

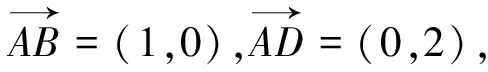
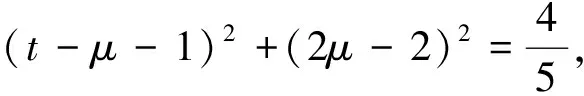
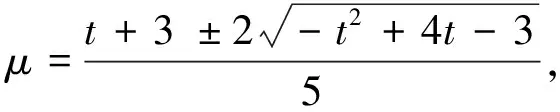
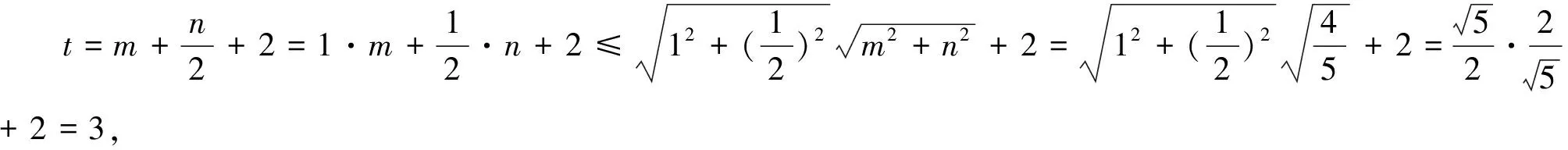
注：例1，例2是姊妹题，都是二元函数t=G(x,y)求最值，只是例1无约束条件方程,例2有约束条件方程.

[1]熊福州由2010年高考四川理(12)看多元函数最值问题的解法[J].中学数学研究(江西)，2010,10.

[2]熊福州,张龙跃.数学问题的根基本质是方程的解集[J].中学数学研究(江西)，2015，8.