一种会聚区声场基于参数化表征的方法研究∗

2018-05-29吕琳冯达

舰船电子工程 2018年5期

吕琳冯达

（91388部队91分队湛江 524022）

1 引言

会聚区现象是一种特殊形式的深海声道波导传播引起的，根据Hale的描述［1］，从海面附近声源发出的声波在深海中折射并发生反转，约在30～35海里以外的范围折回海面，形成几公里宽的环带状高声强区域，即为会聚区。会聚区中的声波具有较高的强度，这对于在大洋中的远程警戒、打击具有十分重要的意义［2］。潜艇在深海活动经常在具有会聚区形成条件的海区发现目标，由于目标方位变化缓慢，这给获得目标距离等其他信息带来了很大的困难，无法确定目标是否为会聚区目标，无法进行有效的攻防决策。关于会聚区方面的研究，主要集中在会聚区环境特点、会聚区声传播理论等，针对会聚区目标声场特征进行会聚区目标判定方面的研究较少，近年来有学者［4］利用声场的干涉现象进行深海会聚区和影区的特性分析，对会聚区目标的判定具有一定的指导意义。本文试图从会聚区声传播特性的另一个角度入手，分析会聚区声场特征，希望通过对声场的参数化表征，获得会聚区目标判定的某些理论依据。

2 深海波导简正波声场特征

深海典型的声速剖面为“三层结构”型，存在一个声速最小声道轴，由于声线被限制在海面和海底之间，在水中反转时没有能量损失，故能在深海中进行远距离传播，形成会聚区现象。简正波理论是分析和计算声场的重要理论方法，在描述声场特征时具有物理概念清晰，数学表达明确等优点。

假设海水为水平无变化介质，波动方程在海面和海底边界条件下，远场解析解［5］为

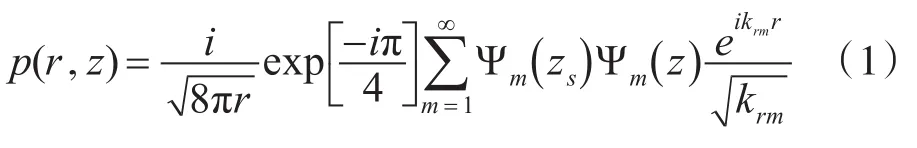
其中p(r,z)表示接收处声压，z、zs分别为接收处和声源深度，r为水平距离，Ψm为特征函数，krm为特征值。

实际深海波导中，水体中仅存在有限号简正波，高号简正波被”截止”［6］，式（1）重新表达为

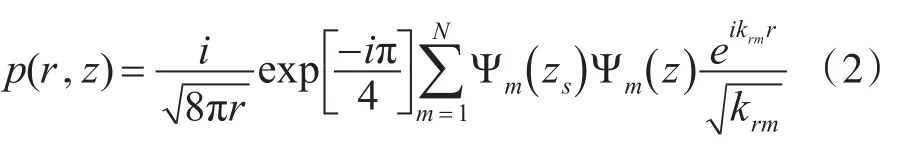
其中，N表示简正波最大号数，由W.K.B.模态条件确定。对于典型的深海声道，A.O.WILLIAMS曾经给出了简单估算N的公式［7］：

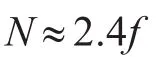
假设声源频率为1KHz，水体中的简正波个数N≈2400，因此深海中参与传播的简正波个数往往很多。这与浅海有很大不同。由于深海声场简正波个数较多，且不同簇的简正波具有各不相同的干涉特征，在此首先将典型深海波导（不考虑表面声道）的简正波进行分族［8］。对于冬季波导，其常见声速剖面如图1所示。可根据水平波数对简正波分簇，当声源信号频率为100Hz，根据图1的参数，计算得到相邻号简正波的干涉跨度如图2所示。

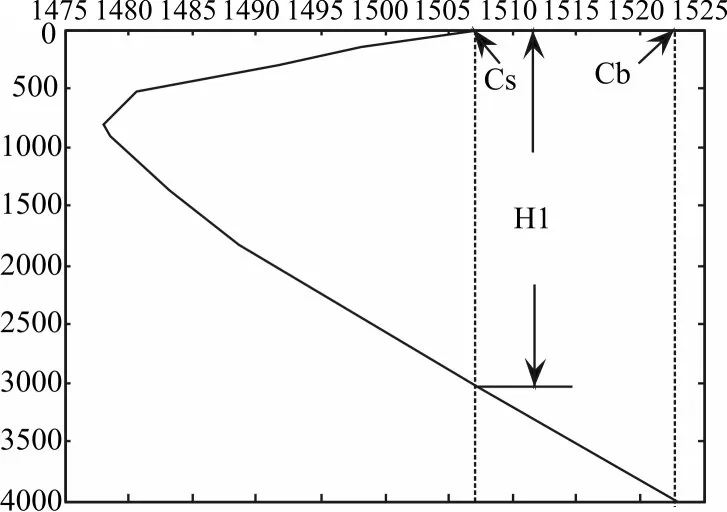
图1 冬季典型深海声速剖面

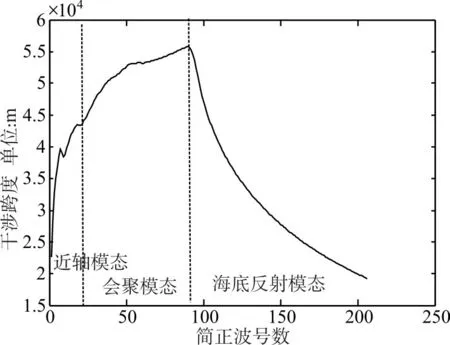
图2 相邻号简正波的干涉跨度

根据图2可知，中间号段“会聚模态”的干涉跨度为45km～55km，恰好与会聚区的距离间隔吻合。因此利用简正波理论对深海会聚区声场进行分析，可能为会聚区目标的判定提供一些可靠的判据。

3 会聚区声场的参数化设计

在分析会聚区声场时，我们在此忽略不参与会聚的简正波贡献，令参与会聚的一簇简正波初始号为m0族内共有n0号简正波，探讨会聚区声场在水平方向的干涉起伏可将式（2）做如下代换：

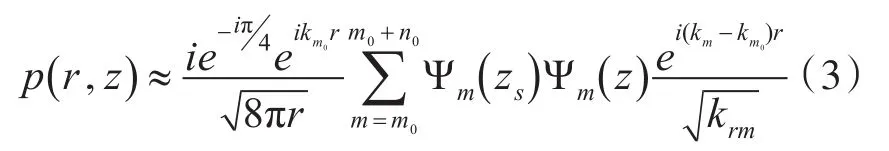
由式（3）求和号里面的表达式可以看出，声场在距离r处的声强起伏特征主要由水平方向的波数差以及深度方向上的本征函数决定。当仅考虑水平方向上的干涉起伏时，声压振幅的起伏量主要由波数差影响，由于任意两号简正波存在波数差，总声场表现为随水平距离干涉起伏。由于会聚模态的相邻两号简正波波数差随号数为非均匀分布，导致在不同的会聚区内各号简正波干涉贡献不同，将会表现出不同的特征差异［9～10］。我们拟用一曲线函数来描述水平波数差起伏，假定用简正波号数为自变量拟合出的相邻两号简正波的水平波数差为

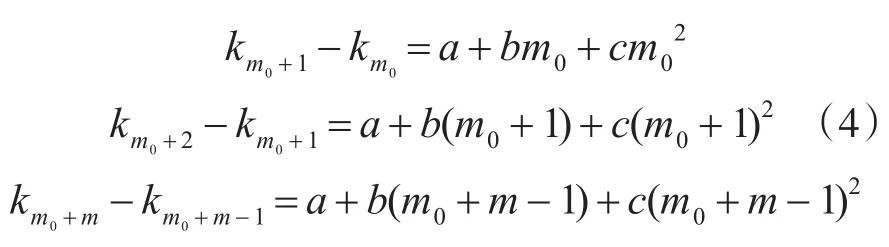
则

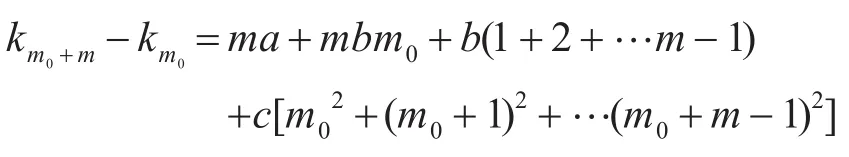
整理后得到

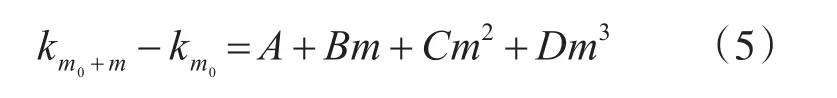
其中

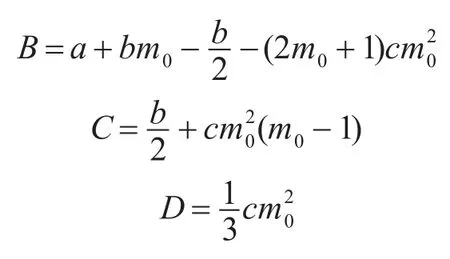
下面我们分别讨论曲线函数中的系数a，b，c的贡献，以此描述会聚区特征相似性和差异性。

假设式（4）中b=0，c=0，会聚区内模态km+1-km=a，式（3）可写为如下形式：

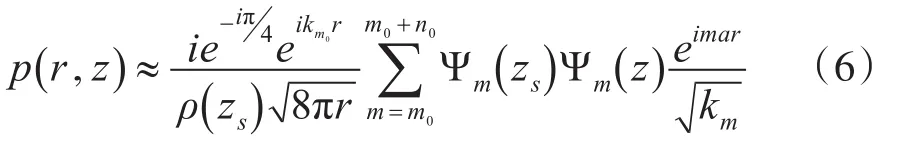
为讨论问题方便，暂不考虑式（3）求和号前面的衰减系数，根据离散傅里叶变换的周期特性可知，得到水平距离上的声强［11］分布如图3所示。

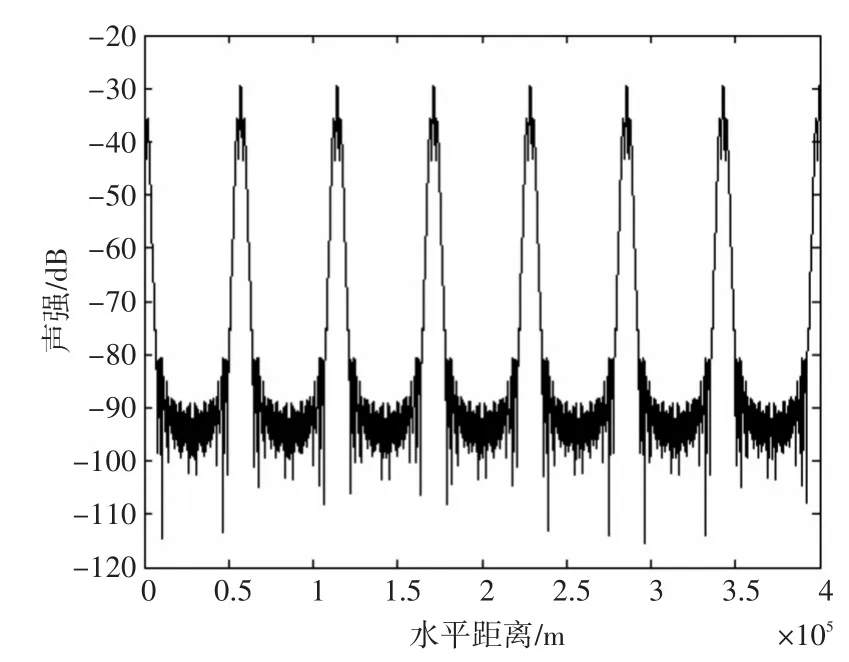
图3 会聚模态的波数差用a拟合后求的声强分布

从图3可以看出，当只存在系数a时，会聚区表现为严格的周期特性，各个会聚区未出现展宽和差异。

假设式（4）中 c=0，会聚区内模态km+1-km=a+bm为m的一次函数。此时，式（3）可写为如下形式：

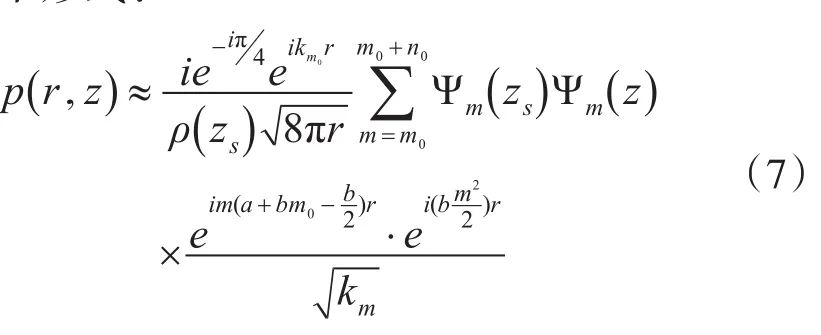
相当于在r域卷积了一项类高斯函数，这一项使会聚区展宽，且随水平距离r增大，会聚区越来越宽。如图4所示，由于m2项的存在，会聚区不再具备严格的周期性，表现为会聚区随距离展宽并在会聚区内存在起伏。

假设式（4）中会聚区内模态km+1-km=a+bm+cm2为m的二次函数。此时，式（3）可写为如下形式：

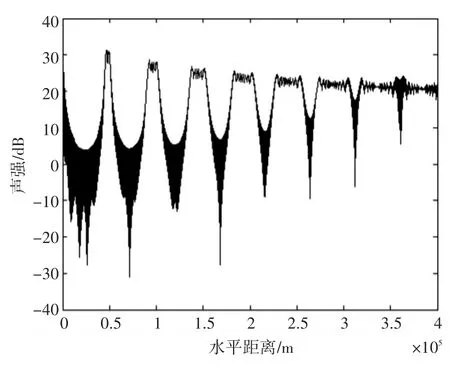
图4 会聚模态的波数差用a和b拟合后求的声强分布

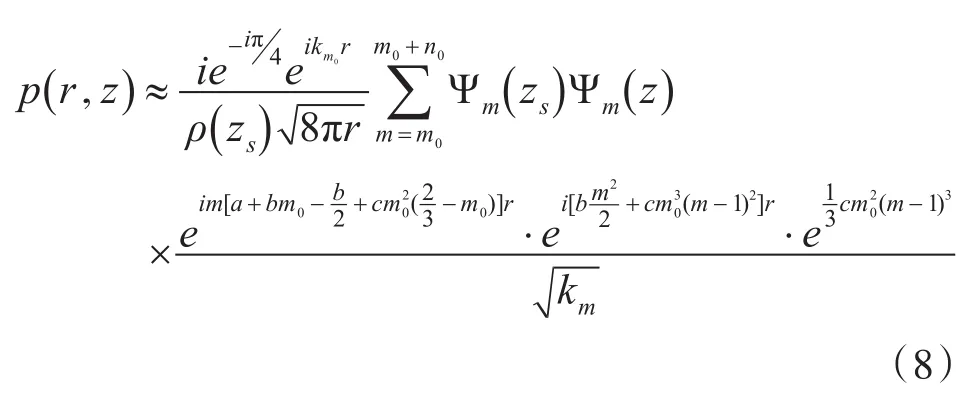
m的二次项使会聚区展宽，m的三次项导致波形不对称，出现峰侧倾现象［12］。如图5所示。

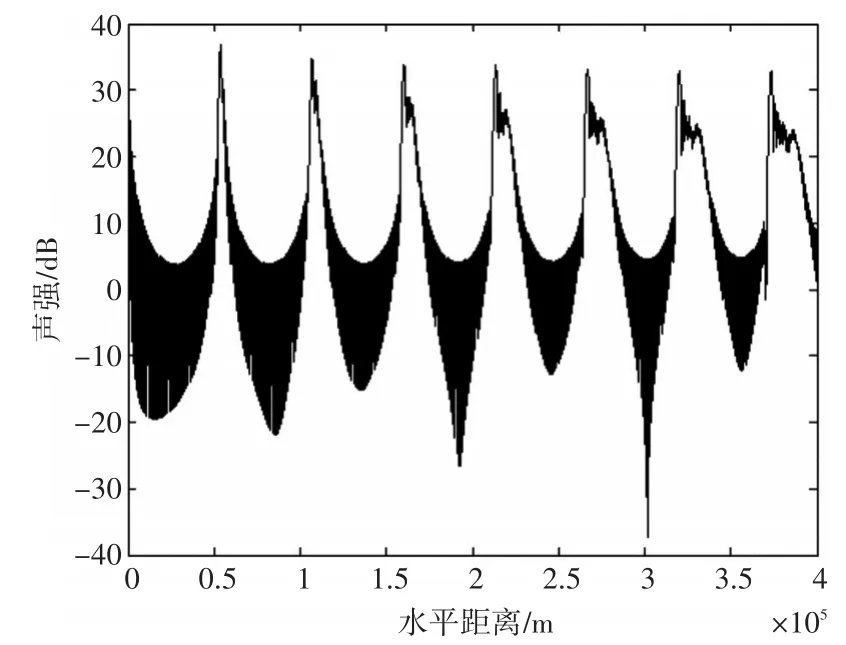
图5 会聚模态的波数差用a、b、c拟合后求的声强分布

以上分析表明，当用a，b，c三参数来描述水平波数差的起伏，进而刻画声场的水平特征时，a，b，c三参数有明确的物理意义：a参数主要决定水平干涉跨度，b参数使会聚区展宽，c参数使每一会聚区在水平方向上不对称，出现峰侧倾现象。

在实际应用中，如果可求解波数差曲线函数表达式中的a，b，c，能够描述声场水平特性，找出会聚区与非会聚区时声场参数特征因子的差异，从而可为会聚区的判定提供参考标准。

4 声场的参数化普适性分析

为进一步考核声场的参数化普适性，现研究在不同水文条件下该参数化系数的稳定性。这里我们仅仅给出在前述典型声速剖面下的声场计算。利用波数差曲线函数中的系数a，b，c，求出会聚模态下的简正波水平波数，以此计算声场，并与kraken计算得到的声场分布比较，以此验证声场参数化的可行性，如图6所示。

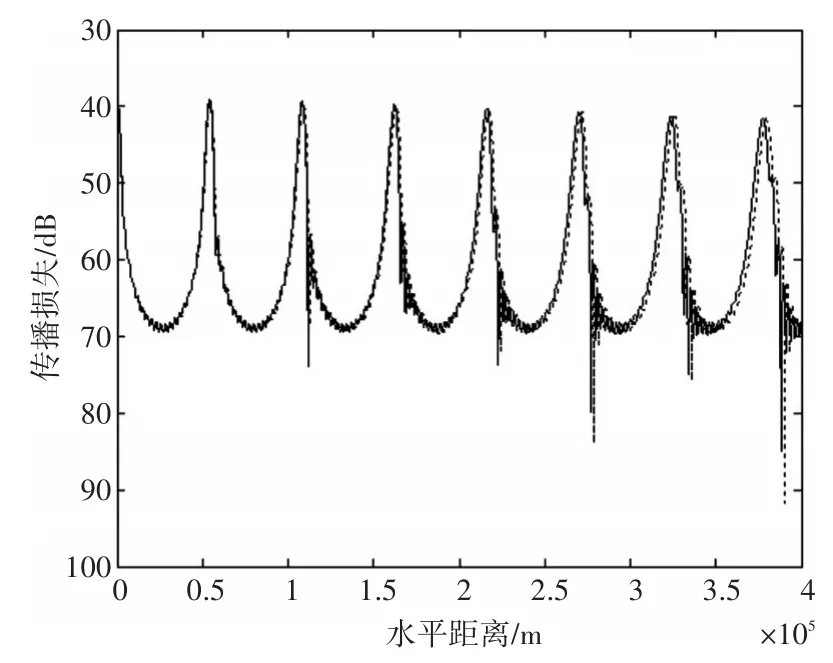
图6 声场参数化与kraken计算声强分布对比

从图6可以看出，用声场参数化方法计算出的声场传播损失和用kraken计算出的结果吻合良好，这说明声场参数化方法可很好地描述会聚区声场特征。

5 结语

本文从另外一个角度研究了会聚区声传播特性，提出利用参数化表征会聚区声场特征结构，通过上述的理论分析和计算，采用声场参数化特征因子a，b，c，可以很好地描述会聚区声场特征，且具有明确的物理意义。在实际应用中如能够根据会聚区声场特征，获得特征因子a，b，c，表征会聚区与非会聚区声场特征差异，可为会聚区目标判定提供判定依据，这也是后续将要深入研究的问题。

参考文献

［1］ F.E.Hale.Long Range Sound Propagation in the deep Ocean［J］.J.Acoust.Soc.Am.1961，33（4）：456-464.

［2］ R.J.Urick，G.R.Lund.Coherence of Convergence Zone Sound［J］.J.Acoust.Soc.Am.1968，43（4）：723-729.

［3］张仁和，何怡.大洋远程声传播理论及其应用［J］.自然科学进展，1994，4（6）：670-676.

［4］李倩倩，李整林，张仁和.利用波导不变性解释深海中的干涉现象［J］. 声学技术，2011，30（3）：13-15.

［5］Finn B.Jensen，William A.Kuperman，Michael B.Por⁃ter，Henrik Schmidt.Computational Ocean Acoustics（Sec⁃ond Edition）［M］.New York：Springer，2011.

［6］张仁和.水下声道中的反转点汇聚区简正波理论［J］.声学学报，1980，1：28-41.

［7］A.O.Williams.Normal-mode methods in propagation of underwater sound［M］.New York： R.W.B.Stephens，1970.

［8］薛福茹.深海声道会聚区的研究［J］.舰船科学技术，1982（1）：48-60.

［9］张晶晶，罗博.深海会聚区特征参数计算与分析［J］.声学与电子工程，2017（3）：8-11.

［10］范培勤，笪良龙，李玉阳.深海会聚区特征参数计算方法研究［J］. 海洋技术学报，2012，31（4）：23-25.

［11］杨刚，韩树平，黄锐.深海会聚区目标强度分析［J］.舰船科学技术，2016，38（23）：131-134.