基于Matlab的常见阵型阵增益性能仿真研究∗
2018-05-29庚张
黄 庚张 蓓
(1.海军驻大连426厂军事代表室 大连 116000)(2.杭州应用声学研究所 杭州 310023)
1 引言
在水声换能器工作时,单个点源基元是无方向性的,将多个换能器基元按一定的布阵方式装配成基阵后,基阵获得在指定方向的指向性。对于发射基阵,能使发射的声能集中在指定方向获得更远的探测距离;对于接收基阵,能改善在所期望方向的响应,提高信噪比并指明信号源的方位。相比于无指向性的点源,声基阵在指定方向上信噪比的提高称为阵增益,它是衡量声基阵性能的重要指标,也是声纳方程的重要构成。
阵增益AG(Array Gain),又称空间增益或信噪比增益,其依赖于遍布基阵的相干性,具体的值随着环境的改变而改变,常用易观察的量指向性指数DI(Directivity Index)来计算。本文重点分析这两种量之间的关系,并对常见阵型的不同束控角度、不同阵元间距下阵增益的变化做仿真研究。常见构成子阵有线阵(可简化成偶极子)、三元阵、圆环阵,现役的大部分声纳基阵都可看做这几种阵型的组合,因而对其进行阵增益研究具有较高的实用价值。
2 指向性指数DI(θ,φ) [1~2]
指向性指数描述的是波束峰值强度与平均强度的比值,具体定义如下:
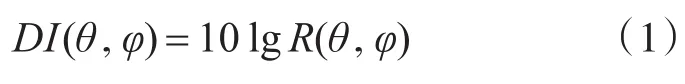
其中,指向性因数R(θ,φ)是指在远场中某一固定距离,最大响应方向上的声强Imax与各方向取平均的声强Iav之比。对于指向性函数为D( )θ,φ的阵,可按下式计算:
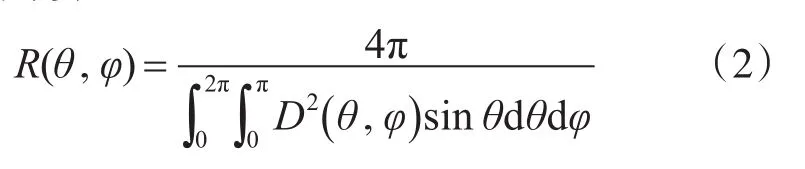
即以最大值为半径(对归一化的指向性函数最大值为1)的球体表面积与基阵的空间指向性函数的表面积之比,如图1、图2。
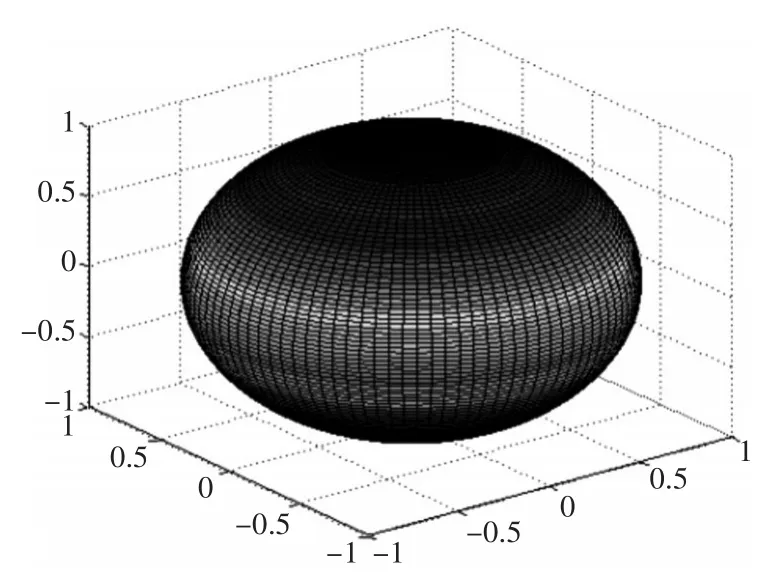
图1 无指向性阵的指向性函数示意图
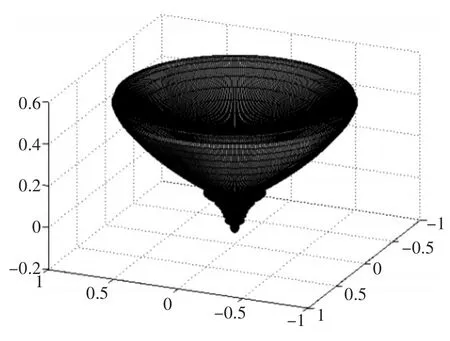
图2 具有指向性阵的指向性函数示意图
对于关于Z轴轴对称形状的阵,如xoy平面的圆面阵,Z轴上的线阵以及轴线与Z轴重合的圆柱阵,D( )
θ,φ与方位角φ无关,上式可简化为
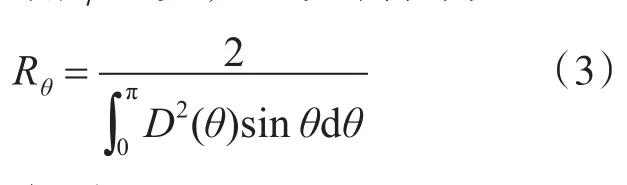
以N元线阵为例,如图3。
其不加相控补偿的垂直指向性函数[3]为
若将其束控到θ0方向上,即使主波束对准θ0方向,此时的垂直指向性函数为
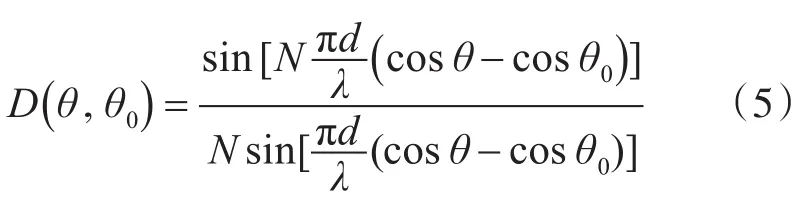
由式(14)、(15)可知决定指向性函数的参数有阵元个数N,阵元间距与波长之比(即阵元间距与接收频率),以及束控方向θ0。
3 阵增益AG
又称空间增益或信噪比增益,定义为通过基阵获得的信噪比增益,对于常规波束形成算法(CBF),即经过波束形成处理后的信噪比增加量。CBF算法模型为“延时-求和-平方均值”,如图4。
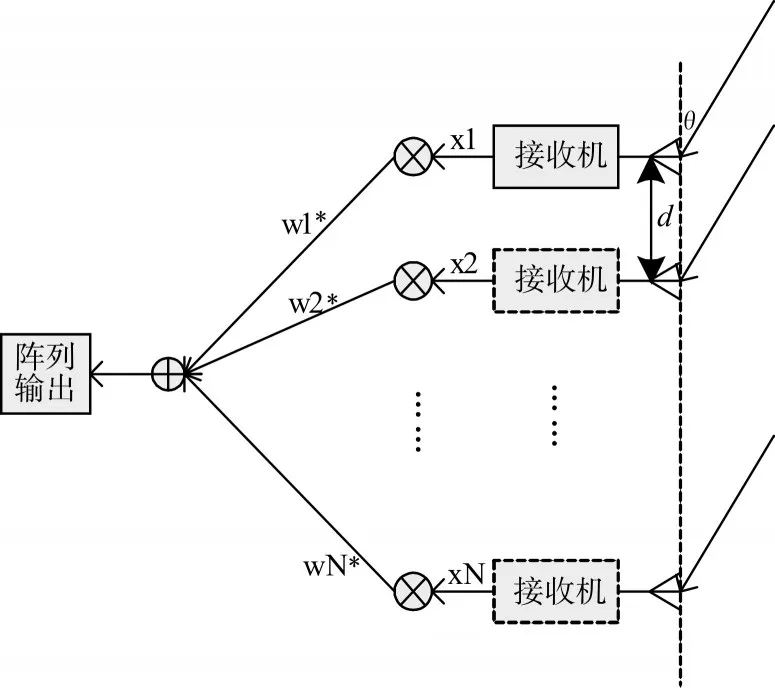
图4 波束形成示意图
阵增益AG表达式如下:
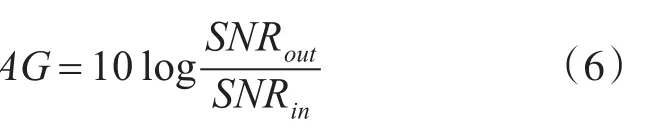
用W()θ表示权矢量,A(θ0)表示信号的方向矢量,Rn表示噪声协方差矩阵,表示噪声平均输入功率,则有
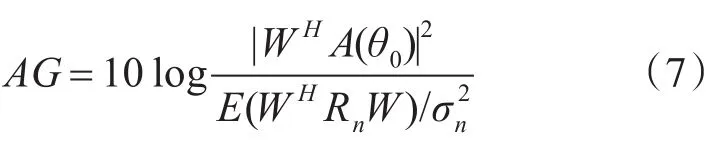
对于常规波束形成模型,在主极大方向上,W(θ0)=A(θ0)
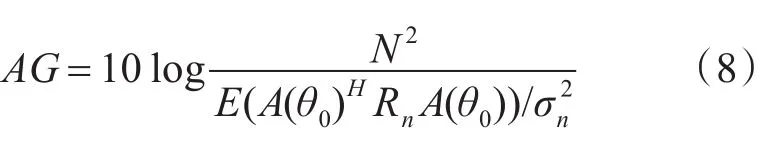
其中,Rn为归一化的噪声协方差矩阵。
由式(7)、(8)可知,决定阵增益AG的参数有阵元个数N,阵元间距与波长之比、束控方向θ0(决定方向矢量A(θ0))以及噪声的相关特性(决定协方差矩阵Rn)。
下面就常见的几种噪声模型[4~5],分析其阵增益特性:
·空间不相关高斯白噪声;
·平面波干扰噪声;
·各向均匀同性噪声场。
1)高斯白噪声
各阵元接收噪声为独立同分布的高斯白噪声,即各阵元接收的噪声之间不相关,且噪声是均值为0,方差为的随机噪声,此时有噪声的协方差矩阵
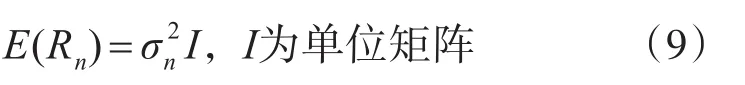
代入式(2~3)有:
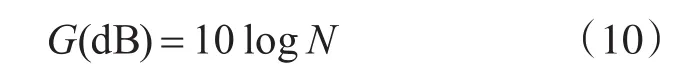
2)平面波干扰噪声
此时噪声作为特定方向上的干扰存在,实际工程中通常在波束形成中进行干扰抑制,在此不做讨论。
3)各向均匀同性噪声场
各向均匀同性噪声模型,可认为各阵元的接收噪声是各个方向来的平面的叠加,经计算得到噪声的协方差矩阵为
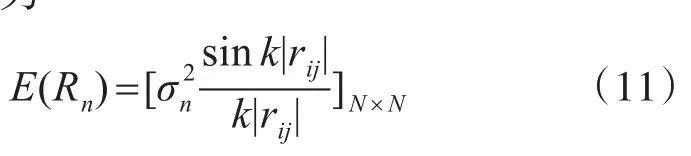
其中,λn为噪声频率对应的波长,rij为第i号阵元与第j号阵元的间距。噪声相关性表现为sinc函数特性。
此时,阵增益为
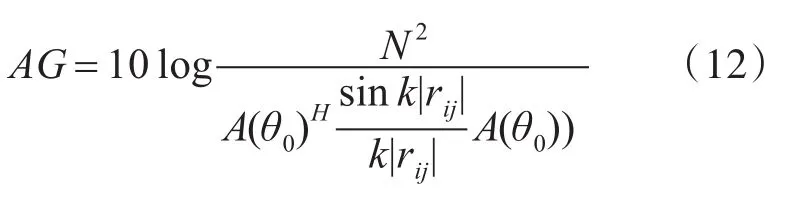
从两者的定义上不难发现,DI是AG的一种简化模型,等效于各向均匀同性且与信号同频的噪声场下的阵增益。
4 常见阵型阵增益研究
这里研究三种常见阵型——均匀线阵[6~8],三元阵[9],均匀圆环阵[10],其阵坐标示意图如下:
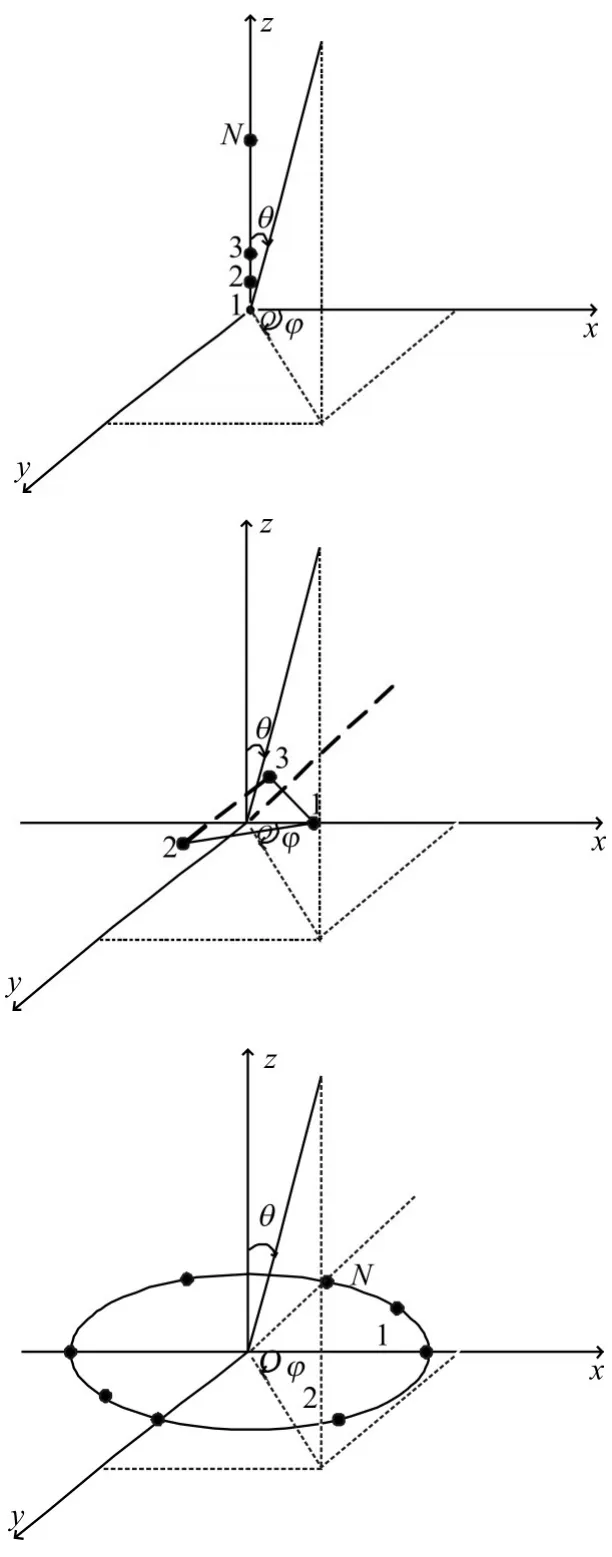
图5 三种常见阵型的阵坐标示意图
4.1 不同间距下的阵增益
三种阵型下,不加束控时,分别计算指向性指数DI与各向同性均匀噪声场下的阵增益AG。
1)10元均匀线阵,阵元间距d,波长λ,根据指向性函数D(θ,φ)由式(2)计算指向性指数DI,另一方面根据式(12)计算阵增益AG,两者随间距的改变如图6。
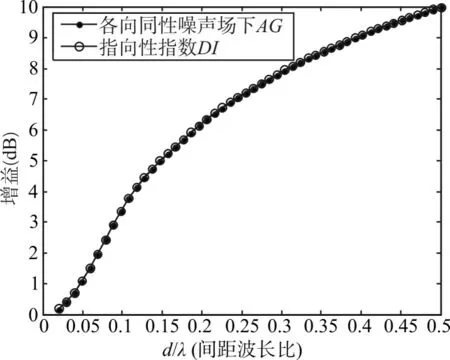
图6 10元线阵DI与AG随d/λ的变化
2)三元阵,阵元间距d,波长λ,根据指向性函数由式(2)计算指向性指数DI,另一方面根据式(12)计算阵增益AG,两者随间距的改变如图7。
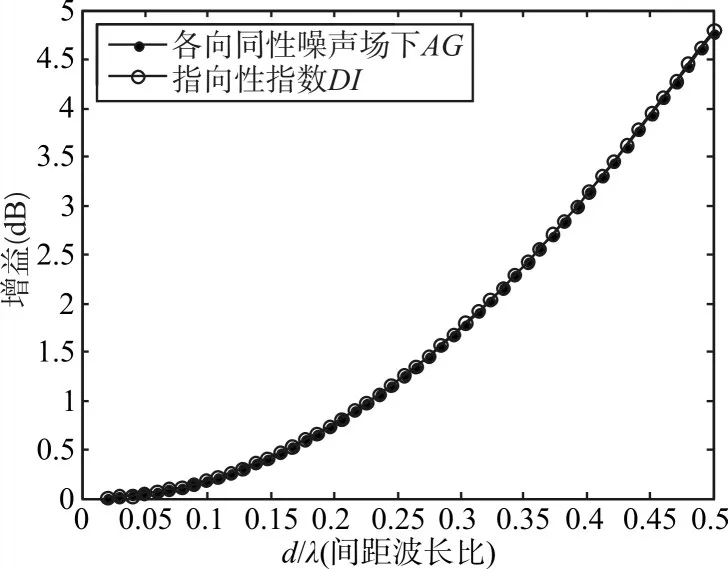
图7 三元阵DI与AG随d/λ的变化
3)10元圆环阵,阵元间距d,波长λ,根据指向性函数由式(2)计算指向性指数DI,另一方面根据式(12)计算阵增益AG,两者随间距的改变如图8。
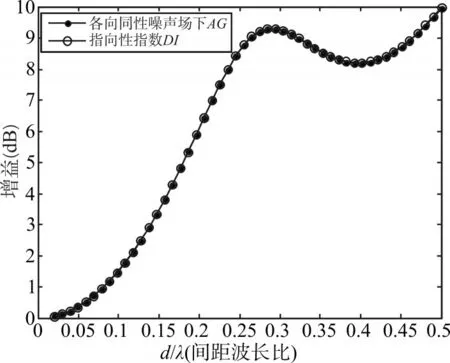
图8 10元圆环阵DI与AG随d/λ的变化
由图6、图7、图8可以看到,在各向同性均匀噪声场下,阵增益与指向性指数完全一致。阵增益随着间距d增大而增大,并在半波长时达到最大值10logN,这与预期值也是吻合的,证明了以上推导的正确性。
4.2 不同束控方向下的阵增益
需要注意的一点是,声纳基阵在进行波束形成时,在不同束控方向其指向性图会发生畸变,因而增益也会发生相应变化,即在不同方向上阵增益是不同的。下面通过对这三种常见阵型的仿真,研究阵增益随束控角度的变化。
1)10元均匀线阵
水平束控90°,垂直方向改变束控角度。用指向性指数DI=10lgRθ表示如表1。
由表1看到当时,线阵的指向性因数DI=10logN。从横向角度来看,阵元间距越大,波束宽度越窄,阵增益增大(“端射”半波长时出现栅瓣故DI减小);从纵向角度来看,从“端射”到“旁射”阵增益递减[11~12],这是由空间投影引起的全空间阵增益变化引起的。
表1 10元均匀线阵指向性指数DI与θ0和关系
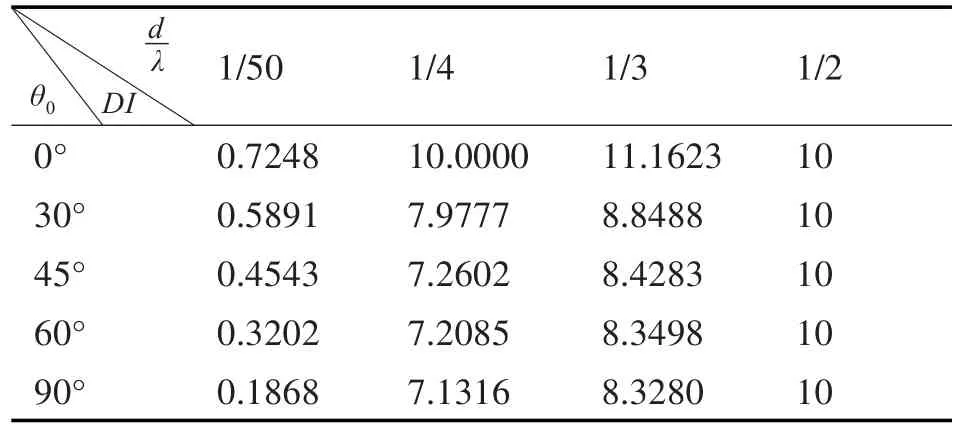
表1 10元均匀线阵指向性指数DI与θ0和关系
dλ θ0DI 0°30°45°60°90°1/50 0.7248 0.5891 0.4543 0.3202 0.1868 1/4 10.0000 7.9777 7.2602 7.2085 7.1316 1/3 11.1623 8.8488 8.4283 8.3498 8.3280 1/2 10 10 10 10 10
2)三元阵
水平束控90°,垂直方向改变束控角度。用指向性指数DI=10lgRθ表示如表2。
表2 三元阵指向性指数DI与θ0和关系
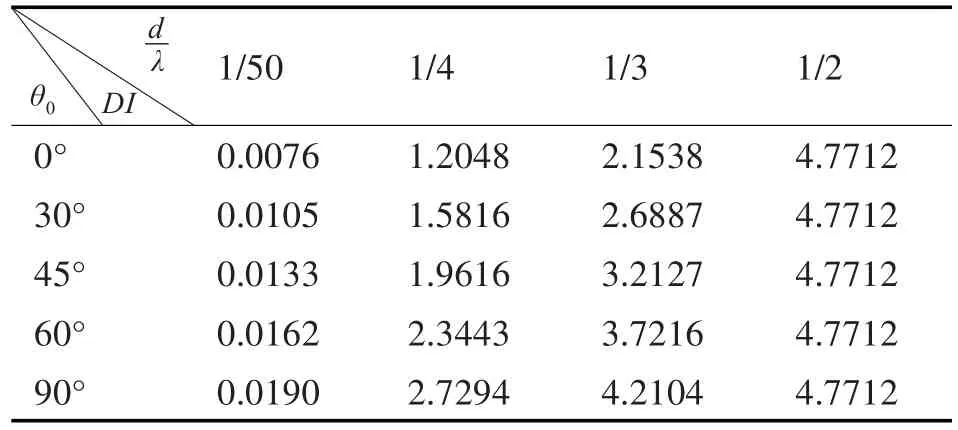
表2 三元阵指向性指数DI与θ0和关系
dλ θ0DI 0°30°45°60°90°1/50 0.0076 0.0105 0.0133 0.0162 0.0190 1/4 1.2048 1.5816 1.9616 2.3443 2.7294 1/3 2.1538 2.6887 3.2127 3.7216 4.2104 1/2 4.7712 4.7712 4.7712 4.7712 4.7712
由表2看到当时,线阵的指向性因数DI=10logN。从横向角度来看,阵增益随阵元间距增大而增大,这是由波束宽度变窄引起的;从纵向角度来看,从0°~90°方向,阵增益递增。
3)圆环阵
水平束控90°,垂直方向改变束控角度。用指向性指数DI=10lgRθ表示如表3。
表3 圆环阵指向性指数DI与θ0和关系
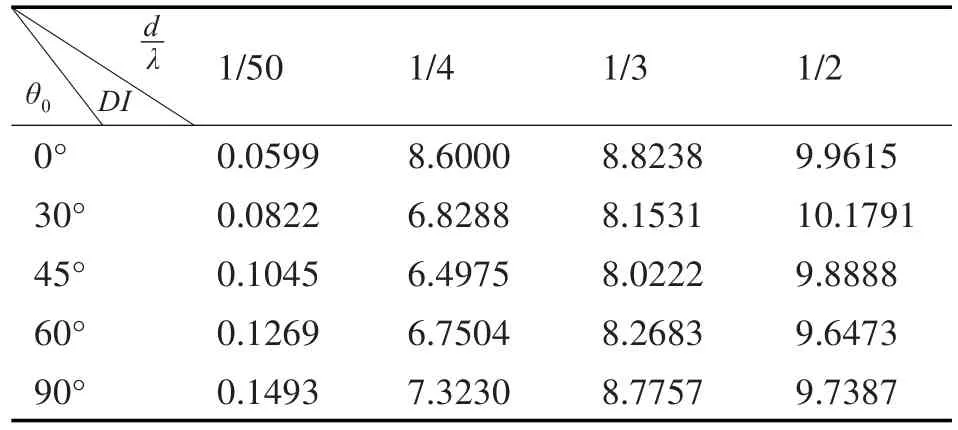
表3 圆环阵指向性指数DI与θ0和关系
dλ θ0DI 0°30°45°60°90°1/50 0.0599 0.0822 0.1045 0.1269 0.1493 1/4 8.6000 6.8288 6.4975 6.7504 7.3230 1/3 8.8238 8.1531 8.0222 8.2683 8.7757 1/2 9.9615 10.1791 9.8888 9.6473 9.7387
从横向来看,同一角度下,阵增益随阵元间距增大而增大,这是由波束宽度变窄引起的;从纵向角度来看,不同角度同一间距时,阵增益呈现不同的空间特性,因而阵增益无明显递增递减规律,这也证明了不同目标角度下基阵所表现的增益能力差异性是比较大的。
5 结语
阵增益是描述系统对信号增强、对噪声抑制能力的量,表现为系统的信噪比增益。常规波束形成下,系统对噪声的抑制能力主要由噪声性质决定。对空间不相关的高斯白噪声10logNdB;对各向同性均匀噪声,阵增益随束控方向而改变,同一角度下,阵增益随阵元间距增大而增大。对均匀线阵,“端射”方向的阵增益大于“旁射”方向。
指向性指数DI是阵增益的一种特殊情况,它是在各向同性均匀同频噪声场下的阵增益。指向性指数DI可由指向性函数或空间波束图计算得,易于仿真计算,而阵增益适用范围广,更具工程意义,但受实际噪声场影响大,不便于计算。对几种常见的阵型进行计算后发现,各向同性均匀同频噪声场下的阵增益与指向性指数DI完全吻合。这为今后前期计算阵增益提供了理论依据,即可由仿真计算得DI估算实际各向同性噪声场下的阵增益,具备实际工程价值。
参考文献
[1]杜功焕,朱哲民,龚秀芬.声学基础[M].南京:南京大学出版社,2001:333-340.
[2]田坦.声纳技术[M].哈尔滨:哈尔滨工程大学出版社,2000:67-121.
[3]李启虎.数字式声纳设计原理[M].安徽教育出版社,2002:179-210.
[4]李启虎.数字式声纳设计原理[M].安徽教育出版社,20黄益旺,杨士莪,朴胜春.体积噪声矢量场空间相关特性研究的一种方法[J].哈尔滨工程大学学报,2009,30(11):1209-1212.
[5]Kleinberg L I.Array gain for signals and noise having am⁃plitudeand phase fluctuations[J].J.Acoust.Soc.Am,1980,67(2):572-577.
[6]张清泉,吉安平,行小帅,李莎莎.基于MATLAB的均匀N元直线阵性能仿真分析.山西师范大学学报[J],2011,25(4):50-53.
[7]杜鹏,李玲,刘彦森,杨学猛.畸变直线阵阵增益计算及仿真研究[J]. 声学技术,2015(4):312-316.
[8]何云峰,等.舷侧阵CBF和OBF的阵增益比较[J].海洋技术,2011,30(3):64-67.
[9]吴碧,王华奎,汪新.实现最佳左右舷分辨的三线阵最佳阵元间距研究[J]. 声学技术,2009(6):803-806.
[10]鄢社锋,马远良.圆环形声基阵低频超增益性能研究[J].西北工业大学学报,2002,20(1):79-82.
[11]Malcolm Hawkes,Member,IEEE and Arye Nehorai,Fellow,IEEE.Acoustic Vector-Sensor Correlations in Ambient Noise[J].IEEE Journal of Oceanic Engineer⁃ing,2001,26(3):337-347.
[12]Richard J Nielsen.Array gain,correlation coefficients,and patchsize[J].J.Acoust.Soc.Am,1977,61(1):60-64.
