基于ADMAS串联机器人运动学仿真与分析评价

周 欣

(西安航空学院 机械工程学院， 陕西 西安 710077)

0 引言

在数字工业化快速发展的时代，机器人作为典型的机电一体化装备的代表，支撑和引领着信息化社会的新兴产业.工业机器人发展成熟，应用范围广，技术不断创新发展，使得机器人在各个行业领域迅速发展.其中串联机器人不但在传统机加工作业中广泛应用，而且在精密，装配，检验等作业中快速发展[1,2].

针对串联机器人的运动学求解，牛顿-欧拉法、拉格朗日法、凯恩法等是研究机器人动力学的经典方法.很多学者进行过深入研究，楼健人，马文建等[3,4]重点分析了解析解法、赵灵宣等[5]分析了几何解法、Mitchell M．Tseng等[6]分析了迭代法、符号求解法及数值方法.但析解法对科研设计人员要求较高，计算量巨大，耗时费力，并且求解条件较理想化，在实际生产中均较难实现.另外，在机器人编程和轨迹规划中，由于应用解析解都会求出多组解，还要再从中求出最优解.针对上述问题，科研人员也逐步使用动力学仿真分析技术进行分析研究，比如应用ADAMS软件在机器人最大载荷的附近仿真空间的跟踪轨迹[5]；应用MATLAB软件对简化后的模型进行动力学分析与仿真[6].

本文以PUMA560串联机器人为例，建立空间坐标系，对串联机器人进行关节结构分析，使用拉格朗日分析法进行运动学分析.根据影响系数理论，建立了一种运动评价方法，引入速度及加速度性能指标，用范数评价位姿精度，为运动性能评价提供一种理论基础.根据ADAMS求解串联机器人运动轨迹与运动物理参量，分析讨论机器人执行机构的运动特性.为机器人运动精度、噪声振动分析及故障诊断等进一步深入研究打下理论基础.

1 串联机器人结构与坐标系

PUMA560是美国Unimation公司早期生产的6自由度串联结构的机器人，是一种经典的、常用的、串联式的工业机器人，属于多关节旋转式的机器人，以此为模型，常用在焊接、装配、搬运等工业生产中.以PUMA560为研究对象，分析工业用串联机器人，整体结构包括基座、腰部、大臂、小臂、腕部等.机器人的腰部和大臂通过腰关节连接，大臂绕着肩关节实现旋转，大臂和小臂通过肘关节连接，带动小臂旋转，通过腕关节，将运动传递给最终的执行机构，从而实现末端机械手的灵活操作，完成装配、搬运等.

分析研究六自由度串联机器人运动特性，串联机器人由6个转动关节带动6个连杆组成，其中3个关节用来确定空间位置，另外3个关节用来确定空间姿态[7].根据D-H法则，指定各个连杆坐标系，其中旋转关节zi轴沿各关节轴向，旋转方向依据右手定则确定，xi指向下一个关节的方向，建立串联机器人连杆坐标系[8]如图1所示.

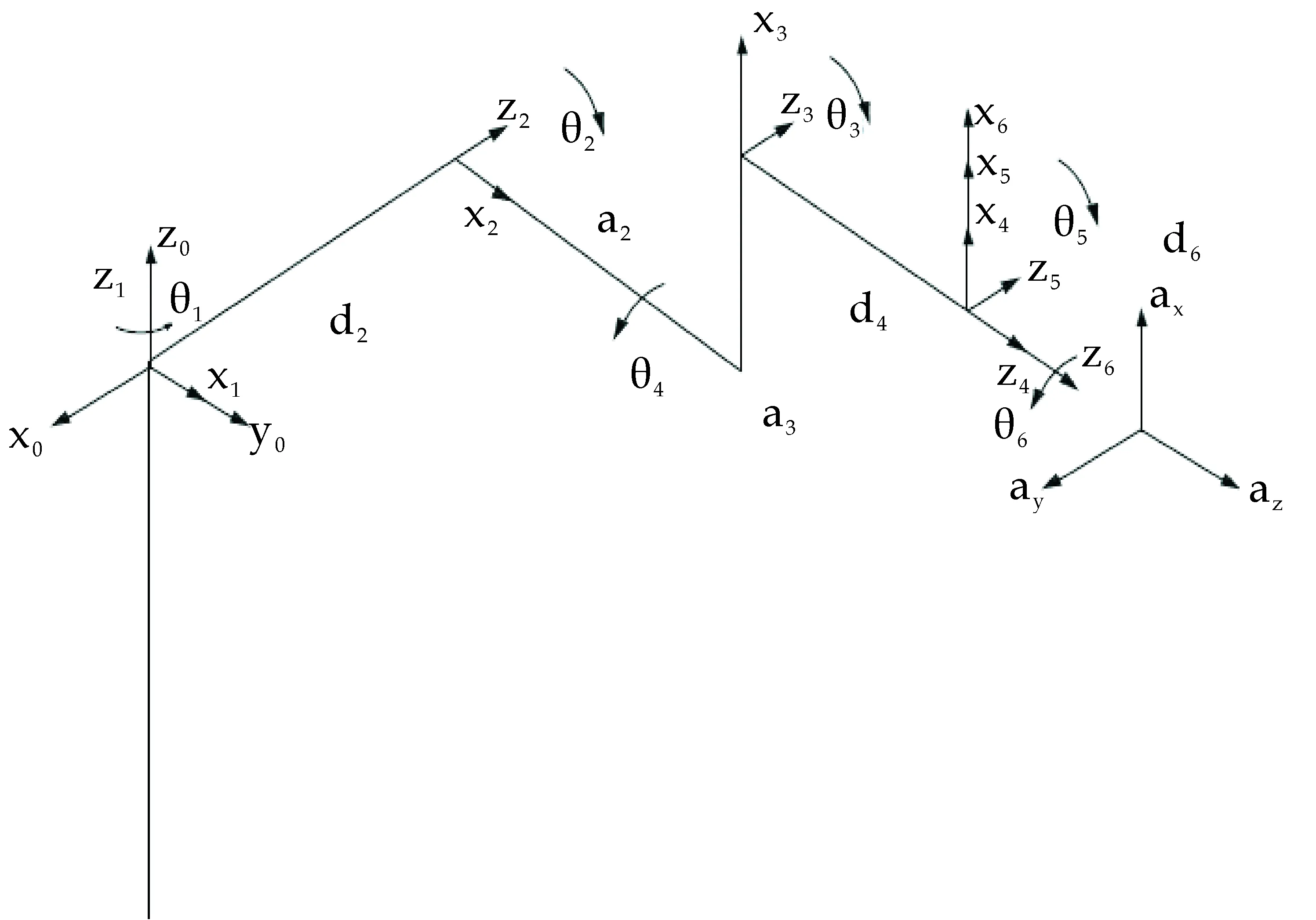
图1 PUMA560机器人连杆坐标系

其中串联机器人的底座和腰构成转动关节1(JOINT_1)，腰和大臂构成转动关节2(JOINT_2)，大臂和小臂构成关节3(JOINT_3)，小臂和手腕1构成转动关节4(JOINT_4)，手腕1和手腕2构成转动关节5(JOINT_5)，手腕2和手腕3构成转动关节6(JOINT_6).

利用UG三维建模软件建立串联机器人模型时，根据研究重点，简化模型，体现串联机器人结构特点即可.忽略不影响传动性能的圆角、倒角等细节特征，从而提高计算效率.根据上述串联机器人结构尺寸参数，建立手臂关节模型，完成虚拟装配.在UG环境下，检查装配质量，经过静态干涉检测，检验零部件的功能性需求.经过动态干涉检测，检验各零部件之间装配干涉以及合理性需求.经过虚拟装配，最终得到串联机器人模型如图2所示.

图2 PUMA560机器人虚拟样机模型

2 串联机器人动力学分析

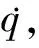
q=[θ1θ2θ3θ4θ5θ6]T

(1)

T=[T1T2T3T4T5T6]T

(2)

(3)

(4)

(5)

(6)

式(6)中：Uij、Uik是变换矩阵关于关节转动角度的导数；Ji、Ii是伪惯量矩阵和驱动器转动惯量.

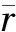
(7)

应用拉格朗日方程L=K-P最终得

(8)

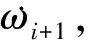
i+1ωi+1×(i+1ωi+1×i+1rCi+1)

(11)

(13)

(15)

τi=iniT·izi

(16)

3 串联机器人运动性能评价指标

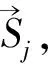
(17)

1≤m≤n≤6

(18)

速度矢量VH，加速度矢量AH如下：

(19)

AH=[εh…ap]T

(20)

速度性能指标分析，υ是各杆件的输出速度组合矢量，定义串联机器人连杆速度性能指标为KG,‖G‖为矩阵G的范数.

(21)

KG=‖G‖‖G-1‖

(22)

加速度性能指标分析，a是各杆件的输出速度组合矢量， 定义串联机器人连杆速度性能指标为KH.

(23)

(24)

4 ADAMS运动仿真分析

根据实验要求，将UG建立的三维模型，导入ADMAS软件，进行动力学仿真.串联机器人大臂a2长度为400 mm，小臂d4长度为420 mm.腕部长度d6为55mm，腰部d2长度为150 mm.

ADAMS软件设置仿真设置持续时间9 s，步数为1 000步.定义机器人逐步的进行阶跃式运动，调用ADAMS阶跃驱动函数STEP(x,Begin At,Initial Function Value,End At,Final Function Value)，对各个关节分别定义如表1所示.

表1 串联机器人各个关节阶跃驱动函数定义

运动仿真结束后，通过ADAMS后处理模块，通过调用模块ADAMS/PostProcessor实现独立后处理，通过回放仿真结果，并对结果进行进一步分析并绘制曲线，完成数学和统计计算，真实反映虚拟样机的特性.对6自由度串联机器人进行分析，可得到各个部件位移、速度、加速度图像如图3所示；各关节力与力矩图像如图4所示.

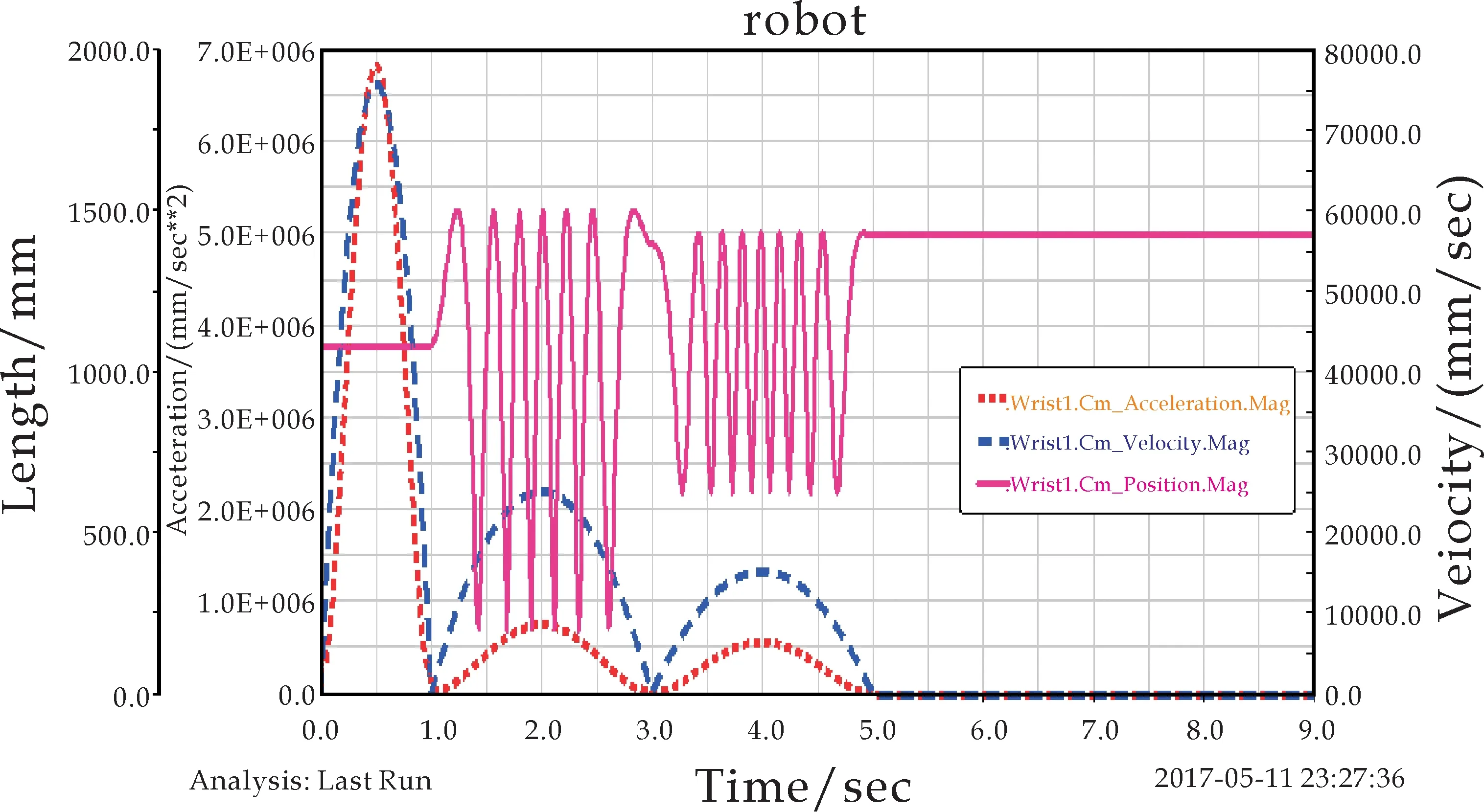
(a)手腕1运动曲线

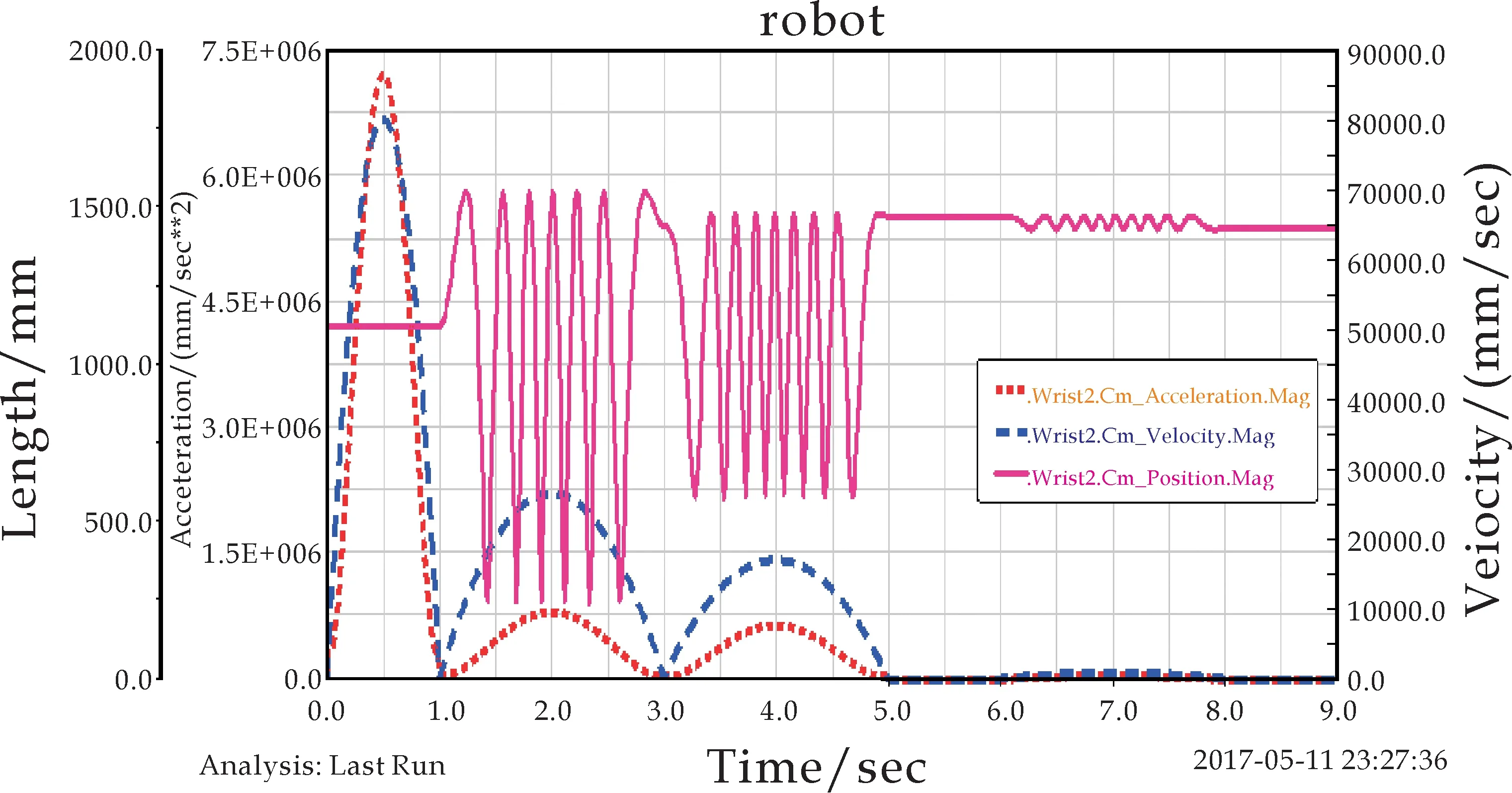
(b)手腕2运动曲线

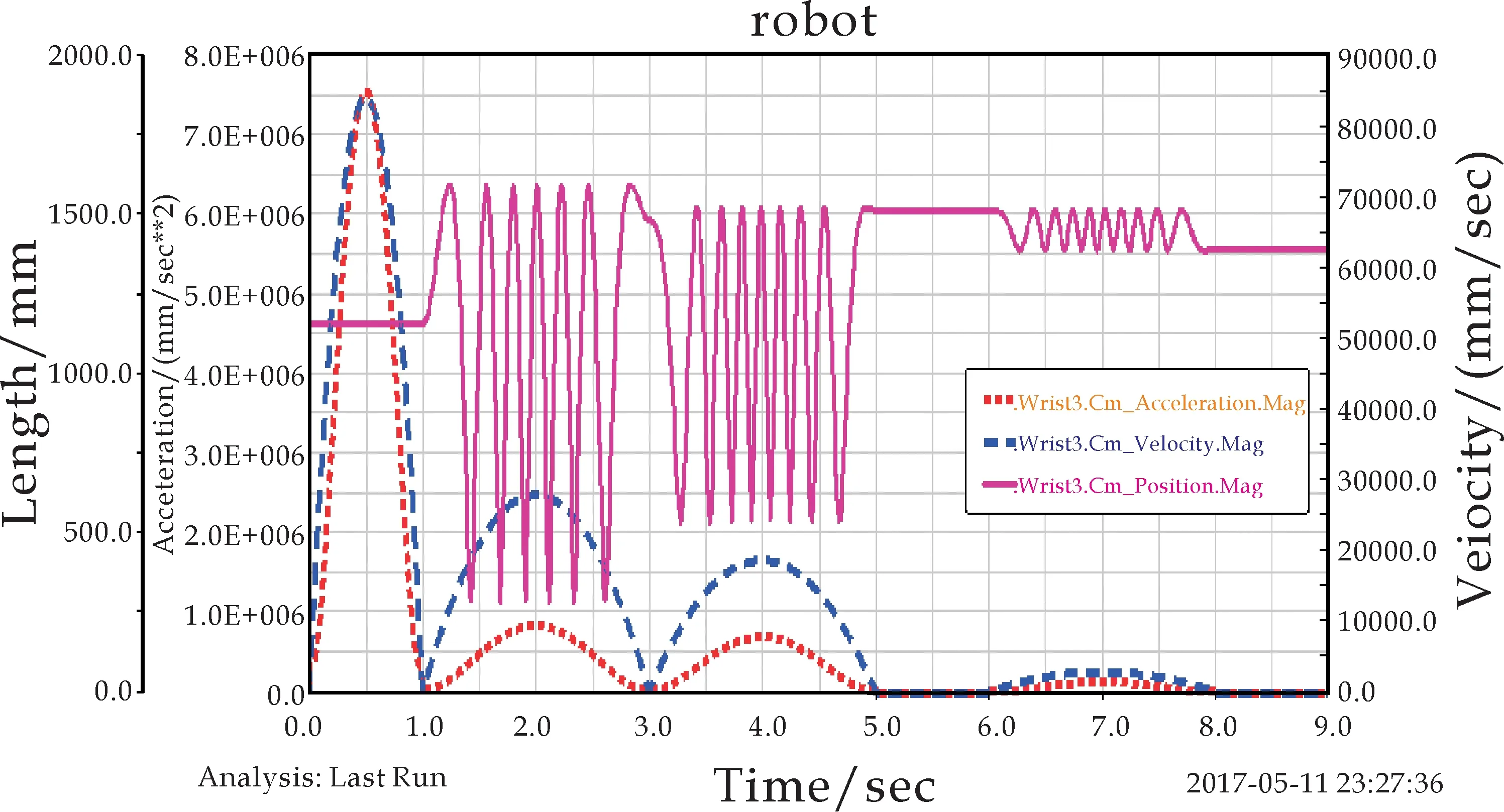
(c)手腕3运动曲线

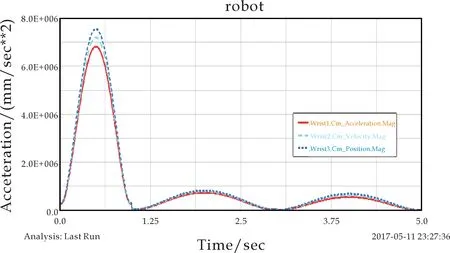
(d)手腕1、2、3加速度曲线

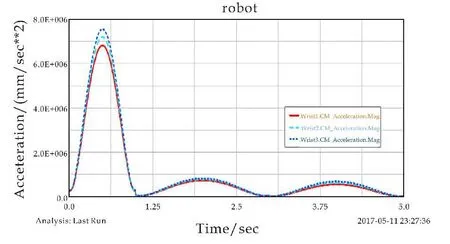
(e)小臂运动曲线

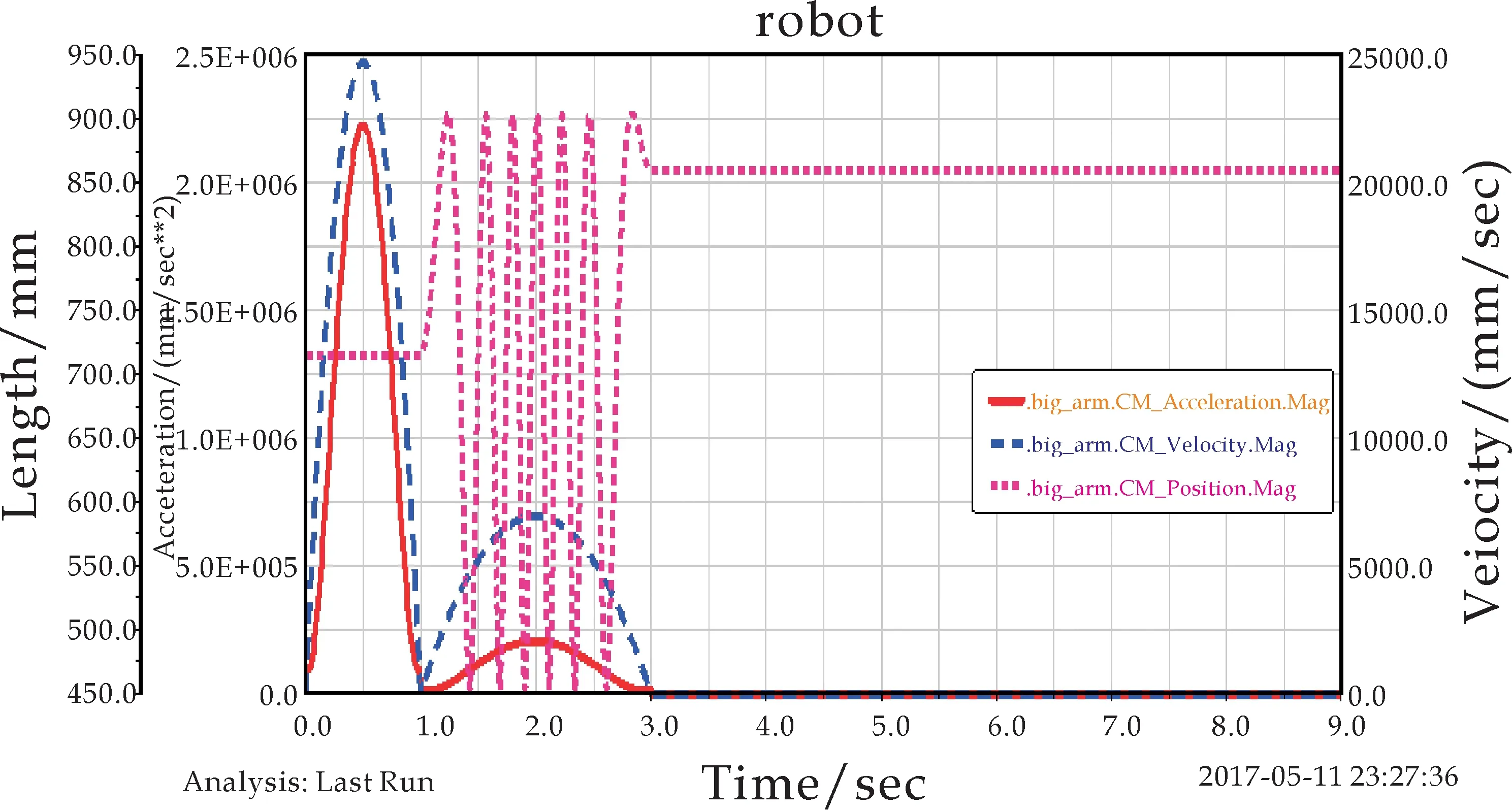
(f)大臂运动曲线图3 串联机器人运动学仿真图像

分析手腕仿真曲线(如图3所示)，可以得到如下结论：三个手腕的速度、位移和加速度三者(a),(b),(c)图像基本相同，但有细微差别.由三个手腕的加速度曲线可得如下结论：在5秒以内，三个手腕加速度图像均产生明显的大幅度振动，在5秒后迅速趋于稳定，8秒后稳定在恒值.并且手腕3的振动幅度明显比手腕2和手腕1大.由此表明，越靠近执行机构末端，手腕的稳定性越差.机器人在执行工作命令时，摆动过程中手臂均会产生小范围抖动，会对执行机构的位置精度造成误差.但在5秒后，机器人末端开始工作时，手腕基本稳定.表明该机器人工作时具有较好的稳定性，同时也验证了运动仿真合理有效.

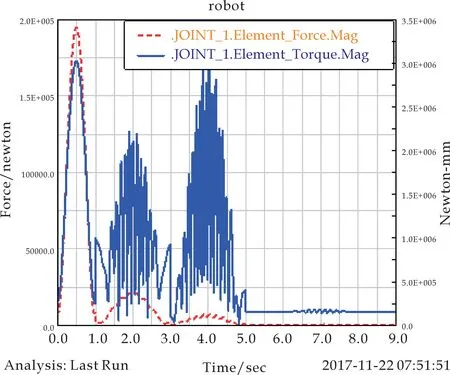
(a)关节1力与力矩曲线

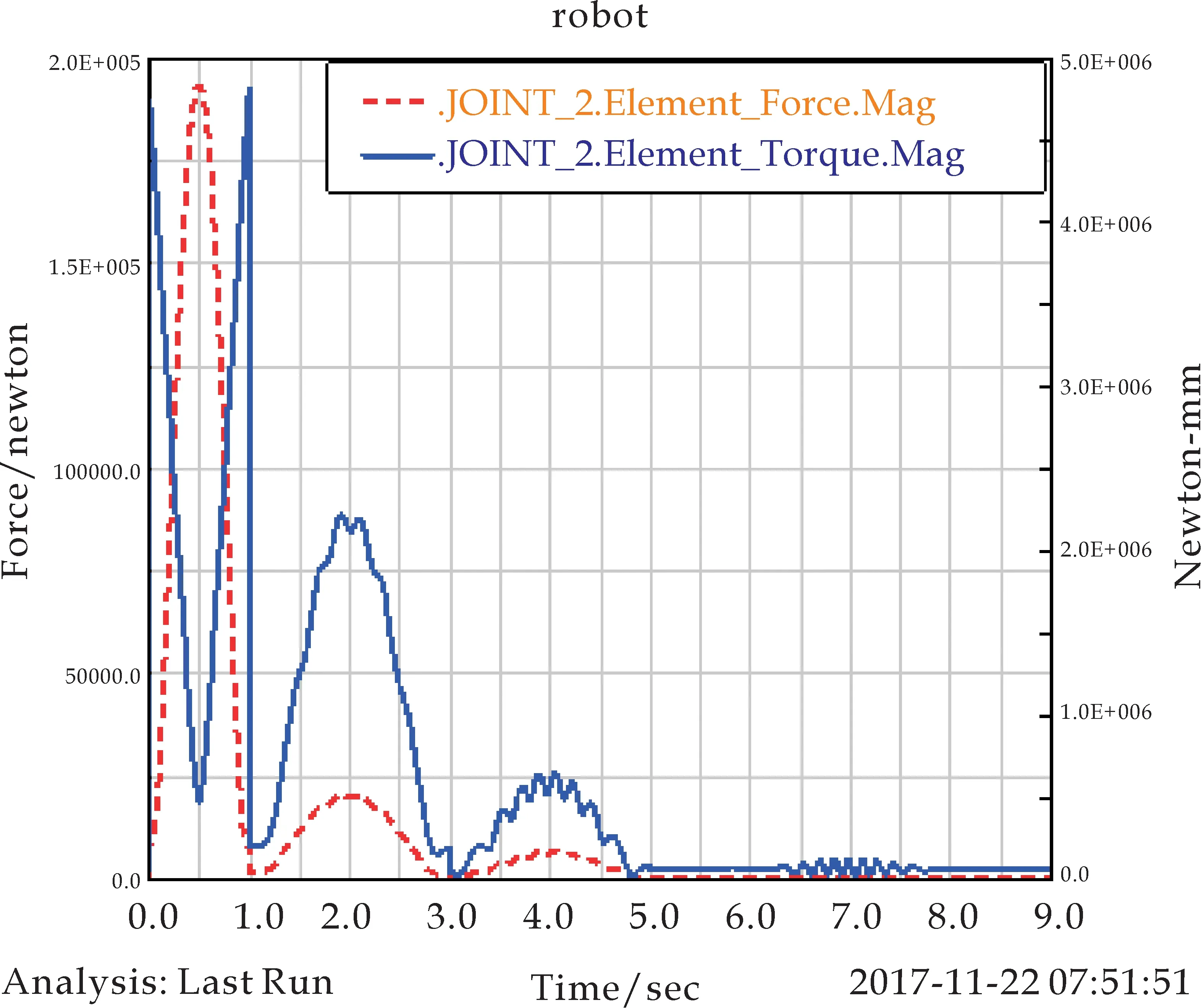
(b)关节2力与力矩曲线

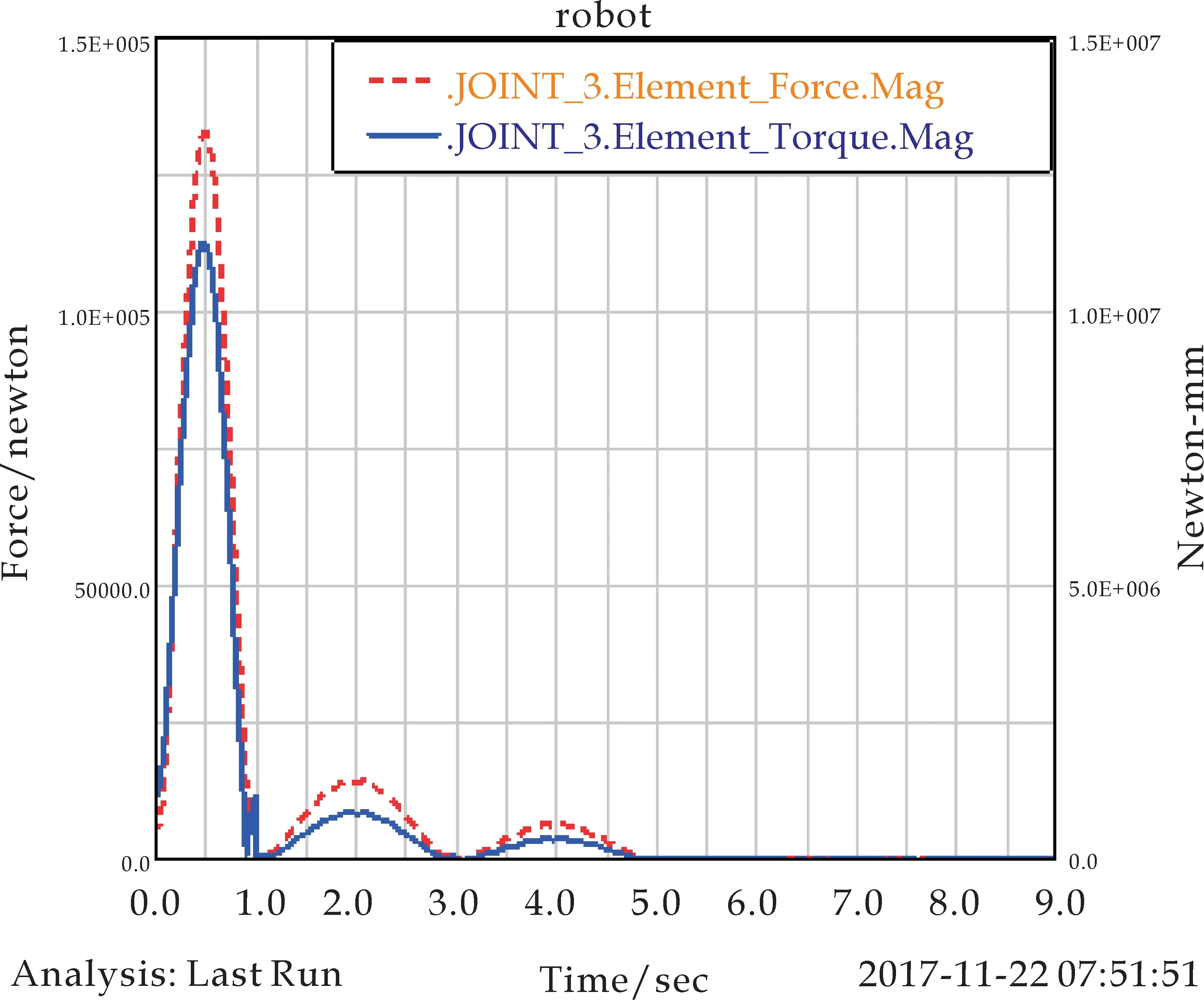
(c)关节3力与力矩曲线

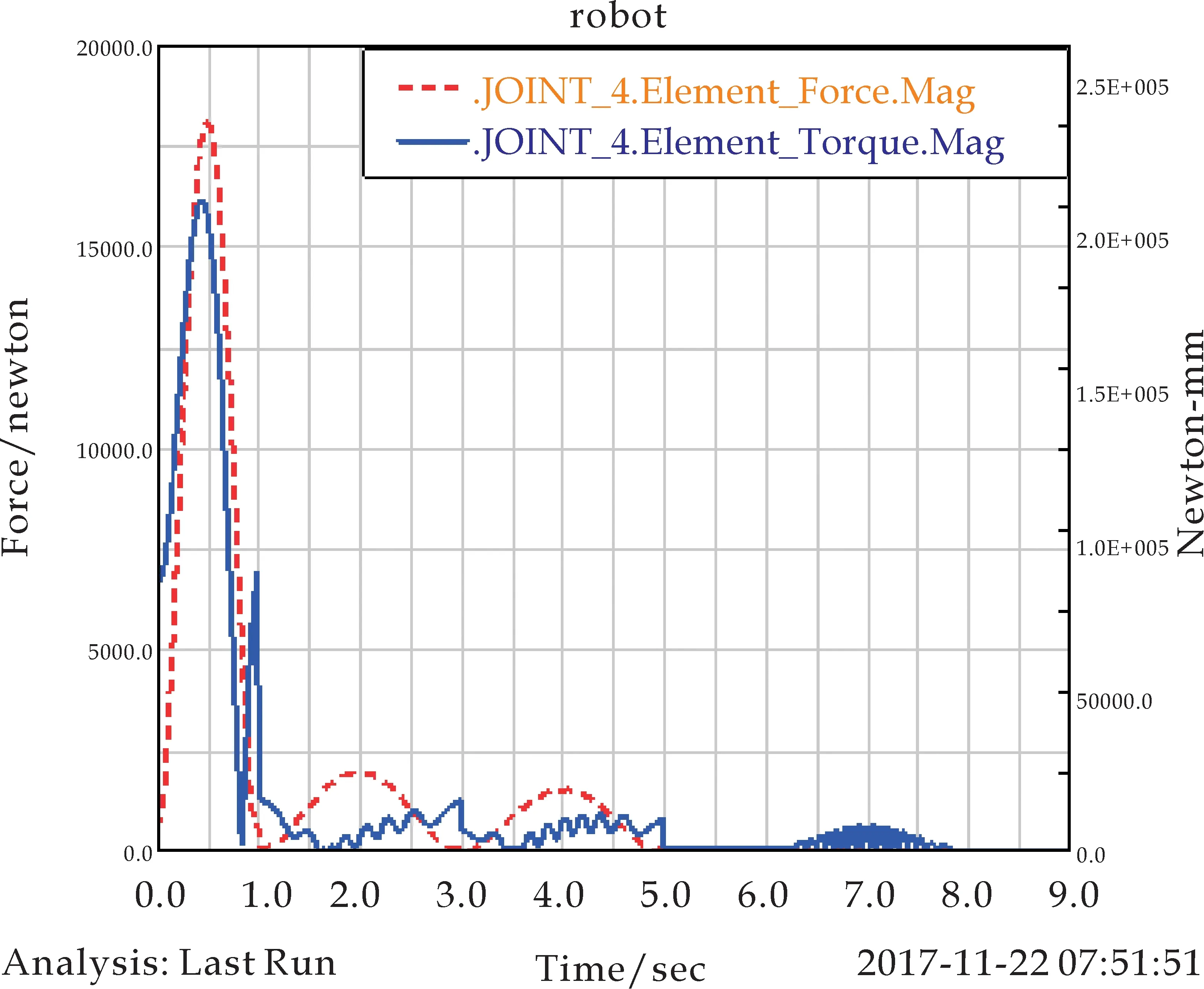
(d)关节4力与力矩曲线

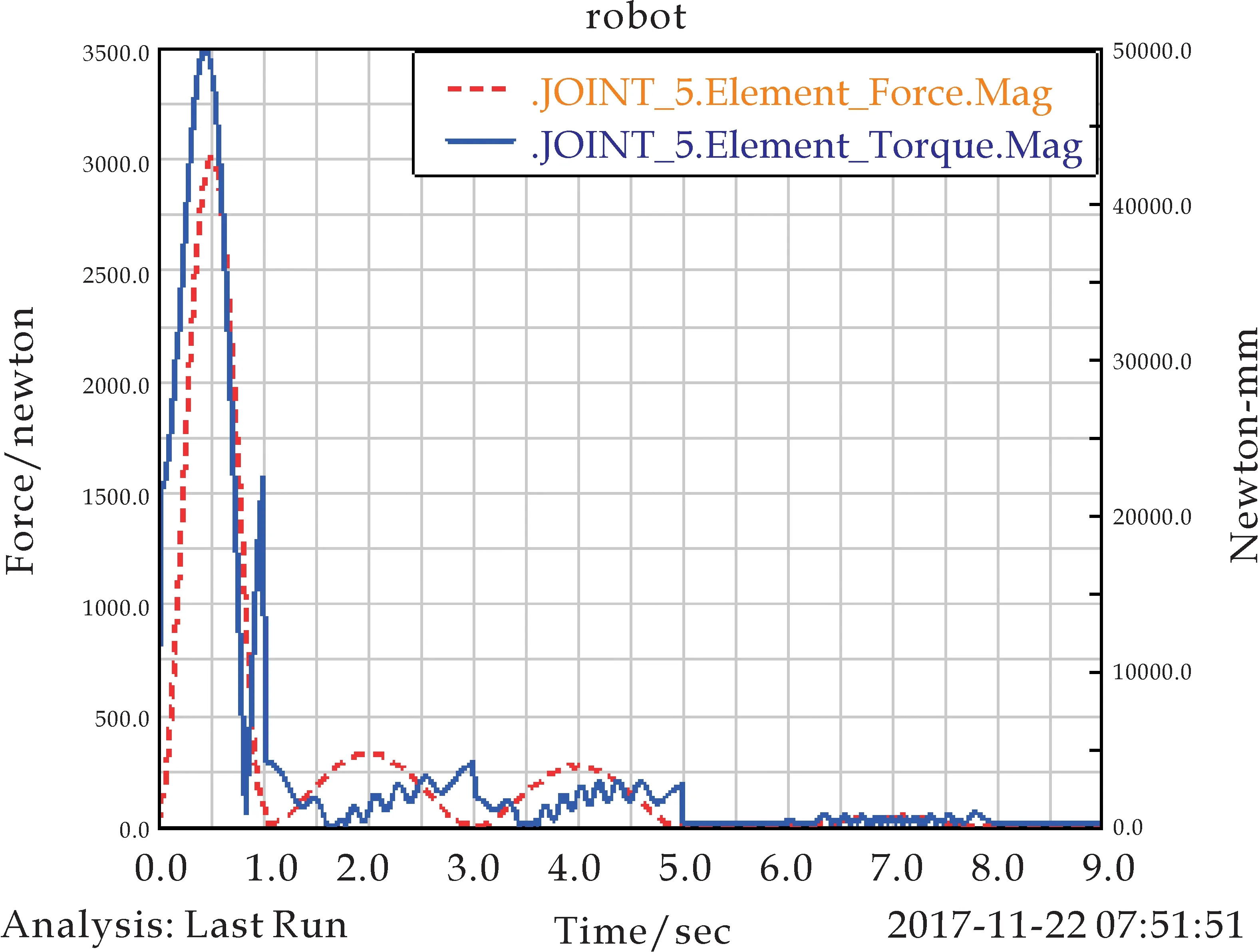
(e)关节5力与力矩曲线

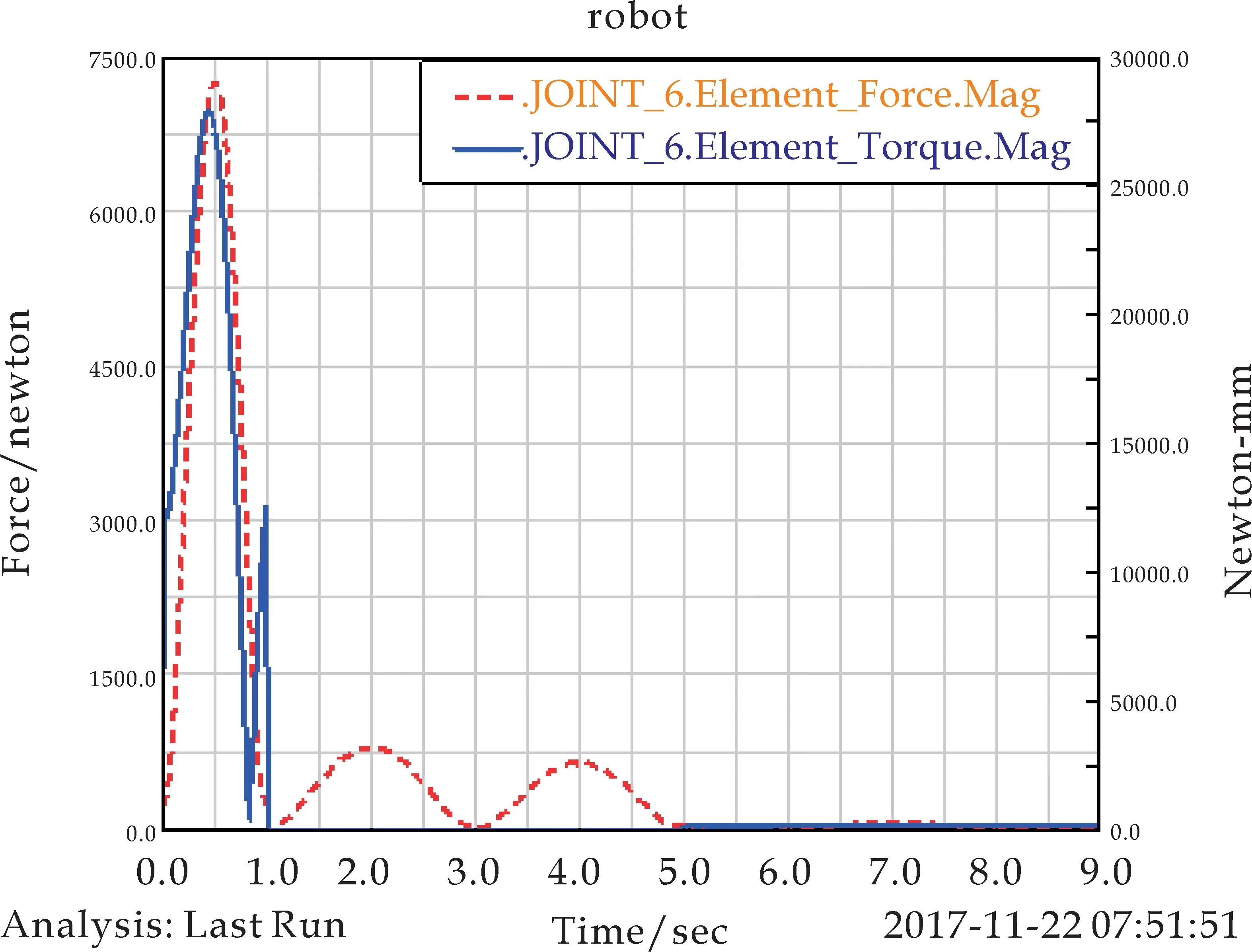
(f)关节6力与力矩曲线图4 串联机器人力学仿真图像

分析手臂仿真曲线(如图3所示)，可以得到如下结论：在1秒内，大臂和小臂加速度达到峰值后逐步衰减至0，并且小臂加速度峰值较大.虽然在1秒内，只有腰部相对基座产生转动，小臂和大臂均为产生相对转动，但远离腰部的小臂加速度相对较大，符合实际.1秒到3秒内，大臂与小臂均出现相同波形和振动.3秒后大臂稳定，表明只有小臂运动时，大臂与基座的稳定性较好.由于模型装配是理想装配，没有带入装配间隙和制造误差，曲线平滑过渡，而没有产生剧烈波动.同时发现为了降低机器人执行机构的振动与误差，提高关节的装配精度与关节控制的稳定性，显得尤为重要.

分析关节仿真曲线(如图4所示)，可以得到如下结论： 6个关节均受到类似正弦规律的力的作用，关节作用力在1秒内迅速上升，并在0.5秒时达到峰值后开始衰减至0.关节在1到3秒，3到5秒均会产生明显的作用力.并且关节1和关节2作用力的曲线会产生小幅度锯齿状振动，其余关节作用力曲线较光滑.另外关节1和关节2在5秒内力矩曲线会产生大幅度振动.表明机器人工作时，与基座连接的关节稳定性相对较差，远端执行机构的稳定性相对较好，满足执行机构工作时的稳定性，符合设计需要.

根据三维模型，利用ADMAS进行运动仿真分析，清晰精确的得到构件的运动规律，符合阶跃驱动函数STEP对于各个关节的驱动函数定义，仿真图像与理论和实际运动状态吻合.有效证明了ADMAS运动仿真是保证结果重要有效步骤.借助仿真软件求解可以大大简化求解过程，方便研究人员进行开发设计，同时也可以辅助高校教师对机器人相关专业进行理论教学工作.

4 结论

本文对六自由度工业串联机器人进行运动学研究和运动性能评价.本文以PUMA560串联机器人为例，进行运动学分析.运用空间坐标系，采用拉格朗日法对串联机器人进行动力学研究.利用影响系数理论分析运动性能评价指标，推导出速度和加速度性能评价指标，为运动性能评价提供一种理论基础.利用UG建立机器人三维模型，装配虚拟样机，利用ADMAS动力学软件，求解串联机器人运动轨迹与运动物理参量，简化运算过程，提高工作效率.

[1] 李增刚.ADAMS入门详解与实例[M].北京：国防工业出版社,2010.

[2] 刘义翔,李瑞峰,李东婉.应用ADAMS软件对点焊机器人大臂机构进行动力学仿真研究[J].哈尔滨商业大学学报(自然科学版),2001,17(3)：63-66.

[3] 楼健人,张树有,谭建荣,等．面向 DFMC 的产品配置设计技术研究[J].中国机械工程, 2004,15(1)：42-44,49.

[4] 马文建,刘 伟,李传昭.并行产品开发中设计活动间重叠与信息交流[J].计算机集成制造系统,2008,14(4)：630-636.

[5] 赵灵宣,檀润华,张换高,等.基于产品平台的产品配置方法研究[J].机械设计与制造, 2008(6)：213-215.

[6] Jianxin Jiao,Mitchell M.Tseng.Customizability analysis indesign for mass customization[J].Computer-Aided Design,2004(36)： 745-757.

[7] 邢葆轶.基于 QNX 的七自由度机械臂控制系统设计[D].沈阳: 沈阳理工大学,2013.

[8] 孙志礼,姬广振.机构运动可靠性设计与分析技术[M].北京：国防工业出版社,2015：80-125.

[9] 王殿君,关似玉,陈 亚,等.六自由度搬运机器人动力学分析及仿真[J].机械设计与制造,2017(1):25-29.

[10] 崔敏其.SCARA 机器人的拉格朗日动力学建模[J].机械设计与制造,2013(12)：76-78.

[11] 蔡自兴.机器人学[M].北京:清华大学出版社,2009:122-125.

[12] 罗建国,何茂艳,陆 震,等.基于UG的串并联机器人ADAMS运动学仿真[J].机械设计,2007,24(4):5- 8.

[13] Herman P.On using generalized velocity components for manipulator dynamics and control[J].Mechanics Research Communications，2006,33(3):281-291.

[14] 李庆龄,赵永生.六自由度工业机器人动力学分析与仿真[J].上海电机学院学报,2008,11(4):275-278.

[15] 魏 武,袁银龙,王新梅. 基于影响系数原理的六足机器人运动状态分析[J].系统工程与电子技术,2016,38(2):375-381.

[16] 朱鑫翔,许德章.基于运动学性能的串联机器人评价矩阵的建立及分析[J].蚌埠学院学报,2017,6(4):21-30.