C(PF′)系对幺半群的刻画

梁星亮， 袁海龙， 柏 茜

(陕西科技大学 文理学院， 陕西 西安 710021)

0 引言

半群代数理论作为代数学的重要组成部分， 在信息科学、自动机理论、图论、离散数学、密码学等学科中有着重要而又广泛的应用[1].而半群S-系作为半群的一种表示理论，是研究半群代数结构的有力工具，其主要思想是利用半群的右S-系范畴的性质去刻画半群的结构，已有许多重要的研究成果面世[2-11].目前，关于S-系范畴中的投射性和内射性的研究成果已非常丰富[2]，但是对于正则性，只有少数研究成果出现[3,4].因此，本文将继续致力于正则性质的研究.

文献[3]和[4]中分别介绍和研究了正则系的推广，即CSF系和C(P)系.称右S-系A是CSF系[3]，如果A的所有循环子系是强平坦的.称右S-系A是C(P)系[4]，如果A的所有循环子系满足条件(P).由文献[3]知，CSF系是正则系的一个真推广，且利用CSF系刻画了PSF幺半群.所谓PSF幺半群是指S的每一个主右理想作为右S-系是强平坦的.因为条件(PF′)是S-系范畴中一个重要的平坦性质，又是强平坦性的一个重要推广，所以很自然地考虑A的所有循环子系满足条件(PF′)的幺半群类的结构特征.

本文的主要目的是研究一类比CSF系更广的正则系的推广-C(PF′)系.通过S-系的C(PF′)性质，刻画了一些新的幺半群的结构，推广了已有重要的结果.本研究可以深化S-系理论在半群中的应用，对于揭示S-系理论与模理论的区别与联系，探索平坦性质在S-系中的应用具有重要意义.

方便起见，首先给出本文所用到的一些基本概念.本文假设S是幺半群，1是其单位元，E(S) 表示S的所有幂等元的集合，N表示自然数的集合.

设A是非空集合.若存在映射

f:A×S→A，(a,s) |→as，

满足

(as)t=a(st)和a·1=a,∀s,t∈S,∀a∈A，

则称是一个右S-系，或称S右作用于A，通常简记为AS.类似地，可以定义左S-系SA.

设A，B都是右S-系.称映射f为从A到B的S-同态，如果

f(as)=f(a)s,∀s∈S,∀a∈A.

所有右S-系以及右S-系之间的同态构成一个范畴，称之为右S-系范畴，记为Act-S.

设A是右S-系.称元素a∈A是半可消的[3]，如果对任意s,t∈S，若as=at，存在r∈S使得rs=rt，且a=ar.

1 C(PF′)系

本节首先引入C(PF′)系的概念，并给出它的一些基本性质.

定义1称一个右S-系A是C(PF′)系，如果A的所有循环子系满足条件(PF′).

定义2称一个幺半群S是右P(PF′)的，如果S的每一个主右理想作为右S-系满足条件(PF′).

注1因为强平坦⟹ 条件(PF′)⟹条件(P)，所以CSF⟹C(PF′)⟹C(P).文献[4]中例子可以证明第二个递推关系是严格的.下面例1说明了第一个递推关系也是严格的.

例1设S={1,-1} ，其上的运算为数乘.显然S是一个非平凡群.现在我们考虑一元S-系ΘS={θ}.容易验证ΘS是一个C(PF′)系.但ΘS不是CSF系，这是因为θ·1=θ·(-1)，但是不存在r∈S，满足r·1=r·(-1).因此，C(PF′)系是CSF系的一个真推广.

文献[3]证明了右S-系A是CSF系当且仅当A的每一个元素是半可消的.受此启发，我们首先给出C(PF′)系的一个结构刻画.

定义3设A是右S-系.称a∈A元素是弱半可消的，如果对任意x,y,s,s′,t,t′,z,w，

axs=ays′sz=tw,

axt=ayt′s′z=t′w,

存在p,q∈S，使得

ax=ap,ay=aq,且ps=qs′,pt=qt′.

如果A中每一个元素都是弱半可消的，则称A是弱半可消的.

定理1设S是幺半群,A是右S-系.则下述条件等价:

(a)A是C(PF′)系；

(b)A的每一个循环子系是由A的一个弱半可消元生成；

(c)A的每一个元素是弱半可消元.

证明：(a)⟹(c)假设A是C(PF′)系.则对任意的a∈A，aS满足条件(PF′).若任意的x,y,s,t,z,w∈S满足

axs=ays′,sz=tw

axt=ayt′,s′z=t′w

则存在a″∈aS，u,v∈S，使得ax=a″u，ay=a″v，且us=vs′,ut=vt′.由a″ ∈aS存在m∈S，使得a″ =am，因此有，ax=amu，ay=amv且mus=mvs′,mut=mvt′.从而由定义3知是A的弱半可消元.

(c)⟹(b)显然成立.

(b)⟹(a)任意的a∈A,aS是A的一个循环子系，下证aS满足条件(PF′).由条件(b)知，不妨设a就是弱半可消元.若axs=ays′，axt=ayt′，sz=tz，s′z=t′z,x,y,s,t,z∈S，根据定义3，必存在p,q∈S，使得

ax=ap,ay=aq，且ps=qs′,pt=qt′,这表明aS满足条件(PF′) ，故A是C(PF′)系.

命题1设S是幺半群.所有的C(PF′)系满足条件(E′).

证明：设A是C(PF′)右S-系.若s,s′,z∈S，a∈A，使得as=as′，sz=s′z，则有等式组：

as=as′,sz=1·sz,

a·1=a·1,s′z=1·sz.

因为A是C(PF′)系，所以存在p,q∈S，使得ps=qs′，p·1=q·1且a=ap=aq.故满足条件(E′) .

称幺半群S是右reversible的[6]，如果对任意的s,t∈S，存在p,q∈S，使得ps=qt.称幺半群S是(弱)左collapsible的[6]，如果对任意的s,t,z∈S,(sz=s′z),存在u∈S，使得us=ut.

命题2设S是幺半群.则下述条件等价:

(a)一元S-系ΘS={θ}是C(PF′)的；

(b)S是右reversible的和弱左collapsible的.

证明：(a)⟹(b)由定理1立得.

(b)⟹(a)假设对任意s,s′,t,t′,z，w

θs=θs′，sz=tw,

θt=θt′,s′z=t′w.

因为S是右reversible的幺半群，所以对s和s′存在p,q∈S，使得ps=qs′.从而计算得

qt′w=qs′z=psz=ptw.

再利用S的弱左collapsible性质，存在u∈S，使得upt=uqt′.因此有

θ=θup=θuq,且ups=uqs′,upt=uqt′.

下面命题给出了S-系的余直积保持C(PF′)性质.

命题3设S是幺半群.则以下结论成立：

(a)C(PF′)系的子系仍然是C(PF′)系.

(b)C(PF′)系的余直积仍是C(PF′)系.

证明：(a)由定义容易得证.

命题4设M,N均为右S-系.若单同态f:M→N可收缩，且N是C(PF′)系，则M是C(PF′)系.

证明：任意的a∈M,s,t,s′,t′,x,y,z,w∈S，若

axs=ays′,sz=tw,

axt=ayt′,s′z=t′w

则显然有f(a)xs=f(a)ys′和f(a)xt=f(a)yt′.由条件f(a)∈N，且N是C(PF′)系，根据定理1，必存在p,q∈S，使得

f(a)x=f(a)p,f(a)y=f(a)q，

且ps=qs′，pt=qt′.因为f是可收缩的，所以存在同态g:N→M，使得gf=1M.因此，

ax=gf(a)x=gf(a)p=ap，

同理可得ay=aq，从而命题得证.

本节最后，考虑幺半群S在什么条件下，S-系的直积将C(PF′)性质转移到每一个分量上.

命题5设S是左collapsible幺半群，I是非空集合.若∏i∈IAi是C(PF′)系，则每一个Ai,i∈I,是C(PF′)系.

证明：假设对任意的s,t,s′,t′,x,y,z,w∈S,ai∈Ai，满足

aixs=aiys′,sz=tw

aixt=aiyt′,s′z=t′w.

因为S是左collapsible的，所以对xs和ys′以及xt和yt′存在u,v∈S,使得uxs=uys′和vxt=vyt′.对u和v再利用S的左collapsible性质，存在w∈S,使得wu=wv.因此，wuxs=wuys′和wvxt=wvyt′.任意的j≠i和aj∈Aj，就有

ajwuxs=ajwuys′和ajwvxt=ajwvyt′.

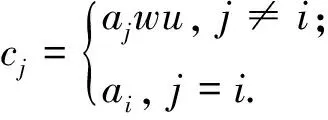
(cj)j∈Ixs=(cj)j∈Iys′, (cj)j∈Ixt=(cj)j∈Iyt′

因为∏i∈IAi是C(PF′)系，所以存在p,q∈S，使得(cj)j∈Ix=(cj)j∈Ip，(cj)j∈Iy=(cj)j∈Iq，且ps=qs′，pt=qt′.因此有aix=aip,aiy=aiq,从而命题得证.

由上述命题的证明，容易获得

推论1设S是幺半群，I是非空集合.若∏IA是C(PF′)系，则A也是C(PF′)系.

2 C(PF′)系对幺半群的刻画

本节主要考虑C(PF′)系对幺半群的刻画.首先给出右C(PF′)幺半群的等价描述，下面的命题可由定理1直接可得.

命题6对于幺半群S，以下条件等价：

(a)S是右C(PF′)的；

(b)S的每一个主右理想由S的一个弱半可消元生成；

(c)S的每一个元素是弱半可消元.

定理2设S是幺半群.则以下条件等价：

(a)S是右P(PF′)幺半群；

(b)所有满足条件(E)的右S-系是C(PF′)系；

(c)所有满足条件(E)的有限生成的右S-系是C(PF′)系；

(d)所有满足条件(E)的循环右S-系是C(PF′)系.

证明：(b)⟹(c)⟹(d)显然.

(d)⟹(a)因为S是满足条件(E)的右S-系，所以由条件(d)知S是C(PF′)系，根据定理1和命题6，S是右C(PF′)幺半群.

(a)⟹(b)假设A是满足条件(E)的右S-系.若对任意的a∈A,s,s′,t,t′,x,y,z,w∈S，满足

axs=ayt′,sz=tw，

axt=ayt′,s′z=t′w，

利用条件(E)的定义，则由等式axs=ays′知，存在a′∈A,u∈S，使得a=a′u，且uxs=uys′.将a=a′u代入到等式axt=ayt′中，得a′uxt=a′uyt′，再利用条件(E)，存在a″∈A,v∈S，使得a′=a″v，vuxt=vuyt′.因此有

vuxs=vuys′,sz=tw，

vuxt=vuyt′,s′z=t′w.

又因为S是右P(PF′)幺半群，所以存在p,q∈S，使得

(vu)x=(vu)p,ps=qs′

(vu)y=(vu)q,pt=qt′.

从而ax=a′ux=a″vux=a″vup=a′up=ap，同理ay=aq.这说明A是C(PF′)系.

定理3设S是幺半群.则下述条件等价：

(a)所有自由的右S-系是C(PF′)系；

(b)所有投射的右S-系是C(PF′)系；

(c)所有强平坦的右S-系是C(PF′)系；

(d)所有强平坦的循环右S-系是C(PF′)系；

(e)S是右P(PF′)幺半群.

证明：(c)⟹(b)⟹(a)和(c)⟹(d)是显然的.

(e)⟹(c)因为S是右P(PF′)幺半群，所以由定理2可知，每一个满足条件(E)的右S-系是C(PF′)系，又因为强平坦系满足条件(E)，所以每一个强平坦的右S-系是C(PF′)的.

(d)⟹(e)因为S是强平坦的循环右S-系，根据条件(d)，S是C(PF′)系，从而由定理1与命题6可知结论成立.

(a)⟹(e)显然S是自由系，故由条件(a)知，S就是C(PF′)系，从而由定理1与命题6即得结论.

下面给出正则幺半群的一些新的刻画，为此，需要下面的结果.

引理1[2]设I是S的真右理想.则右S-系A(I)满足条件(E)，但不满足条件(PWP).

引理2[5]设S是幺半群.则所有满足条件(E′)的右S-系是(主弱)平坦的当且仅当S是正则幺半群.

引理3[5]设S是幺半群.则所有满足条件(E′)的右S-系满足条件(PF′)当且仅当S是群.

定理4设S是幺半群.则下述条件等价:

(a)S是右P(PF′)幺半群，且所有C(PF′)的右S-系是平坦的；

(b)S是右P(PF′)幺半群，且所有C(PF′)的右S-系是弱平坦的；

(c)S是右P(PF′)幺半群，且所有C(PF′)的右S-系是主弱平坦的；

(d)S是正则幺半群.

证明：(a)⟹(b)⟹(c)显然.

(c)⟹(d)任取s∈S，若sS=S，显然s是S中的正则元.否则sS就是S的一个真右理想，由引理1知，A(sS)满足条件(E)，因为S是右P(PF′)幺半群，根据定理2，A(sS)是C(PF′)系，进而由条件(c)知，A(sS)是主弱平坦的.再根据引理2，对于s∈sS，有s∈sSs，这说明了s是S中的正则元.

(d)⟹(a)如果S是正则幺半群，则由[3，定理2.5]和注1知，S是右P(PF′)幺半群.另一方面，根据引理2和命题1，所有C(PF′)的右S-系是平坦的.

定理5设S是幺半群.则下述条件等价:

(a)S是右P(PF′)幺半群，且所有C(PF′)的右S-系满足条件(PF′)；

(b)S是右P(PF′)幺半群，且所有C(PF′)的右S-系满足条件(P)；

(c)S是右P(PF′)幺半群，且所有C(PF′)的右S-系满足条件(WP)；

(d)S是右P(PF′)幺半群，且所有C(PF′)的右S-系满足条件(PWP)；

(e)S是群.

证明：(a)⟹(b)⟹(c)⟹(d)显然.

(d)⟹(e)假设sS是S的一个真的右理想，s∈sS.则由引理1知，A(sS)满足条件(E)，因为S是右P(PF′)幺半群，根据定理2，A(sS)是C(PF′)系，进而由条件(d)知，A(sS)满足条件(PWP).但这与引理1矛盾，故S是群.

(e)⟹(a) 如果S是群，显然S是右P(PF′)幺半群.另一方面，根据引理3和命题1，所有C(PF′)的右S-系满足条件(PF′)，从而定理得证.

3 结论

本文在S-系范畴中引入了C(PF′)性质，由例1可知，C(PF′)性质是S-系中正则性的一种推广形式，它与其它正则形式具有以下严格递推关系：

正则性⟹CSF⟹C(PF′)⟹C(P).

进一步地，利用S-系的C(PF′)性质刻画了P(PF′)幺半群、正则幺半群、群等重要幺半群的结构，推广了CSF系的已有相关重要结果，例如定理1-5.特别地，如果S是含有一个右零元或者是右Collapsible幺半群时，不难验证CWPF系就是CSF系，这与在S-系范畴中条件(PF′)和强平坦性是一致的结论相吻合.

[1] Howie J M.An introduction to semigroup theory[M].London：Academic Press,1976.

[2] 刘仲奎,乔虎生.半群的S-系理论[M].北京: 科学出版社,2008.

[3] Liu Z K.A generalization of regular left acts[J].Northeast.Math.J.,1997,13(2):169-176.

[4] 乔虎生.C(P)系对幺半群的刻画[J].数学研究与评论,2004,24(1):119-126.

[5] Golchin A,Mohammadzadeh H.On homological classification of monoids by condition(E′)of right acts [J].Yokohama Math.J.,2007,54:79-88.

[6] Liang X L,Luo Y F.On a generalization of weak pullback flatness[J].Comm.Algebra,2016,39:3 796-3 817.

[7] Bailey A,Renshaw J.Covers of acts over monoids and pure epimorphisms[J].Proc.Edinb.Math.Soc.,2014,57(3):589-617.

[8] Bulman Fleming S.Pullback flat acts are stongly flat[J].Canad.Math.Bull.,1991,34(4):456-461.

[9] Bulman Fleming S.Flat and strongly flatS-systems[J].Comm.Algebra,1992,20(9):2 553-2 567.

[10] Bulman Fleming S,Kilp M,Laan V.Pullbacks and flatness properties of acts II[J].Comm.Algebra,2001,29(2):851-878.

[11] Laan V.Pullbacks and flatness properties of acts Ⅰ[J].Comm.Algebra,2001,29:829-850.