一类具有控制措施的结核病治疗模型分析

阴奇麟， 曹 慧， 王晓琴

(陕西科技大学 文理学院， 陕西 西安 710021)

0 引言

结核病是由结核杆菌引起的一种古老的慢性传染病，主要经呼吸道传播，它仅次于艾滋病，是全球引起人类死亡的第二大传染病[1].世界卫生组织2017年发布的结核控制报告显示[2]，2016年全球新发结核病例约为1 040万，与结核病相关的死亡人数达130万.我国的结核病疫情也相当严重， 2010年结核病流行病学抽样调查报告显示[3]，2010年我国15岁及以上人群活动性肺结核的患病率为459/10万.因此，结核病的预防和控制一直是国际和国内疾病控制部门和传染病领域关注的热门课题.

借助数学模型对结核病的传播进行理论分析和定量研究已经成为传染病研究的一种重要方法[4-6].通过对数学模型动力学性态的研究可以展示结核病的发展过程，预测其流行规律和发展趋势，分析其流行的原因和关键因素，寻求对其进行控制、预防和治疗的最优策略，为人们制定防治决策提供理论基础和数量依据.相对而言，将优化控制问题应用于分析结核病传播问题的研究还是比较少的[7].2002年开始了利用优化控制探讨结核病传播问题的第一篇文章[7].

最近几年，开始有学者关注结核病传播问题的优化控制模型研究[8-11].文献[8]讨论了一类具有外源再感染的结核病模型，希望通过设置优化控制策略使得感染人数最少；文献[9]在考虑外源再感染的同时也考虑对潜伏感染者进行治疗的结核病模型，实施的优化控制措施是针对潜伏感染者进行治疗使得基本再生数能够降低；文献[10]考虑了一类对结核杆菌感染者进行跟踪治疗的结核病模型，目的是设计优化控制措施来减小一些中途停止治疗并失踪的个体人数；文献[11]主要研究了一类具有再感染和外源再感染的结核病模型，在花费最小的条件下设计了再感染控制策略、外源再感染控制策略.

鉴于非耐药结核病人和耐药结核病人的治愈率中有明显差异，在本文中将染病者划分为非耐药结核病人和耐药结核病人两类，并考虑对染病者进行分类治疗的优化控制结核病模型.

1 具有控制的结核病模型

将整个人群划分为易感者、潜伏感染者和染病者三类，并且分别用S(t)，E(t)和I(t)表示t时刻易感者、潜伏感染者和染病者类中的个体数量.用N(t)表示t时刻的总人口数，满足N(t)=S(t)+E(t)+I(t).

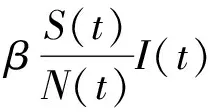
u1(t),u2(t)是两个控制函数，满足0≤ui≤1，i=1,2,用来刻画在治疗结核病人的过程中所采取的控制措施对于结核病人治愈率的影响.根据医学上鉴定结核病人的治愈标准：是指体内感染的结核杆菌的数量，所以假设结核病人治愈后重新成为潜伏感染者，一旦受到外界刺激、或者个体免疫力下降，仍有发病的可能性.根据结核病传播机理建立以下具有控制措施的结核病治疗模型：

(γ1+u1(t))(1-p)I(t)+(γ2+u2(t))pI(t)

(γ2+u2(t))pI(t)

(1)

2 基本再生数的敏感性分析

利用再生矩阵的方法[12]可以得到模型(1)的基本再生数：

R0(u1，u2)=

(2)

当u1(t)=u2(t)=0，模型(1)的基本再生数变为：

(3)

显然，R0>R0(u1,u2).这说明控制措施u1，u2是有效的，可以减小基本再生数R0.也就是，控制措施能够降低结核病的传播.选用表1中的参数值，利用偏秩相关系数方法(Partial Rank Correlation Coefficient,PRCC)对u1(t)=u2(t)=0时的基本再生数R0进行敏感性分析,如图1所示.图1显示，传染率、发病率以及染病者中耐药染病者所占的比例都与基本再生数R0成正相关；而死亡率、转阴率γ1和γ2都与R0成负相关.尽管传染率和发病率的正相关性最大，但是鉴于潜伏感染者不具有传染性，所以控制具有传染性的染病者的人数会有助于降低传染率，提高染病者的转阴率.

表1 各参数值的意义及取值范围

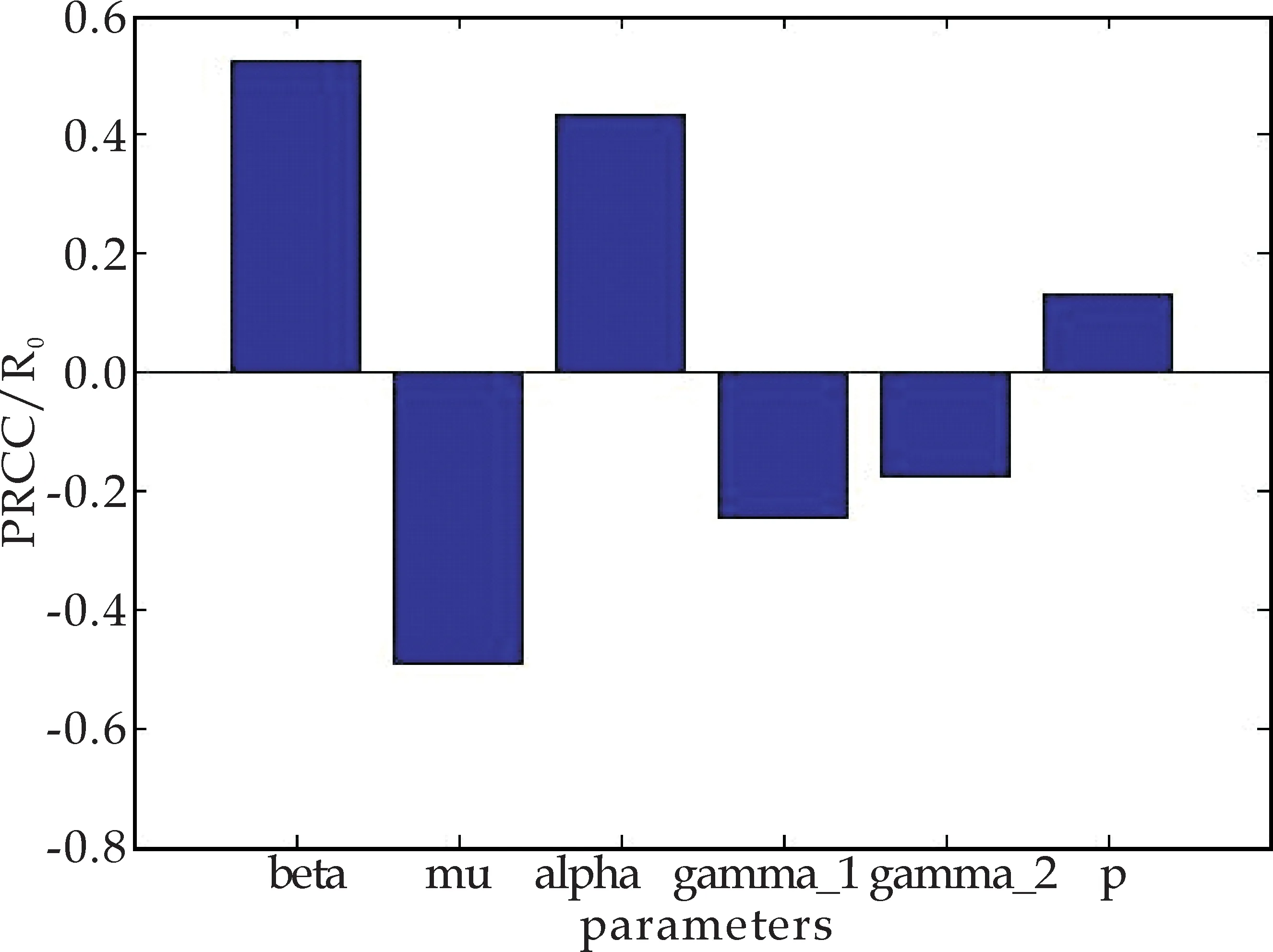
图1 基本再生数R0对应于各个参数的敏感性分析图

注释1对于任意参数，不等式R0(u1,u2)≤R0(0,u2)都成立.这是因为对R0(u1,u2)关于u1求偏导数可得：

因此，基本再生数R0(u1,u2)随着u1的增加而减小.

类似的，也可以得到，

也就是，R0(u1,u2)随着u2的增加而减小.

注释2基本再生数R0(u1,u2)会随着感染率β的增加而增加.这是因为对R0(u1,u2)关于β求偏导数可得：

所以，基本再生数R0(u1,u2)随着β的增加而增加.

3 控制措施

在本节中将利用庞特里亚金极大值原理来分析在结核病治疗过程中采取说服教育、跟踪、监督喝药、以及更换药物等措施对于减少结核杆菌感染者人数的有效性.

这里，u1(t)表示对非耐药染病者治疗时，医院或者病人家属雇佣一定的医护人员对非耐药病人采取说服教育、跟踪和监督用药等方式来管理病人，帮助病人完成医生制定好的治疗过程，提高转阴率.这些措施治愈结核病人的同时也可以避免染病者对治疗药物产生耐药性.结核病人中途停止治疗、或者不按医嘱治疗就会导致耐药发生，产生耐药染病者.u2(t)表示对耐药染病者治疗时，国家或耐药染病者自身有一定的经济能力可以调换更先进的治疗药物来抵制耐药，提高耐药染病者的治愈率.给出控制域为：

U={(u1,u2)∈L1(t0,tf)0≤ui≤1,i=1,2}

定义目标函数：

J(u1(t),u2(t))=

(4)

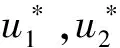
为了寻找最优解，定义Hamilton方程为：

(5)

其中λi(i=1,2,3)为伴随变量，满足方程：

(6)

横截条件为λi(tf)=0(i=1,2,3).利用最优控制条件，可得

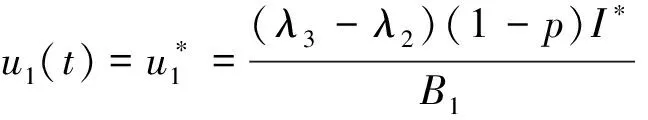
(7)

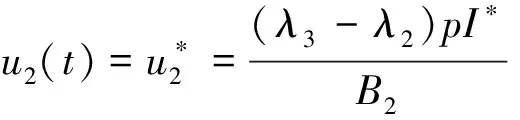
(8)

由于0≤ui≤1,i=1,2，利用控制域U，有以下三种情况出现：

因此有：

(9)

类似的，有：

(10)

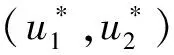
4 数值分析和讨论

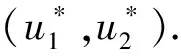
图2显示，当施行控制措施后，结核杆菌感染者(染病者与潜伏感染者)总数占人群的比例会减少.另外，为了减少结核杆菌感染者的总数，优化控制u1和u2的会在大约1.5年左右的地方到达最大值，随后的时间里都会呈现随时间下降到最小值,如图3所示.

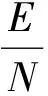
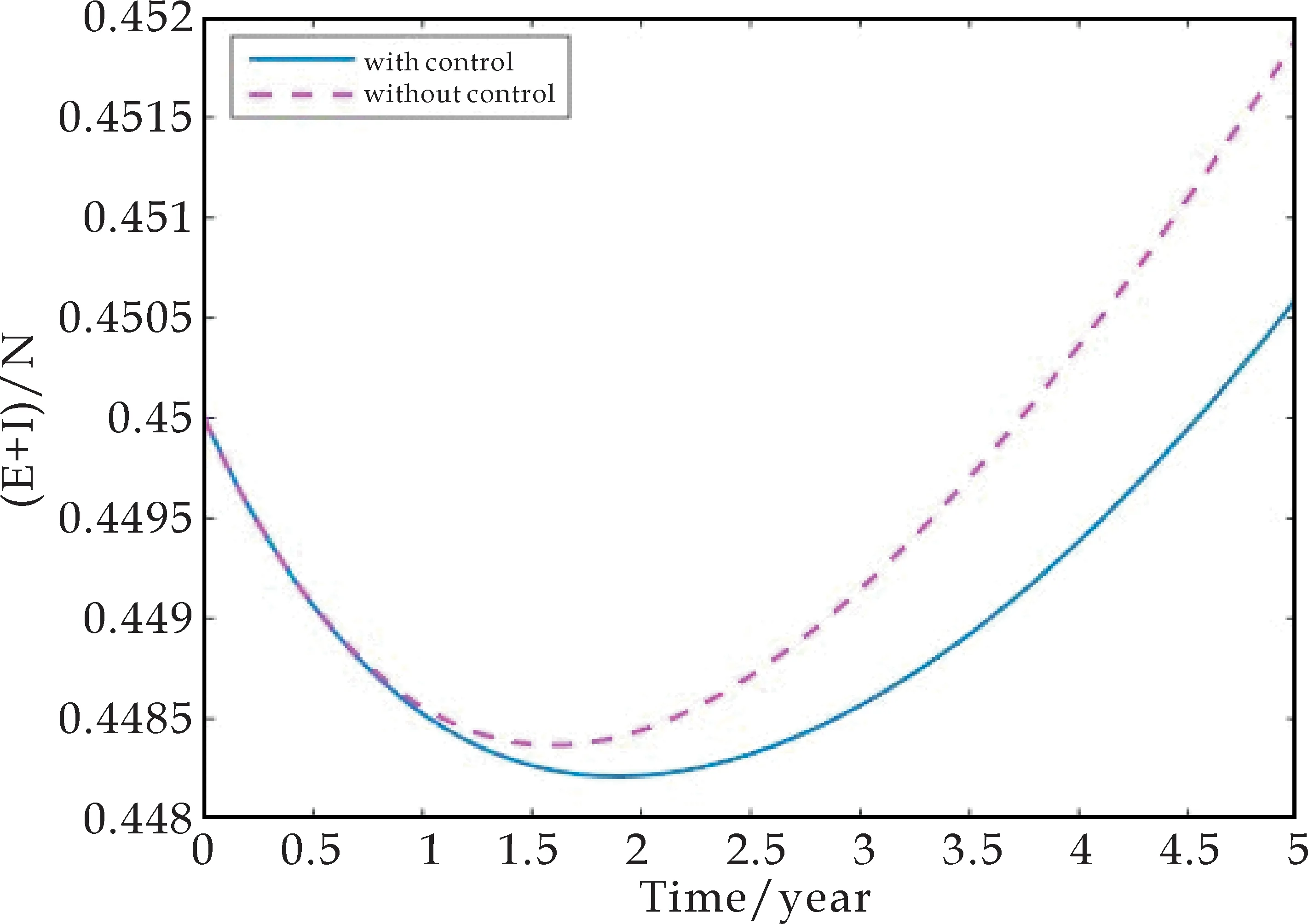
图2 有控制和无控制的情况下感染者所占的比例

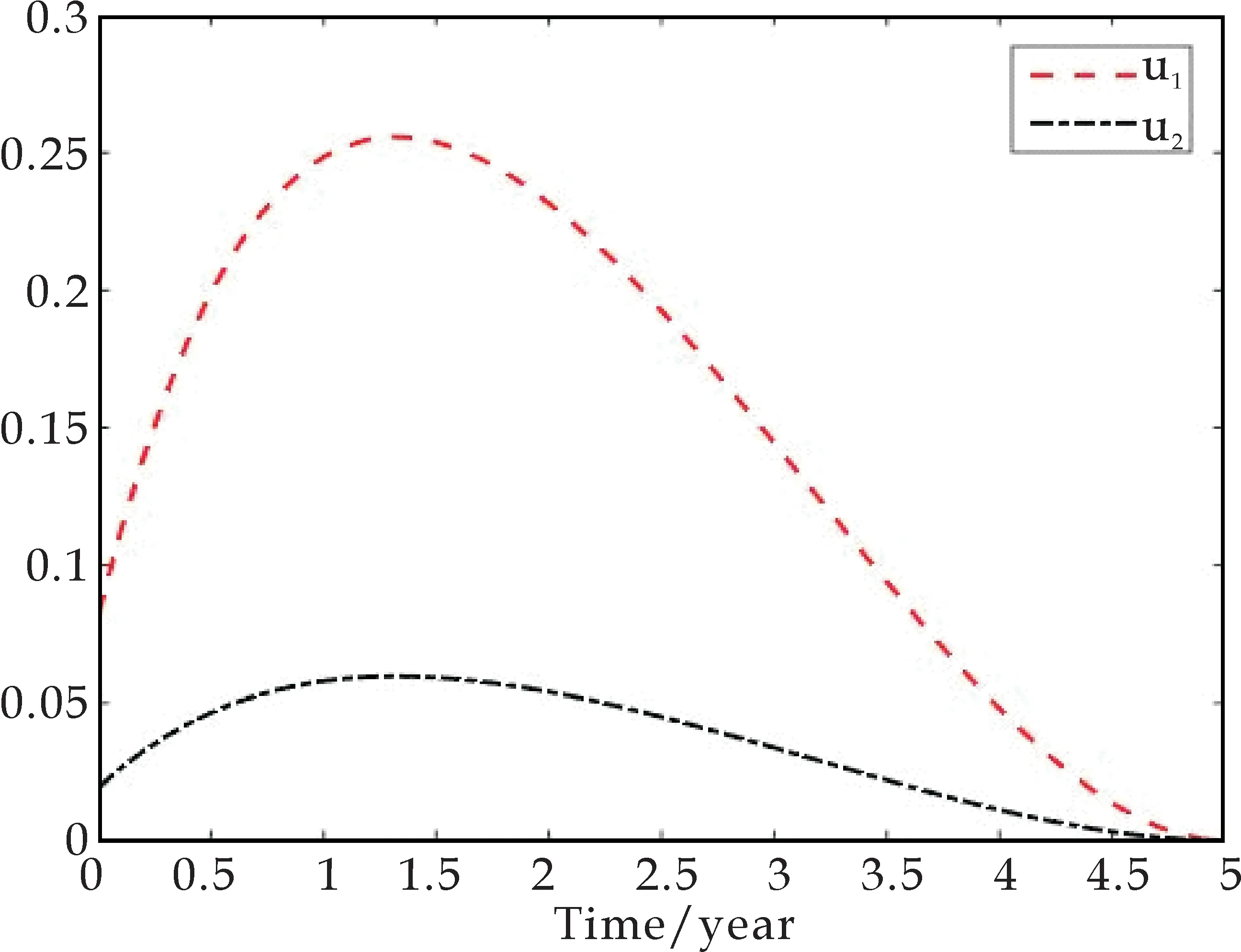
图3 控制u1(t),u2(t)随时间变化的曲线

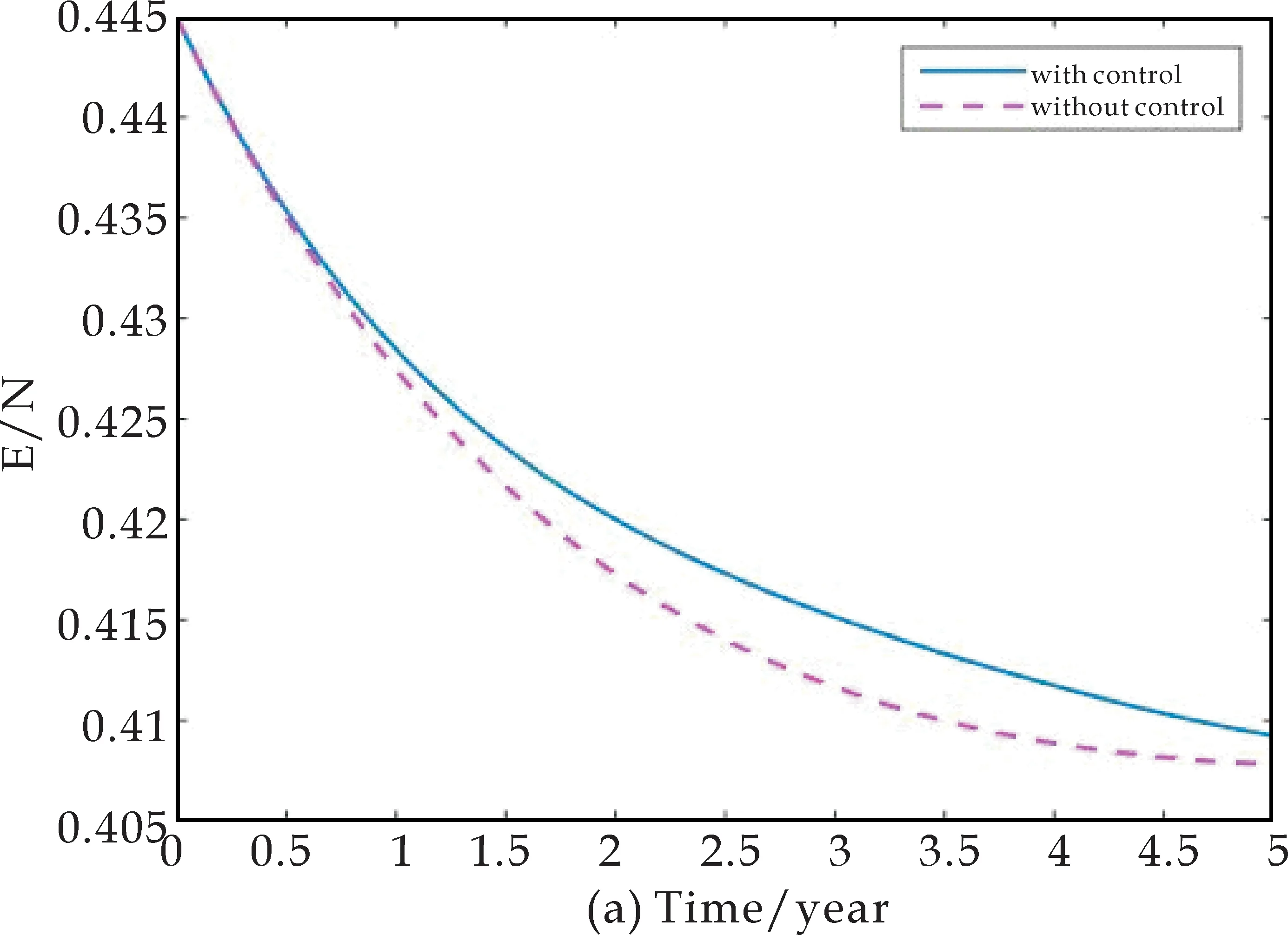
图4 有控制和无控制的情况下潜伏感染者、染病者所占比例的变化

继续考虑随着染病者的治愈率的不断变化，控制措施的变化情况，以及相应的感染者人数的变化情况.先确定γ2=0.2，分别令γ1=0.9，γ1=0.7和γ1=0.5，得到图5.图5显示随着非耐药染病者治愈率的下降，控制措施u1(t)和u2(t)都需要加强，才能有助于结核杆菌感染者在人群中所占的比例下降，也就是感染人数的下降.

另外，图5(a)显示，如果非耐药治愈率越高，对于非耐药病人可实施的控制措施的空间越小；图5(b)的数值结果显示，随着非耐药治愈率γ1的提高，大量的染病者会被医学治愈成为潜伏感染者.相应的，有传染性的结核病人数会降低，结核病的传染源得到有效控制，无需继续加强对耐药病人的控制措施也可有效控制感染者(潜伏感染者与染病者之和)在整个人群中所占的比例.

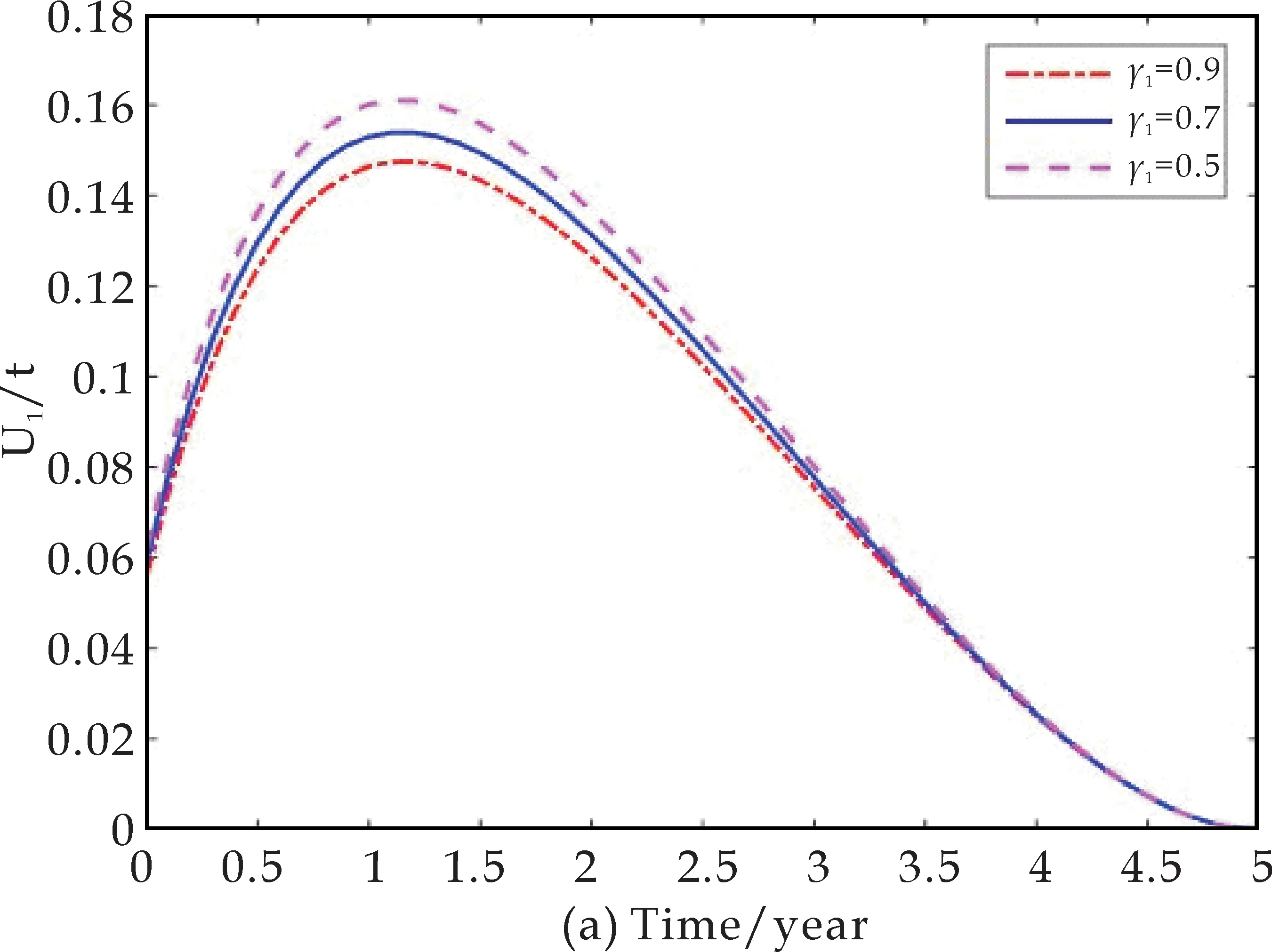
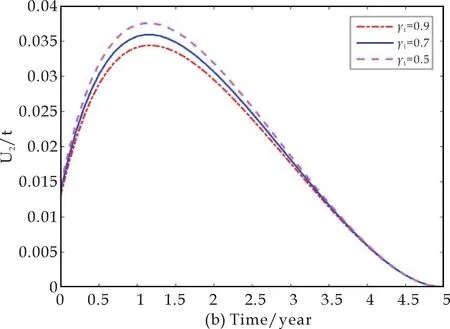
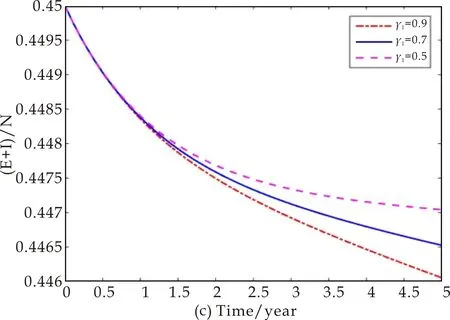
图5 随着γ1的变化，控制措施以及感染者人所占比例的变化

类似地，取定γ1=0.9，再分别令γ2=0.1，γ2=0.2和γ1=0.3，来考虑随着耐药染病者的治愈率变化，控制措施的变化情况，以及相应的感染者人数的变化情况,如图6所示.图6显示，随着耐药染病者治愈率的下降，为了减少结核感染者的人数，需要加强控制措施u1(t)和u2(t).

图5(c)中的点划线与图6(c)中的实线是在同一组参数下得到的.图5(c)和图6(c)通过数值模拟的方式给出了γ1和γ2在取不同数值的情况下，所实施的不同控制措施对于控制感染者(潜伏感染者与染病者之和)所占比例的效果.

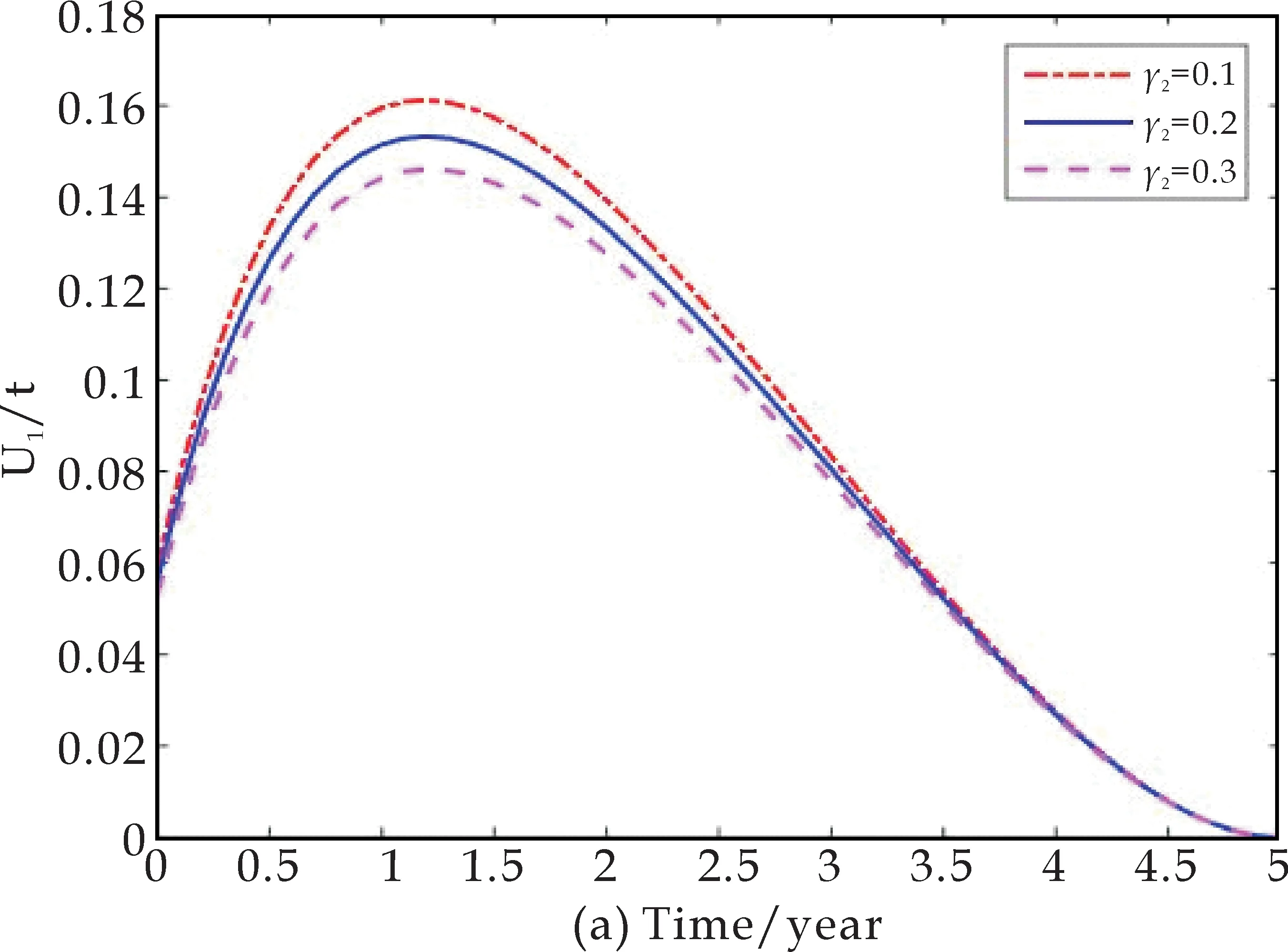
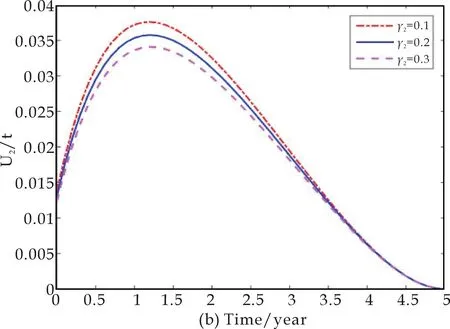
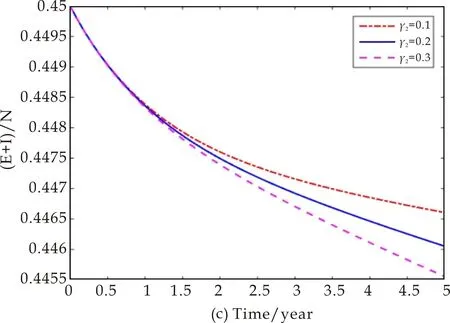
图6 随着γ2的变化，控制措施以及感染者人所占比例的变化

5 结论

本文讨论了模型的非耐药和耐药的优化治疗控制措施，得到了使得目标函数取得最小值的最优控制对，当施行控制措施后，结核杆菌感染者(染病者与潜伏感染者)总数占人群的比例会减少；随着非耐药染病者治愈率的下降，控制措施u1(t)和u2(t)都需要加强，才能有助于结核杆菌感染者在人群中所占的比例下降，也就是感染人数的下降；随着耐药染病者治愈率的下降，为了减少结核感染者的人数，需要加强控制措施u1(t)和u2(t)；随着非耐药治愈率γ1的提高，大量的染病者会被医学治愈成为潜伏感染者.相应的，有传染性的结核病人数会降低，结核病的传染源得到有效控制，无需继续加强对耐药病人的控制措施也可有效控制感染者(潜伏感染者与染病者之和)在整个人群中所占的比例.

[1] Gunnar Bjune.Tuberculosis in the 21 st century:An emerging pandemic[C]//Global health research/Global helse.Norsk:Norsk Epidemiologi,2005:133-139.

[2] World Health Organization.Global Tuberculosis Report 2017

[DB/OL].http://www.who.int/tb/publications/global_report/en/,2017-10-30.

[3] 全国结核病流行病学抽样调查技术指导组.2010年全国第五次结核病流行病学抽样调查报告[J].中国防痨杂志,2012,34(8)：485-508.

[4] Castillo Chavez C,Song B J.Dynamical models of tuberculosis and their applications[J].Math.Biosci.Eng.,2004,1(2):361-404.

[5] 马知恩,周义仓,王稳地,等.传染病动力学的数学建模与研究[M].北京：科学出版社，2004.

[6] Lloyd Smith J O,George D,Pepin K M,et al.Epidemic dynamics at the human-animal interface[J].Science,2009,326:1 362-1 368.

[7] Jung E,Lenhart S,Feng Z.Optimal control of treatments in a two-strain tuberculosis model[J].Discrete Contin.Dyn.Syst.Ser.B,2002,2(4):473-482.

[8] Hattaf K,Rachik M,Saadi S,et al.Optimal control of tuberculosis with exogenous reinfection[J].Appl.Math.Sci.(Ruse),2009,3(5-8):231-240.

[9] Bowong S.Optimal control of the transmission dynamics of tuberculosis[J].Nonlinear Dyn.,2010,61(4):729-748.

[10] F Boulahbal,P Chaulet.Tuberculosis in Africa:Epidemiology and control measures[J].Medecine Tropicale,2004,64(3):224-228.

[11] Cristiana J Silva,Delfim F M Torres.Optimal control for a tuberculosis model with reinfection and post-exposure interventions[J].Math.Biosci.,2013,244:154-164.

[12] P Van Den Driessche,J Watmough.Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J].Math.Biosci.,2002,180:29-48.

[13] Hui Cao,Yicang Zhou.The discrete age-structured SEIT model with application to tuberculosis transmission in China[J].Mathematical and Computer Modelling,2012,55:385-395.