基于改进粒子滤波算法的水下目标跟踪

周伟江，董 博，许伟杰

(1. 中国人民解放军92493部队，辽宁葫芦岛125000；2. 中国科学院声学研究所东海研究站，上海200032)

0 引 言

目标运动分析(Target Motion Analysis，TMA)对于水下作业的开展具有重要意义。在被动测量的情况下，仅利用目标的方位信息来实时估计运动目标参数的过程被称作纯方位目标运动分析(Bearings-only Target Motion Analysis，BO-TMA)[1]。水下被动目标跟踪问题具有非线性和弱可观性的特点，这导致了算法处理困难。

粒子滤波是一种基于蒙特卡洛(Monte Carlo)和递推贝叶斯估计的方法，不受模型非线性和非高斯噪声的限制。理论上只要粒子足够多，就能较为精确的表达观测量及状态的后验分布。但根据大量的研究和实验表明，粒子数目能够显著影响粒子滤波算法的性能及其复杂度。采用较多的粒子数可以获得良好的滤波效果，但其复杂度可能对于系统资源提出挑战。在保证一定滤波精度的前提下，应尽量减少粒子数目[2-6]。

本文将KL距离(Kullback-Leibler Divergence)[7]引入粒子滤波重采样的过程中，改进了常规粒子滤波算法中粒子数目不能自适应改变的问题，在保证滤波性能的同时提高了计算效率，并在纯方位水下目标跟踪情况下，对所提算法进行了仿真实验，取得了较好的跟踪性能。

1 常规粒子滤波

1.1 非线性滤波模型

通常动态系统的状态空间模型可以用状态转移方程和状态观测方程进行描述：

式中：f(⋅)和h(⋅)分别表示状态转移函数和观测函数，xk表示k时刻的系统状态向量，zk表示k时刻的观测向量，wk和vk分别表示过程噪声和观测噪声。

1.2 粒子滤波算法

粒子滤波算法是通过非参数化的蒙特卡洛方法来实现递推的贝叶斯估计，其实质是由加权的随机样本即粒子组成离散的随机测度来近似相关概率分布[2-3]。

贝叶斯滤波包括预测和更新两个步骤。在预测阶段，需要估计状态的先验概率密度，在更新阶段，使用新的观测值来修正先验概率密度，进而获得后验概率密度。

(1) 预测过程，根据获得

如果状态xk只与有关，可得：

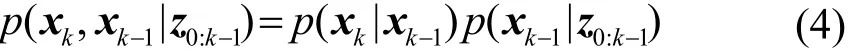
对进行积分，可得:

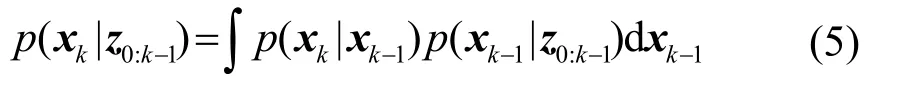
其中表示0至k-1时刻的观测向量.

(2) 更新过程，需要通过得到

在得到最新观测值zk后：

假设观测值只由状态值决定，那么：

因此，

式中表示归一化常数：

在贝叶斯滤波递推的过程中需要计算积分，粒子滤波就是其中一种估计方法。

在粒子滤波中，假设可以从后验概率密度中抽取N个相互独立、分布相同的随机样本则后验概率分布可以近似地表示为

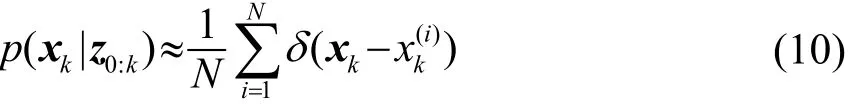
其中，z0:k表示0至k时刻的观测向量，当时，

然而，通常无法直接从后验概率分布中采样，因此引入一个便于采样的重要性概率密度函数从中抽取样本粒子

则后验概率密度可以表示为

经过数次迭代后，只有少数粒子的权值较大，状态空间中的有效粒子数较少，使得估计性能下降，需要进行重采样的操作，以便改善权值退化的现象。

由此，任意函数的期望值估计可以表示为

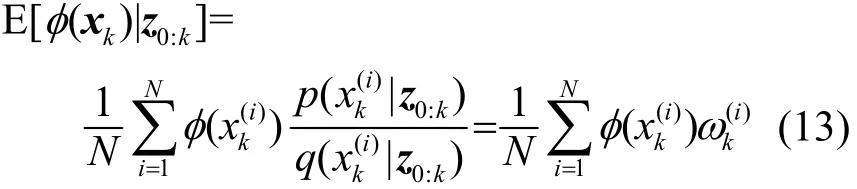
1.3 常规粒子滤波算法流程

根据1.2节中粒子滤波算法原理，可以得到常规粒子滤波算法的流程如下：

步骤1：初始化。对于i= 1 ,2,… ,N，由先验概率p(x0) 生成初始粒子集合

步骤2：重要性采样。对由重要性概率密度函数生成采样粒子

步骤4：重采样。计算有效粒子数判断是否需要进行重采样。如不需要，则进行步骤5；否则，对粒子集合进行重采样，重采样之后的粒子集合为

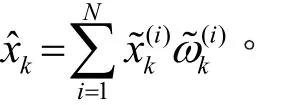
2 改进的粒子滤波算法

常规前述的粒子滤波算法在计算过程中，粒子数目是保持不变的，恒定的样本容量会直接影响到算法的实时性和计算精度。较大的粒子数目会带来精度的提升，但同时也会增加计算负担，不满足应用中的实时性需求；反之，较小的粒子数目虽然加快了计算速度，但又不能满足滤波精度的需求。因此，选择合适的滤波性能测度，使得粒子滤波算法在估计过程中能根据测度自适应地改变粒子数目是非常重要的。

华盛顿大学的Fox在文献[8]中，提出了一种基于KLD采样的自适应粒子滤波算法，利用KL距离来描述粒子滤波的近似误差，根据样本的近似分布与真实分布之间的KL距离来调整粒子数目。该方法隐含地假设样本从真实分布中抽取，并没有考虑真实后验分布与重要性概率密度分布之间的差异。

本文提供了一种改进的算法，在粒子滤波重采样的过程中引入了 KLD方法。该算法确定了需要进行重采样的粒子数目，以保证在重采样前和重采样后粒子分布的KL距离不超过某一差异阈值。从而，当概率密度集中在状态空间中的某区域时，需要重采样较少的粒子数，而当概率密度分散在状态空间的绝大部分区域时，需要重采样较多的粒子数。

下面先从信息论的角度对于粒子数目自适应机制的有效性加以说明，然后给出粒子数目自适应的算法。

2.1 Kullback-Leibler距离

KL(Kullback-Leibler)距离是评价数据之间偏差程度的测度，它的定义见式(14)[7]：

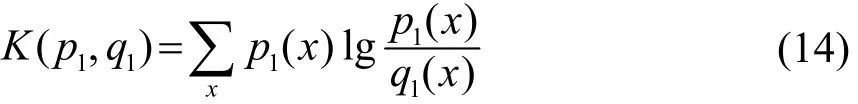
K可以用来表示不同的概率分布p1与q1之间的接近程度，该值越小，表示p1越接近于q1。

根据文献[8-10]中的推导，使用p1(x)表示基于样本的最大似然后验概率分布，q1(x)表示真实的后验概率分布，为了保证它们之间的KL距离不超过一定的差异阈值ε，样本数目n应该满足如式(15)所示的关系：

根据卡方分布[11]的分位数关系，得到式(16)：

式中表示具有个自由度的χ2分布表示自由度为k-1的1-δ分位数。

于是选择样本数目n如式(17)，就可以1-δ的概率保证基于样本的最大似然后验概率分布与真实的后验概率分布之间的KLD不超过ε，即

通常，由Wilson-Hilferty变换，可以得到n的近似计算表达式：

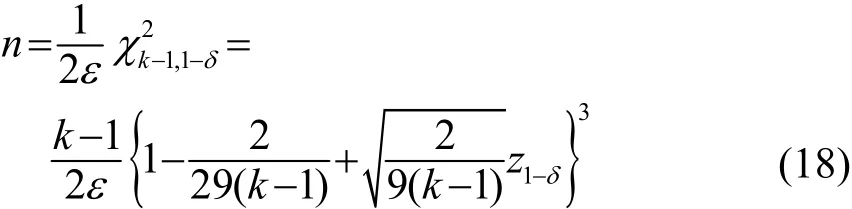
式中，z1-δ为标准正态分布的1-δ上侧分位数。

2.2 基于KLD重采样的改进粒子滤波

本文的改进算法在重采样的过程中，使用式(18)确定需要进行重采样的粒子数目。将粒子集分割成多个小区域{bk'}，然后根据粒子的权重进行分段重采样，直到粒子数目满足式(18)的要求。这就保证了粒子数目能够与概率密度在状态空间的集中程度相一致。同时，由于改进算法是在重采样的过程中参照粒子权重采用 KLD方法，正好符合从后验概率分布中抽取，从而避免了上文提到的之前KLD采样当中的问题。

针对上述改进的粒子滤波算法，其算法流程如下：

步骤1：初始化。对于由先验概率p(x0)生成初始粒子集合输入预测后验概率密度与真实后验概率密度间的KL距离差异阈值ε，标准正态分布的上分位数z1-δ，小区域尺寸阈值L，最大粒子数目Nmax，k时刻的预测粒子集合Pk=Φ，k'=0，n=0。

步骤3：权值更新。计算粒子权值并进行归一化。

步骤4：重采样。根据权值对于表示的粒子集合进行抽取，将新的粒子添加到集合中，更新抽取粒子数n，令

判断新抽取的粒子是否属于空的小区域bk'，如果属于，则更新区域序号k'，令k'=k'+1；将bk'标识为已进行重采样区域；根据式(18)计算样本数目N'：

如果，则跳转到步骤4。否则转到步骤5。

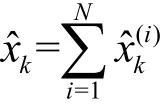
3 仿真实验及分析

3.1 水下目标机动模型

纯方位目标跟踪中只利用含有噪声的目标方位信息来估计目标的位置和速度参量。跟踪系统的离散状态方程和观测方程可以分别表示为

其中为目标状态向量；zk为方位的观测向量；wk和υk分别为过程噪声和观测噪声；F为状态转移矩阵；G为过程噪声转移矩阵，其中T为采样周期。

F的选择与目标的机动模型相关，常见的机动模型包括：恒速度模型(Constant Velocity，CV)、恒加速度模型(Constant Acceleration, CA)、恒转向模型(Constant Turn，CT)、Singer模型、当前机动模型等。本文涉及到的是CV模型和CT模型[12]。

在CV模型下，状态转移矩阵F可以表示为式(21)：

在CT模型下，状态转移矩阵F可以表示为式(22)：

其中：ω为角速度，T为采样周期。

3.2 仿真与分析

为了验证改进的粒子滤波算法在纯方位水下目标跟踪中的性能，我们分别使用常规粒子滤波算法和改进粒子滤波算法对于目标在不同机动状态下的跟踪效果进行了比较研究。

仿真时长为100 s，采样周期1 s，粒子数目N为1000。目标初始位于(1000，1000) m处，开始按照CV模型以初始速度(15,-10) m.s-1做匀速直线运动，60 s后按照CT模型改做2.5°/s的匀速转弯运动。系统噪声和观测噪声均为独立的零均值高斯白噪声，系统噪声的距离均方差σr为10-1m，速度均方差σv为10-2m.s-1，方位角的观测均方差为0.5°。

在上述条件下进行500次蒙特卡洛仿真，获得改进粒子滤波算法与常规粒子滤波算法对目标的轨迹跟踪曲线如图1所示；按照公式(23)定义的目标位置均方根误差(Root Mean Square Error，RMSE)，两种算法的RMSE对比曲线如图2所示；计算所需的粒子数目的对比曲线如图3所示。

由图1可知，采用改进的自适应粒子滤波算法，跟踪曲线与真实轨迹吻合度较高，能有效地完成跟踪任务；由图2和3可知，在第一部分匀速直线运动中(60s以前)，常规粒子滤波算法和改进粒子滤波算法均能获得较好的误差性能，但是改进型粒子滤波所需要的粒子数目更少，能够节省更多的计算资源；当进入第二部分(60s以后)匀速转弯阶段，两种算法的误差均有所增大，但是改进型粒子滤波算法自适应地增大了粒子数目，更好地控制了误差(见图2)，在机动状态改变的过程中体现了较好的效果。由此可见，改进的粒子滤波算法能够有效地适应水下跟踪的多变环境，具有良好的跟踪性能。

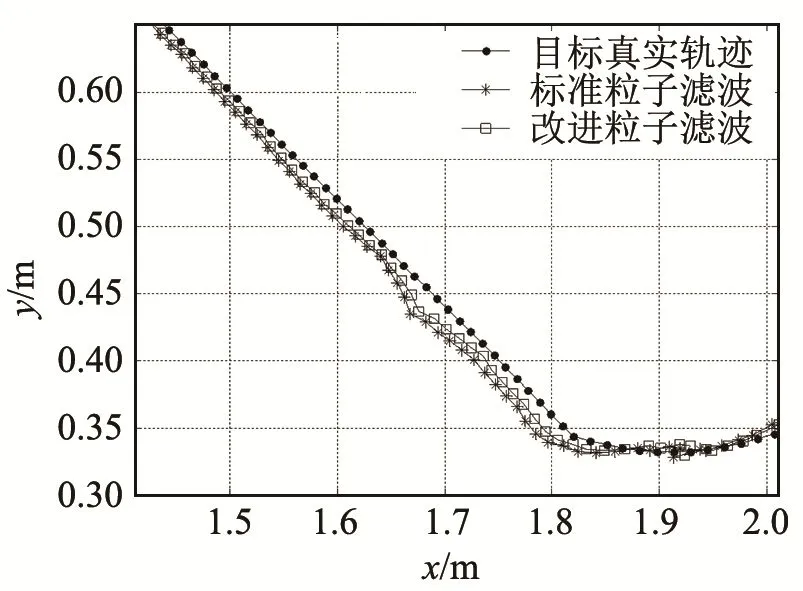
图1 两种粒子滤波算法跟踪曲线Fig.1 Target tracking scenes of two different methods

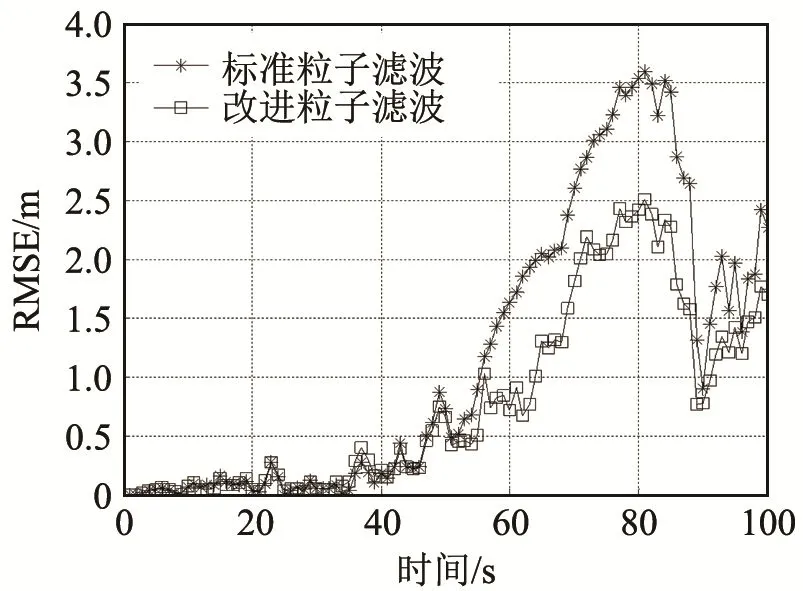
图2 两种粒子滤波算法的RMSE比较Fig.2 RMSE Comparison of two different methods

图3 两种粒子滤波算法所需的粒子数目比较Fig.3 Comparison of particle numbers in two different methods

在改进的粒子滤波算法中，计算所需的平均粒子数目与KL距离的差异阈值ε以及小区域尺寸阈值L有很大的关系。设置不同的参数取值，进行500次蒙特卡洛仿真，得到结果如图4和图5所示。由图4可知，随着所设置的差异阈值不断变大，改进的粒子滤波算法所需要的粒子数目逐渐变小(见图4(a))，同时均方根误差逐渐增大(见图4(b))。图5表明，随着设置的小区域尺度阈值不断变大，粒子数目逐渐变小(见图5(a))，均方根误差变大(见图5(b))，但是改变小区域尺度阈值对于粒子数目的影响不如改变KL距离的差异阈值对粒子数目的影响大。因此，可以根据系统对于精度的需求，选择合适的差异阈值和尺度阈值，从而兼顾效率与精度。

图4 KL距离差异阈值与粒子数和RMSE的关系Fig.4 Curves of particle numbers and RMSE in different KLD error bound threshold

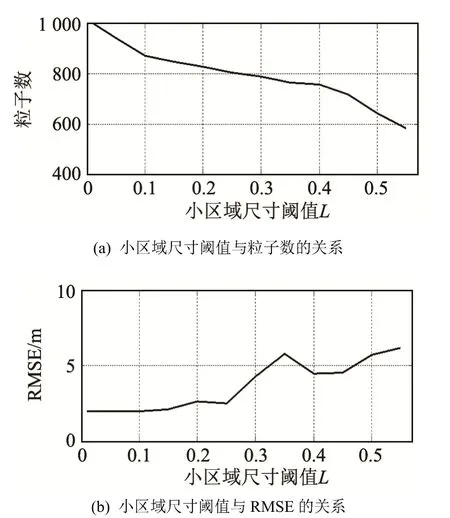
图5 小区域尺寸阈值与粒子数和RMSE的关系Fig.5 Curves of particle numbers and RMSE in different bin size

4 结 论

本文针对常规粒子滤波过程中粒子数目不能自适应改变的问题，提出了一种基于KL距离重采样的改进粒子滤波算法，它能够保证在一定滤波精度前提下，自适应地调整粒子数目大小，提高了粒子滤波方法对环境的适应能力，并将该算法应用于水下目标的跟踪问题中。通过仿真实验，证明该方法在达到较好跟踪效果的同时，避免了常规粒子滤波算法计算量膨胀的问题，工程实现简单，适合实际应用。

参考文献

[1] MUSICKI D. Bearings only muti-sensor maneuvering target tracking[J]. Syetems and Control Letters, 2008, 57(3): 216-221

[2] 朱志宇. 粒子滤波算法及其应用[M].北京: 科学出版社, 2010,1-10, 114-125.ZHU Zhiyu. Particle Filter Algorithm and Application[M]. Beijing: Science Press, 2010, 1-10, 114-125.

[3] ARULAMPALAM M S, MASKELL S, GORDON N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Transactions on Signal Processing,2002, 50(2): 174-188.

[4] 常发亮, 马丽, 刘增晓, 等. 复杂环境下基于自适应粒子滤波器的目标跟踪[J]. 电子学报, 2006, 12(12): 2150-2153.CHANG Faliang, MA Li, LIU Zengxiao, et al. Target Tracking Based on Adaptive Particle Filter Under Complex Background[J].Acta Electronica Sinica, 2006, 12(12): 2150-2153.

[5] CLOSAS P, C. Fernandez-Prades. Particle filtering with adaptive number of particles[C]//IEEE Aerospace Conference, 2011, 1-7.

[6] CORNEBISE J, MOULINES É, OLSSON J. Adaptive methods for sequential importance sampling with application to state space models[J]. Statistics and Computing, 2008, 18(4): 461-480.

[7] 麦克尔里思. 信息论与编码理论[M]. 北京: 电子工业出版社.2006.

[8] FOX D. Adapting the sample size in particle filters through KLD-Sampling[J]. International Journal of Robotics Research,2003, 22(12): 985-1003.

[9] SOTO A. Self adaptive Particle Filter[C]//Proceedings of International Joint Conferences on Artificial Intelligence, 2005, 1398-1406.

[10] LI T, SUN S, SATTAR T. Adapting sample size in particle filters through KLD-resampling, electronics letters[J]. Electronics Letters,2013, 49(12): 740-742.

[11] 武爱文, 冯卫国, 卫淑芝, 等. 概率论与数理统计[M]. 上海: 上海交通大学出版社, 2011.

[12] 孙仲康, 郭福成, 冯道旺, 等. 单站无源定位跟踪技术[M]. 北京:国防工业出版社, 2008, 205-220.SUN Zhongkang, GUO Fucheng, FENG Daowang, et al. Passive location and tracking technology by single observer[M]. Beijing:National Defend Industy Press, 2008, 205-220.