On Quasi-Chebyshevity Subsets of Unital Banach Algebras

M.Iranmanesh and F.Soleimany

Department of Mathematical Sciences,Shahrood University of Technology,P.O.Box 3619995161-316,Shahrood,Iran

1 Introduction

The subject of approximation theory is an old branch of analysis and has attracted the attention of several mathematicians during last years.This theory which has many important applications in mathematics and some other sciences has been studied by many authors,e.g.,[4,15].A basic problem in the theory is”Given a pointxand a setWin normed spaceX,determine a pointw0ofWwhich is at a minimum distance fromx”i.e.to findw0∈Wsuch that

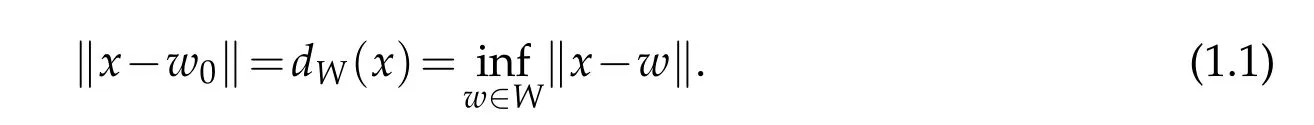
The set of all best approximations toxfromWis denoted by PW(x).Thus

If eachx∈Xhas at least one best approximation inW,thenWis called a proximinal set andWis said to be non-proximinal if PW(x)=∅for somex∈XW.A problem which has been intensively studied is to check whether a Banach spaceXdoes or does not contain bounded closed non-proximinal sets.The results in general Banach spaces can be found in[1,5,6].A subsetWof a Banach spaceXis called quasi-Chebyshev if PW(x)is a non-empty and compact set inXfor everyx∈X(see[10]).Some results on characterizations of quasi-Chebyshev subspaces in Banach spaces can be found in[9,10].In the paper,we introduce the problem exist non-quasi-Chebyshev and non-pseudo-Chebyshev sets in unital Banach algebras.All this works done by applying the related fixed point and approximation theory results.We give characterizations of quasi-Chebyshev subalgebras inC∗-algebras in terms of substate function.The structure of this paper is as follows.In Section 2 we records some facts about Banach algebras,spectral properties ofC∗-algebras A and HilbertC∗-modules.In Section 3,we approach the question on the existence of non-quasi-Chebyshev sets in unital abelian Banach algebras by using the related fixed points and invariant approximation results.As a consequence,we obtain some results on the algebra of continuous functionsC(S),whereSis a compact set.We show that every closed bounded convex set in aC∗-algebra A is quasi-Chebyshev if and only if A be finite dimensional.Similarly,we get some results for HilbertC∗-modules.Best approximation and quasi-Chebyshev of subalgebra inC∗-algebras,is discussed and characterized in Section 4.

2 Preliminaries

Let us start with some basic definitions,which will be used later.Consider A as a unital algebra with the unite.If A is a Banach space with respect to a norm which satisfies the multiplicative inequality

then the pair(A,k·k)is called a normed algebra.A complete unital normed algebra is called unital Banach algebra.a∈A is said to be invertible if there is an elementbin A such thatab=ba=e.The fields of real and complex numbers are denoted by R and C,respectively.The symbolFdenotes a field that can be either R or C.The spectrum of an elementxof a unital algebra A overFis the set

The spectral radius ofxis defined by

A nonzero homomorphismτ:A→F,where A is a unital algebra overF,is called a character.We denote by Ω(A)the set of all characters on A.If A is a unital abelian Banach algebra andx∈A,we define a continuous function bxby

We callthe Gelfand transform ofx.We denote bythe set{:x∈A}.It is easy to see

thatis self-adjoint if and only if for eachx∈A,there exists an elementy∈A such thatτ(x)=for eachτ∈Ω(A).If A is a unital abelian complex Banach algebra,Ω(A)6=∅andσ(a)={τ(a):τ∈Ω(A)}for alla∈A.If A is a unital Banach algebra,then Ω(A)is compact(see[11]).We follwed with the concept ofC∗-algebras.An involution ∗on an algebra A is a mappingx→x∗from A onto A such that(λx+y)∗=+y∗,(xy)∗=y∗x∗and(x∗)∗=x,for allx,y∈A andλ∈C.An involutive Banach algebra is called a Banach∗-algebra.A Banach ∗-algebra A is said to be aC∗-algebra if kxx∗k=kxk2,for eachx∈A.Clearly under the norm topology onB(H),the set of all bounded linear operators on a Hilbert spaceHis aC∗-algebra relative to involutionT→T∗,which is defined by

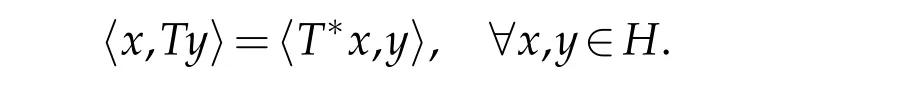
Let A be an algebra then Mn(A)denotes the algebra of alln×n-matricesa=[aij]with entriesaijin A.If A is aC∗-algebra,so Mn(A),where the involution is given byIf A and B be twoC∗-algebras,we denote by A⊗B their algebraic tensor product.Note that for anyC∗-algebra one can identify the space Mn(A)with the tensor product Mn(C)⊗A.

A(right)HilbertC∗-moduleVover aC∗-algebra A is a linear space which is a right A-module equipped with an A-valued inner-producth·,·i:V×V→A that is sesquilinear,positive definite and respects the module action,i.e.,

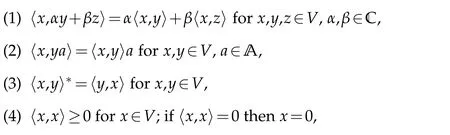
andVis complete with respect to the norm defined by kxk=khx,xik12,for eachx∈V.

Lemma 2.1(see[3]).Let E be a C∗-module over a C∗-algebraA.Then E can be isometrically embedded in B(H,K),where H,K are Hilbert spaces.

In the following,we recall some useful lemmas in fixed point theory that will be needed in the sequel.Let(X,·k)be a Banach space,A mappingT:E⊆X→Xis nonexpansive if kTx−Tyk≤kx−yk for eachx,y∈E.The fixed point set of mappingTis denoted by F(T)={x∈X:T(x)=x}.

Lemma 2.2(see[14]).Let X be a Banach space,C a compact convex subset of X and T:C→C a continuous map.Then T has at least one fixed point in C.

Definition 2.1(see[8]).LetKbe a convex subset of a Banach spaceX.A mapV:K→Xis called convex if

Lemma 2.3(see[8]).Let K be a non-empty weakly compact convex subset of a Banach space X and let T:K→X be non-expansive and suppose I−T is convex on K.Then T has a fixed point.

3 A non-quasi-Chebyshev sets of Banach algebras

In this section,we consider closed,convex and bounded subsets of infinite dimensional unital Banach algebras and show with regard to the general conditions that these sets are not quasi-Chebyshev and pseudo-Chebyshev.

Definition 3.1.A closed subsetWof a normed linear spaceXis called non-quasi-Chebyshev if it is not quasi-Chebyshev.

Definition 3.2.LetUbe a closed subset of a normed linear spaceX.ThenUis calledω-quasi-Chebyshev if the set PU(x)is non-empty and weakly compact for allx∈XU.AndUisω-non-quasi-Chebyshev if it is notω-quasi-Chebyshev.

Definition 3.3.LetXbe a Banach algebra,we sayXhas property(N)if Ω(X)6=∅ and forx,y∈X,|τ(x)|≤|τ(y)|for eachτ∈Ω(X)implies that kxk≤kyk.

Fupinwong and Dhompongsa studied the fixed-point property of unital commutative Banach algebras over a fieldF(see[7]).They obtained the following results.

ConsiderXas an infinite-dimensional unital abelian Banach algebra,which has property(N)such thatbXis self-adjoint and

then

(1)there exists a sequence{xn}∈Xsuch that

For eachn∈N,andis a sequence of non-empty pairwise disjoint subsets of Ω(X).

(2)Consider the mappingTnonXby

and sets

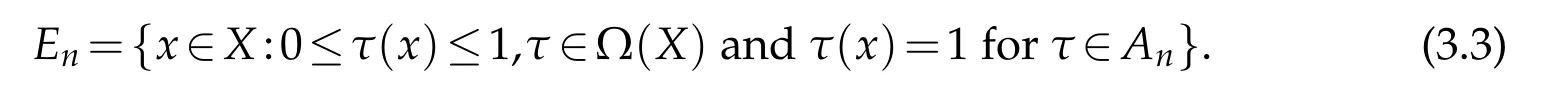
ThenTnhasn’t any fixed-point inEn.

Theorem 3.1.Let X be an infinite dimensional unital abelian Banach algebra with property(N)such thatis self-adjoint and satisfying(3.1),then X contains a non-quasi-Chebyshev subset(Moreover,X contains a non-w-quasi-Chebyshev set).

Proof.Assume on the contraryXand every of its closed subsets be quasi-Chebyshev(ωquasi-Chebyshev).LetTnandEndefined by(3.2)and(3.3).SinceXhas property(N)and|τ(xn)|≤1=τ(e)then kxnk≤1 forn∈N.Forx,y∈X,we have

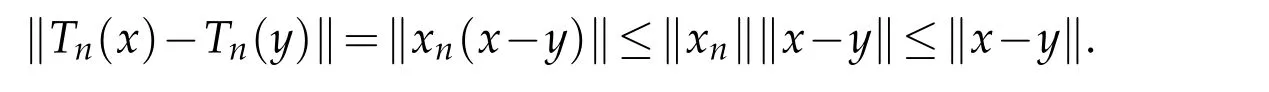
ThenTnis non-expansive onX.Forn∈N,Enis aTn-invariant convex set ofX,then forx∈X,PEn(x)is convex and by assumption is non-empty compact(weakly compact)set.We show that forx=0,PEn(0)isTn-invariant so.Lety∈PEn(0),furthery∈Enand thenTnyis inEnsinceTn(En)⊆En.AsTnis non-expansive,it follows that forg∈En,

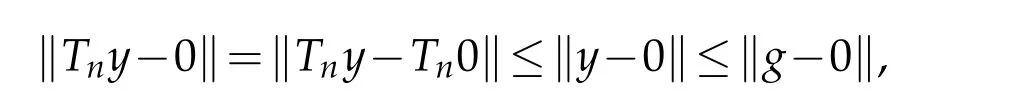
and thereforeTnyis in PEn(0).ThusTnmaps PEn(0)into itself.On the other hand,since the multiplication operation(a,b)→abis jointly continuous in Banach algebras.ThenTnis a continuous map.AsI−Tnis convex by applying Lemma 2.2 and Lemma 2.3 there existpn∈PEn(0)∩F(Tn)for eachn∈N.Thereforepn∈En∩F(Tn).But this is a contradiction by part(2)of the results of Fupinwong and Dhompongsa.

Definition3.4.A closed subsetWof a normed linear spaceXis called pseudo-Chebyshev,if the set PW(x)be a non-empty and finite-dimensional subset ofXfor allx∈XW.

A closed subsetWof a normed linear spaceXis non-pseudo-Chebyshev if it is not pseudo-Chebyshev.

Theorem 3.2.Let X be an infinite dimensional unital abelian Banach algebra with property(N)such thatis self-adjoint and satisfying(3.1).Then X has an non-pseudo-Chebyshev subset.

Proof.Assume on the contrary thatXand every of its closed subsets are pseudo-Chebyshev.LetTnandEnbe in such as(3.2)and(3.3).First we show thatEnis a bounded set for eachn∈N.Forx∈En,

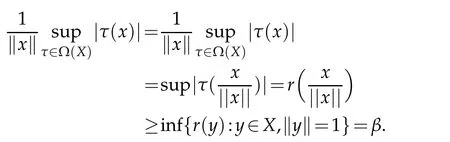
Since Ω(X)is compact there is a characterτ0onXsuch that supτ∈Ω(X)|τ(x)|=|τ0(x)|.Thus

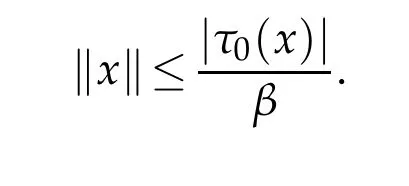
HenceEnis bounded.Moreover,PEn(x)is bounded forx∈X.Since a closed,bounded and finite dimensional subset of a normed space is compact,so by Bolzano Weierstrass theorem PEn(x)is a compact set.Similar to the proof of Theorem 3.1 we can show a contradiction under this assumption.

We denoted byCF(S)the Banach algebra of continuous functions from a topological spaceStoF,with the supremom norm.By results in[7],for eachx∈CF(S),σ(x)=x(S)and

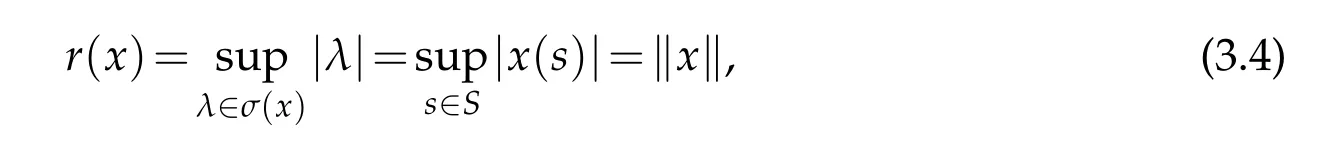
therefore ifx,y∈CF(S)and|x(s)|≤|y(s)|for eachs∈S,then kxk≤kyk.

Corollary 3.1.LetSbe a compact Hausdorff topological space.IfCF(S)is infinite dimensional thenCF(S)has a closed convex non-quasi and a closed convex non-pseudo-Chebyshev subset.

Proof.ClearlyCF(S)has property(N).By(3.4)we have inf{r(x):x∈X,kxk=1}=1>0.SinceCF(S)satisfies the conditions of Theorem3.1,will get thatCF(S)has a closed convex non-quasi-Chebyshev subset.

Also as a consequence of Theorem 3.2,we conclude thatCF(S)has a closed convex non-pseudo-Chebyshev subset.

In the following,we prove some results onC∗-algebras.This will done by using Gelfand theorem.

Theorem 3.3.LetAbe a C∗-algebra,then dim(A)=∞if and only ifAhas a bounded nonquasi-Chebyshev subset.

Proof.Ifdim(A)=∞then by a result of Ogasawara theorem(Theorem 1 in[12])A contains an infinite dimensional commutativeC∗-subalgebra B.Then by Gelfand Theorem(see[11])B≃C(Ω(A))hence as a consequence of Corollary 3.1,B has an non-quasi-Chebyshev subset This is true also for A.

For the inverse letdim(A)<∞andWbe a closed and bounded subset of A.By Bolzano Weierstrass Theorem,Wis compact.Thus for eacha∈A,PW(a)is non-empty and compact,which make a contradiction.Thusdim(A)=∞.

Theorem 3.4.LetAbe a C∗-algebra then dim(A)=∞if and only ifAhas a non-pseudo-Chebyshev subset.

Proof.The proof is similar to the that of Theorem 3.3.

Corollary 3.2.LetEbe aC∗-module over aC∗-algebra A,thendim(E)=∞ if and only ifEhas an non-quasi-Chebyshev subset.

Proof.By Lemma 2.1,Eis isometrically embedded inC∗-subalgebraB(H,K),whereH,Kare Hilbert spaces.Now,it is a consequence of Theorem 3.3.

Corollary 3.3.LetEbe aC∗-module over aC∗-algebra A thendim(E)=∞ if and only ifEhas a non-pseudo-Chebyshev subset.

Proof.It is a consequence of Theorem 3.4.

4 Characterizations of quasi-Chebyshev in C*-algebras

In this section,wegive some characterizations of best approximations and quasi-Chebyshev subalgebras inC∗-algebras.

Definition 4.1.LetAbe a Banach space andBbe a proper closed subspace ofA.An elementZ∈Ais calledB-minimal if 0 is the best approximation toZinB.

Definition 4.2.The mappingp:A→R is substate function if forh,g∈Aandα∈R+,

i)kpk=1.

ii)p(h+g)≥p(h)+p(g)andp(αh)=αp(h).

iii)pbe a positive function i.e.,p(h)≥0,forh≥0.

In Definition 4.2 ifPbe a linear function thenpis called a state.

Let A be aC∗-algebra,an elementx∈A is hermitian ifx=x∗,we denote by Ah,the set of all hermitian element of A.in fact

By the above assumptions,we have the following lemmas.

Lemma 4.1(see[13]).LetAbe a unital C∗-algebra,B a unital C∗-subalgebra ofAand a∈Ah.If a is B-minimal,then there exists a state φ ofAsuch that φ(a2)=kak2and φ(ab+b∗a)=0for all b∈B.

Letx,ybe two elements of a normed linear spaceX,thenxis orthogonal toyin the Birkhoff-James sense[2]if kxk≤kx+λyk for allλ∈C.Ifxbe Birkhoff-James orthogonal toy,we writex⊥By.LetGbe a subset ofXandx∈X.Thenxis said to be orthogonal toG(x⊥BG)wheneverx⊥Bg,∀g∈G.

Lemma 4.2(see[2]).LetAbe a C∗-algebra,a,b∈A.Then a⊥Bb if and only if there exists a state ϕ onAthat ϕ(a∗a)=kak2and ϕ(a∗b)=0.

Lemma 4.3.Let M be a subalgebra of C∗-algebraAand a∈Ah.If|PM(a)|≥1then there exist g0∈PM(a)is hermitian.

Proof.Supposem0∈PM(a),we show the real part of representationis sightly element.We have form∈M,

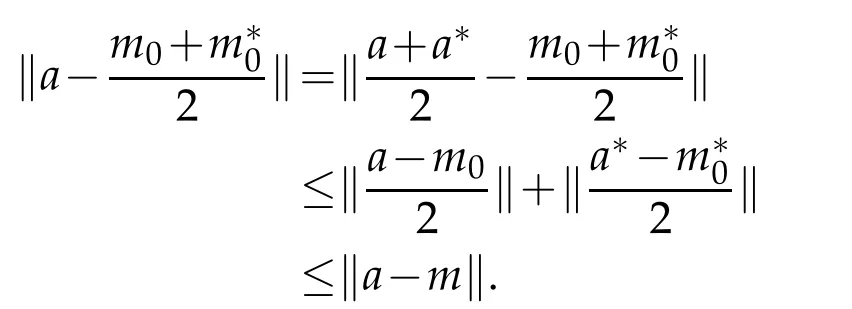
Hence

Theorem 4.1.Let M be a subalgebra ofA,m0∈M and a∈AM.Then the following statements are equivalent.

i)m0∈PM(a).

ii)There exists a substate ϕ onAsuch that for m∈M

Proof.i)→ii).Letm0∈PM(a)soa−m0⊥Bm,form∈Mthen by Lemma 4.2 there exists a stateϕmsuch thatϕm((a−m0)∗(a−m0))=ka−m0k2andϕm(m∗(a−m0))=0.

Defineϕ:A−→R,byϕ(h)=infm∈MRe ϕm(h).We showthat it is a substate.Forα∈R+andh∈A

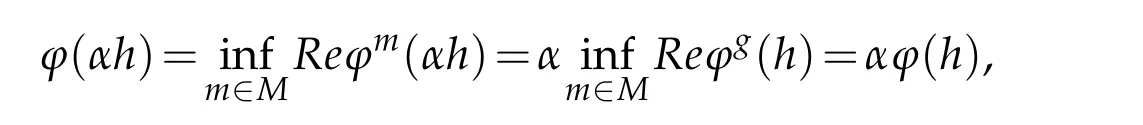
and for eachh,k∈A we have

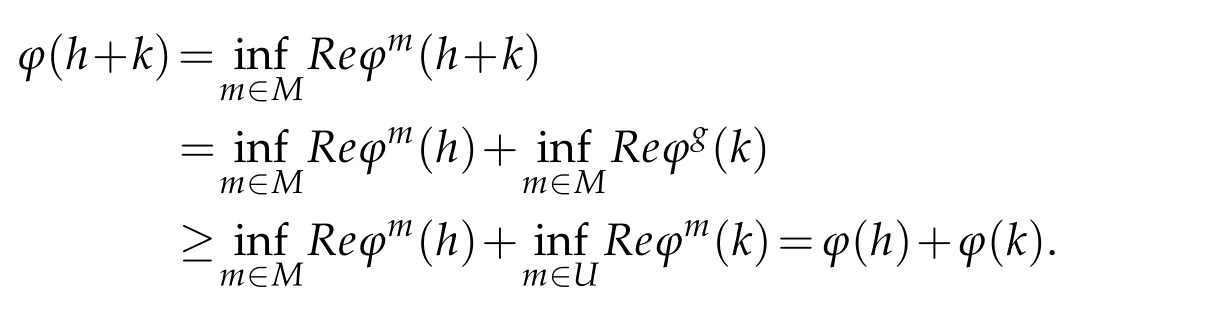
Sinceϕmis positive function and kϕmk=1=ϕm(e)(see Corollary 3.3.4[11])thenϕis positive and kϕk=1.Also

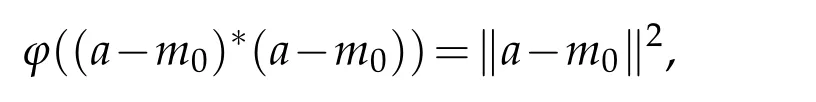
and form∈M,we have

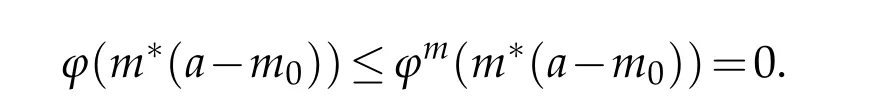
This completes the proof of this part.

ii)→i).Suppose that such a substate exists.By the Cauchy-Schwartz inequality form∈Mwe get,

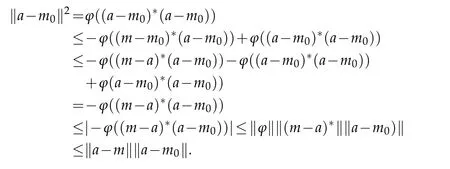
Hence ka−m0k≤ka−mk,i.e.,m0∈PM(a),which completes the proof.

Theorem 4.2.Let M be a unital proximinal*-subalgebra ofA.Then the following statements are equivalent.

i)M is a quasi-Chebyshev subalgebra.

ii)There do not exist substate ϕ onA,x0∈Aand a sequence xn∈Awithout a convergent

subsequence with x0−xn∈M(n=1,2,···)such that for m∈M,

Proof.i)⇒ii)Suppose that(ii)does not hold,then there isψon A,x0∈A and a sequencexn∈A without a convergent subsequence andx0−xn∈M,sataisfid conditions(4.3a),(4.3b).Putgn=x0−xnby Theorem 4.1,gn∈PM(x0),without a convergent subsequence,this is a contradiction.

ii)⇒i).Assume if possible thatMis not quasi-Chebyshev in A.SinceMis proximinal in A,forx∈A,PM(x)6=∅,leta∈A such thatgn∈PM(a)without a convergent subsequence.We assume thatais a hermitian element of A,also by Lemma 4.3,{gn}is hermitian(Ifa6=a∗,then we can consider the Hermitian elementin M2(A).If this element has a best approximation in M2(M)then it is easy to see that it has a best approximation in M2(M)with the formwherem∈M).By applying Lemma 4.1 there exist state functionφnsuch that

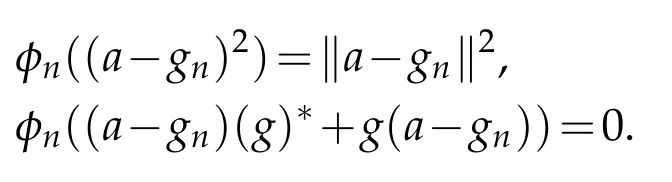
Now we defineϕ(h)=infn∈NReϕn(h),similar to the proof of the pervious theorem we can show that it is a substate.Also fori,n∈N,φn((a−gi)2)=ka−gik2because

On the other hand,we have

Henceφn((a−gi)2)=ka−gik2.Therefore forn∈N we have

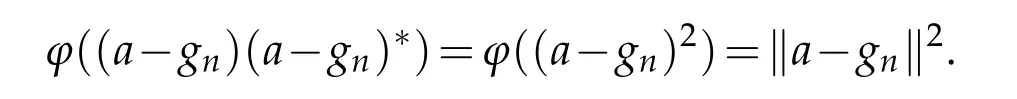
ButHence

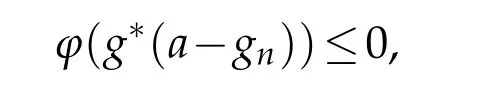
which is a contraction by part(ii).

Acknowledgements

The authors are extremely grateful to the referees for their useful comments and suggestions.

References

[1]V.S.Balaganskii,Non-proximinal sets in spaces of continuous functions,Mat.Z.,60(1996),643–657.

[2]T.Bhattacharyya and P.Grover,Chracactheriztion of birkoff-jams orthogonality,J.Math.Anal.Appl.,407(2)(2013),350–358.

[3]D.P.Blecher,A nwe approach to HilbertC-modules,Math.Annl.,307(1997),253–290.

[4]E.W.Cheney,Introduction to Approximation Theory,McGraw-Hill,New York,1966.

[5]S.Cobzas,Non-proximinal sets in Banach spaces of continuous vector-valued functions,J.Math.Anal.Appl.,261(2001),527–542.

[6]V.P.Fonf,On non-proximinal sets in spaces of continuous functions on compacta,Math.Z.,33(1983),549–558.

[7]W.Fupinwong and S.Dhompongsa,The fixed point property of unital abelian Banach algebras,Fixed Point Theory A,(2010),Article ID 362829,13 pages.

[8]L.P.Belluce and W.A.Kirk,Some fixed point theorems in metric and Banach spaces,Canad.Math.Bull.,12(1969),481–491.

[9]D.Narayana and T.S.S.R.K.Rao,Some remarks on quasi-Chebyshev subspaces,J.Math.Anal.Appl.,321(1)(2006),193–197.

[10]H.Mohebi,On quasi-Chebyshev subspaces of Banach spaces,J.Approx.Theory,107(2000),87–95.

[11]G.J.Murphy,C∗-Algebras and Operator Theory,Academic Press,Boston,Mass,USA,1990.

[12]T.Ogasawara,Finite-dimensionality of certain Banach algebras,J.Sci.Hiroshima Univ.,Ser.A,17(3)(1954),359–364.

[13]M.A.Rieffel,Leibniz seminorms and best approximation fromC∗-subalgebras,Sci.China Math.,54(11)(2011),2259–2274.

[14]J.Schauder,Der fixpunktsatz funktional raumen,Studia Math.,2(1930),171–180.

[15]I.Singer,The Theory of Best Approximation and Functional Analysis,CBMS Reg.Confer.Ser.Appl.Math.,13,Soc.Industr.App.Math.,Philadelphia,1974.