On Weighted Lp−Approximation by Weighted Bernstein-Durrmeyer Operators
2018-05-24MeilingWangDanshengYuandDejunZhao
Meiling Wang,Dansheng Yu,∗and Dejun Zhao
1Department of Mathematics,Hangzhou Normal University,Hangzhou 310036,China
2College of Fundamental Studies,Shanghai University of Engineering Science,Shanghai 201620,China
1 Introduction
Let
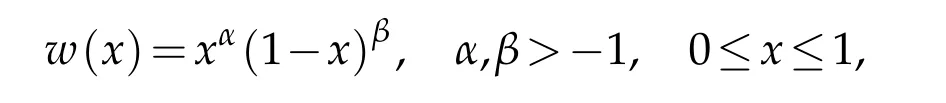
be the classical Jacobi weights.Let
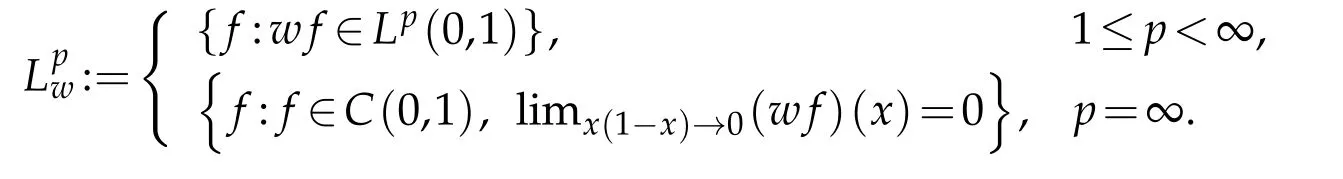
Set
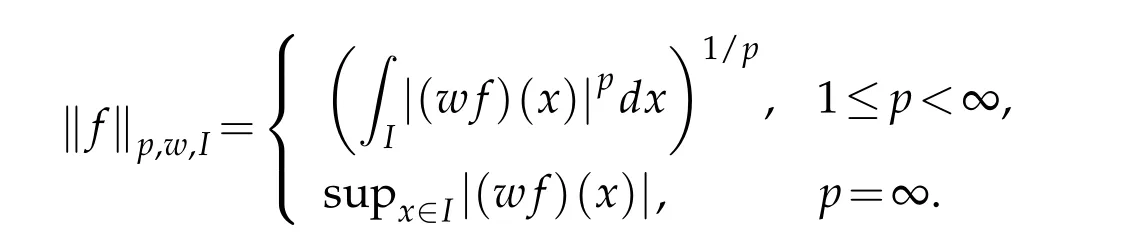
WhenI=[0,1],we briefly writekfkp,winstead ofkfkp,w,[0,1].Obviously,kfkp,wis the norm ofLpwspaces.
For anyf∈Lp([0,1]),1≤p≤∞,the corresponding Bernstein-Durrmeyer operatorsMn(f,x)are defined as follows:

where
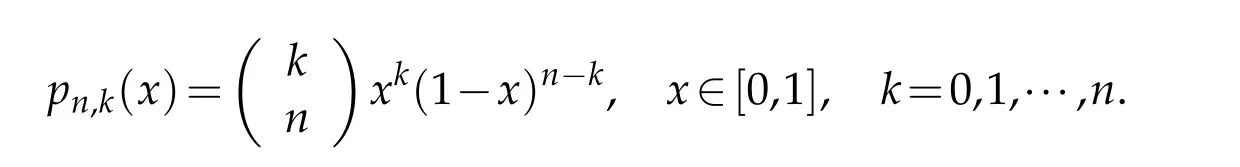
The approximation properties ofMn(f,x)inwere also studied by Zhang(see[9]).Some approximation results were given under the restrictions
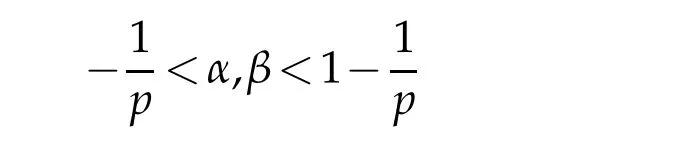
on the weight parameters.Generally speaking,the restrictions can not be eliminated for the approximation byMn(f,x).For the weighted approximation by Kantorovich-Bernstein operators defined by
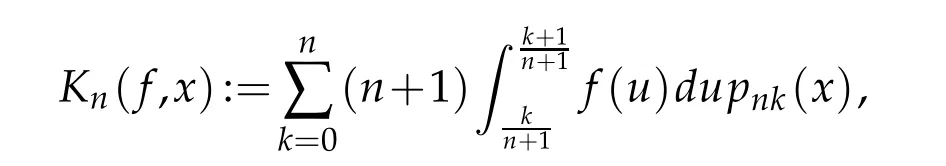
the situation is similar(see[5]).Recently,Della Vecchia,Mastroianni and Szabados(see[2])introduced a weighted generalization of theKn(f,x)as follows:
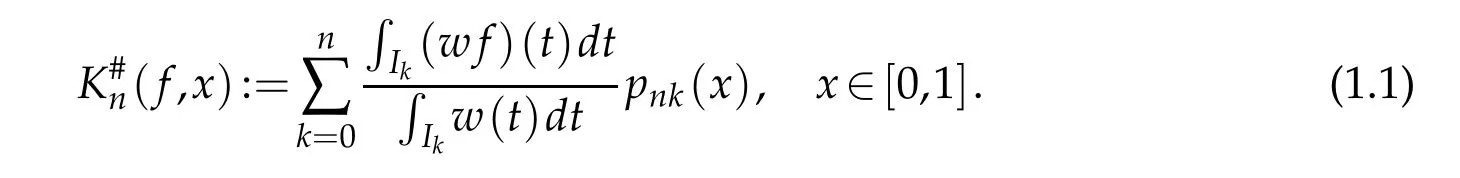
Whenα=β=0,K#n(f,x)reduces to the classical Kantorovich-Bernstein operatorKn(f,x).Della Vecchia,Mastroianni and Szabados obtained the direct and converse theorems and a Voronovskaya-type relation in[2],and solved the saturation problem of the operator in[3].Their results showed thatf,x)allows a wider class of functions than the operatorKn(f,x).In fact,they dropped the restrictionsα,β<1−on the weight parameters.Later,Yu(see[8])introduced another kind of modified Bernstein-Kantorvich operators,and established direct and converse results on weighted approximation which also have no restrictionsα,β<1−
Then,a natural question is:can we modified the Bernstein-Durrmeyer operators properly such that the restrictionsα,β<1−onweighted approximation can be dropped?In the present paper,we will show that the weighted Bernstein-Durrmeyer operator introduced by Berens and Xu(see[1])is the one we need.The weighted Bernstein-Durrmeyer operator is defined as follows:
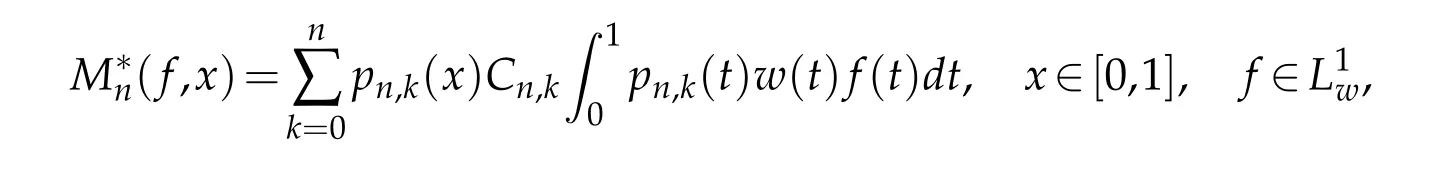
where
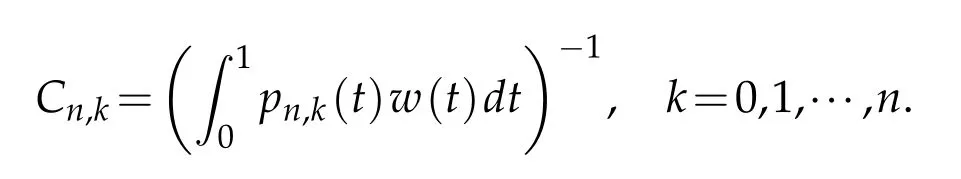
Define
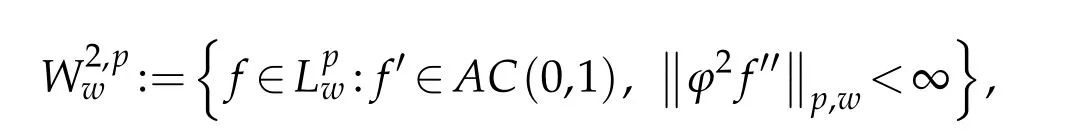
whereϕ(x)=pandAC(I)is the set of all absolutely continuous functions onI.Forf∈define the weighted modulus of smoothness by
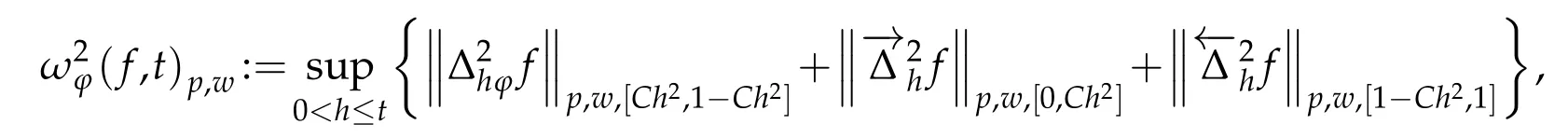
with
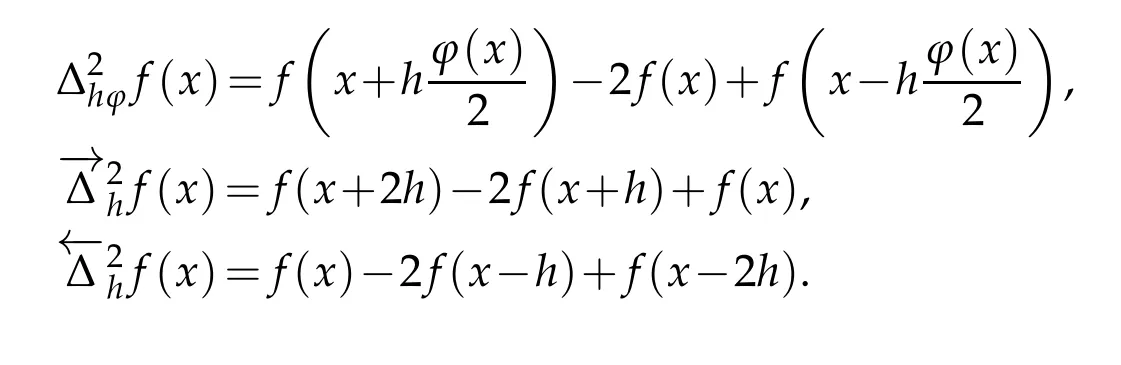
Define
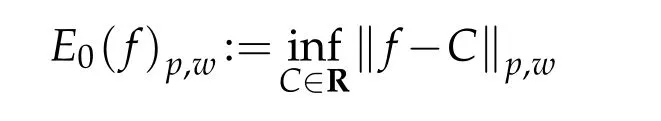
to be the best approximation offin weightedspaces by constants.
The main results of the present paper are the following:
Theorem 1.1.If f∈Lpw,1≤p≤∞,then
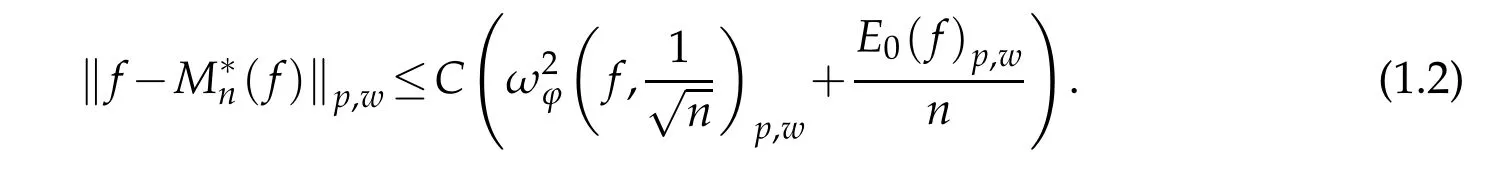
Theorem 1.2.If f∈Lpw,1≤p≤∞,then
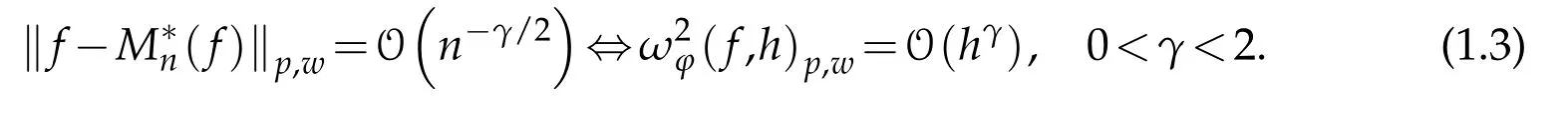
2 Auxiliary lemmas
We need the following inequalities:
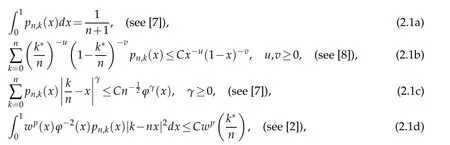
where
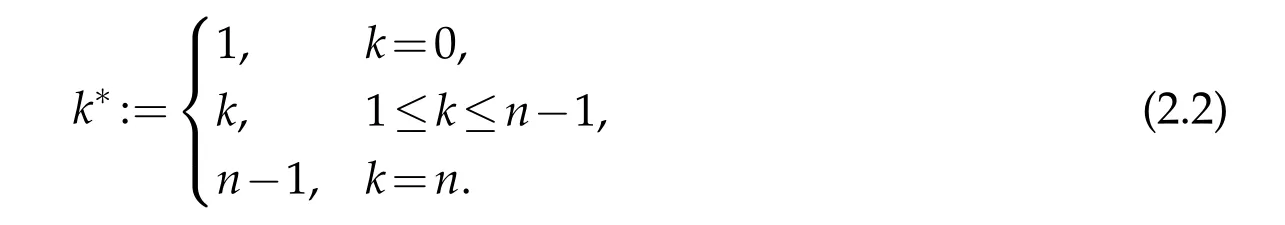
It should be noted that(2.1d)is contained in the first inequality of[2,pp.9].
Lemma 2.1.For1≤p<∞,0≤k≤n and n≥3,we have
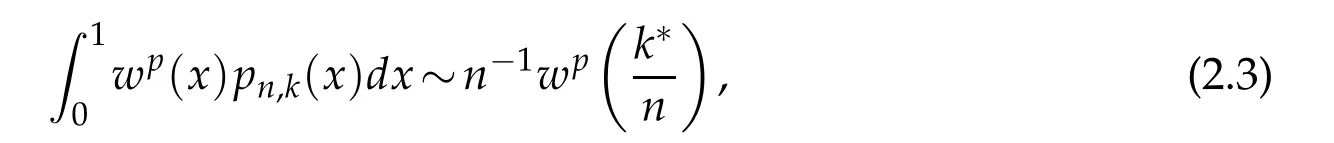
where k∗is defined by(2.2).
Proof.By the fact that(see[3])
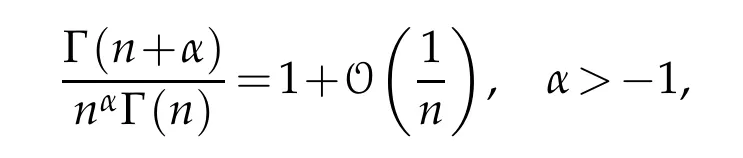
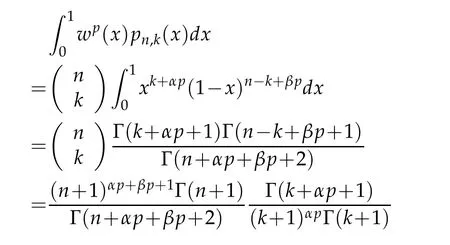
we deduce that
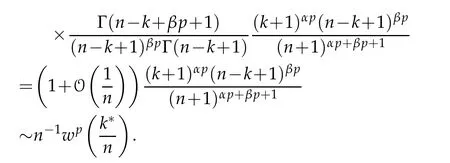
Thus,we complete the proof.
Especially,by takingp=1 in(2.3),we get
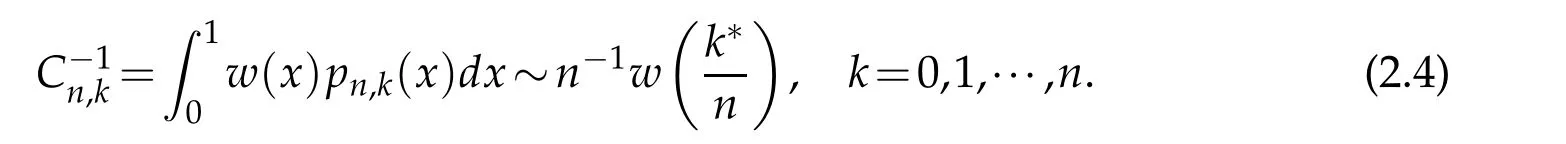
Lemma 2.2.For any f∈,1≤p≤∞,we have
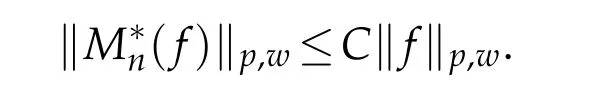
Proof.Whenp=∞,by(2.1a),(2.4)and(2.1b),we get
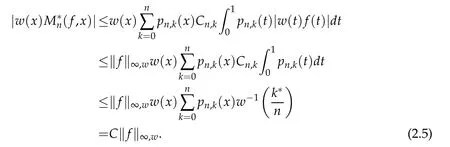
When 1 By a similar and more simpler deduction,we see that(2.6)also holds forp=1. Combining(2.5)and(2.6),Lemma 2.2 is proved. Lemma 2.3.If f∈,then Proof.Direct calculations yield that(see[4,pp.331-332]), Therefore, Forp=∞,by(2.1a),(2.1b)and(2.1c),we have For 1 We finish Lemma 2.3 by combining(2.8)and(2.9). Lemma 2.4.If f∈,then Proof.We prove the result by estimating the integral on two intervalsandEnrespectively. Simple calculation leads to ForI1(n,x),whenp=∞,by applying(2.1a)-(2.1c),(2.4)and Cauchy’s inequality,we have When 1≤p<∞,by using Hlder’s inequality twice forp>1(p=1 is more direct),(2.1c),(2.1d),(2.4)and(2.1a), ForI2(n,x),by Lemma 2.2,we have ForI3(n,x),whenp=∞,by(2.1a)-(2.1d)and(2.4),we have where in the last inequality,we used the fact 1/ϕ(x)≤C,x∈En. When 1≤p<∞,by using Hlder’s inequality,(2.1a),(2.1c),(2.1d),(2.4),and the fact 1/ϕ(x)≤C,x∈Enagain,we deduce that By combining(2.10)-(2.15),we already have Now,we estimate the integral onBy(2.7),we have When 1≤p<∞,noting thatnϕ2(x)≤Cforx∈Ecn,by Hlder’s inequality,(2.3)and(2.4),we have Whenp=∞,forx∈Ecn,by(2.1a)and(2.1b), By(2.18)and(2.19),we see that By(2.17)and(2.20),we complete the proof of Lemma 2.4. Lemma 2.5.For any nonnegative integer m,set Then and where pi,m,n,α,β(x)are polynomials in x of fixed degree with coefficients that are bounded uniformly for all n. Proof.Analogue to[4],we have the recursion relation: Direct calculations yield that and where By(2.23)-(2.25)and a simple induction process,we obtain(2.21)and(2.22). By(2.21),we have Lemma 2.6.For any given m,it holds that Lemma 2.7.For1≤p<∞,f∈W2,pw,there is a positive constant C such that where Proof.Firstly,we consider the casep=1.Setg(v)=w(v)ϕ2(v)f′(v).By the inequality(see[5]): we have Set Forl≥1,by(2.1b),(2.4),and(2.26)withw≡1,we deduce that Forl=0,by(2.1b)and(2.4), Therefore, Noting thatwe have Since(see[5]) then(by takingh=(l+1)) Therefore, Thus,we can conclude that Now,we begin to prove the following Forl≥1,by(2.4),and(2.26),we deduce that Forl=0,by(2.1b),(2.3)and(2.4),we have Then,we can derive(2.30)in a similar way to the proof of(2.29). By combining(2.28)-(2.30),we obtain Lemma 2.7 forp=1. Finally,we prove Lemma 2.7 for 1 Set The following maximal function inequality are well known Since 1/w(v)≤C(1/w(t)+1/w(x))for anyvbetweenxandt,by the maximal function inequality,we have Therefore,we only need to prove that where kKk∞,Enis the usual supremum norm ofKonEn,and For the first part ofK,by(2.26), For the second part ofK,by(2.4),(2.1b)and(2.26)(withw=1), By(2.33)and(2.34),we get(2.31),and thus Lemma 2.7 is valid for 1 Proofof Theorem 1.1.It is sufficient to prove that forϕ2f′′∈.By the Taylor’s formula we have Then,by(2.25)and(2.27),we get(3.1)immediately. ? Proofof Theorem 1.2.The”⇐=”part follows from Theorem 1.1.The”=⇒”part can be done by using the argument of proof of Theorem 9.3.2 in[5],we omit the details here.? References [1]H.Berens and Y.Xu,On Bernstein-Durrmeyer polynomials with Jacobi weights,In C.K.Chui,editor,Approximation Theory and Functional Analysis,Boston:Academic Press,(1991),25–46. [2]B.Della Vecchia,G.Mastroianni and J.Szabados,A weighted generalization of the classical Kantorovich operator,Rend.Circ.Mat.Palermo,82(2)(2010),1–27. [3]B.Della Vecchia,G.Mastroianni and J.Szabados,A weighted generalization of the classical Kantorovich operator,II:Saturation,Mediter.J.Math.,10(2013),1–15. [4]M.M.Derriennic.Sur l’approximation de fonctions integrables sur[0,1]par des ploynomes de Bernstein modifies,J.Approx.Theory,31(1981),325–343. [5]Z.Ditzian,V.Totik,Moduli of Smoothness,Berlin:Springer-Verlag,1987. [6]J.L.Durrmeyer,une formule d’inversion de la transformee de Laplace:Applications a la therie des moments,These de 3e cycle,Faculte des sciences de l’universitede Paris,1967. [7]G.G.Lorentz,Bernstein Polynomials,University of Toronto Press,Toronto,1953. [8]D.S.Yu,Weighted approximation by modified Kantorovich-Bernstein operators,ActaMath.Hungar.,141(2013),132–149. [9]Z.Q.Zhang,On weighted approximation by Bernstein-Durrmeyer operators,Approx.Theory Appl.,7(1991),51–64.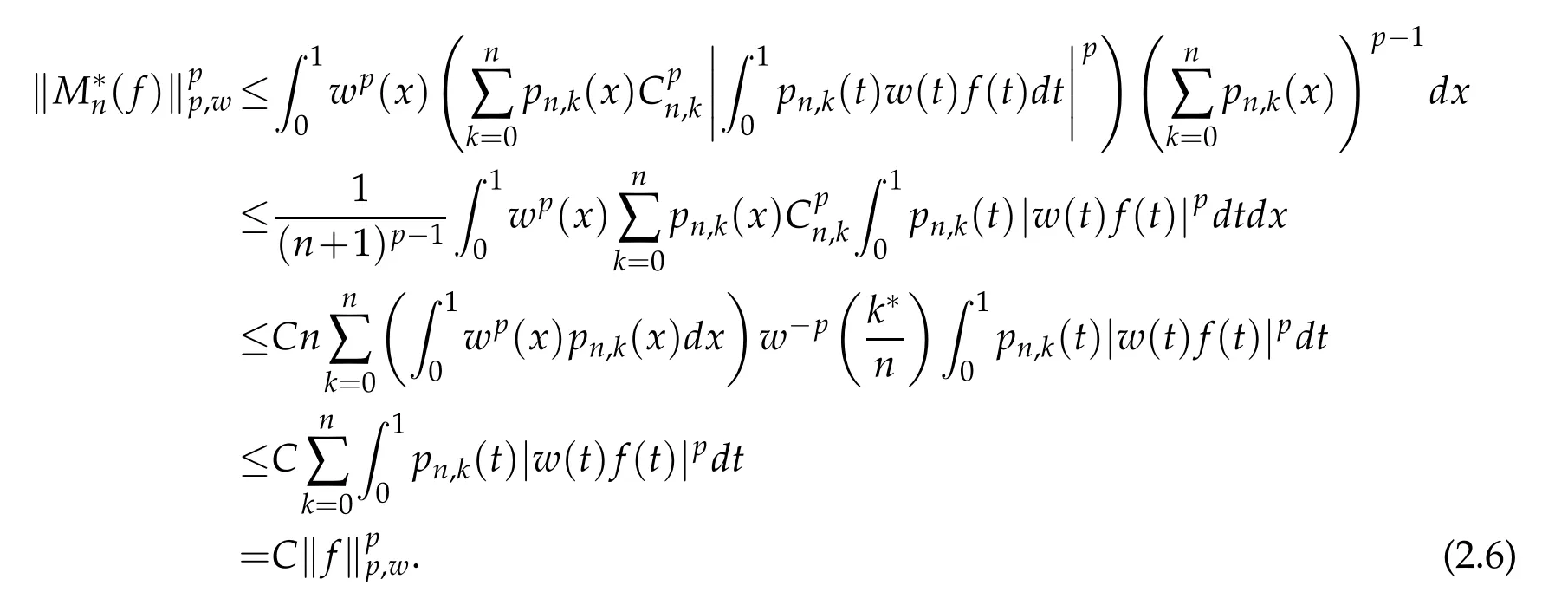

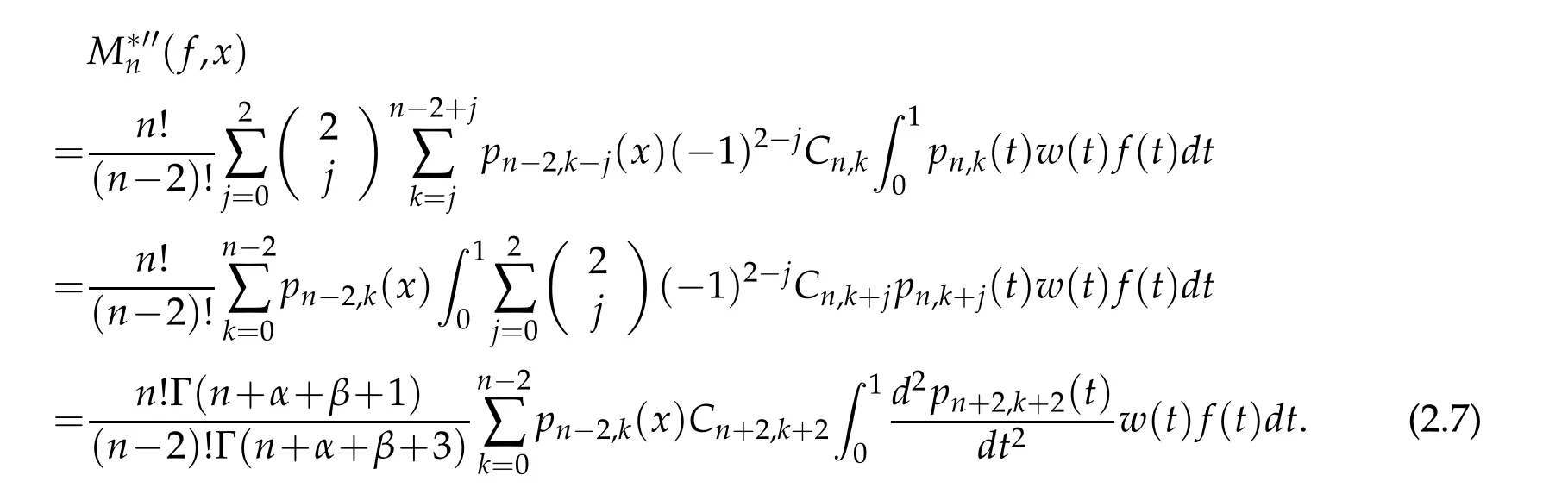
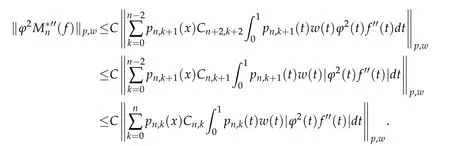


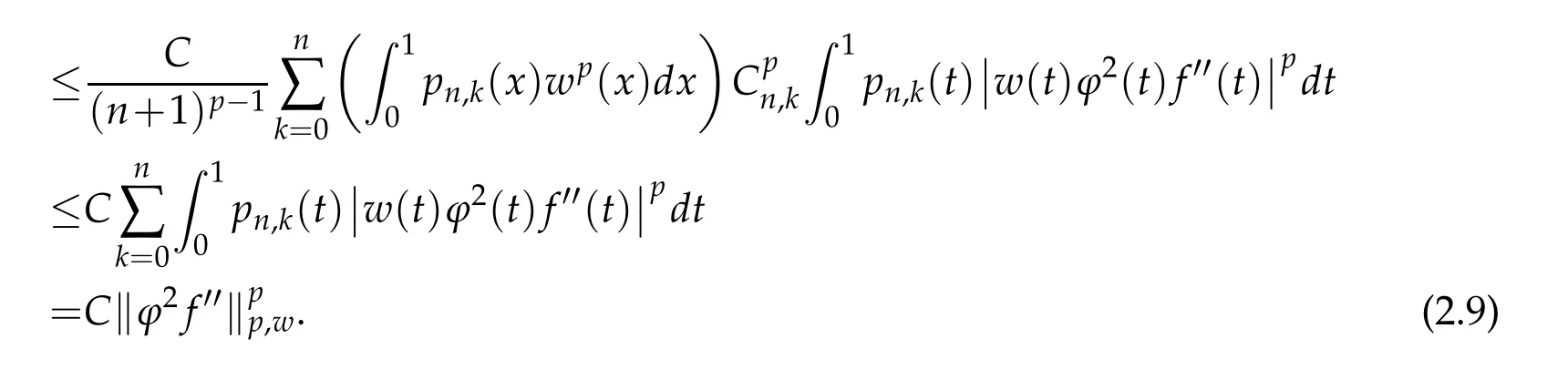
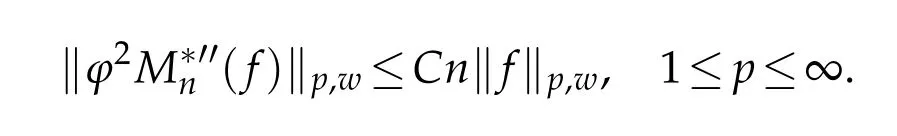
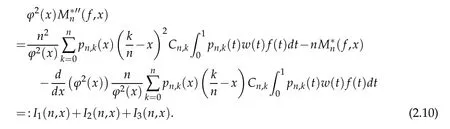
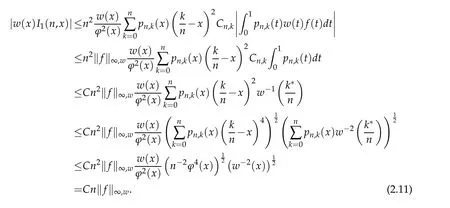
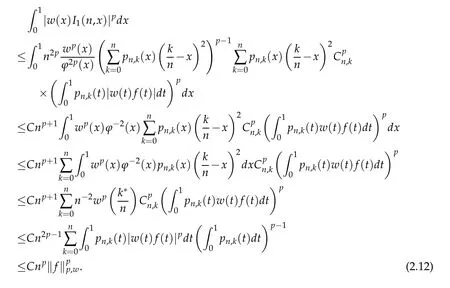
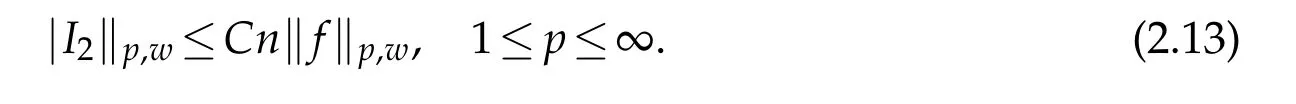
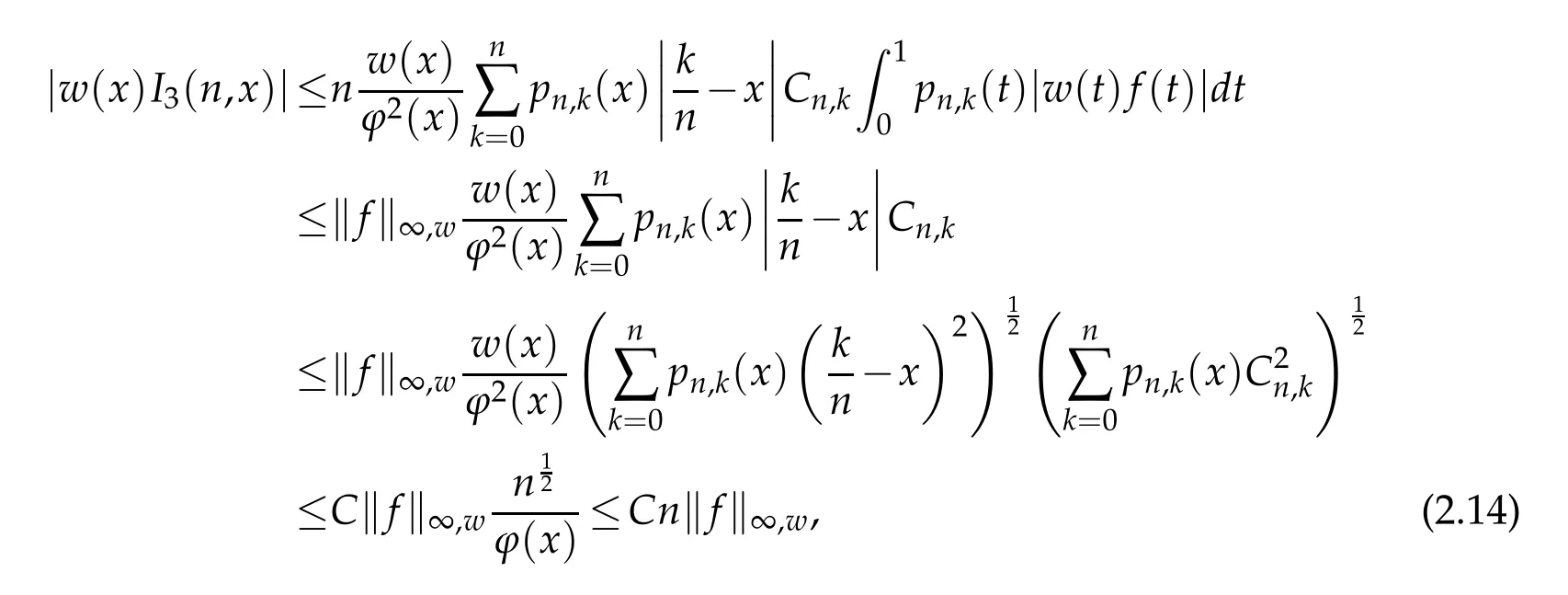

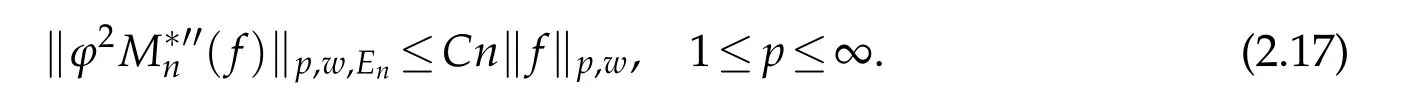
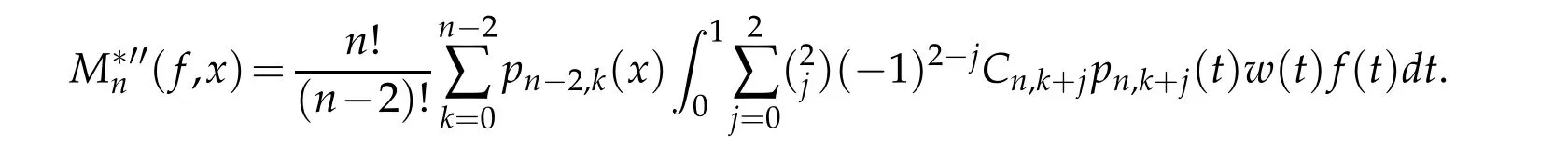

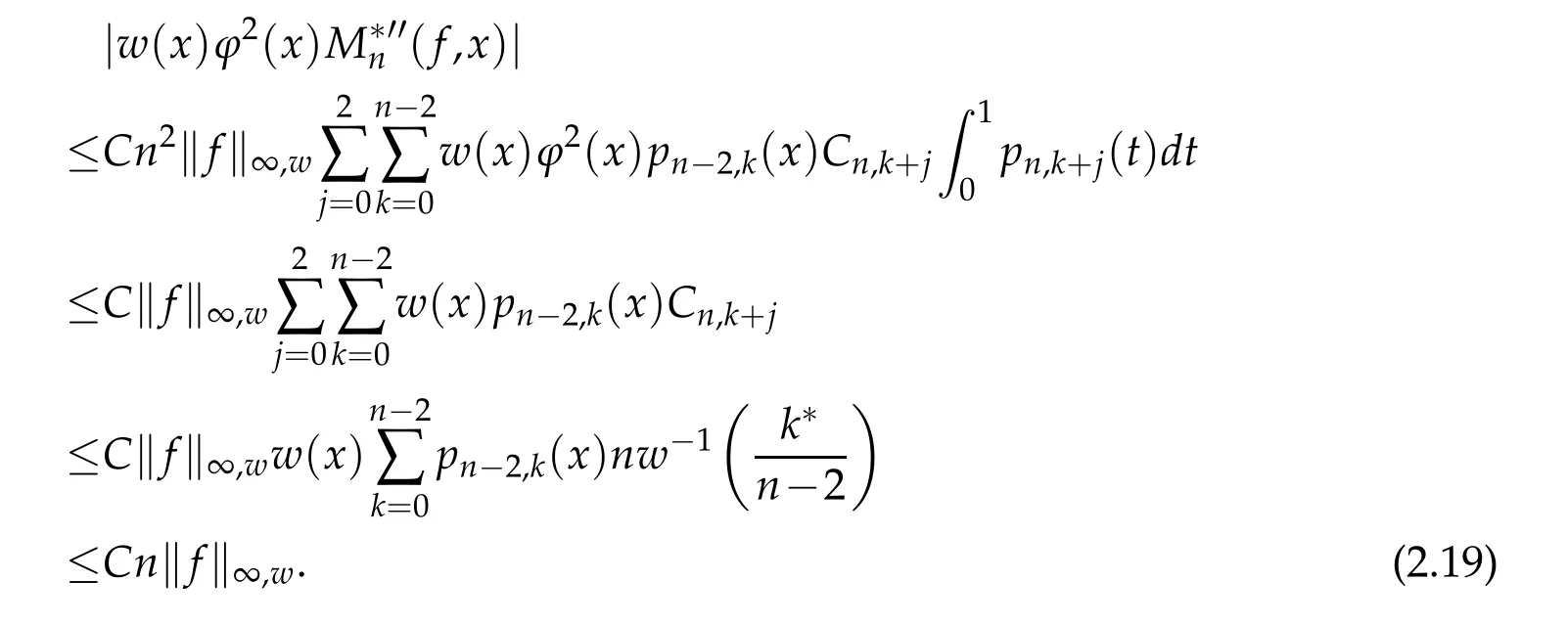
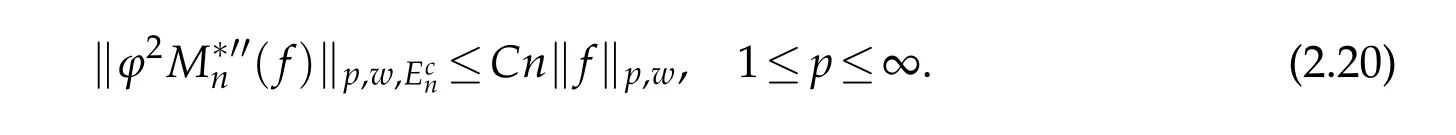
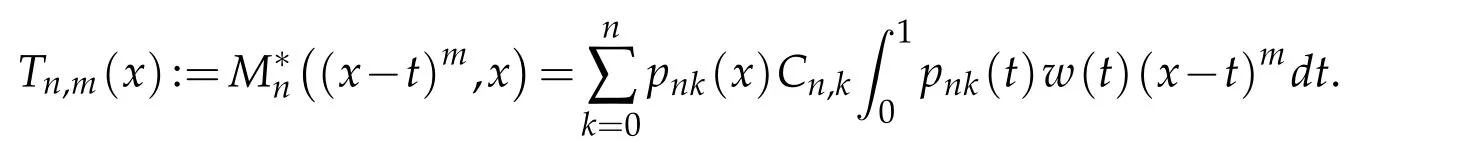
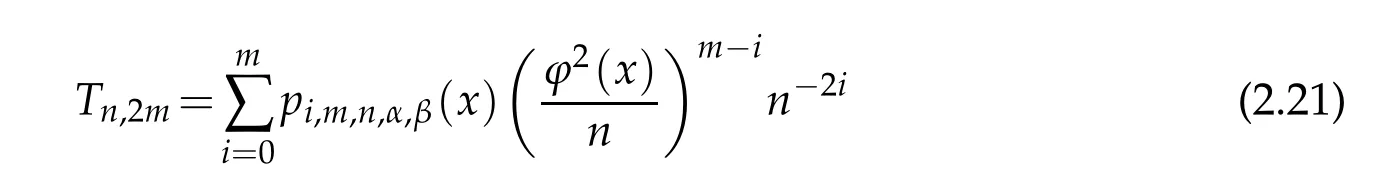
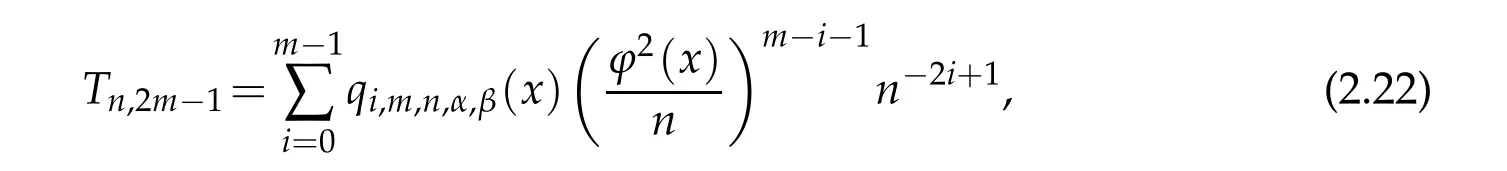
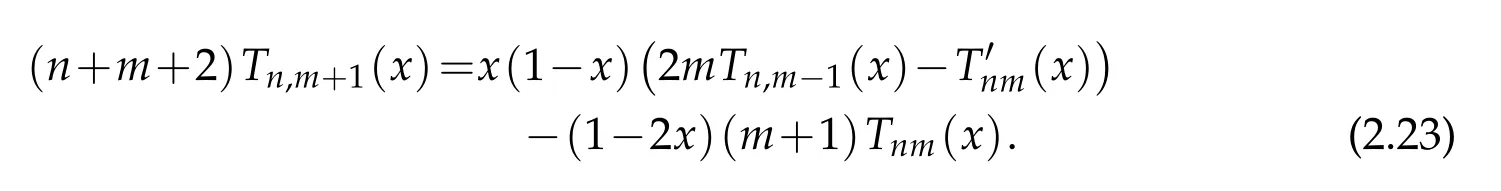


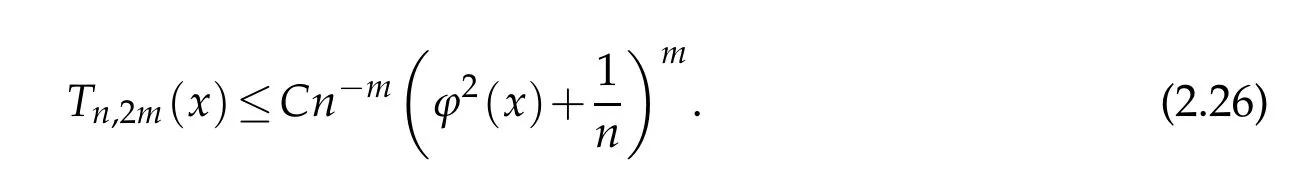
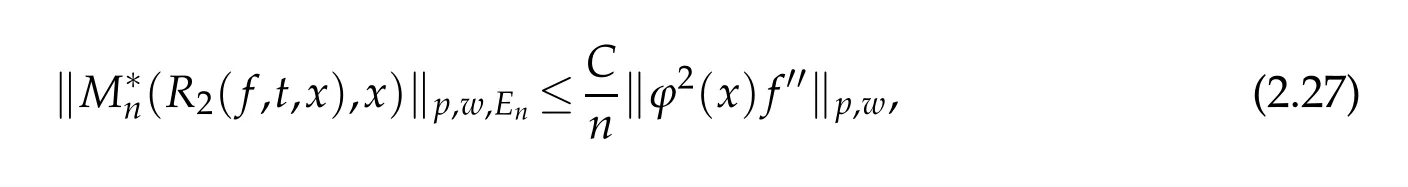
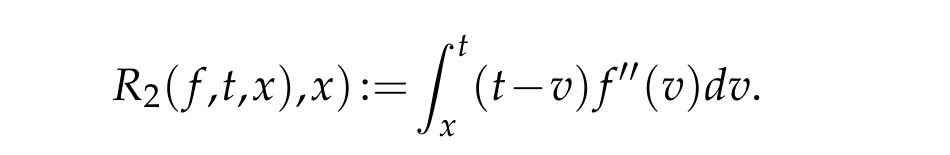
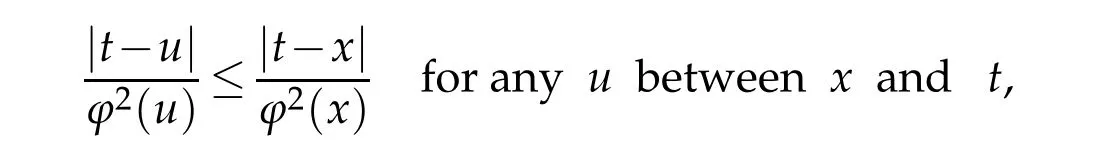
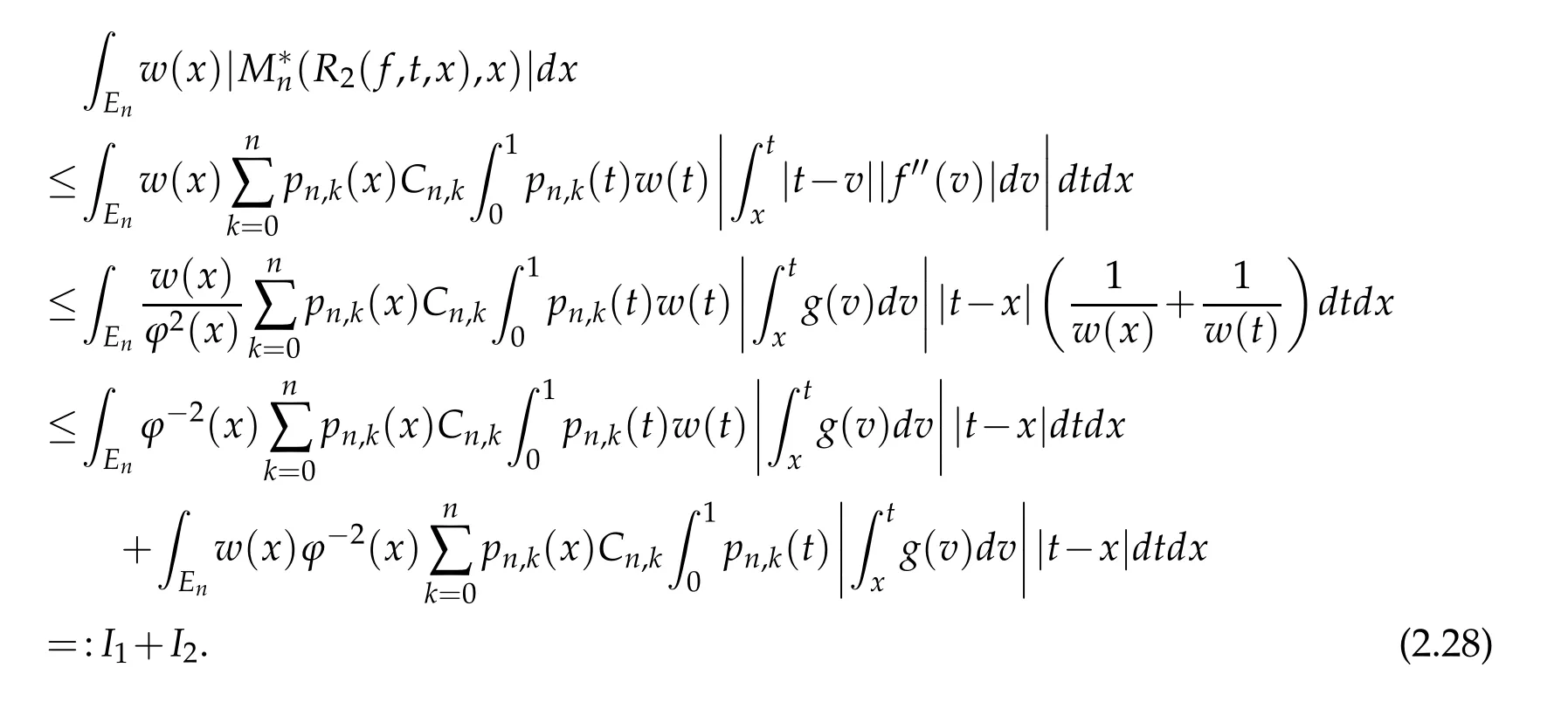
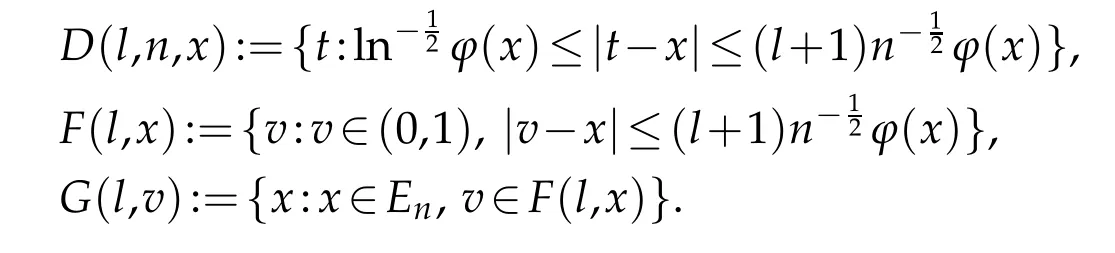
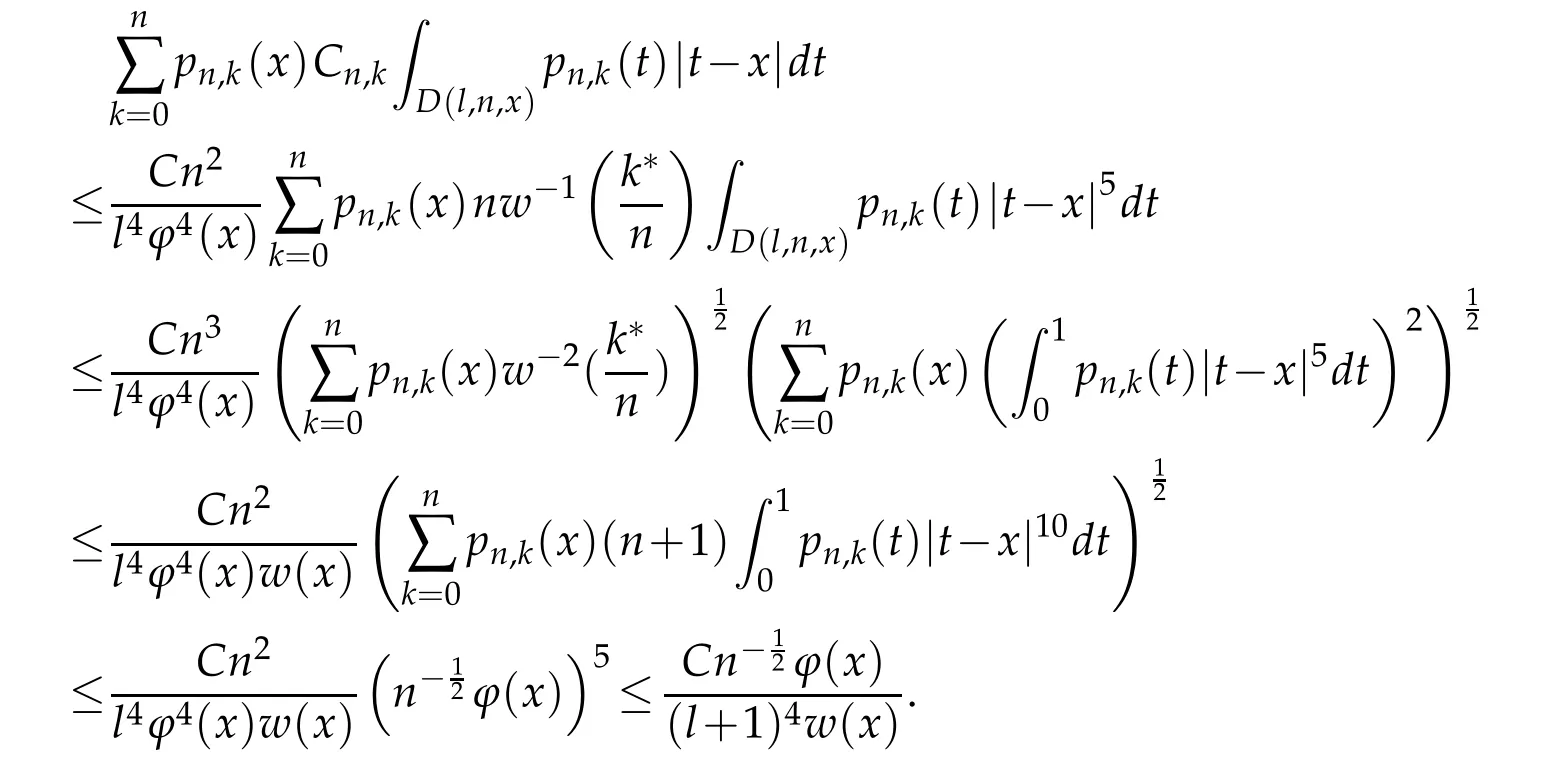
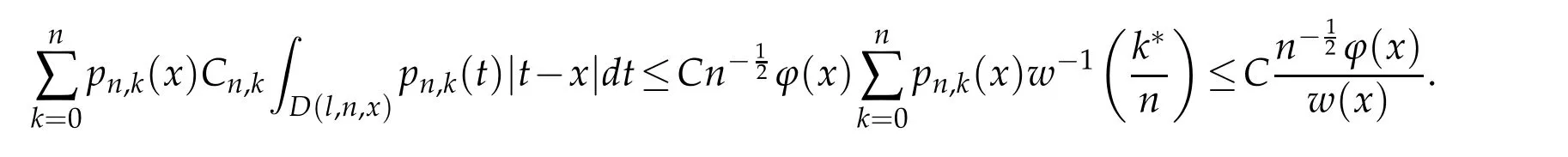
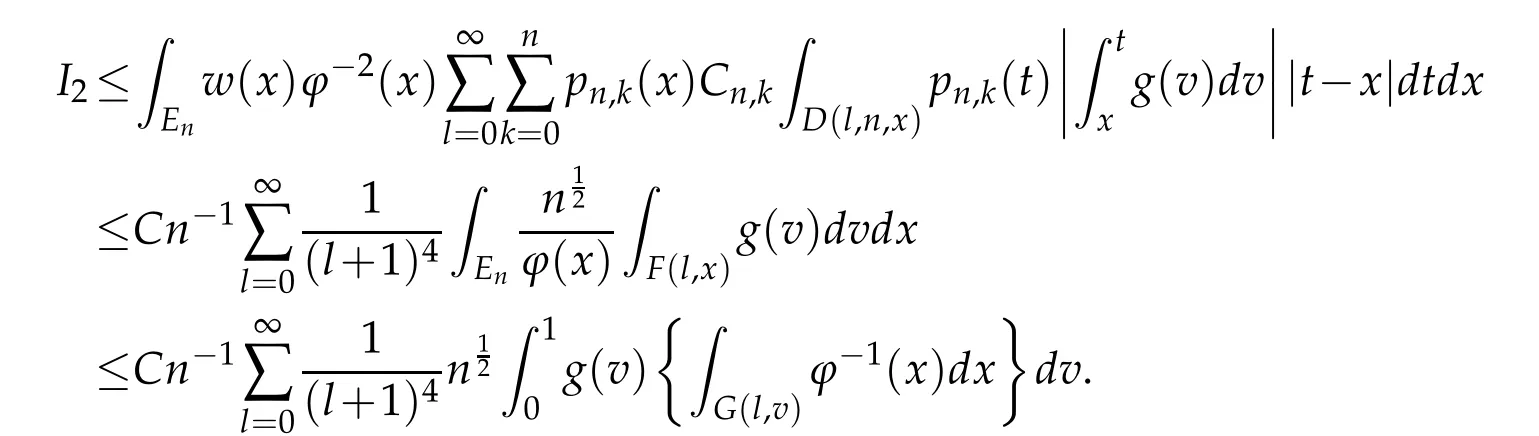
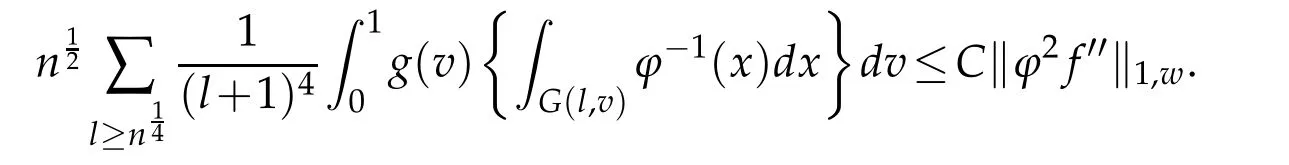
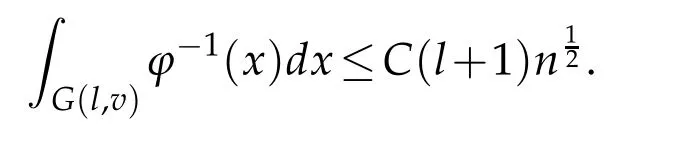
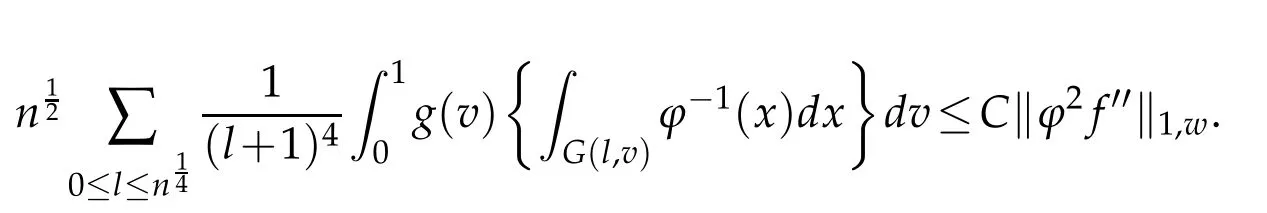


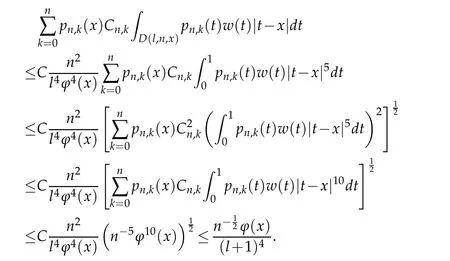
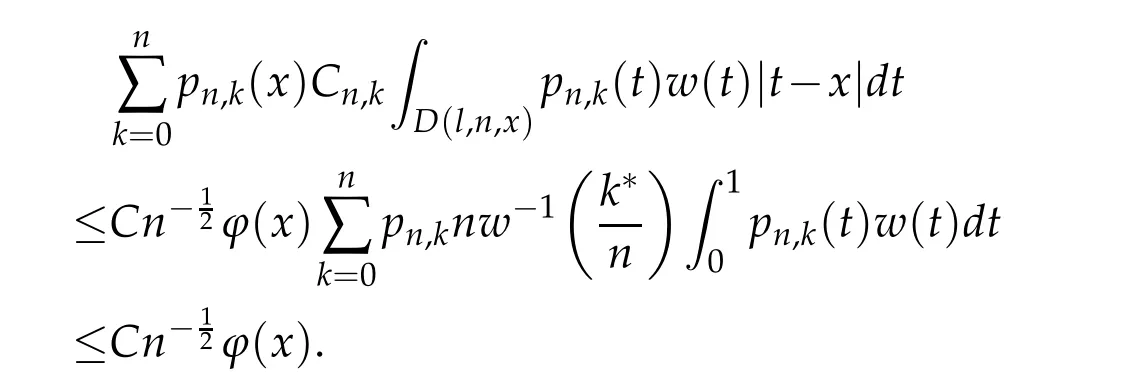
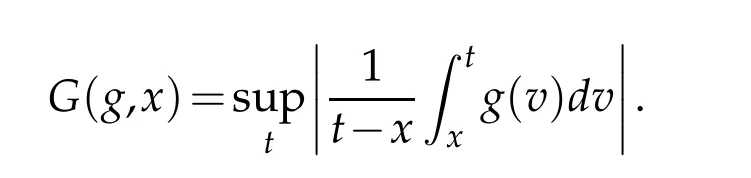

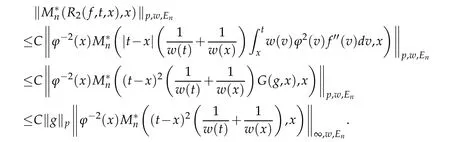
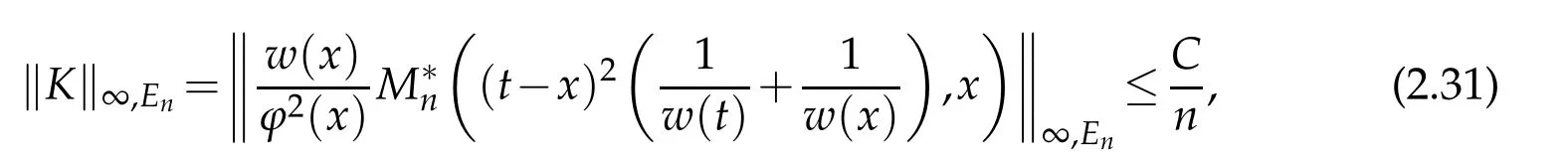
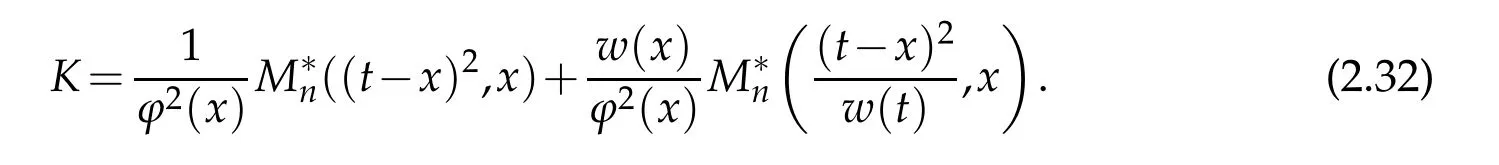
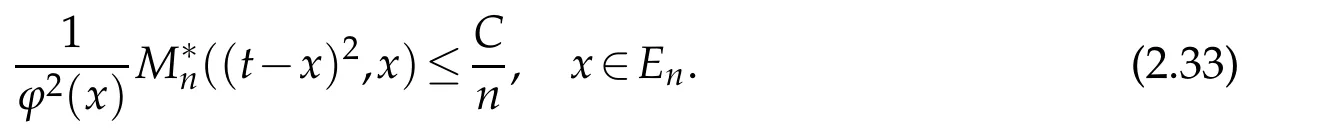

3 Proofs of theorems

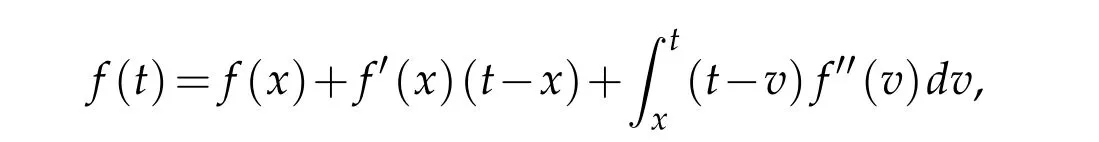
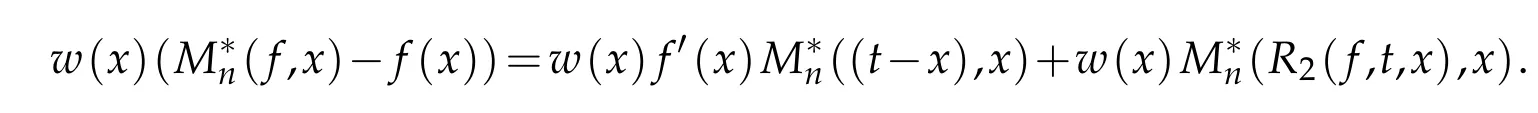
杂志排行
Analysis in Theory and Applications的其它文章
- A Struwe Type Decomposition Result for a Singular Elliptic Equation on Compact Riemannian Manifolds
- On an Axiomatic about Functional Means
- Commutators of Singular Integral Operators Related to Magnetic Schrdinger Operators
- Some Generalized q-Bessel Type Wavelets and Associated Transforms
- Approximation for Certain Stancu Type Summation Integral Operator
- On Quasi-Chebyshevity Subsets of Unital Banach Algebras
