Approximation for Certain Stancu Type Summation Integral Operator

Prerna Maheshwari

Department of Mathematics,SRM University Delhi-NCR Campus,Modinagar(UP),India

1 Introduction

H.M.Srivastava and V.Gupta[15],proposed a certain family of linear positive operators defined as

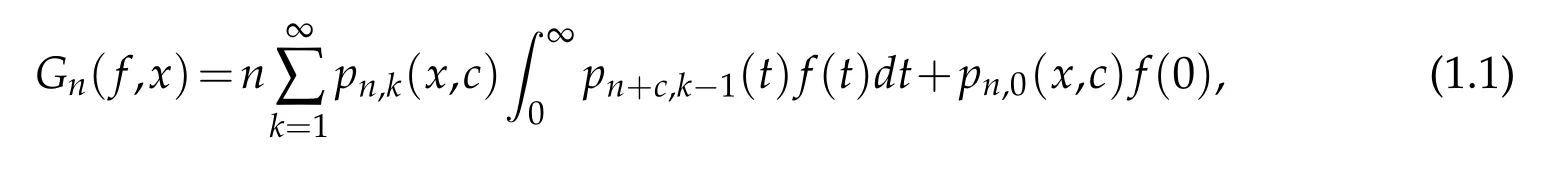
x∈[0,∞),where

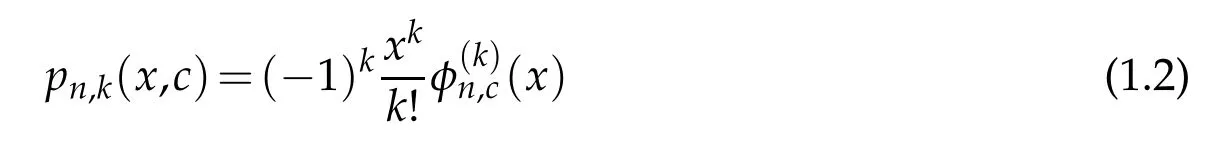
and

• forc=0,φn(x)=e−nx,we obtain Phillips operators,

• forc∈N,φn(x)=(1+cx)−n c,we get the discretely defined Baskakov-Durrmeyer operators.

The sequence{φn}n∈Nof the function defined on an interval[0,b],b>0 satisfies the following properties for everyn∈N,k∈N0,

1.φn,c∈C∞([a,b]),

2.φn,c(0)=1,

3.φn,cis completely monotone i.e.,(−1)

4.There exist an integercsuch that

Remark 1.1.Functionsφn,chave many applications in different fields of Science and Mathematics like potential theory,probability theory,Physics and Numerical Analysis.A collection of most interesting properties of such functions can be found in[17].

These operators are also termed as Srivastava-Gupta operators(see[2,10,16]).In[7],authors have considered the Bezier variant of these operators and estimated the rate of convergence for functions of bounded variation.Motivated by the sequenceGn,Gupta et al.[4]also defined a mixed family of summation integral operators with different weight function.In approximation theory the genuine type of operators are very important,as they are defined implicitly with values of functions at end points of the interval in which the operators are defined.In 1954,Phillips[14]introduced such operators and later Mazhar and Totik[8]discussed these operators in different form.

In[5,11,12]authors have also studied in this direction and discussed different approximation properties of various operators.

Based on two parametersα,βand satisfying the condition 0≤α≤β,motivated by the recent work on Stancu type of generalization(see[1,9,13])in the present paper,we consider the Stancu type generalization of operators(1.1)as

wherepn,v(x,c)is defined above in(1.2).In this paper,we study simultaneous approximation for the casec=1 of the operators defined in(1.3)and establish Voronovskaja type asymptotic formula and error estimation.To obtain moments by using hypergeometric series,we use the technique developed by[6].

2 Alternate forms

The operatorsfor the casec=1 can be written as below.Forx∈[0,∞)

where the kernel

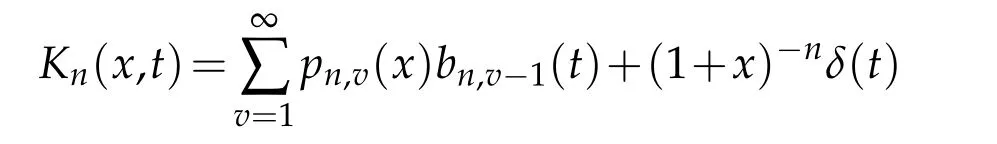
withδ(t)is Dirac delta function andpn,v(x)andbn,v(t)are Baskakov and Beta basis functions and are defined as

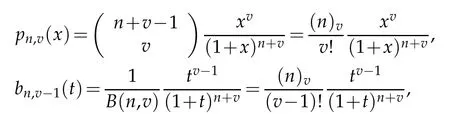
where the Pochhammer symbol(n)vis defined as

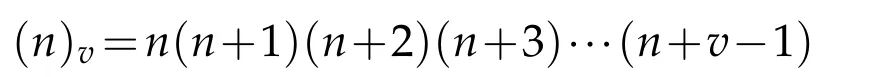
andB(n,v)are Beta functions.The operators(2.1b)can be written as

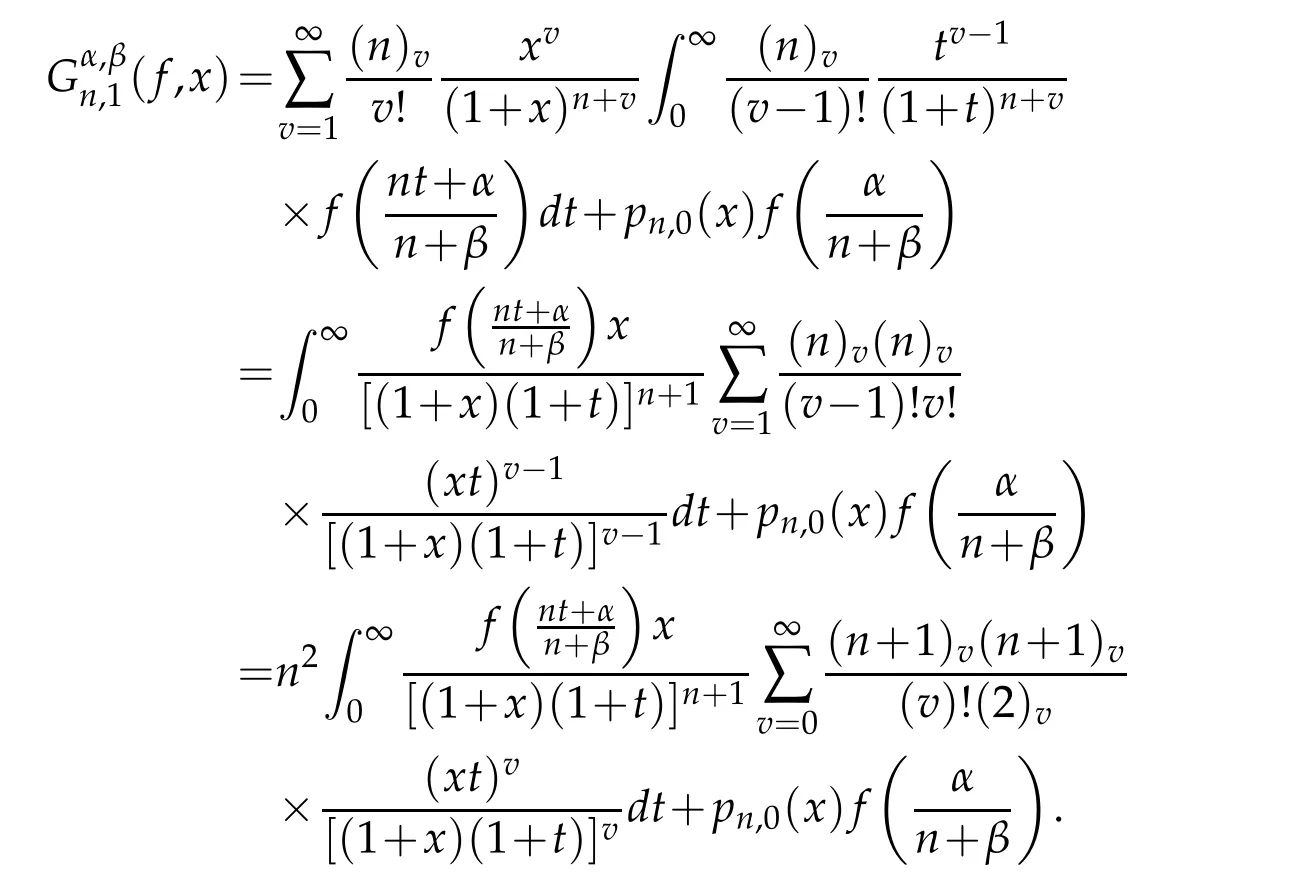
Using the hypergeometric series properties

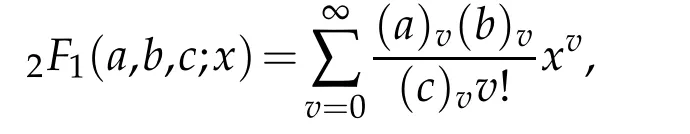
we have

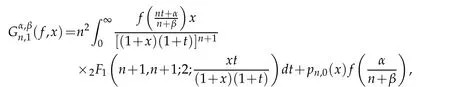
on applying Pfaff-Kummar transformation

we get

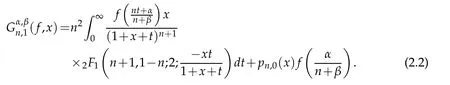
This is the alternate form of the operators(2.1b)in terms of hypergeometric function.

3 Auxiliary results

In this section,we present some lemmas,which will be useful for the proof of main theorem.

Lemma 3.1.For n>0and r≥1,we have

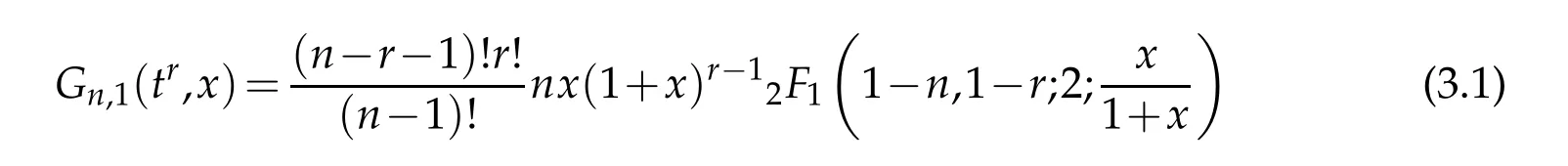
and

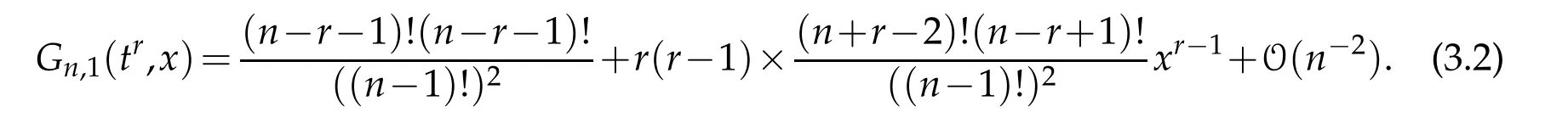
Proof.Takingf(t)=tr,using the transformationt=(1+x)zand applying Pfaff-Kummar transformation,we get

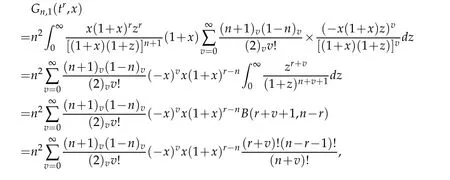
using(n+v)!=n!(n+1)v,we get

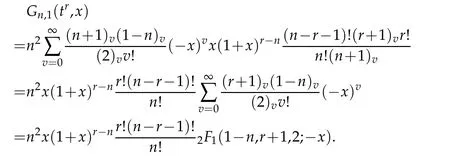
Thus,we complete the proof.

Now using

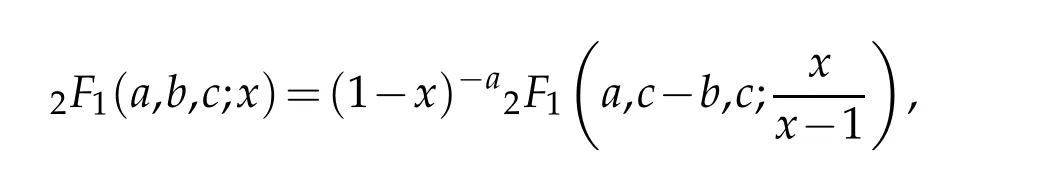
we have

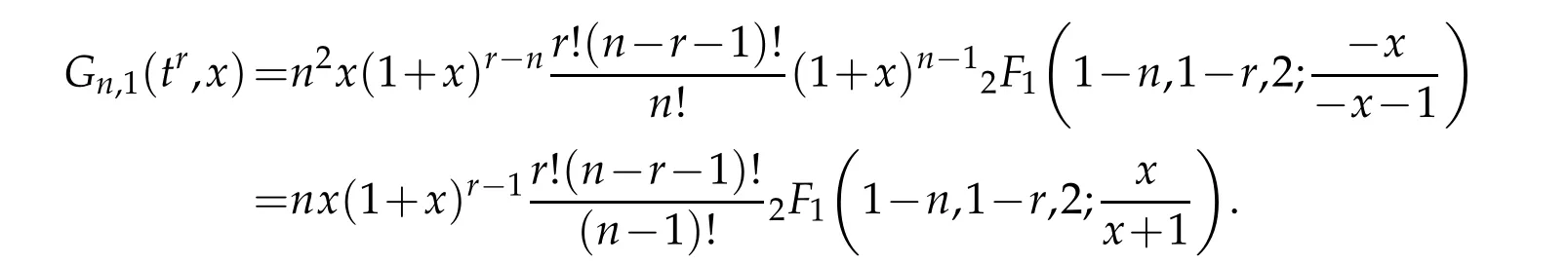
Lemma 3.2.For0≤α≤β,we have

Proof.The relation between the operators(1.1)and the operators(2.2)can be defined as

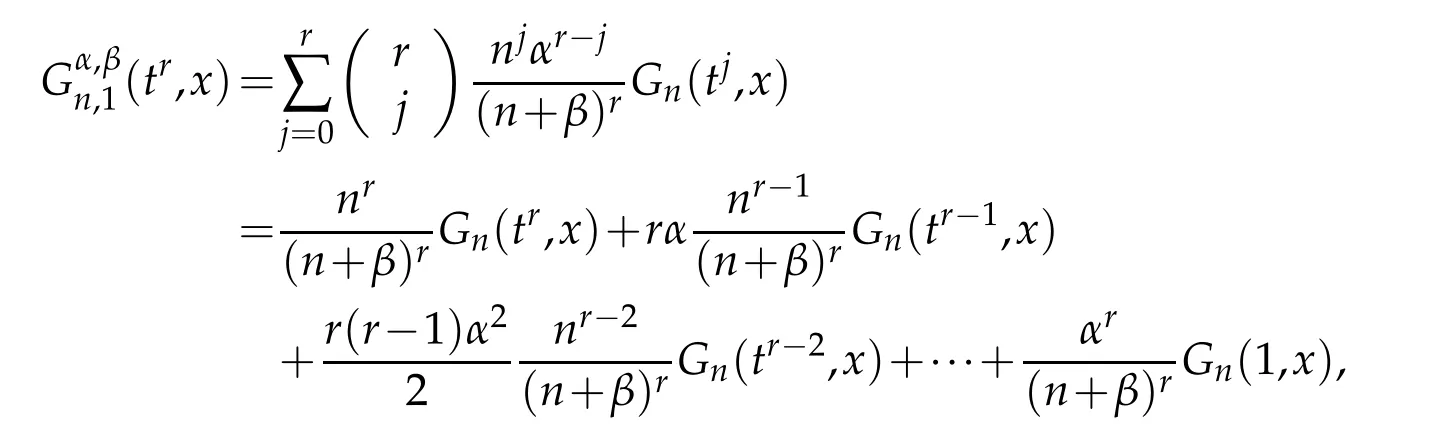
by applying(3.2),we get the required result.

Lemma 3.3(see[3]).Let m∈N∪{0}and

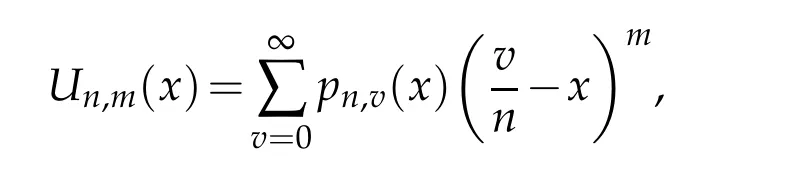
then Un,0(x)=1,Un,1(x)=0and there holds the recurrence relation

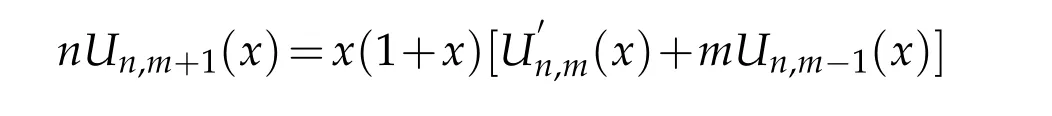
and Uwhere[α]being the integral part of α.

Lemma 3.4.For m∈N∪{0},we define the central moments as

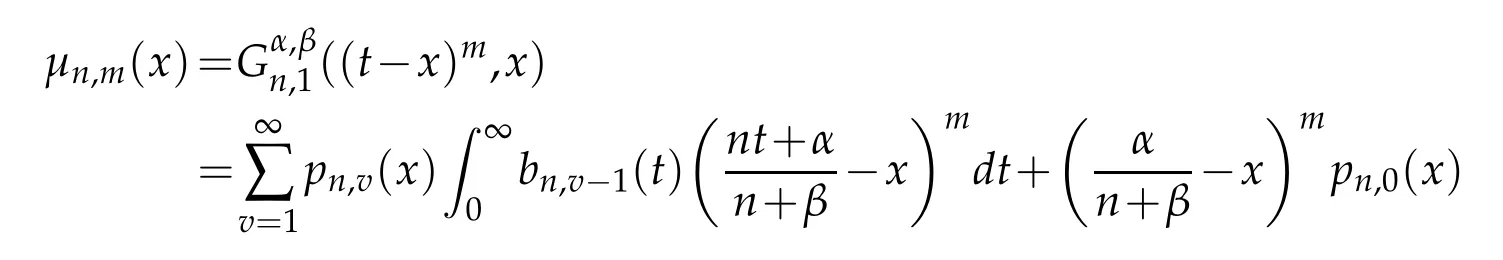
for n>(m+1),following recurrence relation holds

here

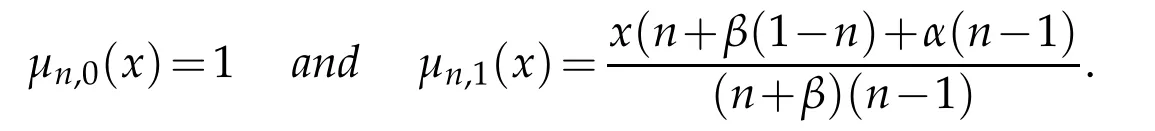
Consequently for each x∈[0,∞),we have from above recurrence relation that

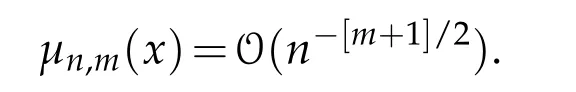
Proof.The values ofµn,0(x)andµn,1(x)easily follow from the definition of operators(2.1a).To prove the recurrence relation,we apply the following identities

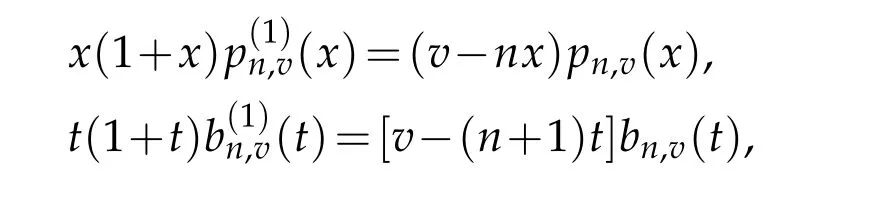
we get

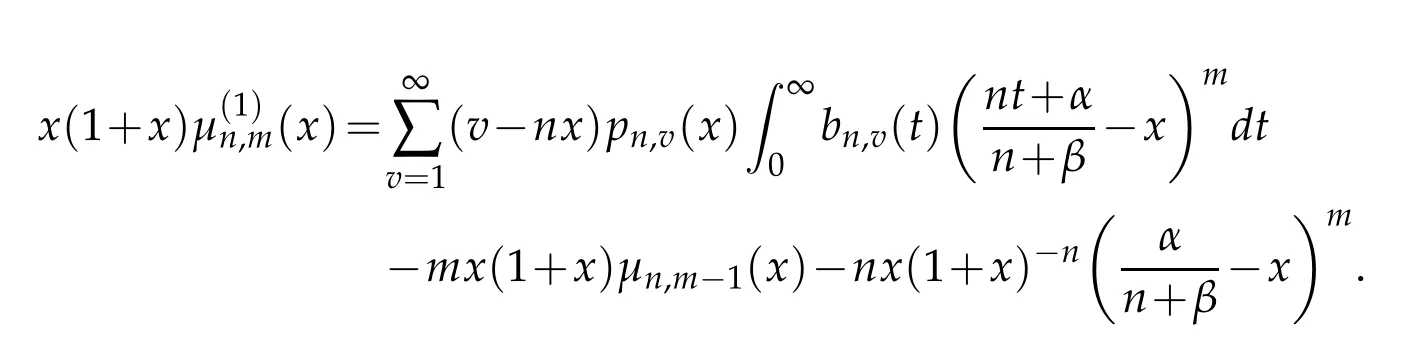
Therefore,

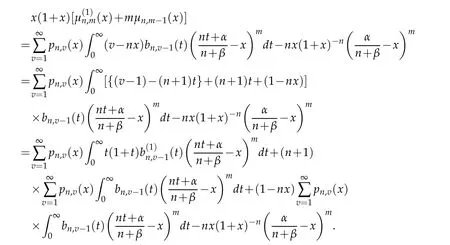
On using the identity

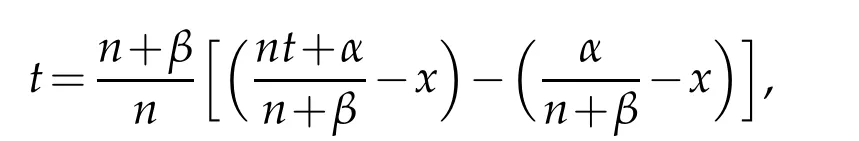
we get

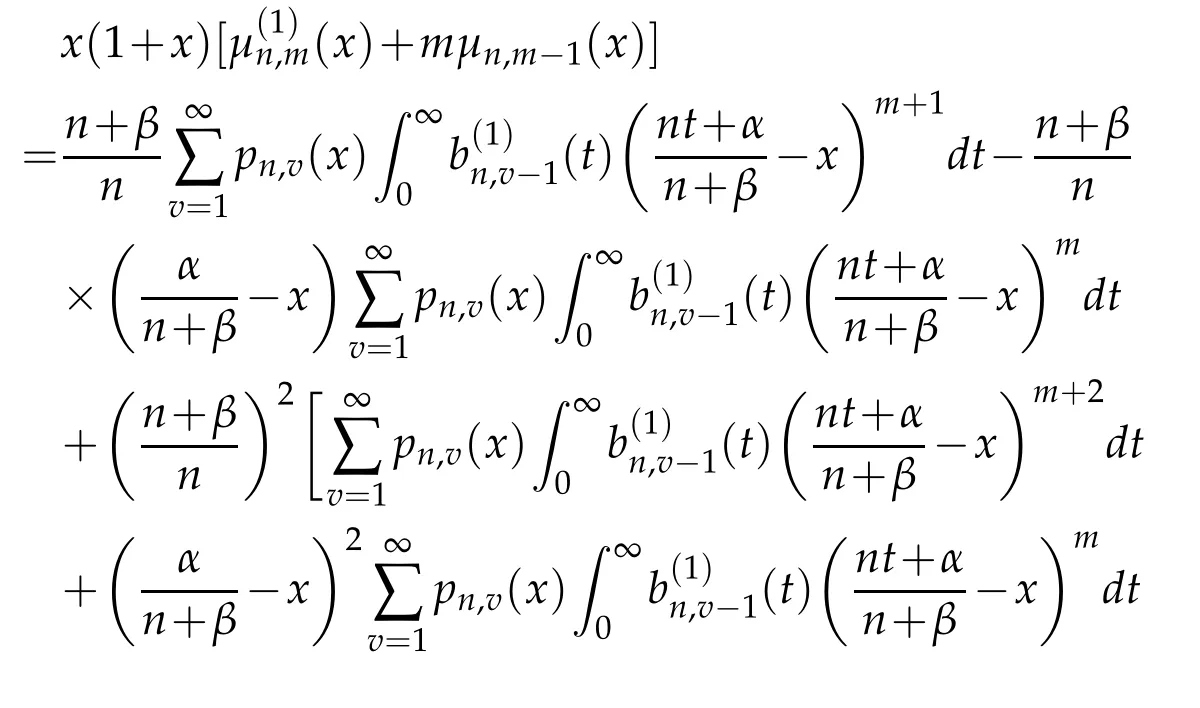
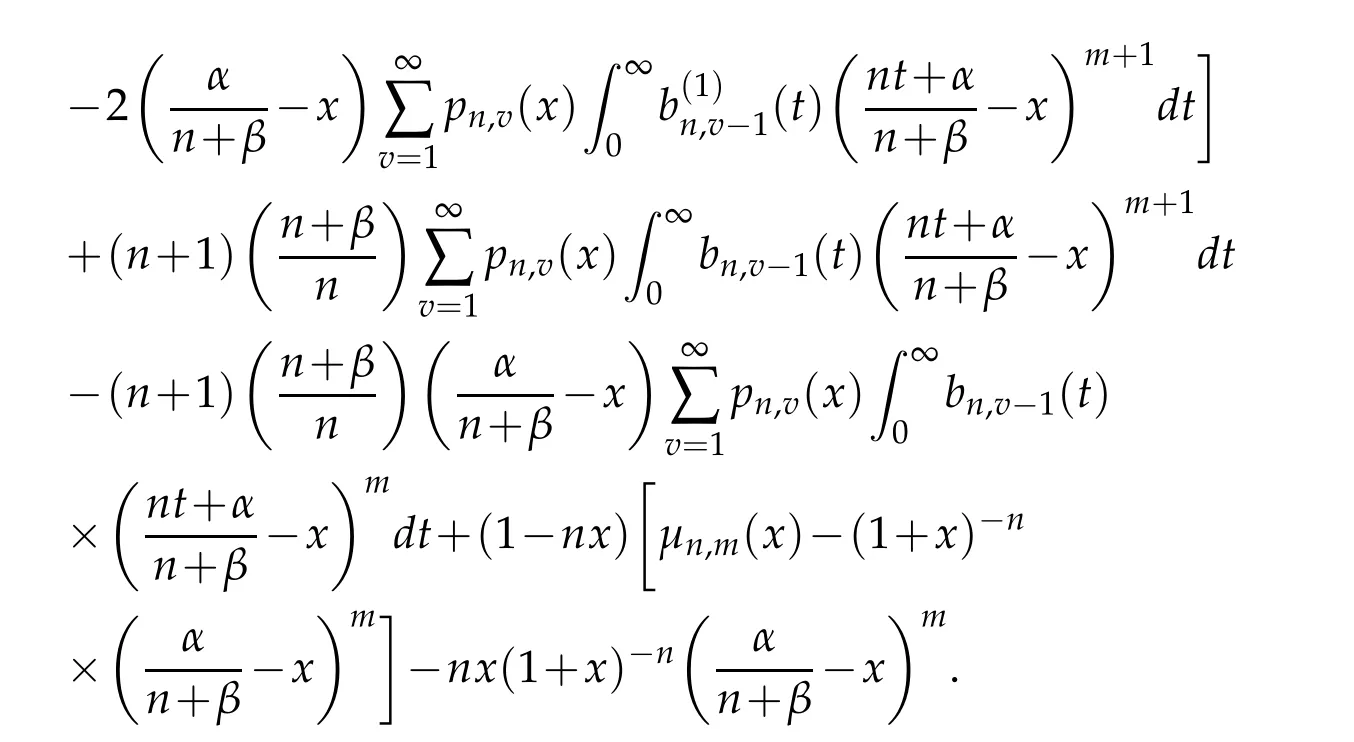
Integrating by parts and rearranging the terms,we get

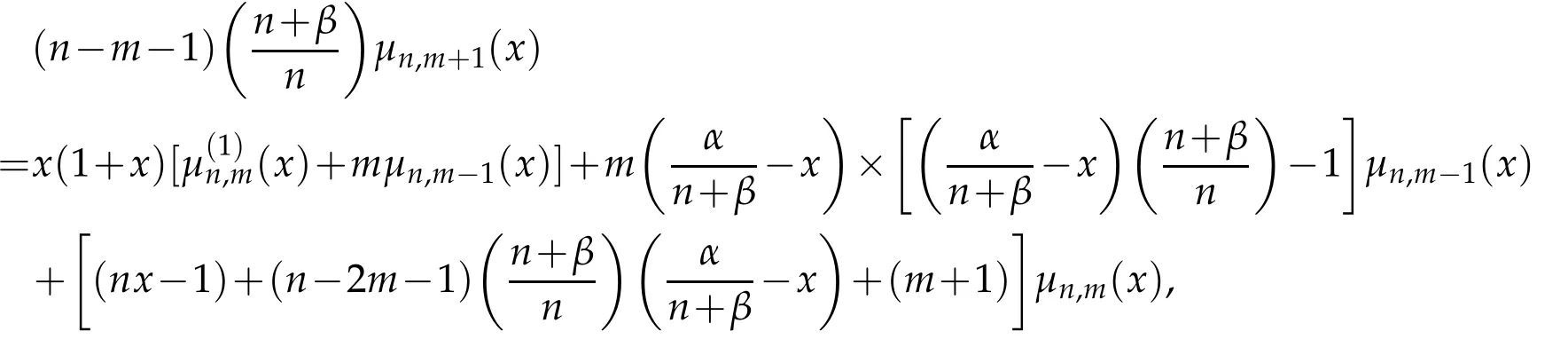
hence the proof is finished.

Lemma 3.5(see[3]).There exists the polynomials φi,j,r(x),independent of n and v such that

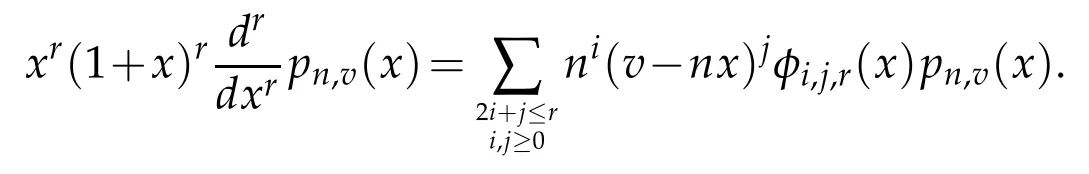
4 Main results

In this section,we prove some direct results including asymptotic formula and error estimation.

Definition 4.1.LetCγ[0,∞)be defined as

then the operatorsare said to be well defined forf∈Cγ[0,∞).

Theorem 4.1.Let f∈Cγ[0,∞)be bounded on every finite subinterval of[0,∞),having the derivatives of order(r+2)at fixed00,then

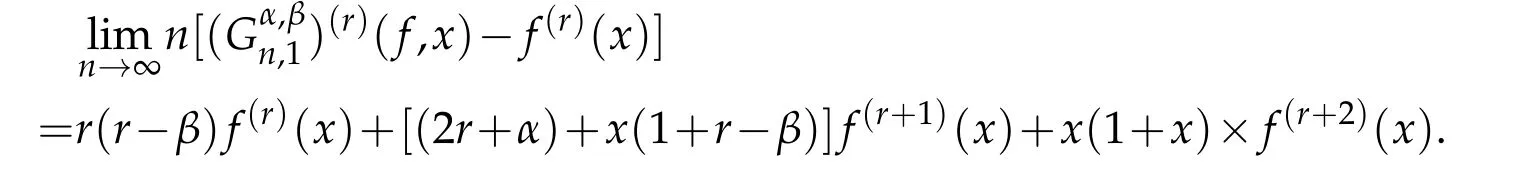
Proof.We have the Taylor’s expansion for the functionfas

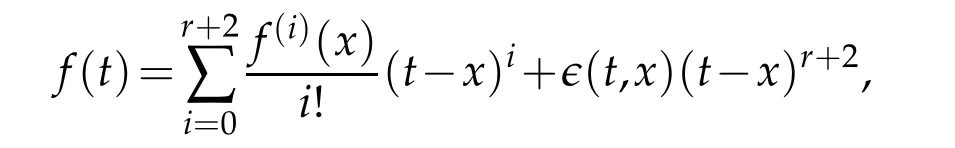
whereǫ(t,x)→0 ast→xandǫ(t,x)=o(t−x)δast→∞,for someδ>0.By using Taylor’s expansion,we have

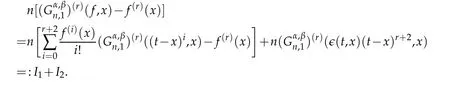
Using Lemma 3.2,we have

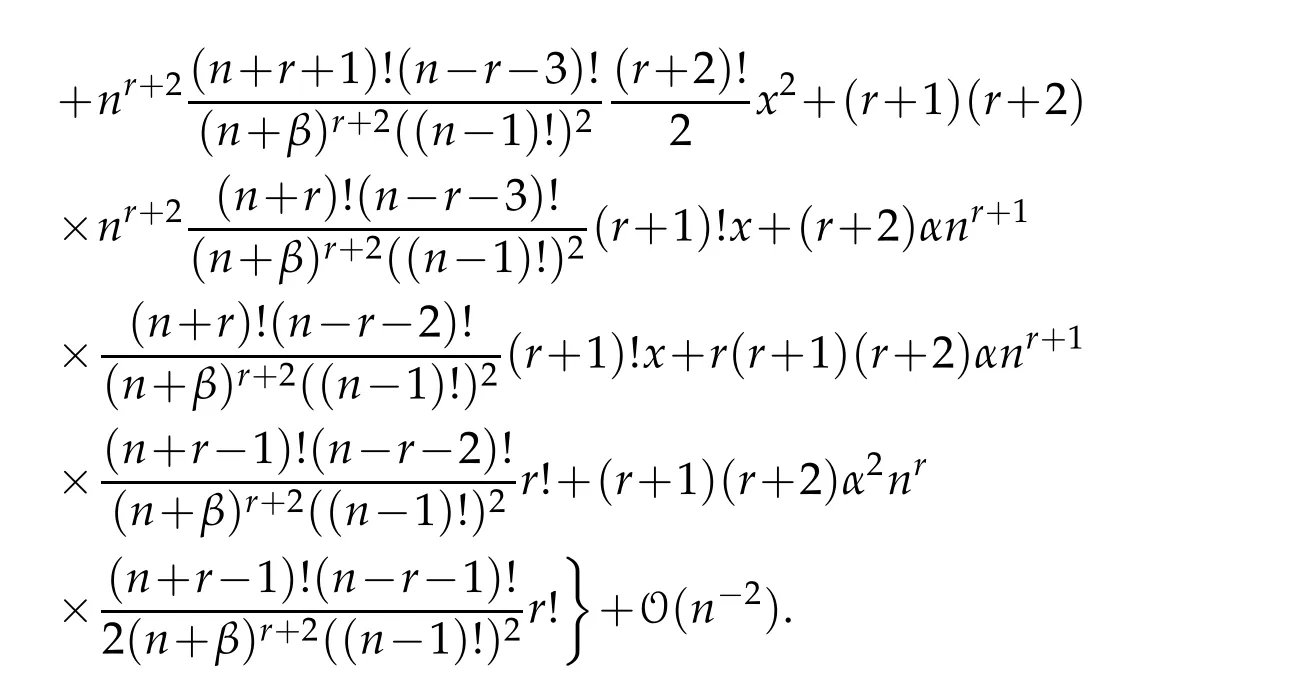
In the above expressionr(r−β),(2r+α)+x(1+r−β)andx(1+x)are the coefficients off(r)(x),f(r+1)(x)andf(r+2)(x)respectively,which easily follow by using induction hypothesis onrand then taking limit asn→∞.Therefore in order to complete the proof of above theorem,it is sufficient to show thatI2→0 asn→∞.For this using Lemma 3.5,we have

asǫ(t,x)→0 whent→x,hence for a givenǫ>0,there exists a positive numberδ:|ǫ(t,x)|<ǫwhenever|t−x|<δ.Ifλis any integer≥max{λ,r+2}then for a constantM>0,which does not depend ont,we have

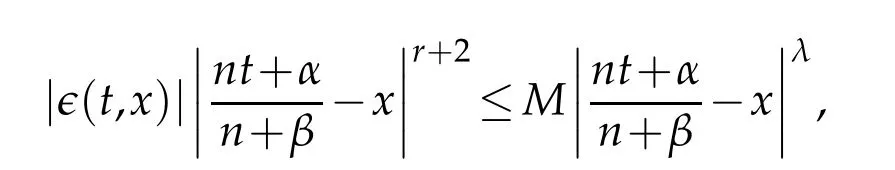
where|t−x|≥δ.Hence

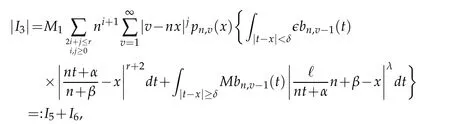
where

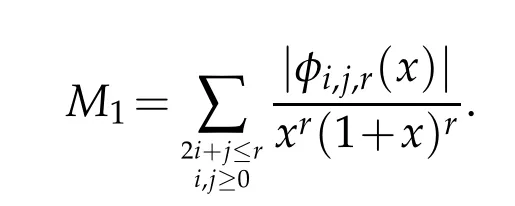
Using Schwarz’s inequality,we have

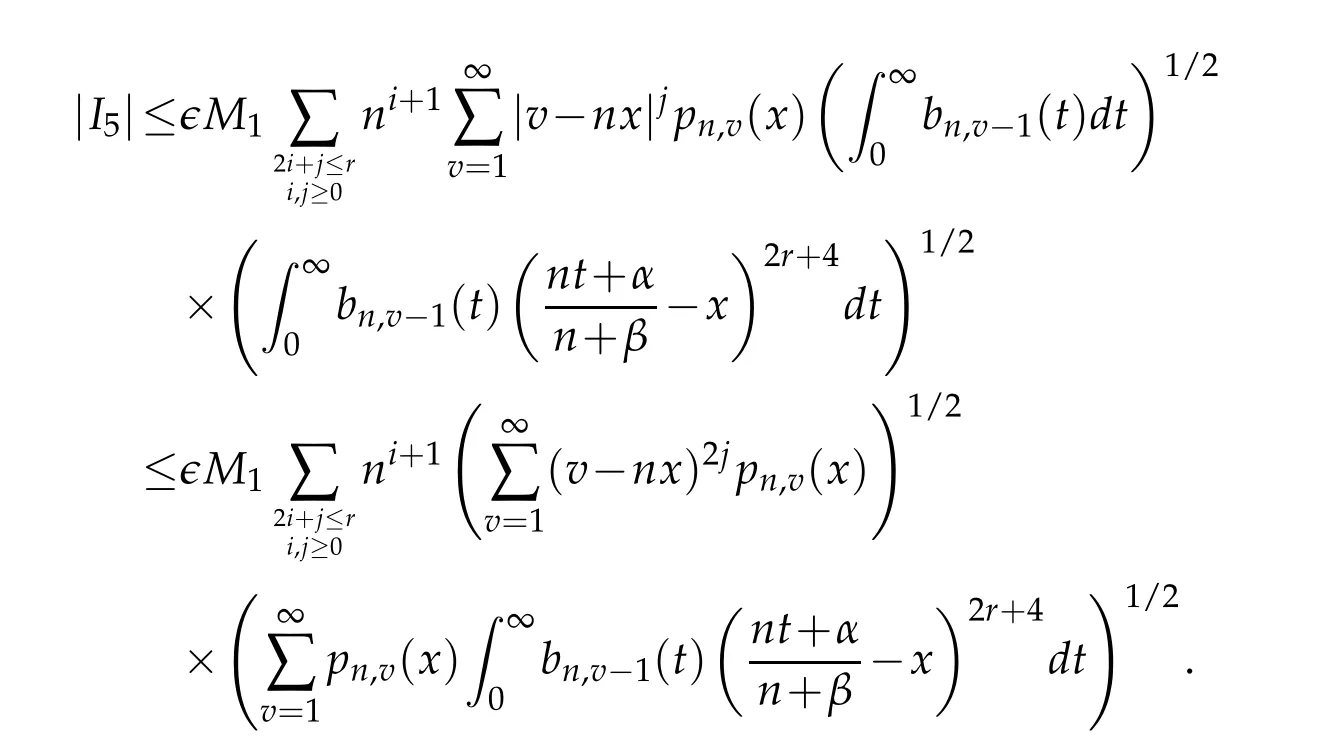
On using Lemma 3.3 and Lemma 3.4,we have

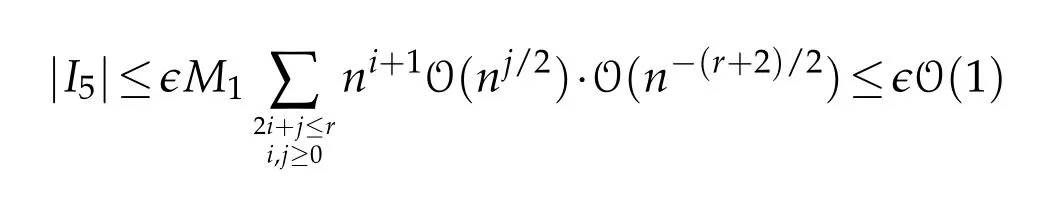
and asǫis arbitrary,it implies thatI5=o(1).

Again applying Schwarz’s inequality for summation and integration and then applying Lemma 3.3 and Lemma 3.4,we have

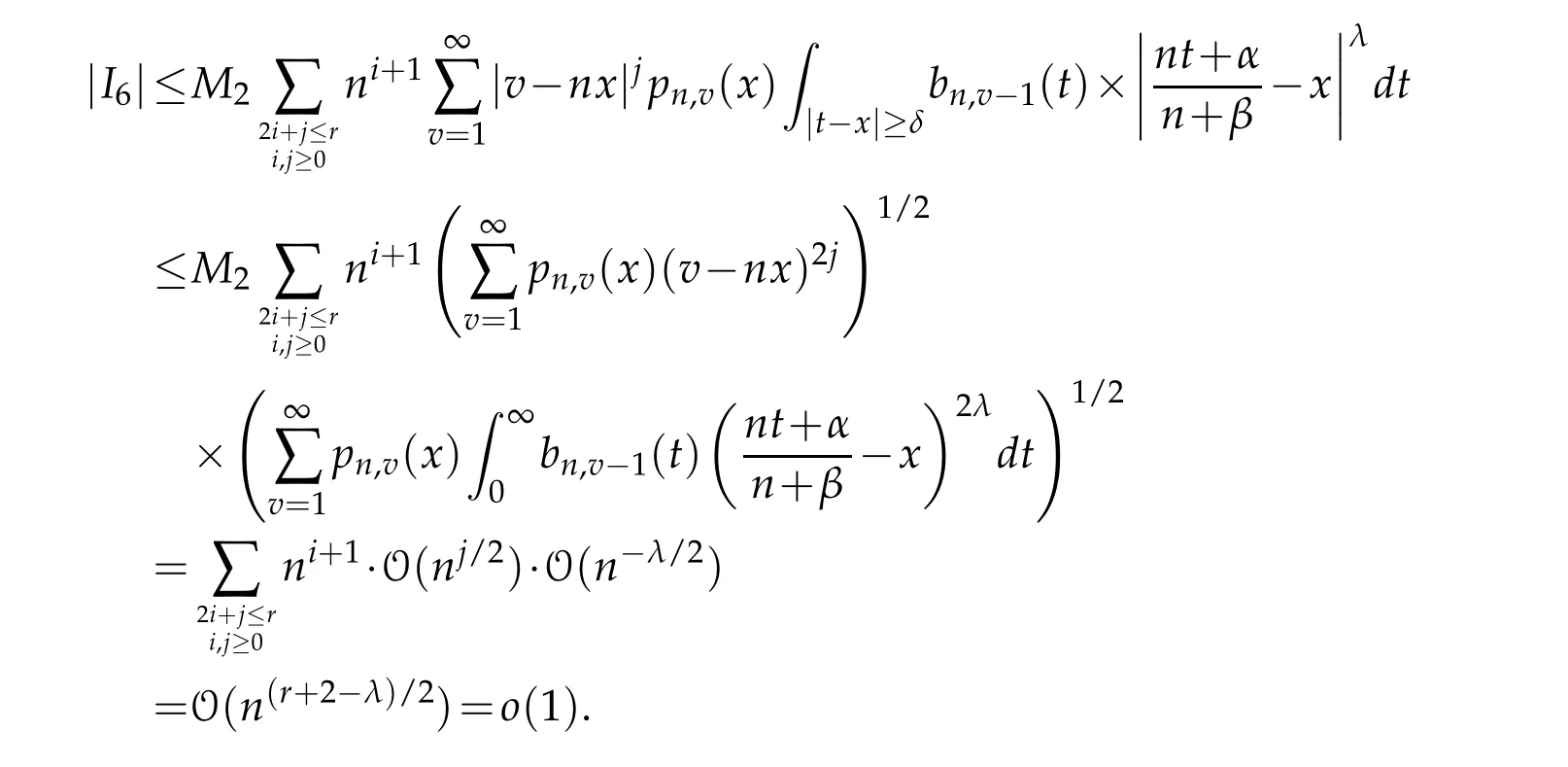
HenceI3→0 asn→∞.Since it is clear thatI4→0 asn→∞,we getI2=o(1).Combining the estimates ofI1andI2,we get the required result.

Hence the proof of the theorem is completed.

Theorem 4.2.For f∈Cγ[0,∞),for some γ>0and r≤k≤r+2.If f(k)exists and is continuous on(a−η,b+η)⊂(0,∞),where η>0,then for sufficiently large n

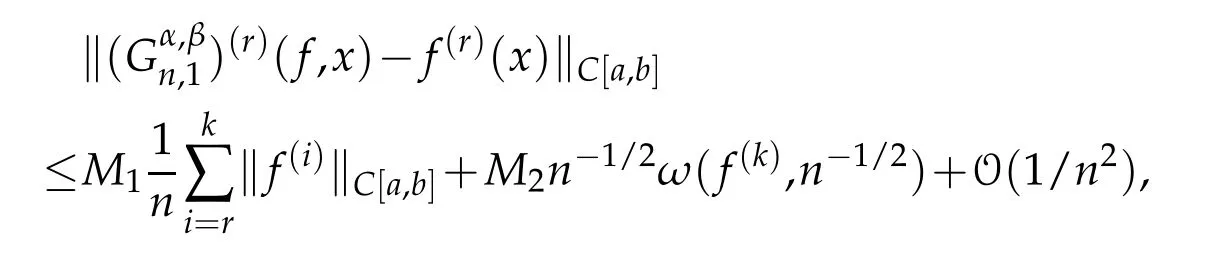
where M1and M2are constants independent of f and n,ω(f,δ)is the modulus of continuity of f on(a−η,b+η)andk·kC[a,b]denotes the sup-norm on the interval[a,b].

Proof.Using Taylor’s expansion on functionf,we have

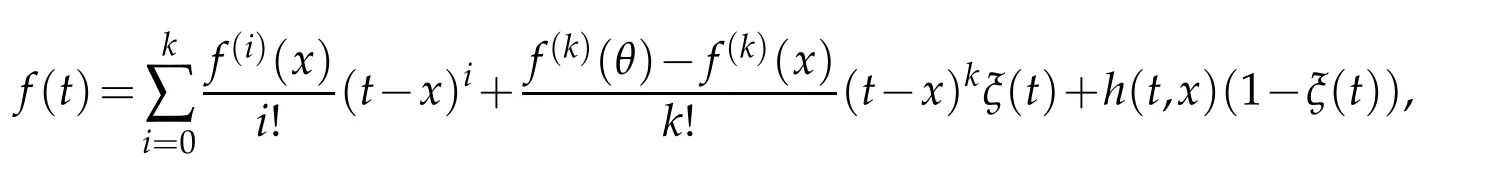
whereθlies betweentandx,andξ(t)is the characteristic function on the interval(a−η,b+η).Therefore

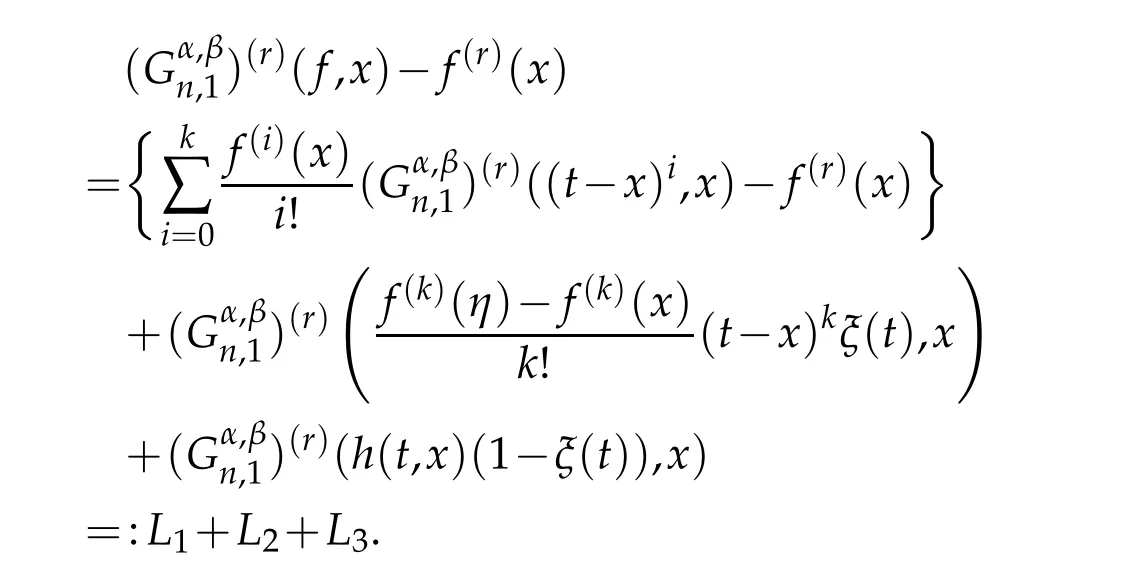
Using Lemma 3.2,we have

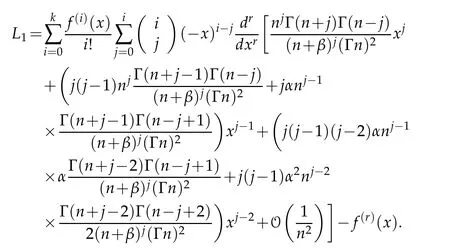
Hence

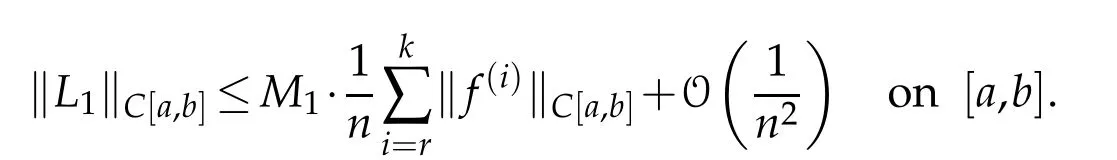
To estimateL2,we follow

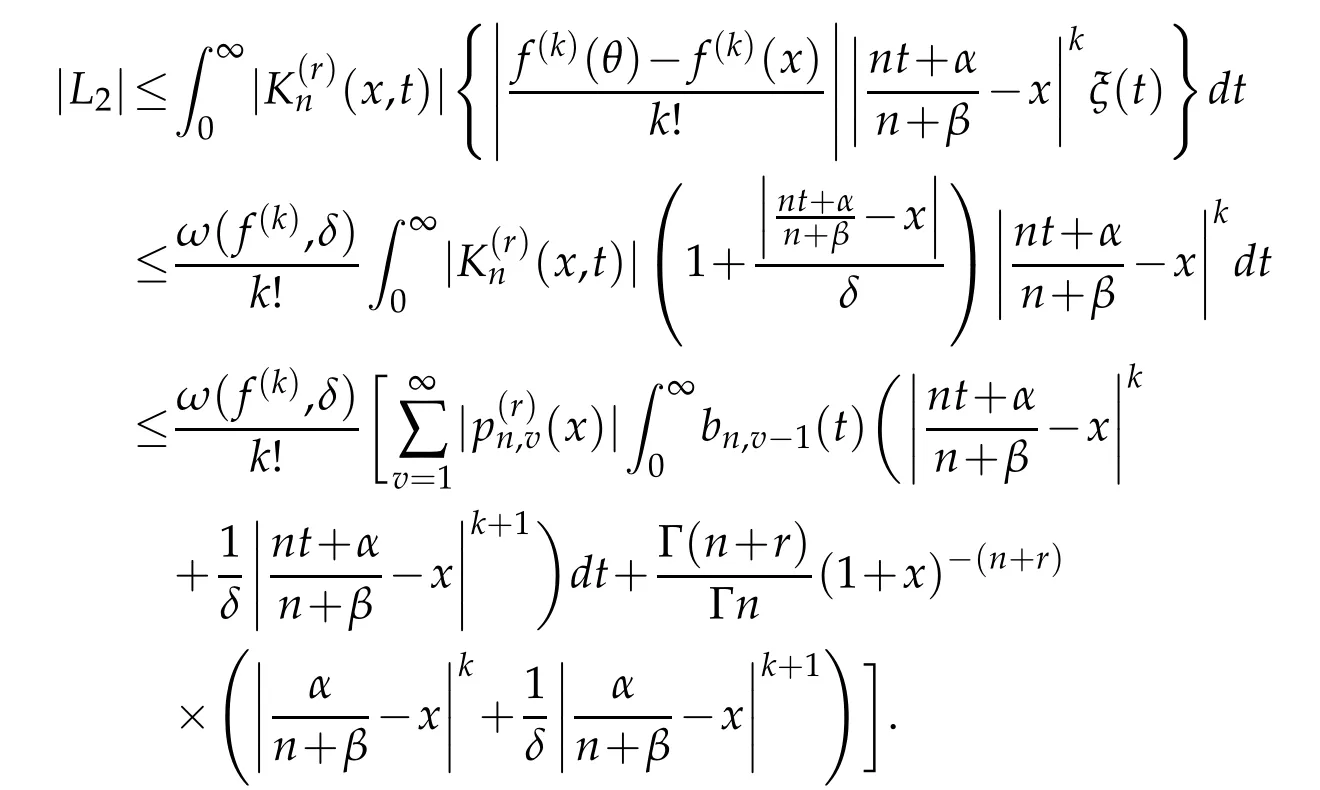
By applying Schwarz’s inequality for summation and integral,we have

Therefore by Lemma 3.5 and(4.1),we get

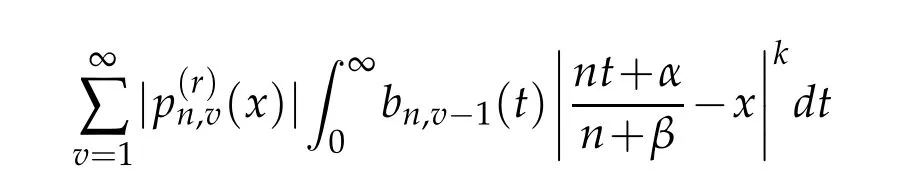
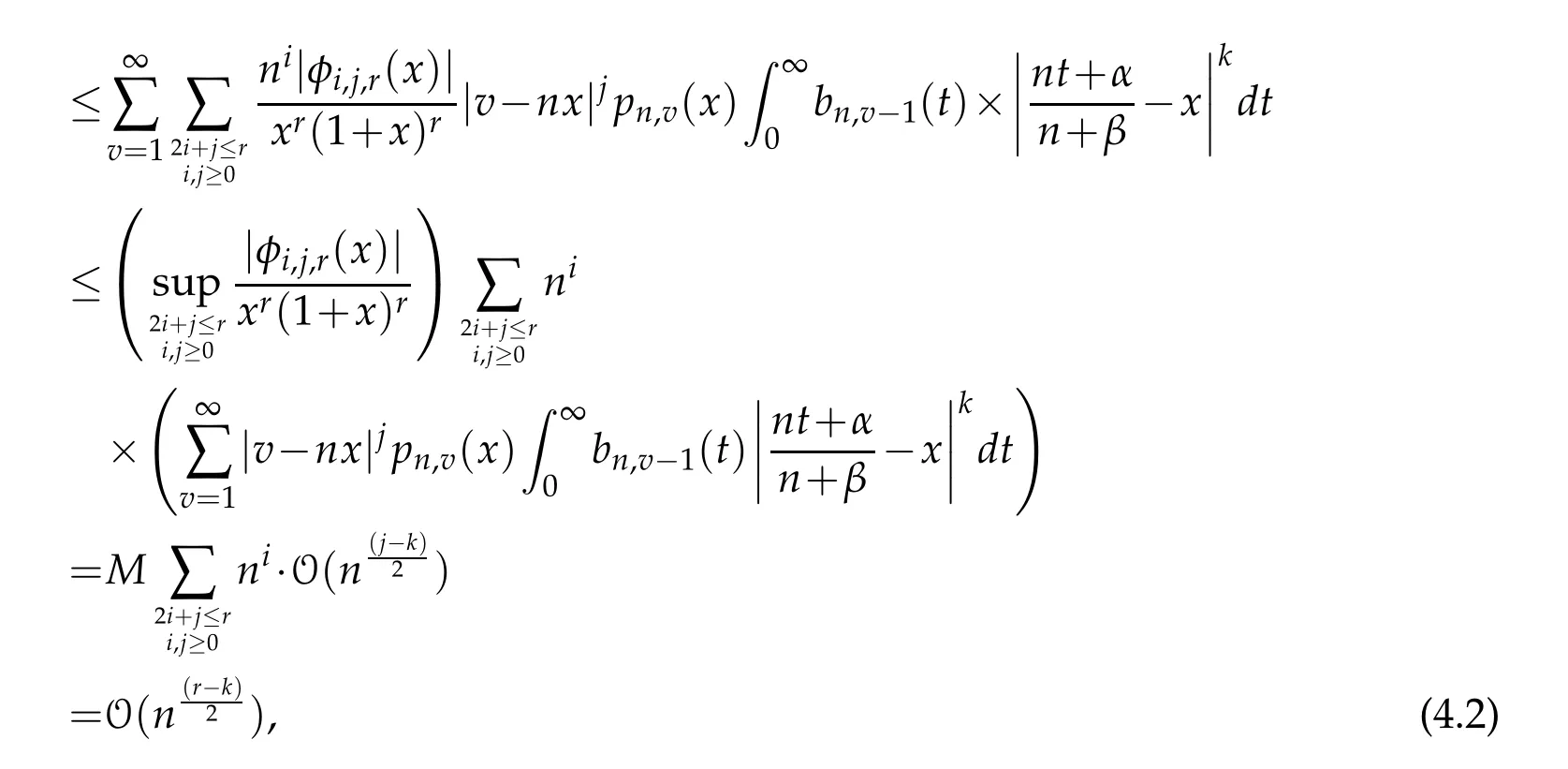
on[a,b],where

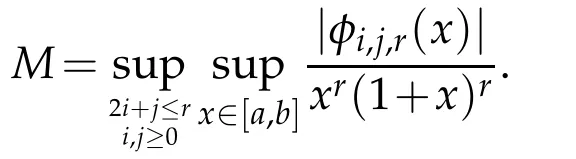
If we chooseδ=1/√and apply(4.2)we have

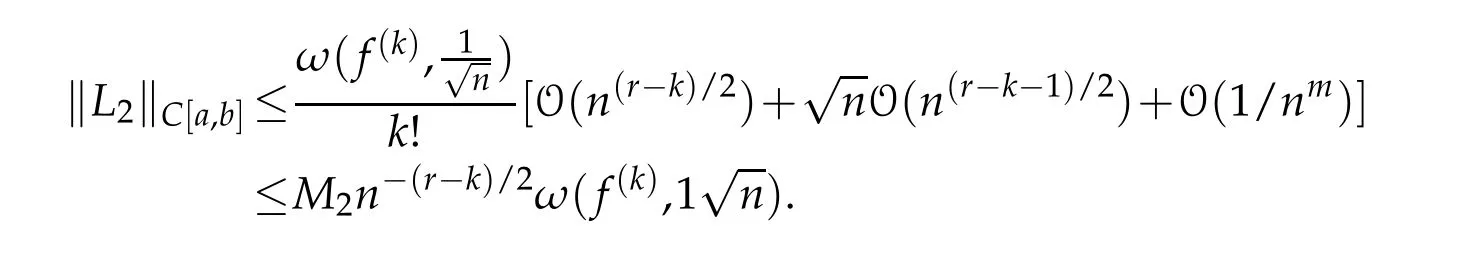
Sincet∈[0,∞)(a−η,b+η),here we optδsuch that|t−x|≥δfor allx∈[a,b].Hence by Lemma 3.5

for|t−x|≥δ,we find a constantKsuch that

whereβ≥ {γ,k}is an integer.Therefore by using Schwarz’s inequality for summation and integration and using Lemma 3.3 as well as Lemma 3.4,we follow thatL3=O(1/ns),for anys>0 uniformly on[a,b].

Combining the estimates ofL1,L2andL3,we get the required result.

Acknowledgements

The author would like to thank to the referees for their valuable suggestion in improving the quality of paper.Author is also thankful to National Board of Higher Mathematics,for providing a plate-form for research.

References

[1]I.Buyukyazici and C.Atakut,On Stancu type generalization ofq-Baskakov operators,Math.Comput.Model.,52(5-6)(2010),752–759.

[2]N.Deo,Faster rate of convergence on Srivastava-Gupta operators,Appl.Math.Comput.,218(21)(2012),10486–10491.

[3]V.Gupta,Errorestimates for mixed summation integral type operators,J.Math.Anal.Appl.,313(2006),632–641.

[4]V.Gupta,R.N.Mohapatra and Z.Finta,On certain family of mixed summation-integral operators,Math.Comput.Model.,42(2005),181–191.

[5]V.Gupta and P.Maheshwari,Bezier variant of a new Durrmeyer type operators,Rivista Di Mate.Della Univ.di Parma,7(2)(2003),9–21.

[6]M.Ismail and P.Simeonov,On a family of positive linear operators in:notions of positively and the geometry of polynomials,Trends in Mathematics,(2011),259–274.

[7]N.Ispir and I.Yuksel,On the Bezier variant of Srivastava-Gupta operators,Appl.Math.E-Notes,5(2005),129–137.

[8]S.M.Majharand and V.Totik,Approximation by modified Szasz operators,Acta.Sci.Math.,49(1985),257–269.

[9]P.Maheshwari,Approximation properties of certainq-genuine Szasz operators,Complex Analysis and Operator Theory,DOI 10.1007/s11785-016-0538-3(2016),1–10.

[10]P.Maheshwari,On modified Srivastava-Gupta operators,Filomat,29(6)(2015),1173–1177.

[11]P.Maheshwari,Saturation theorem for the combinations of modified Beta operators inLpspaces,Appl.Math.E-Notes,7(2007),32–37.

[12]P.Maheshwari,An Inverse result in simultaneous approximation of modified Beta operators,Georgian Math.J.,13(2)(2006),297–306.

[13]P.Maheshwari and D.Sharma,Approximation byq-Baskakov-Beta-Stancu operators,Rend.Circ.Mat.Palermo,61(2012),297–305.

[14]R.S.Phillips,An inversion formula for semi-groups of linear operators,Ann.Math.,59(2)(1954),352–356.

[15]H.M.Srivastavaand V.Gupta,A certain family of summation integral type operators,Math.Comput.Model.,37(12-13)(2003),1307–1315.

[16]D.K.Verma and P.N.Agarwal,Convergence in simultaneous approximation for Srivastava-Gupta operators,Math.Sci.,6(22)(2012),doi:10.1186/2251-7456-6-22.

[17]D.V.Widder,The Laplace Transform,Princeton University Press,Princeton 1941.