Some Generalized q-Bessel Type Wavelets and Associated Transforms
2018-05-24ImenRezguiandAnouarBenMabrouk
Imen Rezguiand Anouar Ben Mabrouk,2,3,∗
1Algerba,Number Theory and Nonlinear Analysis Research Unit,UR11ES50,Department of Mathematics,Faculty of Sciences,Monastir 5000,Tunisia
2Department of Mathematics,Higher Institute of Applied Mathematics and Informatics,Street of Assad Ibn Alfourat,Kairouan University,3100 Kairouan Tunisia
3Department of Mathematics,Faculty of Sciences,University of Tabuk,KSA
1 Introduction and brief review
Wavelet theory has been known a great success since the eighteenth of the last century.It provides for function spaces as well as time series good bases allowing the decomposition of the studied object into spices associated to different horizons known as the levels of decomposition.A wavelet basis is a family of functions obtained from one function known as the mother wavelet,by translations and dilations.Due to the power of their theory,wavelets have many applications in different domains such as mathematics,physics,electrical engineering,seismic geology.This tool permits the representation ofL2-functions in a basis well localized in time and in frequency.Hence,wavelets are special functions characterized by special properties that may not be satisfied by other functions.In the present context,our aim is to develop new wavelet functions based on some special functions such as Bessel one.Bessel functions form an important class of special functions and are applied almost everywhere in mathematical physics.They are also known as cylindrical functions,or cylindrical harmonics,because of their strong link to the solutions of the Laplace equation in cylindrical coordinates.We aim precisely to apply the generalizedq-Bessel function introduced in the context ofq-theory and which makes a general variant of Bessel,Bessel modified andq-Bessel functions.
To organize this paper,we will briefly review in the rest of this section the wavelet theory on the real line.In Section 2,the basic concepts on Bessel wavelets are presented.Section 3 is devoted to the presentation of the extension to theq-Bessel wavelets.Section 4 is concerned with the developments of our new extension to the case of generalizedq-Bessel wavelets.Backgrounds on wavelets,q-theory,q-wavelets and related topics may be found in[2,5,6,8,10,11,26]and the references therein.
We now recall some basic definitions and properties of wavelets on R.For more details we may refer to[18,24].InL2(R),a wavelet is a functionψ∈L2(R)satisfying the so-called admissibility condition
From translations and dilations ofψ,we obtain a family of wavelets{ψa,b}
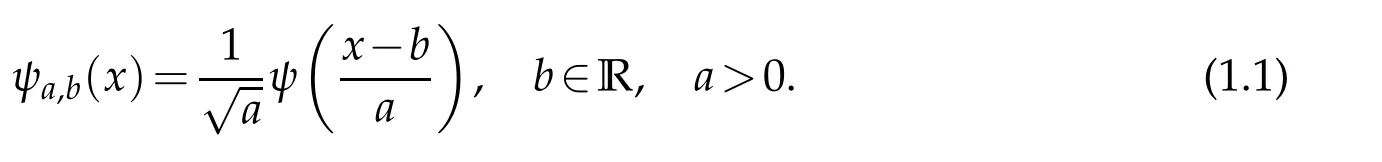
ψis called the mother wavelet.a is the parameter of dilation(or scale)and b is the parameter of translation(or position).
The continuous wavelet transform of a functionf∈L2(R)at the scaleaand the positionbis given by
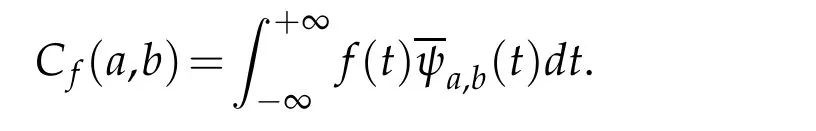
The wavelet transformCf(a,b)has several properties.
•It is linear,in the sense that
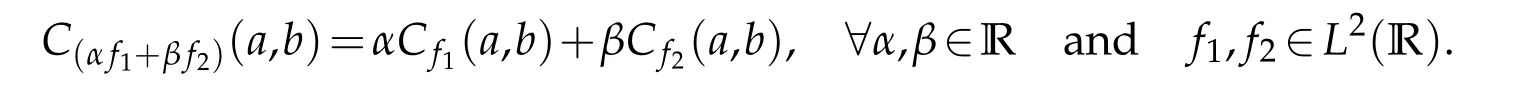
•It is translation invariant:
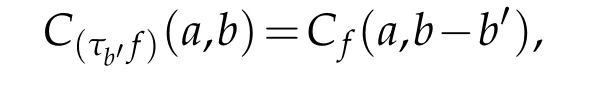
whereτb′refers to the translation offbyb′given by
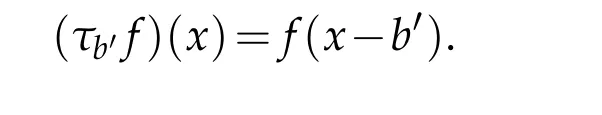
•It is dilation-invariant,in the sense that,iffsatisfies the invariance dilation propertyf(x)=λf(rx)for someλ,r>0 fixed,then
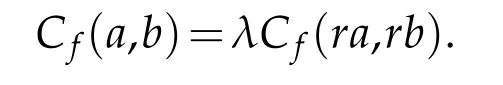
As in Fourier or Hilbert analysis,wavelet analysis provides a Plancherel type relation which permits itself the reconstruction of the analysed function from its wavelet transform.More precisely we have
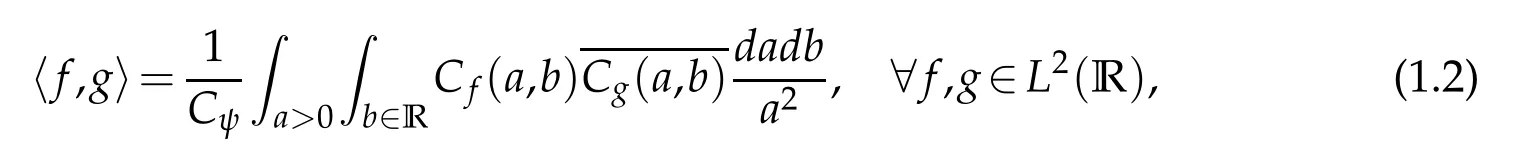
which in turns permit to reconstruct the analyzed functionfin theL2sense from its wavelet transformCa,b(f)as
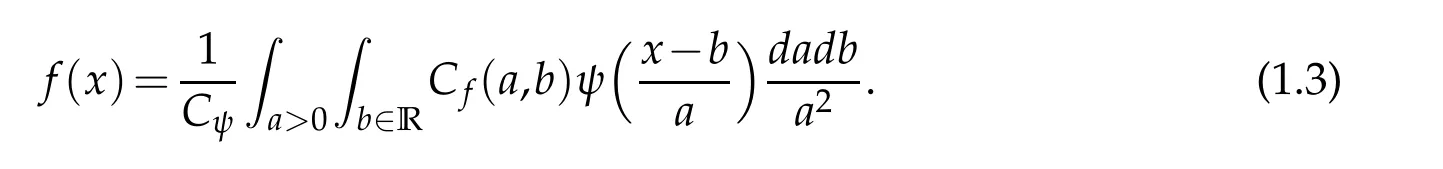
2 Bessel wavelets
There are in literature several approaches to introduce Bessel wavelets.We refer for instance to[22,23].As its name indicates,Bessel wavelets are related to special functions namely the Bessel one.Historically,special functions differ from elementary ones such as powers,roots,trigonometric,and their inverses mainly with the limitations that these latter classes have known.Many fundamental problems such that orbital motion,simultaneous oscillatory chains,spherical bodies gravitational potential were not best described using elementary functions.This makes it necessary to extend elementary functions’classes to more general ones that may describe well unresolved problems.The present section aims to present basics about Bessel wavelets.For 1≤p<∞andµ>0,denote
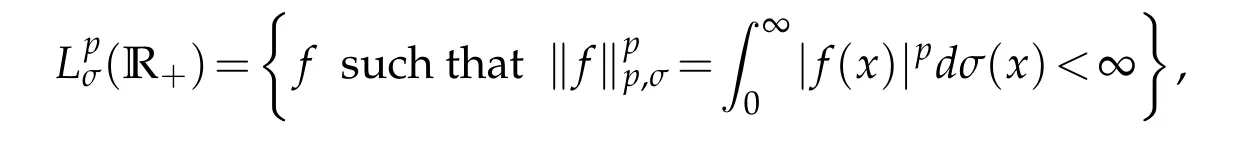
wheredσ(x)is the measure defined by
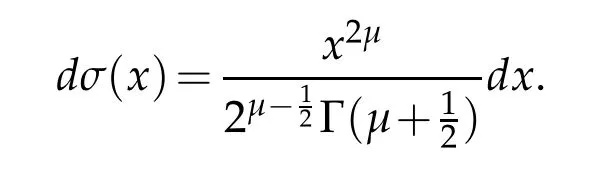
Denote also
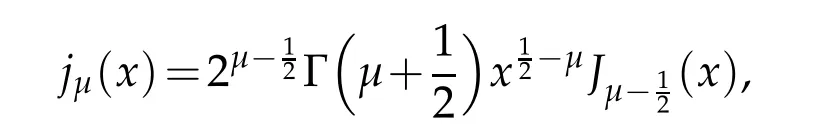
where(x)is the Bessel function of orderv=given by
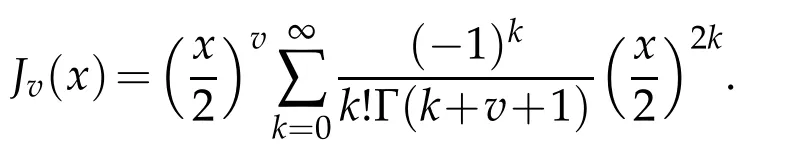
Denote next
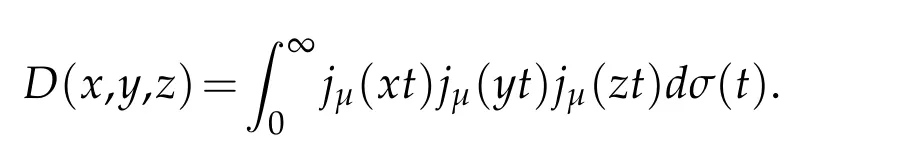
For a 1-variable functionf,we define a translation operator
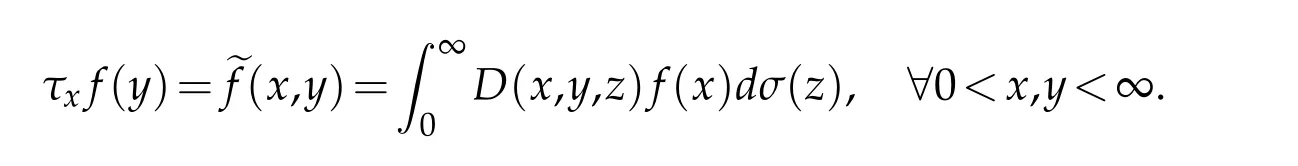
and for a 2-variables functionf,we define a dilation operator
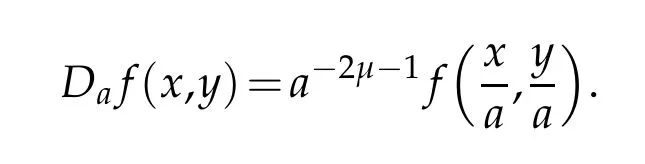
Recall that
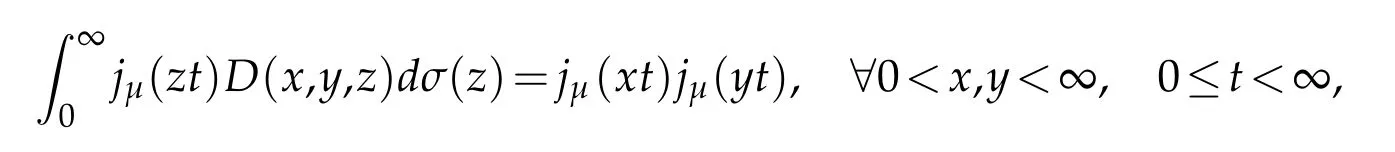
and
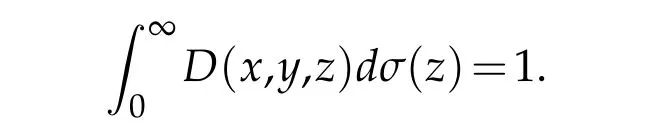
(see[22]).The Bessel Wavelet copies Ψa,bare defined from the Bessel wavelet mother Ψ ∈L2σ(R+)by
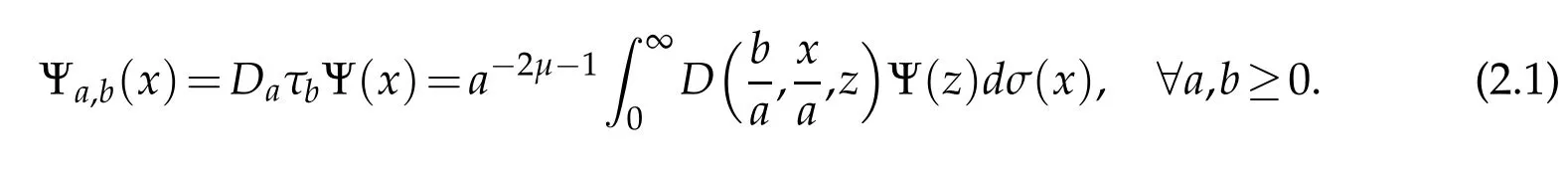
As in the classical wavelet theory on R,we define here also the continuous Bessel Wavelet transform(CBWT)of a functionf∈R+),at the scaleaand the positionbby
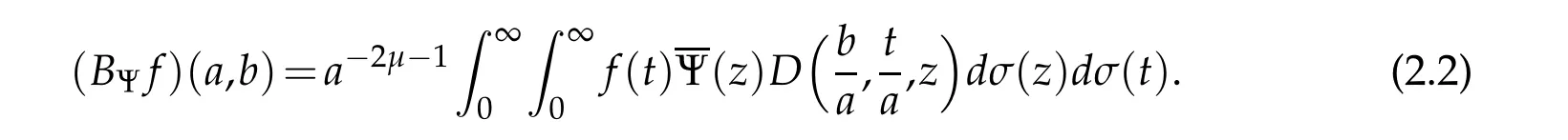
It is well known from Bessel wavelet theory that such a transform is a continuous function according to the variable(a,b).The following result is a variant of Parceval/Plancherel rules for the case of Bessel wavelet transform.
Theorem 2.1(see[22]).
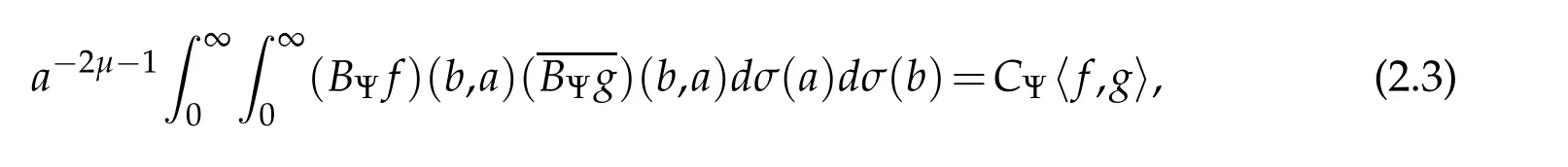
whenever
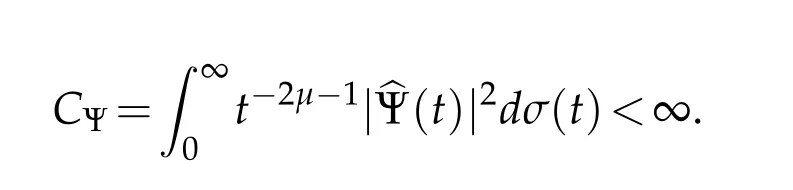
Indeed,
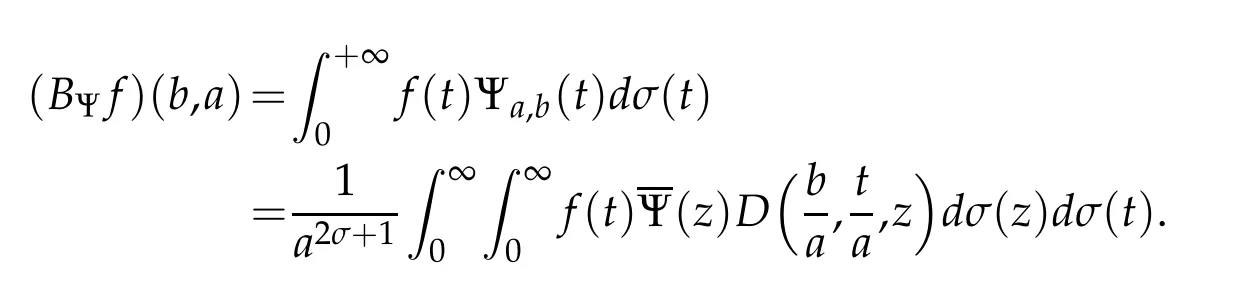
Now,observe that
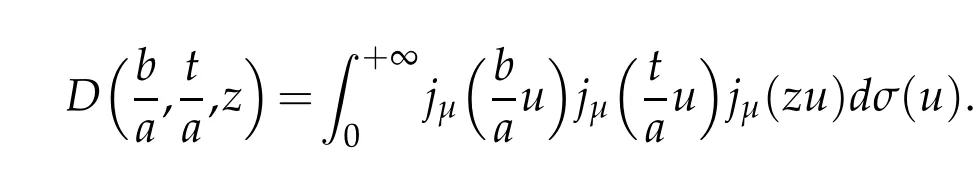
Hence,
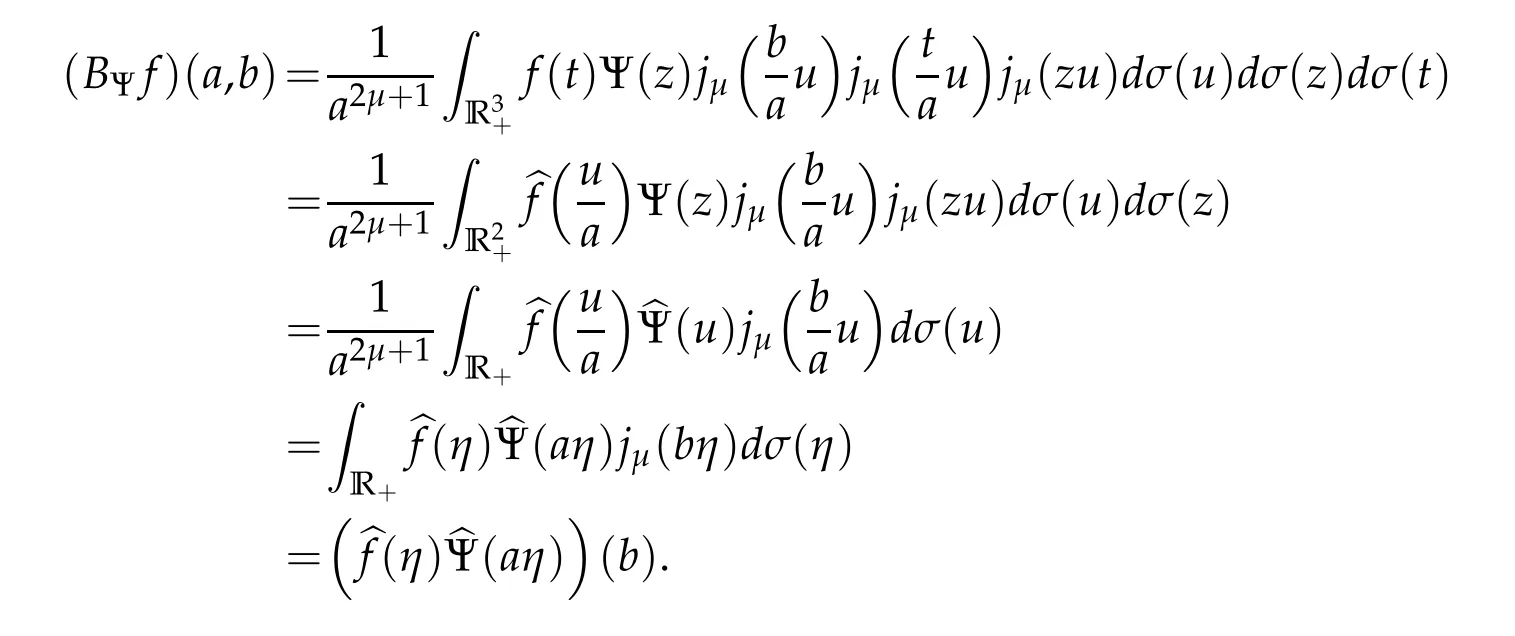
As a result,
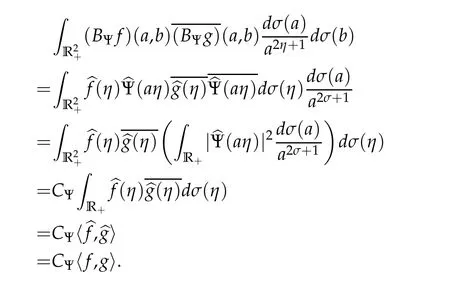
3 q-Bessel wavelets
At the beginning of the twentieth century Jackson introduced the theory ofq-analysis by defining the notions ofq-derivative andq-integral and givingq-analogues of certain special functions such as Bessel’s one.By virtue of their utilities,special functions andq-special functions continue to be a fascinating research topic.Many of these special functions are related to mathematical physics and play an important role in mathematical analysis.This is particularly the case forq-Bessel functions,which represent one of the most important examples ofq-special functions.In the present section we propose to review the basic developments ofq-Bessel wavelets which is the starting point to be able to develop next our extension for the generalizedq-Bessel case.Backgrounds onq-theory andq-wavelets may be found in[5,6,8,10,11,17,26]and the references therein.
For 0 On,theq-Jackson integrals from 0 toaand from 0 to+∞are defined respectively by and provided that the sums converge absolutely.On[a,b]the integral is given by (see[3,11,17]).This allows to introduce next the functional space where whereα>fixed.Denote next,the space of functions defined on,continuous at 0 and vanishing at+∞,equipped with the induced topology of uniform convergence such that Finally,designates the space of functions that are continuous at 0 and bounded on Theq-derivative of a functionf∈Lq,p,α()is defined by Theq-derivative of a function is a linear operator.However,for the product of functions we have a different form, and wheneverg(x)6=0 andg(qx)6=0,we have Inq-theory,we posses an analogues of the integration by parts rule(see[1]). where the integration is understood inq-Jackson sense. We now introduce the normalizedq-Bessel function(see[5]) where theq-shifted factorial are defined by We recall also theq-Bessel operator defined for allfby Theq-Bessel operator is related to the normalizedq-Bessel function by the eigenvalue equation More precisely,jα(x,q2)is the unique solution of the Laplace eigenvalue problem forλ∈C, The following relations are easy to show.The first is an analogue of Stokes rule and states that forf,g∈Lq,2,α()such that∆q,αf,∆q,αg∈Lq,2,α(),we have Recall that in general,the equality(3.3)above is not true(see Proposition 1 in[7]for more details and for more general situations).Next,as a result,we get an orthogonality relation for the normalizedq-Bessel function(see[8])as where and We now recall theq-Bessel Fourier transform Fq,αalready defined in([5])as wherecq,αis given by(3.4)and theq-Bessel translation operator defined next by wherecq,αis already the same constant given by(3.4),Such a translation operator satisfies for allf∈Lq,2,α()a Fourier invariance property(see[8]) It satisfies also forf∈Lq,2,α(), and Definition 3.1(see[11]).Aq-Bessel wavelet is an even function Ψ∈Lq,2,α()satisfying the following admissibility condition, The continuousq-Bessel wavelet transform of a functionf∈Lq,2,α()is defined by where and Several authors have studied the behavior of the wavelet transform as a function of the scale and position variables(a,b)for continuity for example(see[13,20–22,25]).Even in classical wavelet theory,the wavelet transform is considered as a product convolution transform with respect to the scaleaand a convolution transform with respect to the positionb.However,it is well known from functional spaces theory that as the analyzing waveletψis inL2(Rn)and also the analyzed functionf,then the convolutionf∗ψwill lie also inL2(Rn).BUt it remains questionable if the transformation(a,b)7→Cf(a,b)is continuous or not.In the present case,we have the following result. Proposition 3.1.Let Ψ be aq-Bessel wavelet in 1.The functionis continuous on 2.For althe functionis continuous on Proof.1.It is clear thatFis a mapping fromintoSo,we have However,for allwe have andSo,the Lebesgue theorem leads to Assertion 2.follows immediately from 1.as whereKq,αis a positive constant depending onqandα. The following result is a variant of Parceval-Plancherel Theorem for the case ofq-Bessel wavelet transform. Theorem 3.1(see[11]).LetΨbe a q-Bessel wavelet in The proof is easy and may be gathered from[3]and[11]. In this part,the purpose is to generalize the previous results onq-Bessel wavelets to the case of generalizedq-Bessel wavelets by replacing theq-Bessel function with a more general one.This latter have been introduced in[9].The reader may refer to this reference for backgrounds on such function and its properties.In the present work,we will not review all such properties.We will recall in a brief way just what we need here.Instead,we propose to introduce new wavelet functions and new wavelet transforms and we will prove some associated famous relations such as Plancherel/Parcevall ones as well as reconstruction formula.Forα,β∈R,we put and for 1≤p<∞,we put Throughout this part we will fix 0 Definition 4.1.The generalizedq-Bessel Fourier transformis defined by where We are now able to introduce the context of wavelets associated to the new generalizedq-Bessel function. Definition 4.2.A generalizedq-Bessel wavelet is an even function Ψ∈Lq,2,v()satisfying the following admissibility condition: To introduce the continuous generalizedq-Bessel wavelet transform of a functionf∈Lq,2,v()at the scalea∈R+qand the positionb∈we need to introduce firstly a translation parameter and a dilation one on the wavelet function Ψ. A generalizedq-Bessel translation operator associated via the generalizedq-Bessel function has been already defined in[9]by It is easy to show that Definition 4.3.The continuous generalizedq-Bessel wavelet transform of a functionf∈Lq,2,v()at the scalea∈and the positionb∈is defined by where Remark 4.1. The following result shows some properties of the generalizedq-Bessel continuous wavelet transform. Theorem 4.1.LetΨbe a generalized q-Bessel wavelet inLq,2,v().Then for all f∈Lq,2,vand all a∈the function(f)(a,·)is continuous onand Furthermore,we have The proof is based on the following preliminary Lemmas. Lemma 4.1.Define the(q,v)-delta operator by The following assertions hold 1.For all f∈Lq,2,v()and all t∈,we have 2.For x,y∈,we have The proof of this Lemma is given in[9,Proposition 8].For the sake of completeness of the present work we reproduce it here. Proofof Lemma 4.1.(1)From the definition of theq-Jackson integral we have wherekis the unique integer such thatt=qk. (2)Letx,y∈.We have whereu=qnt.So We complete the proof. Lemma 4.2. This Lemma is proved in[5]using a different method based on the ability to construct an orthogonal basis of the Hilbert spaceLq,2,ν.Here,we will use differently the result by adopting Fubini’s rule to the context ofq-Jackson integrals(see Appendix).Indeed,denote for simplicity We have The second and the fourth equalities are simple applications of Fubini’s rule.The third one follows from Assertion 2 in Lemma 4.1.Finally,the fifth equality results from Assertion 1 in Lemma 4.1. Lemma 4.3.For all f∈Lq,2,v(),the following assertions are true. Proof.(1)Denote as in Lemma 4.2 and We have As previously,we use Fubini’s rule adopted to the context ofq-Jackson integrals(see Appendix).So,the second and the fourth equalities are simple applications of Fubini’s rule.The third and the fifth ones are applications of the second and the first assertions in Lemma 4.1 respectively.Next,observing that we get (2)Recall that Which by settingyields that We complete the proof. Proofof Theorem 4.1.Fora∈R+qandb∈ eR+q,we have Observing that we get Now using Proposition 4.1(see Appendix)with we obtain Consequently, Hence, Which by Lemma 4.3 implies that Thus,we complete the proof. The following result shows Plancherel and Parceval formulas for the generalizedq-Bessel wavelet transform. Theorem 4.2.LetΨbe a generalized q-Bessel wavelet inLq,2,v().Then we have Proof.(1)We have Hence,the first assertion is proved. (2)may be deduced from the previous assertion by replacingfbyf+gand observing the linearity of the wavelet transform. Theorem 4.3.LetΨis a generalized q-Bessel wavelet inwe have Proof.Forx∈consider the functiong=δq,v(x,·).It is straightforward that Consequently,the right hand part of the Assertion 2 in Theorem 4.2 becomes On the other hand,with the choice ofgabove it follows from Lemma 4.1 that for allf∈Lq,2,v, Consequently, Thus,we complete the proof. Appendix In this appendix we present some analogues in the context ofq-theory of classical rules known in integration theory such as Cachy-Shwartz,Fubini rules.Forp>0 we denote Proposition 4.1.For allf,g∈L2()we have,fg∈L1(and Indeed, Next,the following definition extends in a usual way the notion of Jackson integral to the two dimensional case. Definition 4.4.A functionf:−→C is said to be integrable in theq-Jackson sense iff the series in(4.6)below is absolutely convergent and we define the integral by Now as for the 1-dimensional case,we denote forp>0 Proposition 4.2.For allf∈L1we have, Proof.From Definition 4.4,we have Similarly,we have We complete the proof. Acknowledgements The authors would like to thank the anonymous referee(s)for the suggestions and remarks that have improved the quality of the paper. References [1]A.Aral,V.Gupta and R.P.Agarwal,Applications ofq-Calculs in Operator Theory,Springer,New York,2013. [2]S.Arfaoui,I.Rezgui and A.Ben Mabrouk,Wavelet Analysis on the Sphere:Spheroidal Wavelets,Walter de Gruyter(March 20,2017),ISBN-10:311048109X,ISBN-13:978-3110481099. [3]S.Bouaziz,Theq-Bessel wavelet packets,Adv.Anal.,1(1)(2016),27–39. [4]F.Bouzeffour and H.Ben Mansour,On the zeros of the bigq-Bessel functions and applications,arXiv:1311.1165v1,2013. [5]L.Dhaouadi,On theq-Bessel Fourier transform,Bull.Math.Anal.Appl.,5(2)(2013),42–60. [6]L.Dhaouadi and M.J.Atia,Jacobi operators,q-dfference equations and orthogonal polynomials,arXiv:1211.0359v1,(2012),22 pages. [7]L.Dhaouadi,W.Binous and A.Fitouhi,Paley-Wiener theorem for theq-Bessel transform and associatedq-sampling formula,Expos.Math.,27(2009),55–72. [8]L.Dhaouadi,A.Fitouhi and J.El Kamel,Inequalities inq-Fourier analysis,J.Inequalities Pure Appl.Math.,7(5)(2006),Article 171,14 pages. [9]L.Dhaouadi and M.Hleili,Generalizedq-Bessel operator,Bull.Math.Anal.Appl.,7(1)(2015),20–37. [10]A.Fitouhi and N.Bettaibi,Wavelet transforms in quantum calculus,J.Nonlinear Math.Phys.,13(3)(2006),492–506. [11]A.Fitouhi,N.Bettaibi and W.Binous,Inversion formulas for theq-Riemann-Liouville andq-Weyl transforms using wavelets,Fractional Calculus Appl.Anal.,10(4)(2007),327–342. [12]A.Fitouhi and A.Safraoui,Paley-Wiener theorem for theq2-Fourier-Rubin transform,Tamsui Oxford J.Mathematical Sci.,26(3)(2010),287–304. [13]N.Fukuda,T.Kinoshita and K.Yoshino,Wavelet transforms on Gelfand-Shilov spaces and concrete examples,J.Inequalities Appl.,119(2017),24 pages. [14]G.Gasper and M.Rahman,Basic Hypergeometric Serie Second edition,Combridge university Press,2004. [15]D.T.Haimo,Integral equations associated with Hankel convolution,Trans.Amer.Math.Soc.,116(1965),330–375. [16]I.I.Hirschman,Variation diminishing Hankel transform,Journal d’Analyse Mathmatique,8(1)(1860),307–336. [17]F.H.Jackson,On aq-definite integrals,Quarterly J.Pure Appl.Math.,41(1910),193–203. [18]O.Le Cadet,Mthodes d’ondelettes pour la Segmentation D’images:Applications`a l’Imagerie Mdicale et au Tatouage D’images,Thse de Doctorat en Mathmatiques Appliques,UniversitJoseph Fourier,Grenoble,2004. [19]M.Martinet,Analyse Multirsolution en Ondelettes du Rayonnement Acoustique des Structures Planes,Thse de Doctorat en Acoustique,INSA de Lyon,2001. [20]R.S.Pathak,Continuity and inversion of the wavelet transform,Integral Transforms and Special Functions,6(1-4)(1998),85–93. [21]R.S.Pathak,The wavelet transform of distributions,Tohoku Math.J.,56(2004),411–421. [22]R.S.Pathak and M.M.Dixit,Continuous and discrete Bessel wavelet transforms,J.Comput.Appl.Math.,160(2003),240–250. [23]R.S.Pathak,S.K.Upadhyay and R.S.Pandey,The Bessel wavelet convolution product,Rend.Sem.Mat.Univ.Politec.Torino,96(3)(2011),267–279. [24]A.Prasad,A.Mahato,V.K.Singh and M.M.Dixit,The continuous fractional Bessel wavelet transformation,Boundary Value Problems,40(2013),1–16. [25]A.Prasad,A.Mahato1 and M.M.Dixit,Continuity of the Bessel wavelet transform on certain Beurling-type function spaces,J.Inequalities Appl.,29(2013),9 pages. [26]R.F.Swarttouw,The Hahn-Extonq-Bessel Functions,PhD Thesis,The Technical University of Delft,(1992). [27]S.K Upadhyaya,On continuous Bessel wavelet transformation associated with the Hankel-Hausdorff operator,Integral Transforms and Special Functions,23(5)(2012),315–323.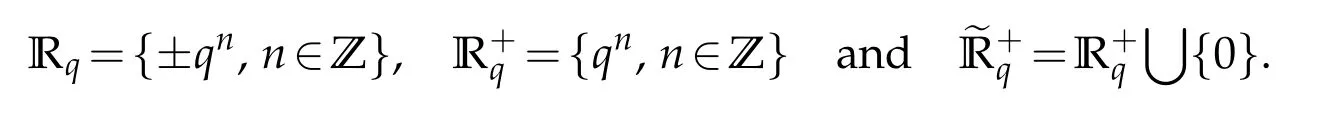
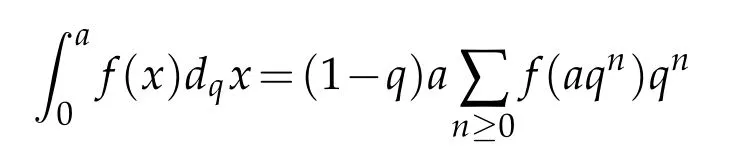
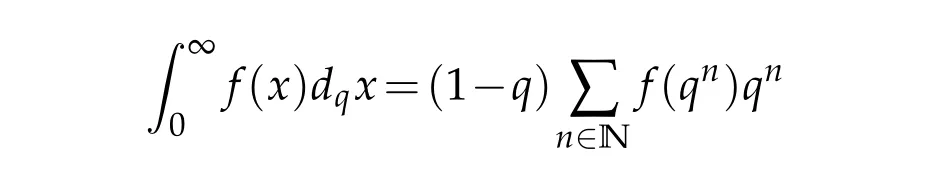
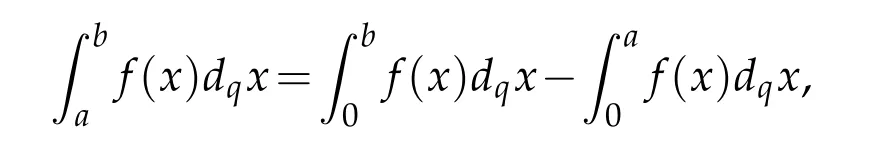
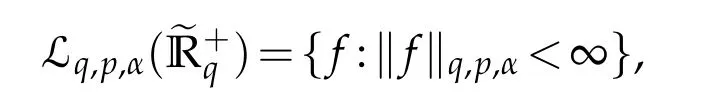
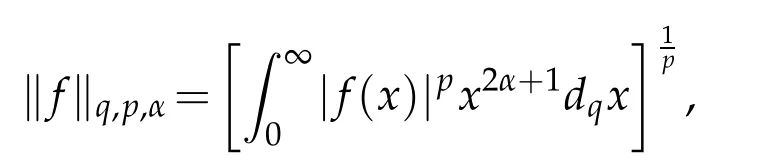
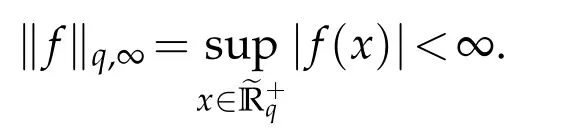
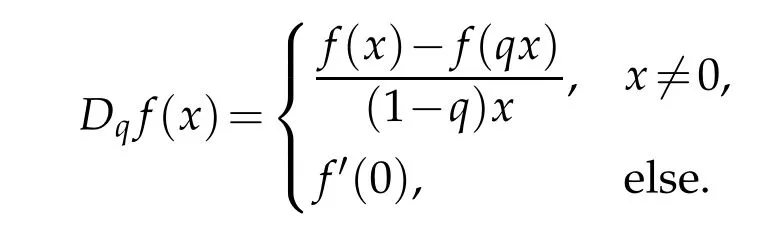
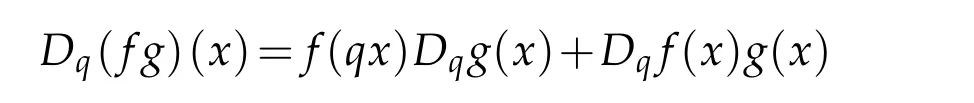
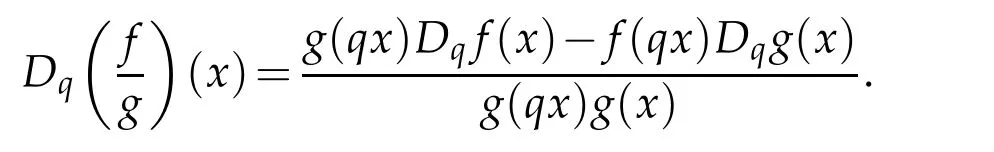
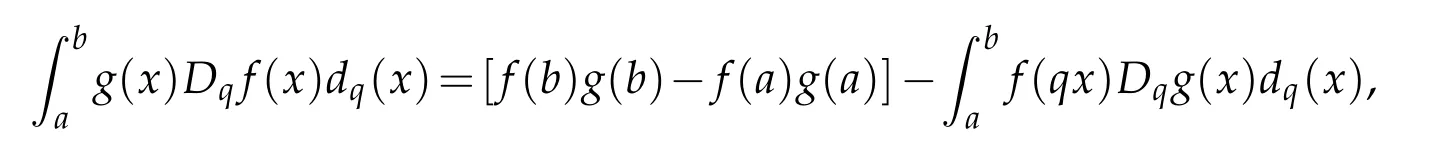
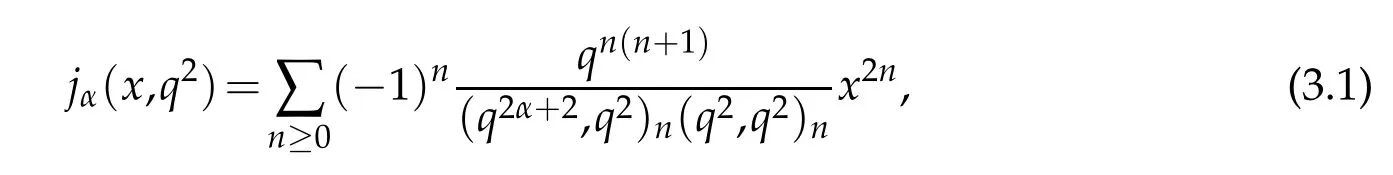
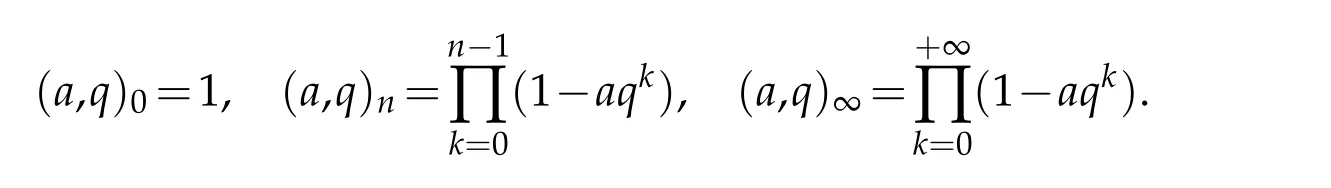
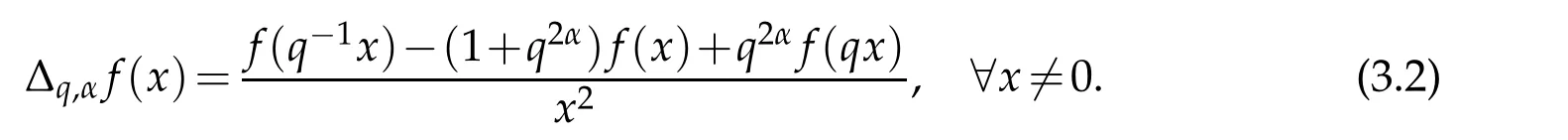
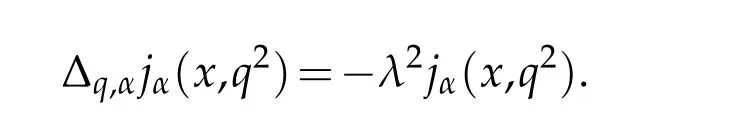
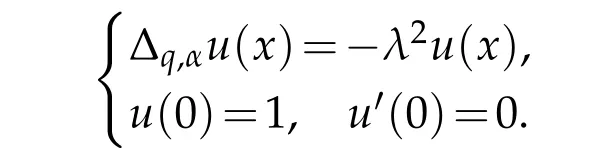
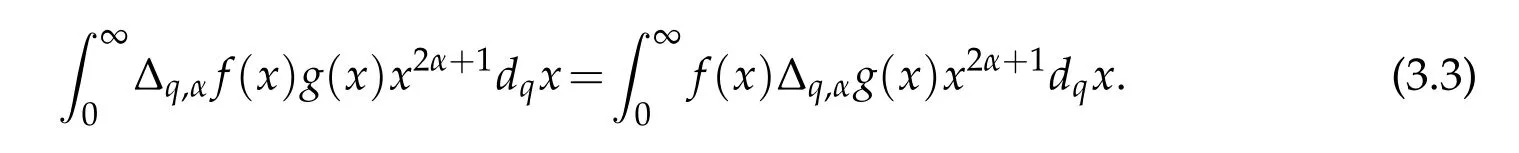
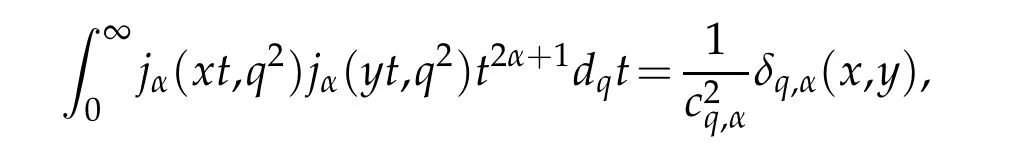

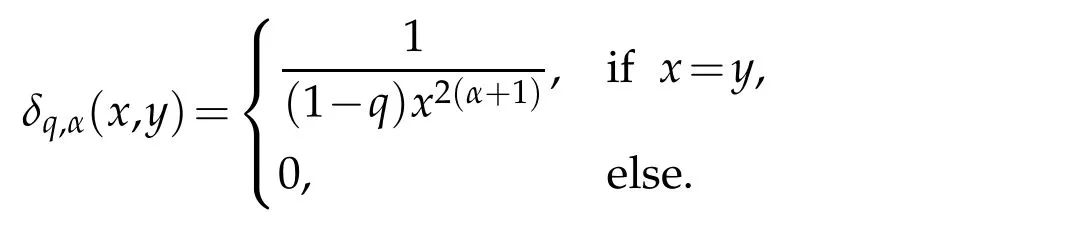
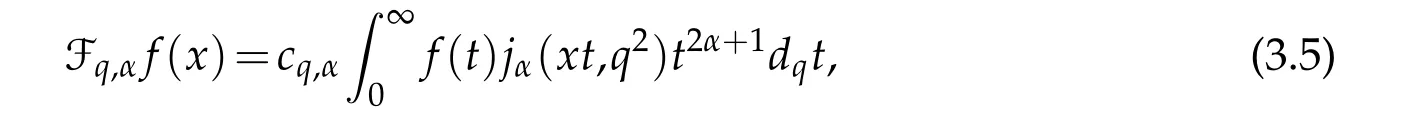
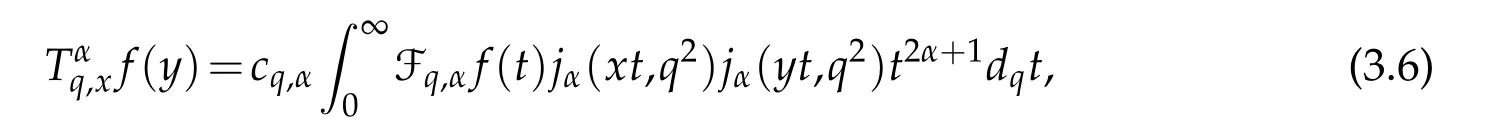
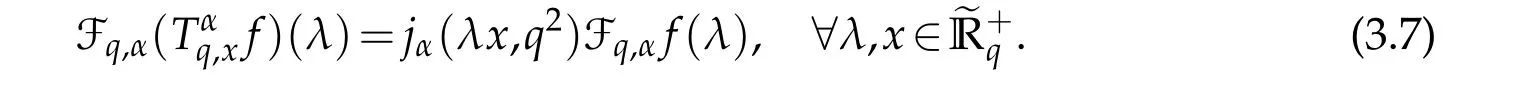
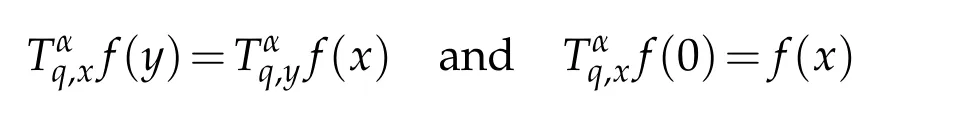
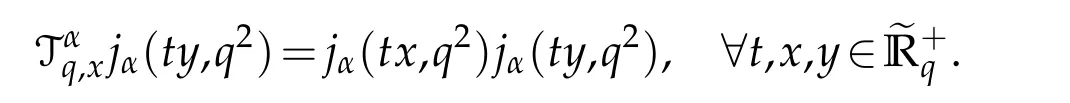
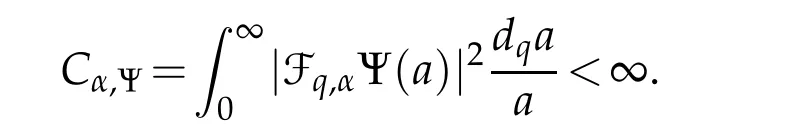
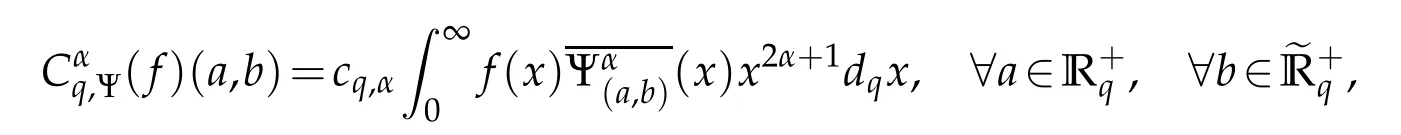
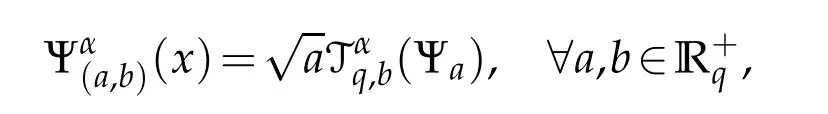
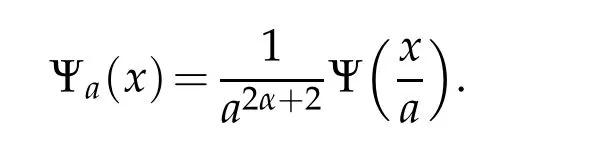
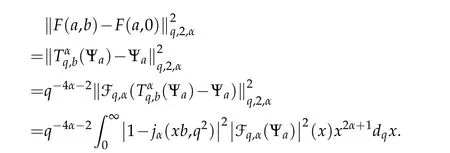
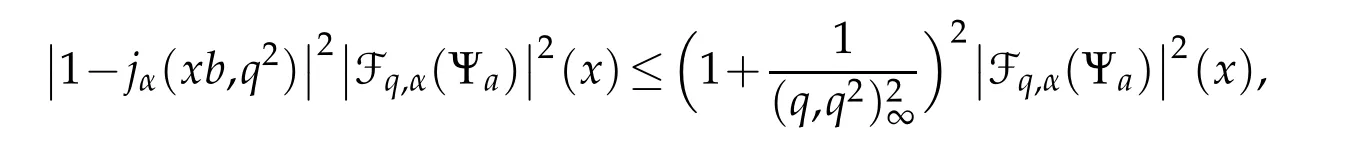
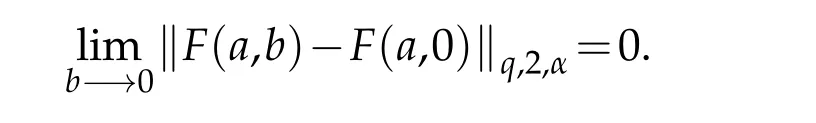
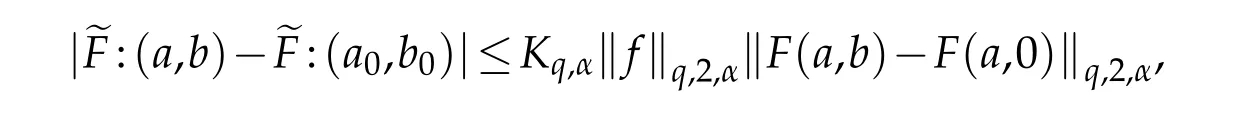
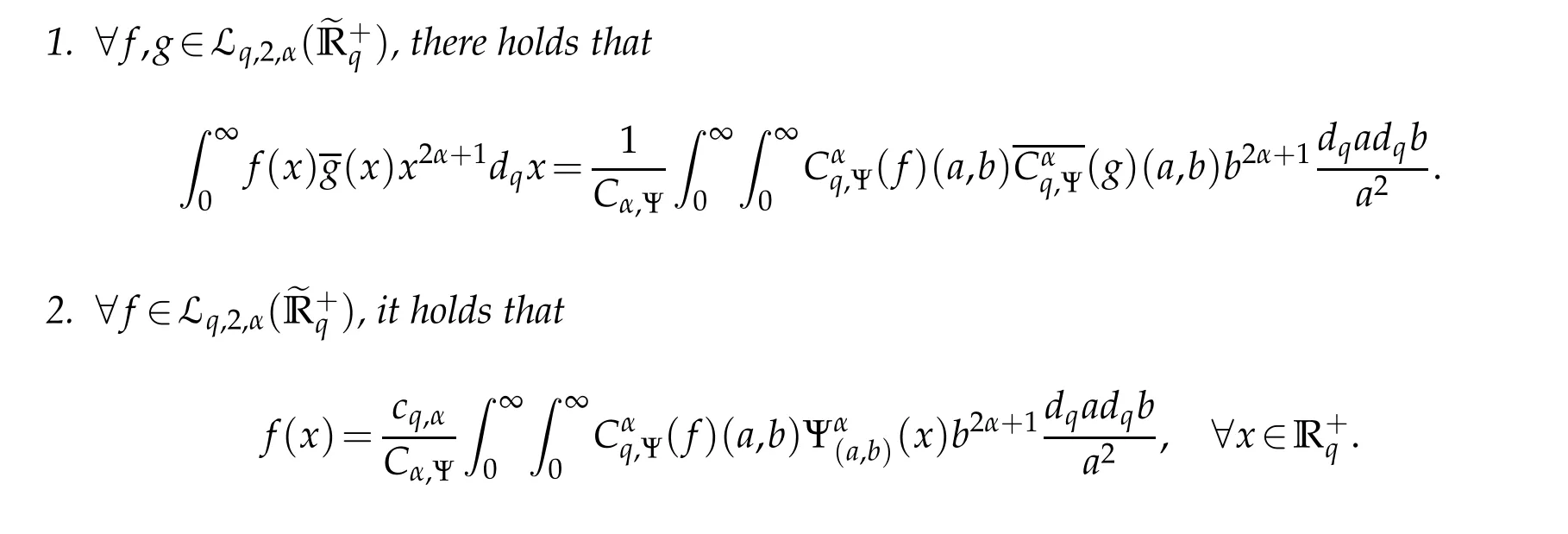
4 Generalized q-Bessel wavelets

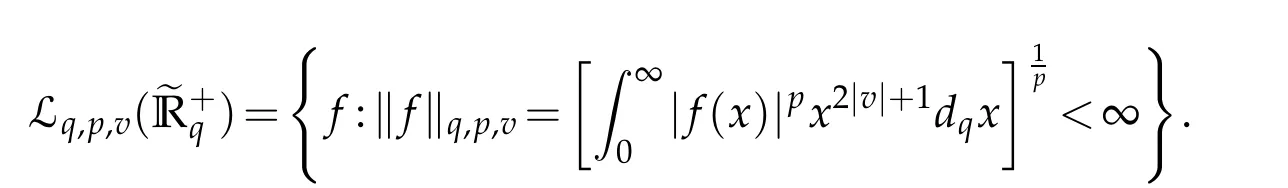
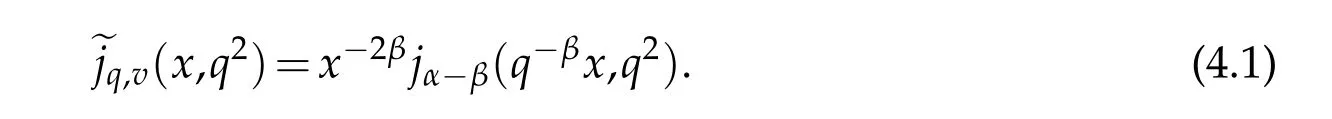
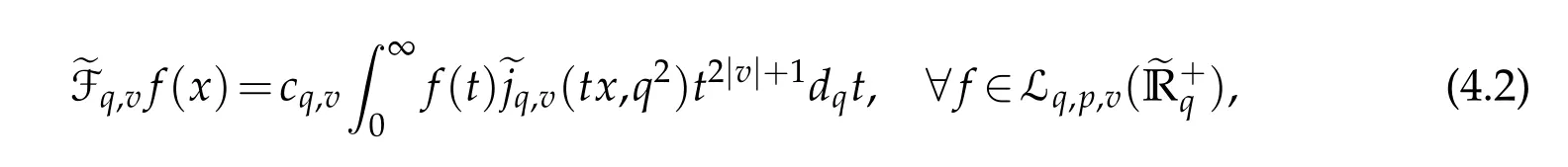
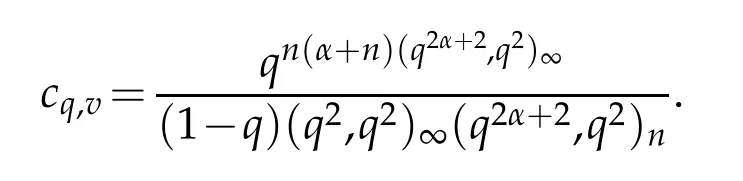
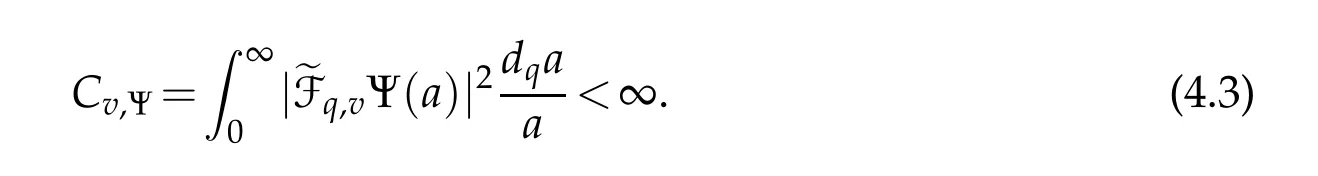
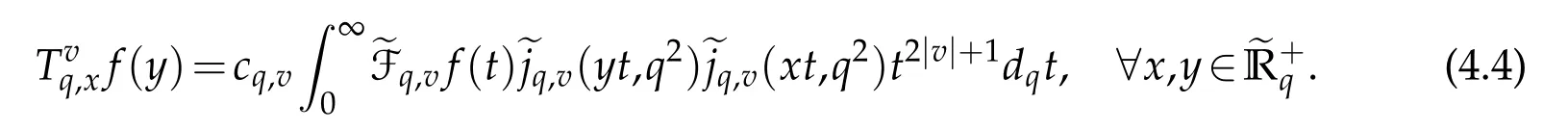
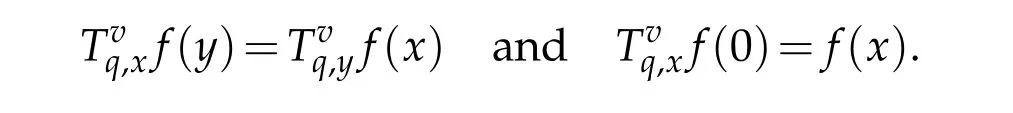
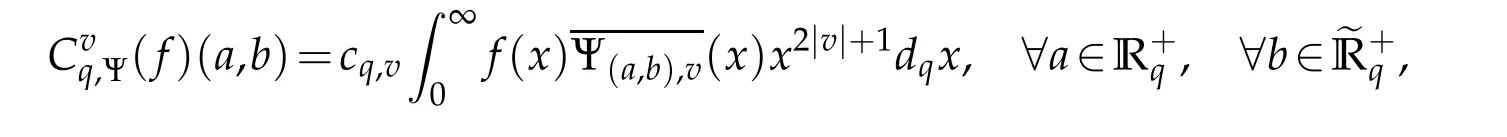
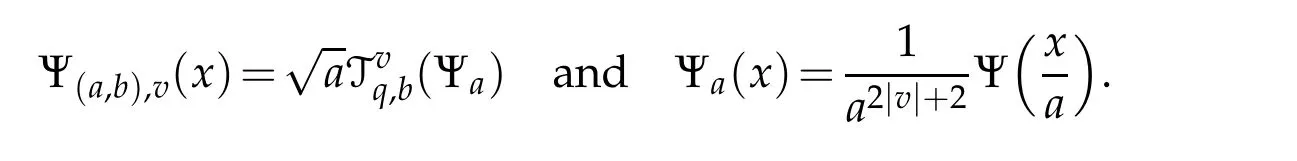
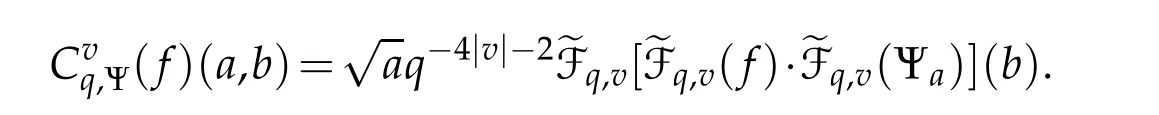
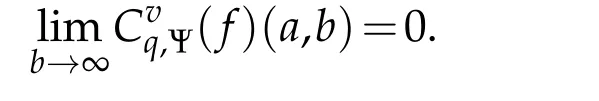
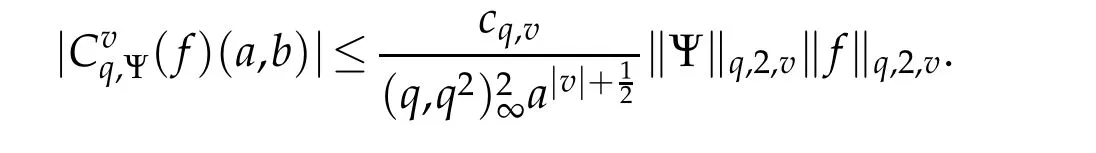
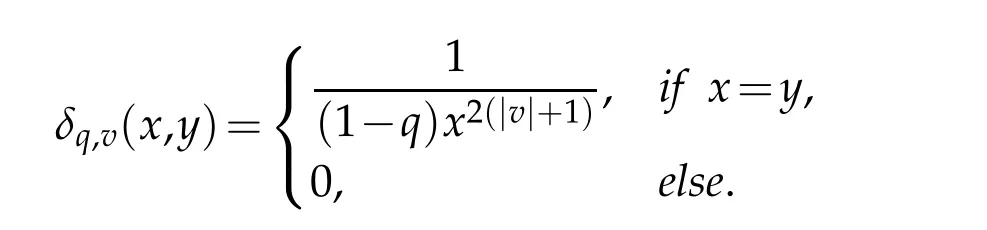
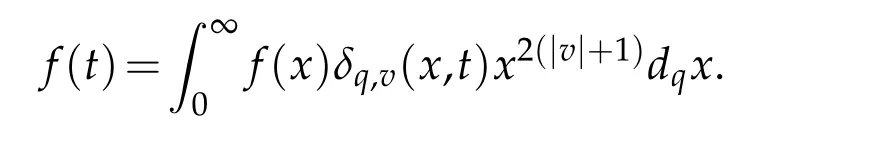
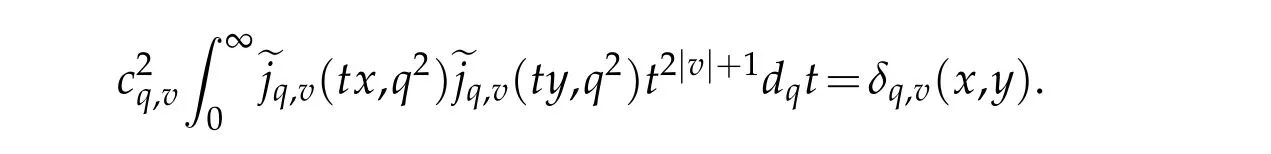
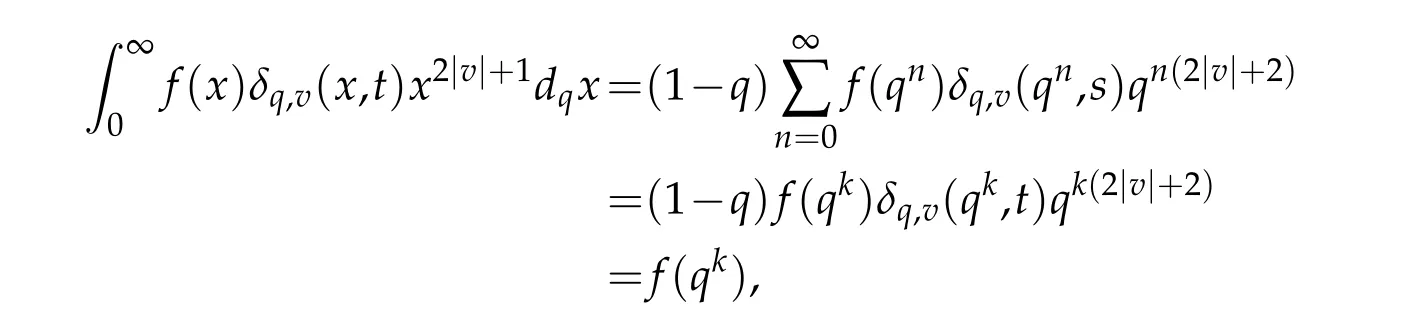
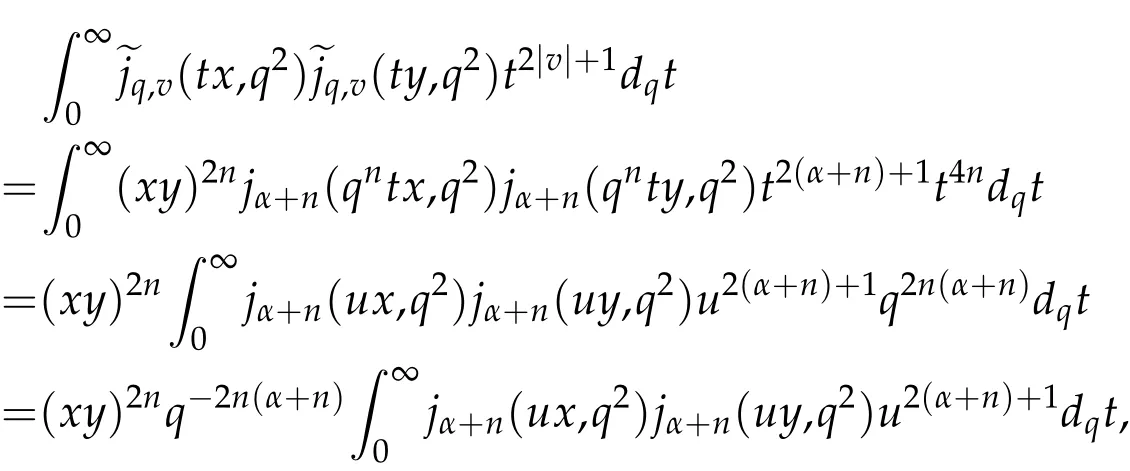
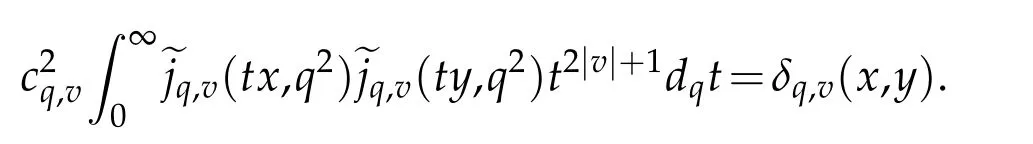
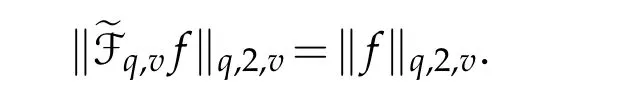
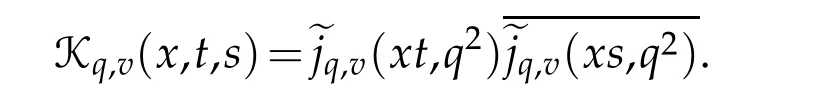
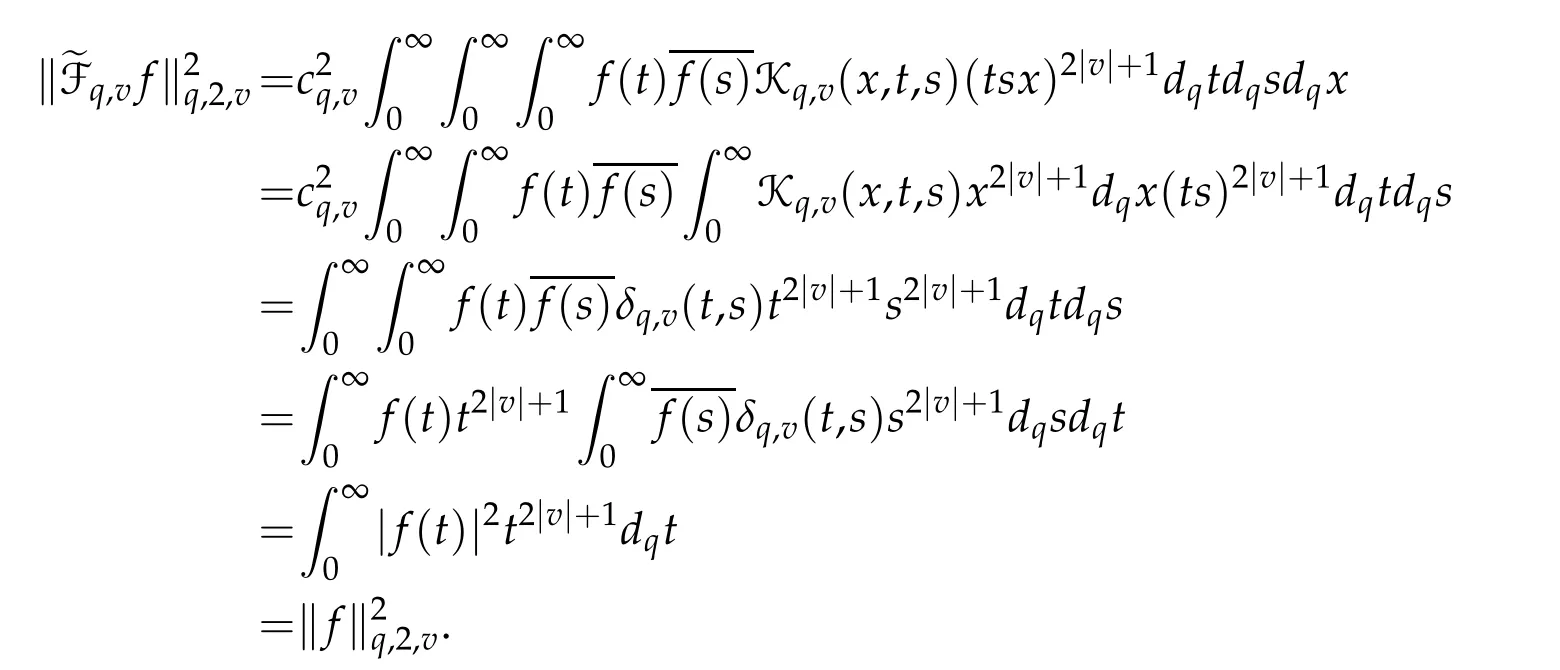
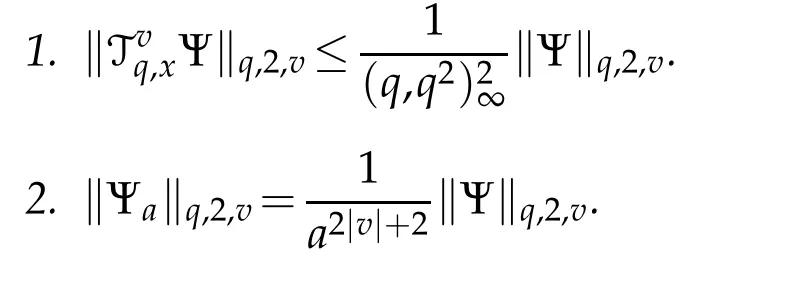
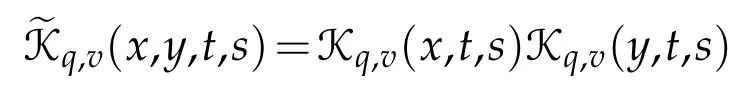
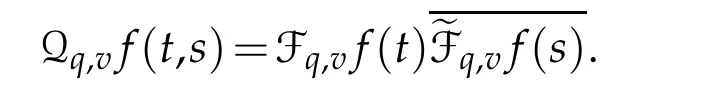
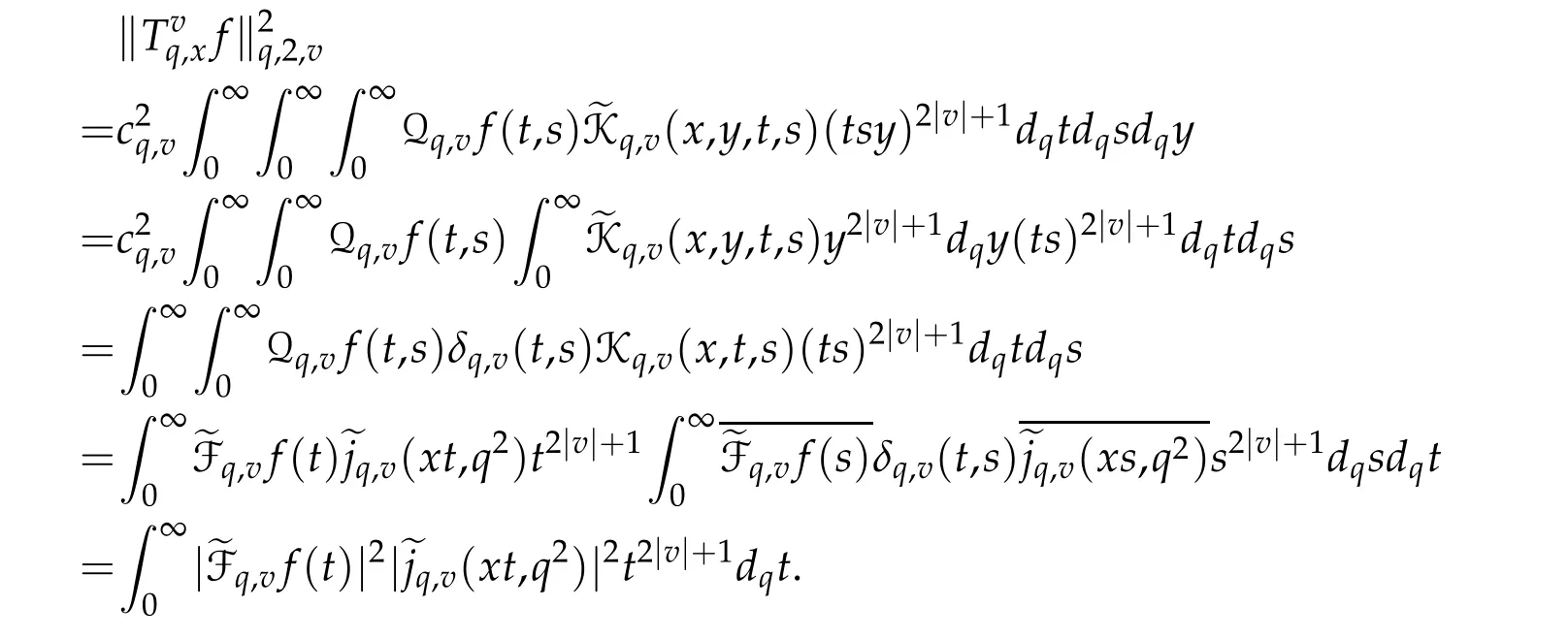
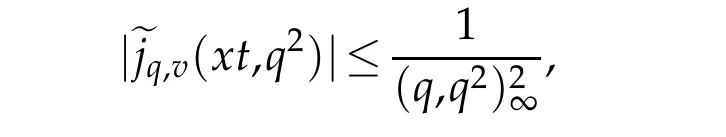
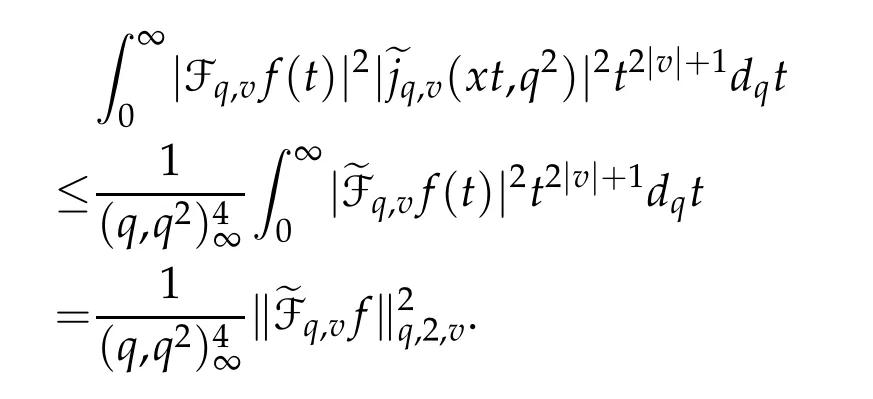
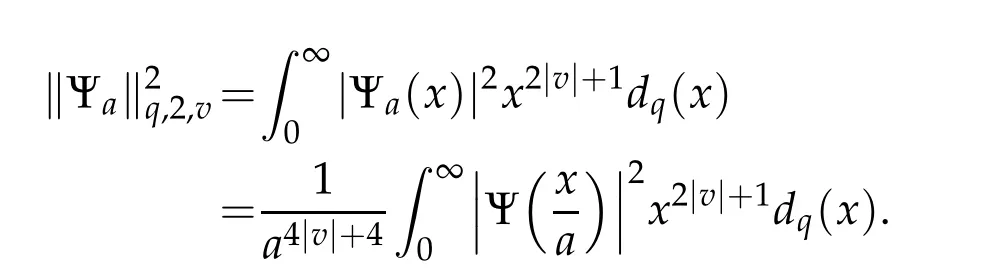
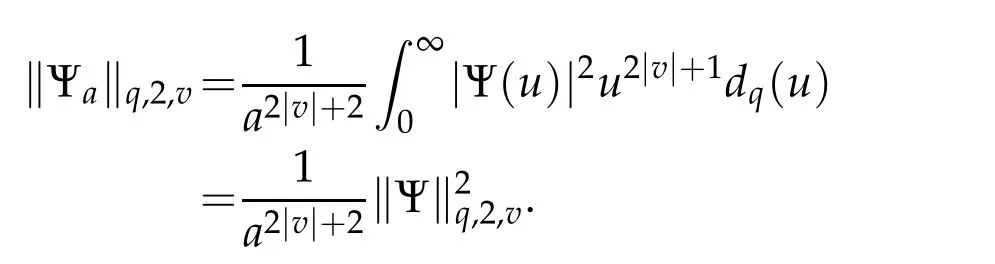
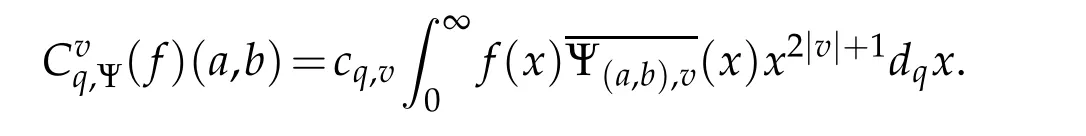
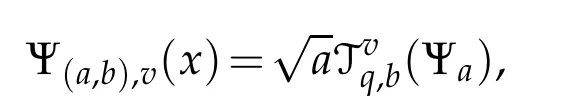
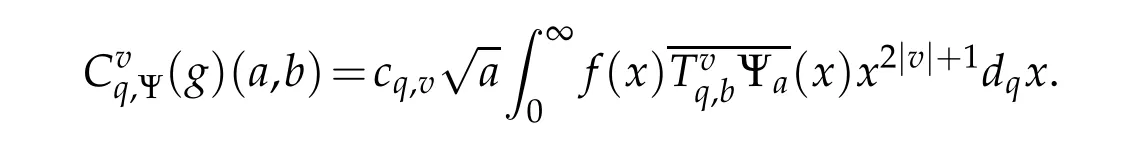
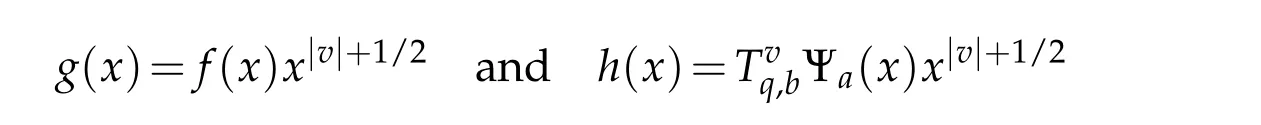
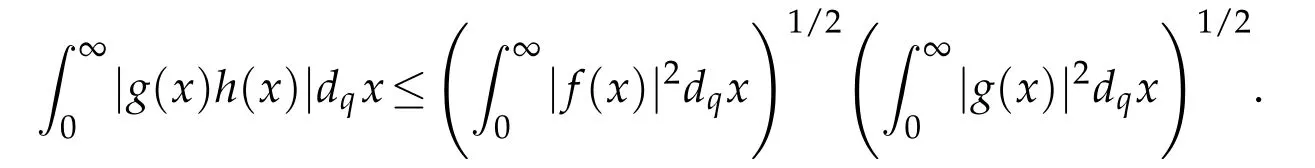
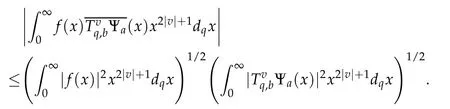
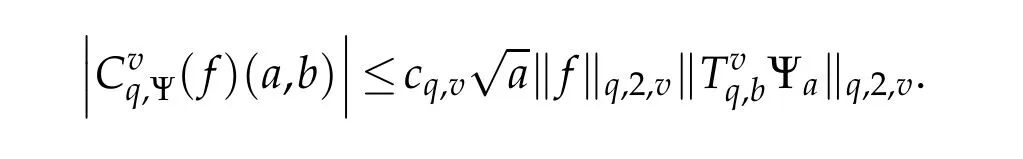
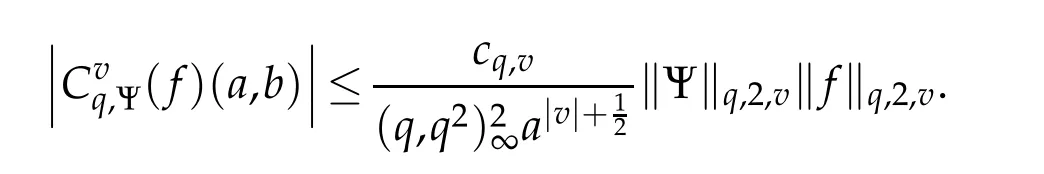
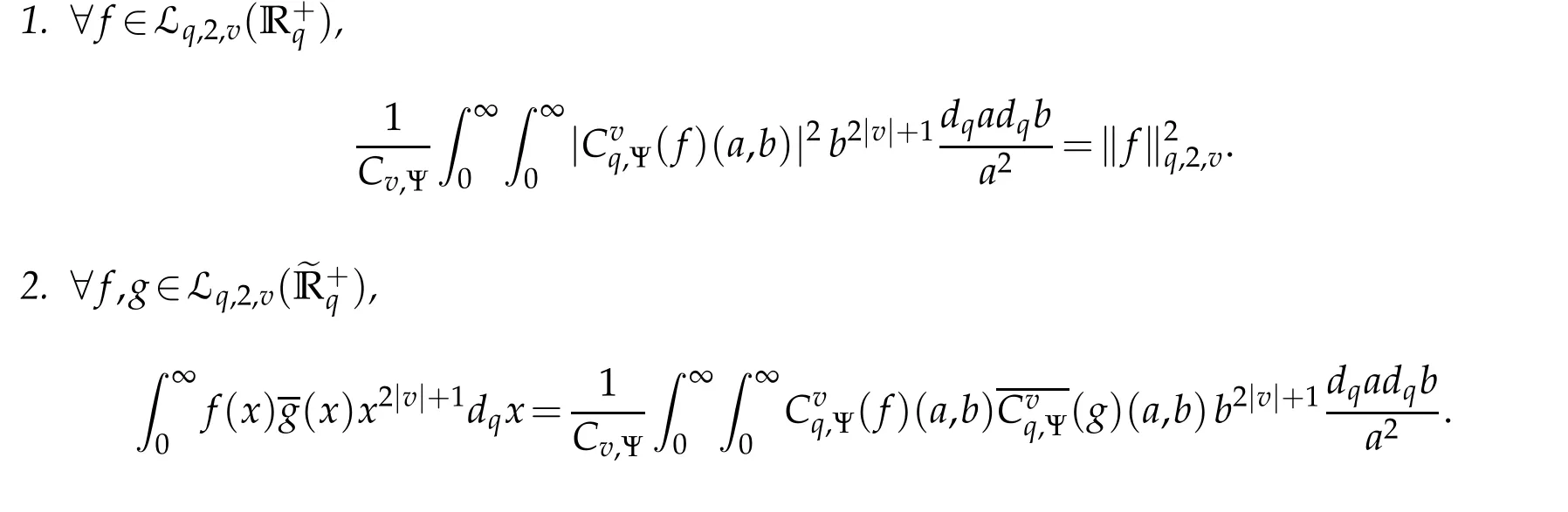
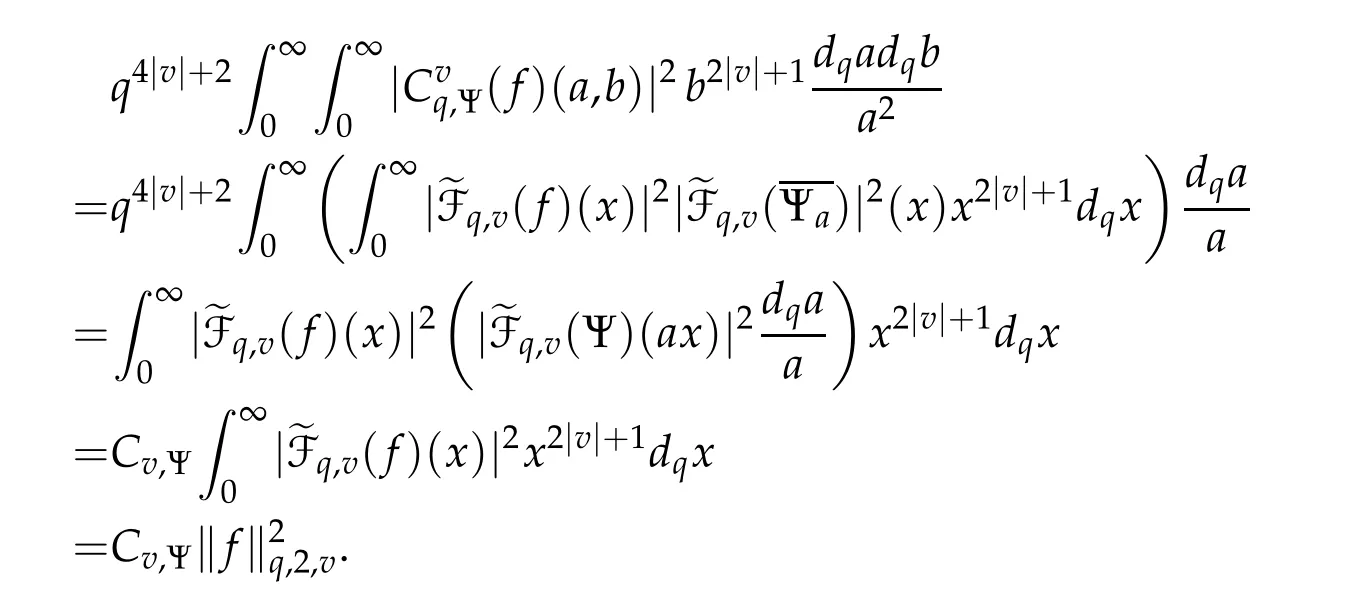
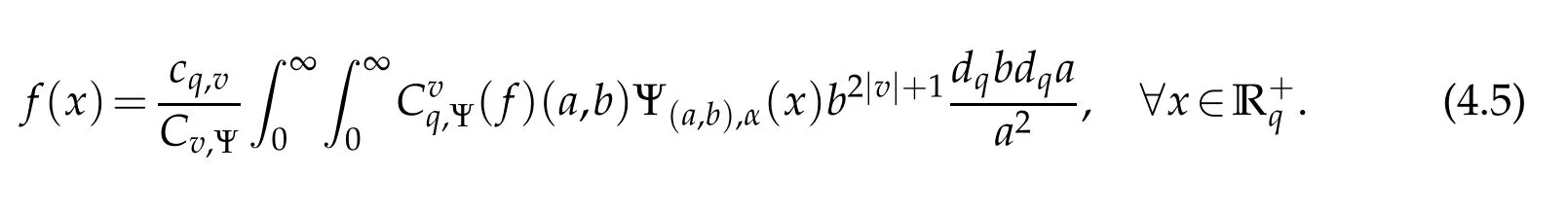
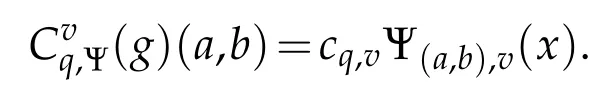
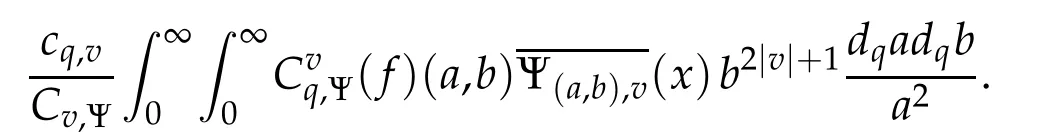
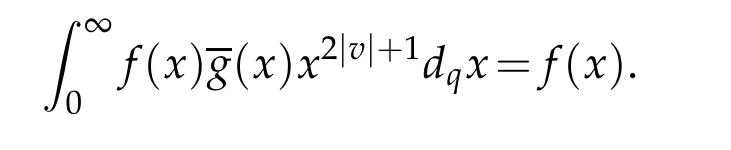
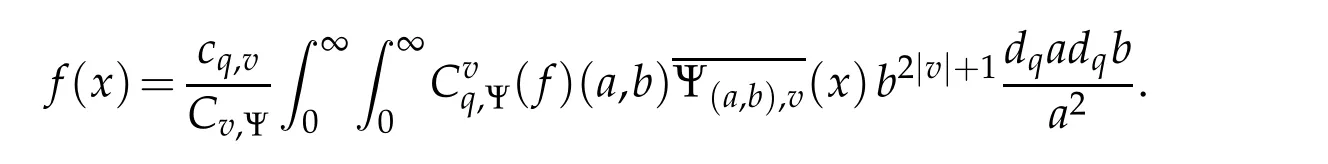
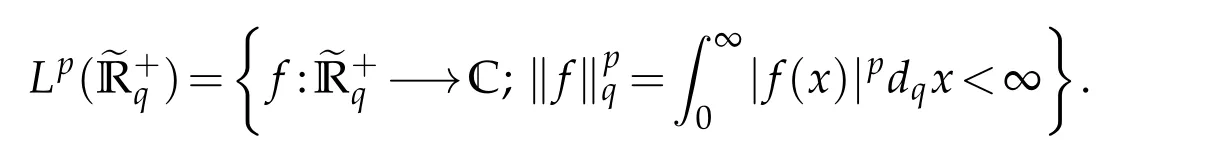
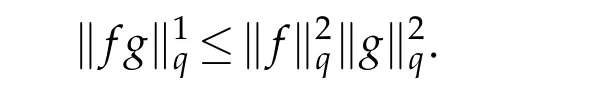
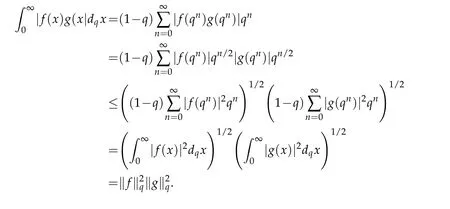
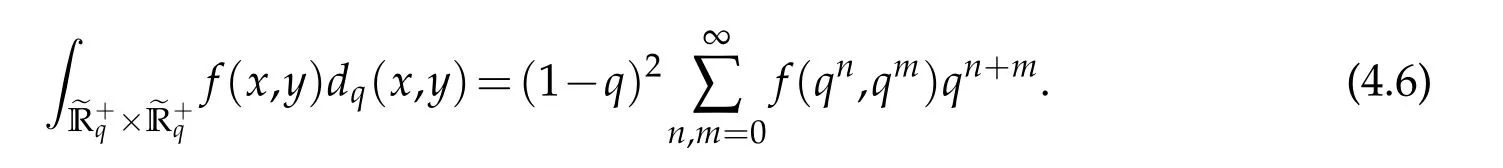
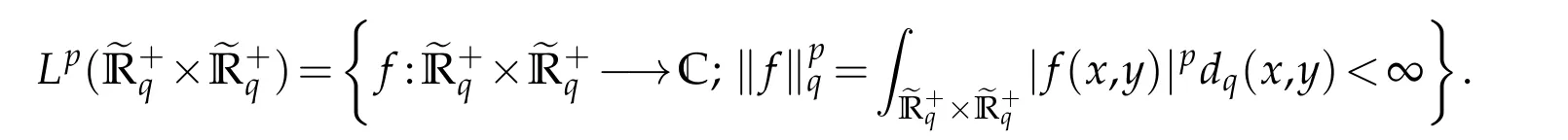
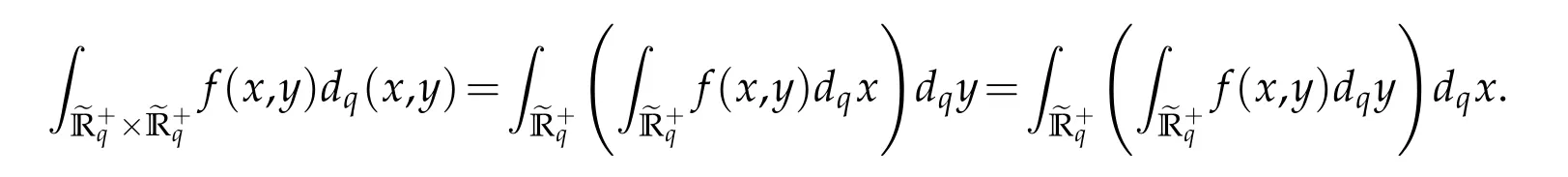
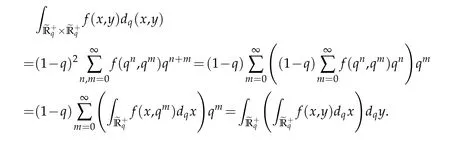
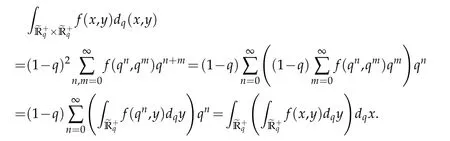
杂志排行
Analysis in Theory and Applications的其它文章
- On Weighted Lp−Approximation by Weighted Bernstein-Durrmeyer Operators
- A Struwe Type Decomposition Result for a Singular Elliptic Equation on Compact Riemannian Manifolds
- On an Axiomatic about Functional Means
- Commutators of Singular Integral Operators Related to Magnetic Schrdinger Operators
- Approximation for Certain Stancu Type Summation Integral Operator
- On Quasi-Chebyshevity Subsets of Unital Banach Algebras
