On an Axiomatic about Functional Means

Mustapha Rassouli,Mohamed Chergui and Abdellah Alla

1Department of Mathematics,Science Faculty,Taibah University,Al Madinah Al Munawwarah,P.O.Box 30097,Zip Code 41477,Saudi Arabia

2Department of Mathematics,Science Faculty,Moulay Ismail University,Meknes,Morocco

3Department of Mathematics,LaREAMA Lab,Centre Rgionaldes Mtiers del’Education et de la Formation(CRMEF),Kenitra,Morocco

4Department of Mathematics,Mohammed V University,Faculty of Sciences,LAMA-ANLIMAD,Rabat,Morocco

1 Introduction

For over the last centuries,the mean-theory has been the subject of intensive research.Scalar and operator means arise in various contexts and have multiple applications in theoretical point of view as well as in practical purposes.

In recent few years,extension of operator means from the case that the variables are positive linear operators to the case that the variables are convex functionals has been investigated by many authors.Such extensions were introduced in the sense that ifm(T,S)is an operator mean between two positive linear operatorTandSthen its extension F(f,g)for two functional variablesfandgsatisfies the following connection-relationship

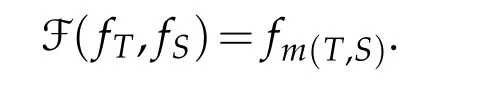
Here the notationfTrefers to the convex quadratic function generated by the positive linear operatorTacting on a Hilbert spaceHi.e.,fT(x)=(1/2)hTx,xi for allx∈H.

In the aim to recall some standard examples of functional means,we need some notation.LetHbe a complex Hilbert space andf:H−→R∪{−∞,∞}be a(convex)functional.We denote byf∗the conjugate offdefined through

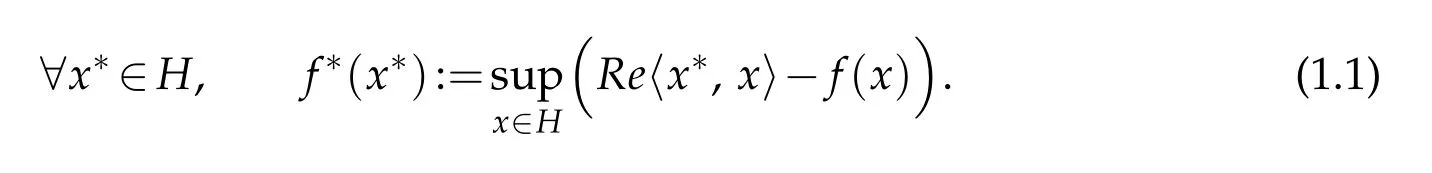
The arithmetic and harmonic functional means off,g:H−→R∪{∞}were introduced in[1,9,10]as follows

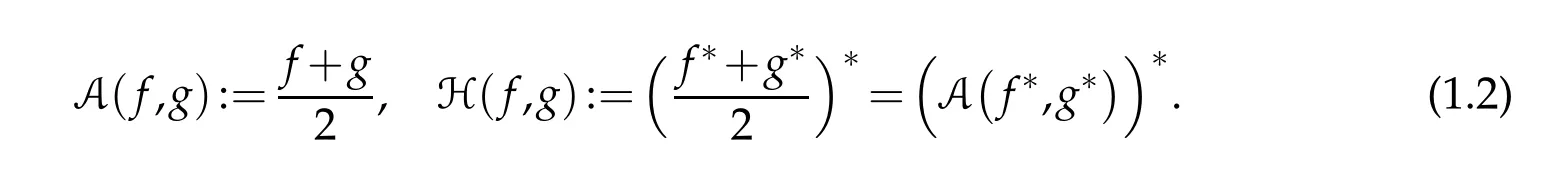
The geometric functional mean offandg,denoted here by G(f,g),was firstly introduced in[1]as the point-wise limit of an iterative process descending from the arithmetic and harmonic functional means.Since then some papers were written about G(f,g)in other points of view,see[4,8–10].Throughout this paper,we adopt as definition of G(f,g)the following one,see[9]for instance:

which,under convenient assumptions onfandg,is equivalent to that introduced in[1].

The above three functional means satisfy the next double inequality,see[9,10]

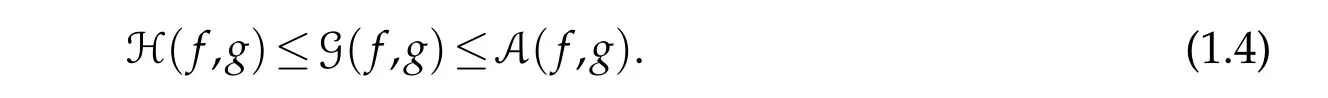
The logarithmic functional mean offandgwas defined by the author in[10]via the following relation:

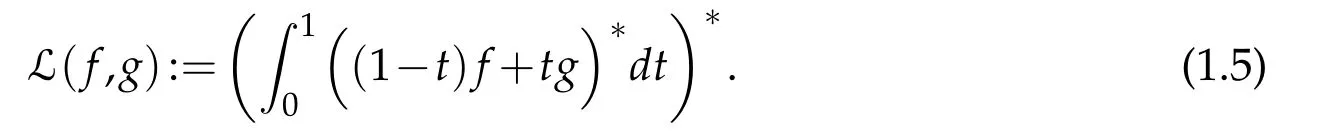
The logarithmic functional mean L(f,g)interpolates H(f,g)and A(f,g)in the sense that,see[10]

As far as we know,there is no inequality stated in the literature about comparison between G(f,g)and L(f,g).

For further details about the above functional means, and more other functional means,we indicate the references[4,8–10].We also refer the reader to[6]for some interesting discussion about the geometric functional mean as well as the construction of a parameterized algorithm extending that of G(f,g).

The fundamental goal of the present paper is to introduce a general definition for means involving(convex)functional argumentsfandg.In the case wherefandgare both quadratic functions generated by positive operators,we immediately obtain in a simple way the operator version of the present functional approach.

2 Basic notions and some results

We first recall some basic notions about convex analysis that will be needed later.For more details,we refer the reader to[2,3,7,12]for instance.

LetHbe a complex Hilbert space andf:H→=R∪{−∞,∞}be a functional(in short,we writef∈).The(extended)spaceof such functionals is equipped with the following partial order(so-called the point-wise order)

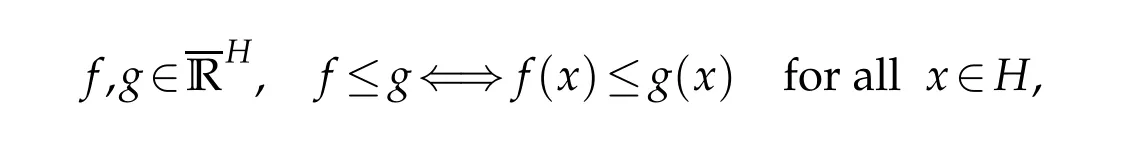
where we extend the structure of R to R∪{−∞,∞}by setting

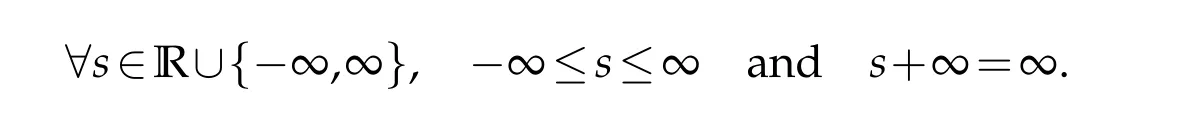
Since our involved functionals can take infinite values then the equalityf−f=0 does not always hold,since∞−∞=∞.For the same reason,the two inequalitiesf≤gandf−g≤0 are not always equivalent.

We say thatfis proper iffdoes not take the value−∞and is not identically equal to the value∞.The effective domain domfoff:H−→:=R∪{∞}is given by domf={x∈H,f(x)<∞}and its conjugatef∗is defined through(1.1).As it is well-known,f∗∗:=(f∗)∗≤f,f∗is always convex lower semi-continuous and,f≤gimpliesg∗≤f∗,for all functionalsf,g∈H.We denote by Γ0(H)the cone of all convex lower semicontinuous proper functionals.It is well known thatf∈Γ0(H)if and only iff∗∗=f.

Let B(H)be the space of bounded linear operators defined fromHinto itself.As usual,a self-adjoint operatorT∈B(H)is positive(denotedT≥0)if hTx,xi≥0 for allx∈H.The set of all(self-adjoint)positive invertible operatorsT∈B(H)(in shortT>0)will be denoted by B+∗(H).ForT,S∈B(H),we writeT≤Sif and only ifTandSare self-adjoint andS−T≥0.

With this,we state the following example which is of interest.

Example 2.1.LetT,Sbe two positive linear operators ofHandfT,fStheir generated quadratic functionals,i.e.,fT(x)=(1/2)hTx,xifor everyx∈H.Then we have:

(i)fT±fS=fT±Sand,fT=(≥≤)fSif and only ifT=(≥≤)S.

(ii)domfT=HandfT∈Γ0(H).

(iii)If moreoverTis invertible thenfor allx∈H.We then write

Proposition 2.1.Letf:H−→R∪{∞}.Then there hold:

(i)Iffis not identically equal to∞thenf∗>−∞i.e.,f∗does not take the value−∞.

(ii)Iffis convex lower semi-continuous and not identically equal to ∞ then so isf∗.That is,f∈Γ0(H)impliesf∗∈Γ0(H).

Proof.(i)By hypothesis,there isx0∈Hsuch thatf(x0)<∞.Otherwise,from(1.1)we deduce,for everyx∗∈H,

(ii)In factf∗is always convex lower semi-continuous evenfis not.We have only to show thatf∗is not identically equal to∞.For this,see(see[2],Proposition I.9,page 9)for instance,where the desired result is established by using the geometric version of the celebrate Hahn-Banach theorem.

Before giving another result,we need more notations.We define

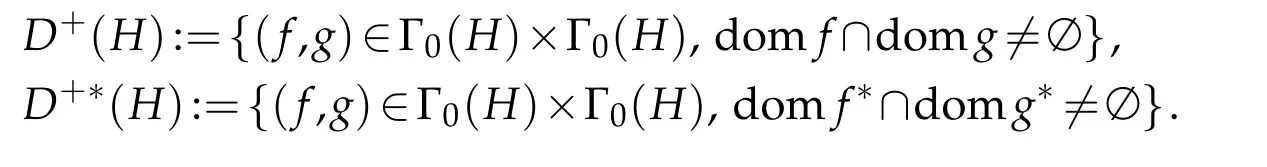
Obviously,D+(H)andD+∗(H)are two nonempty sub-cones of the product-cone Γ0(H)×Γ0(H),with the next implications

Further,it is easy to see that(fT,fS)∈D+(H)∩D+∗(H)for allT,S∈B+∗(H).

We now may state the following result.

Proposition 2.2.(i)Letf,g∈D+(H).Then A(f,g)∈Γ0(H).

(ii)Letf,g∈D+∗(H).Then H(f,g)∈Γ0(H),G(f,g)∈Γ0(H)and L(f,g)∈Γ0(H).

Proof.(i)Assume thatf,g∈D+(H).It is clear that A(f,g)is convex,lower semicontinuous and A(f,g)>−∞.Since domf∩domg6=∅ then there isx0∈Hsuch thatf(x0)<∞andg(x0)<∞.We then deduce A(f,g)(x0)<∞and the desired result follows.

(ii)By the previous proposition,we havef∗,g∗∈Γ0(H)and by the above(i)we obtain A(f∗,g∗)∈Γ0(H).Again,by the same above proposition we deduce that H(f,g):=?A(f∗,g∗)?∗∈Γ0(H).

The fact that G(f,g)∈Γ0(H)and L(f,g)∈Γ0(H)follow immediately from(1.4)and(1.6),respectively.The proof is so complete.

Proposition 2.3.Letf,g,h,k:H−→R∪{∞}be four given functionals.Then we have:

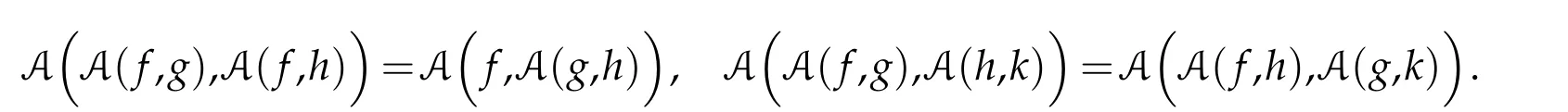
Furthermore,

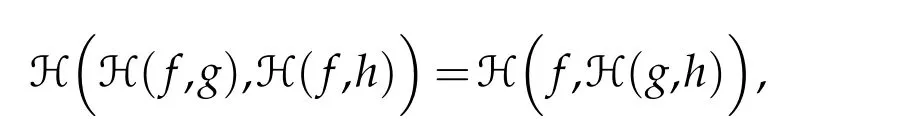
provided that(f,g),(f,h),(g,h)∈D+∗(H),and

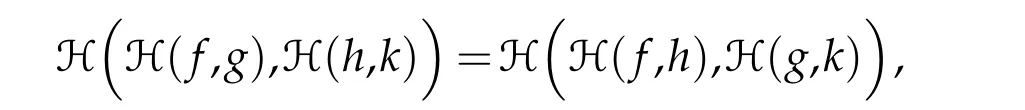
provided that(f,g),(h,k),(f,h),(g,k)∈D+∗(H).

Proof.The proof of the first equality and that of the second one are simple and comes from the fact that A(f,g)has a linear affine character with respect to its variablesfandg.We will prove the third equality.Indeed,by definition of H we have

Sincef,g∈Γ0(H)thenf∗,g∗∈Γ0(H),too.According to the previous we then deduce A(f∗,g∗)∈Γ0(H).Similarly,we prove that A(f∗,h∗)∈Γ0(H).It follows that

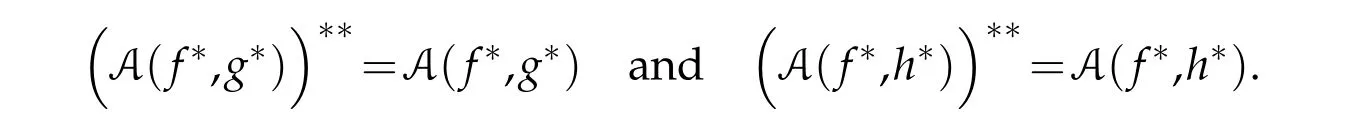
With this,we can write

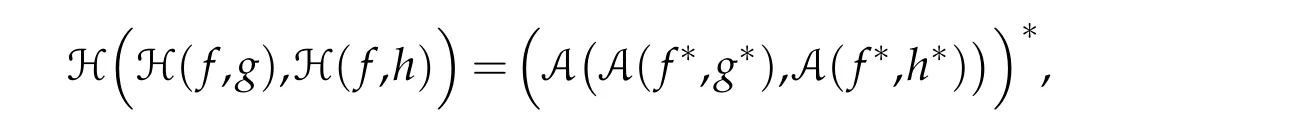
which,with the above first equality,yields

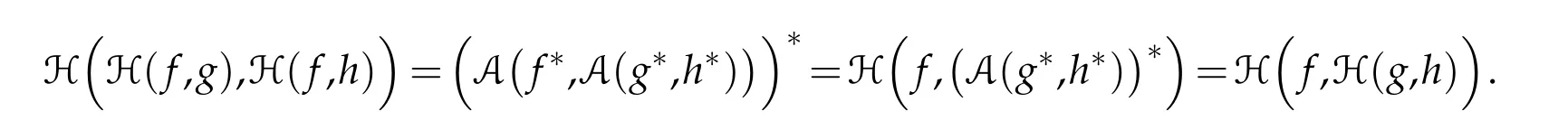
The fourth equality can be proved in a similar manner as the third one.

Before stating another result,we introduce more notions as recited in the following:

Definition 2.1.Let(fn)be a sequence of functionals defined fromHinto R∪{∞}:

(i)We say that(fn)is point-wisely increasing(in shortp-increasing)if for alln,fn≤fn+1for the point-wise order.

(ii)We say that(fn)is point-wisely convergent(in shortp-convergent)if there is a functionalf:H−→R∪{−∞,∞}such that limn↑∞fn(x)=f(x)for allx∈H.

The following example,which illustrates the above definition,is of interest.

Example 2.2.Letfn(x)=(1/2)hTnx,xi for allx∈H,where(Tn)is a sequence of self adjoint linear operators.Then:

(i)(fn)isp-increasing(resp.p-decreasing)if and only if(Tn)is increasing(resp.decreasing)for the Lowner order.

(ii)(fn)p-converges if and only if for allx∈H,limn↑∞hTnx,xi=f(x)for some functionalf.If moreover,fis with finite values then there exists a self-adjoint linear operatorTsuch thatf=fT.With this,(fn)p-converges tofif and only if(Tn)converges quadratically toT.Further,it is well-known that,ifTn≥Tthen,(Tn)converges quadratically toTif and only if(Tn)converges strongly(i.e.,in norm)toT.

Now,we are in position to state our desired result recited as follows.

Proposition 2.4.Let(fn)be ap-decreasing sequence of functionalsp-converging tof.

Thenp-converges increasingly tof∗.

Proof.First,remark thatisp-increasing sinceisp-decreasing.The fact that(fn)p-converges decreasingly tofis equivalent tof=limwhere the infimum is taken here for the point-wise order.We wish to establish thatWe have,for allx∗∈H,

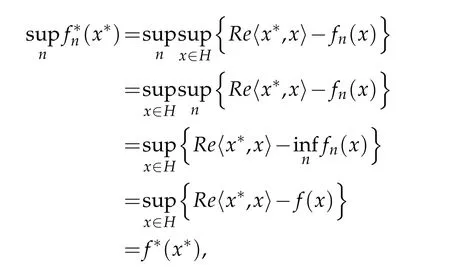
which is the desired result,so completes the proof of the proposition.

3 Axiomatic theory about functional means

This section displays an axiomatic study about functional means.We first recall the following,see[11].

Definition 3.1.Let M:B+∗(H)×B+∗(H)−→B+∗(H)be a binary map satisfying the following list of assertions:

(o1)M(T,T)=Tfor allT∈B+∗(H);

(o2)M(T,S)=M(S,T)for allT,S∈B+∗(H);

(o3)M(λT,λS)=λM(T,S)for allT,S∈B+∗(H)and every real numberλ>0;

(o4)For allT1,T2,S1,S2∈B+∗(H)such thatT1≤T2andS1≤S2we have M(T1,S1)≤M(T2,S2).In this case,we say that M is a monotone operator mean.

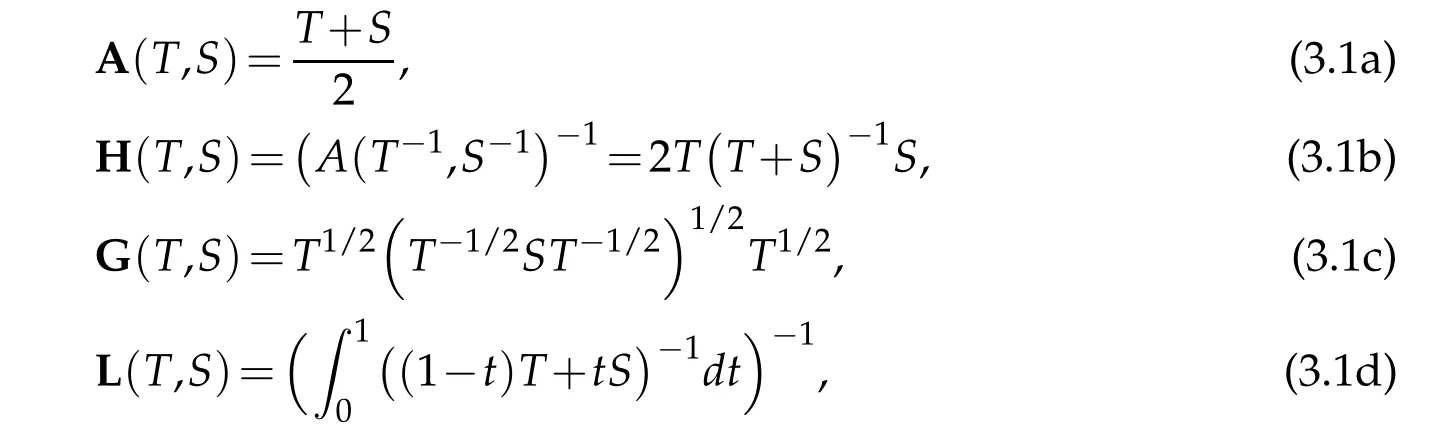
The standard examples of monotone operator means are the following:and are known as the arithmetic,harmonic,geometric and logarithmic operator means,respectively.For further examples about monotone operator means(not needed here)we refer the reader to[11]and the related references cited therein.As pointed out in[11],monotone operator means operator means adopted here include those of Kubo-Andoones,[5].The above four operator means satisfy the following chain of inequalities

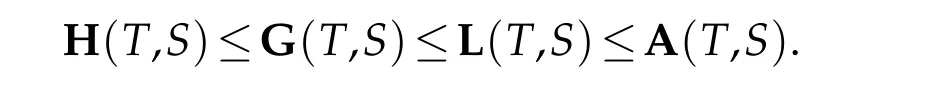
In the scalar case(i.e.,dim H=1)they are,respectively,reduced to the so-called scalar means,namely

for all real numbersa>0,b>0.

Now,we are in position to state our adopted definition about functional means recited as follows.

Definition 3.2.By functional mean we understand a binary map F between Γ0(H)-functionals satisfying the following requirements:

(f1)F(f,f)=ffor allf∈Γ0(H);

(f2)F(f,g)=F(g,f)for allf,g∈Γ0(H);

(f3)F(t.f,t.g)=t.F(f,g)for allf,g∈Γ0(H)and each real numbert>0;

(f4)F(f,g)is point-wisely increasing inf(and ing),that is for allf1,f2∈Γ0(H)such thatf1≤f2and everyg∈Γ0(H),we have F(f1,g)≤F(f2,g);(of)For allT,S∈B+∗(H),we have

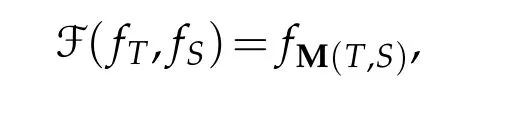
where M is a monotone operator mean.In this case,we say that F is the M-functional mean.

Obviously,the set of all functional means is a convex cone.Otherwise,it is easy to see that the class of functional means adopted here include that introduced by Fujii in[4].

The standard examples of functionals means known in the literature are A(f,g),H(f,g),G(f,g)and L(f,g)previously defined.These are known as the arithmetic,harmonic,geometric and logarithmic functional means,respectively,since they satisfy(following the above requirement(of))

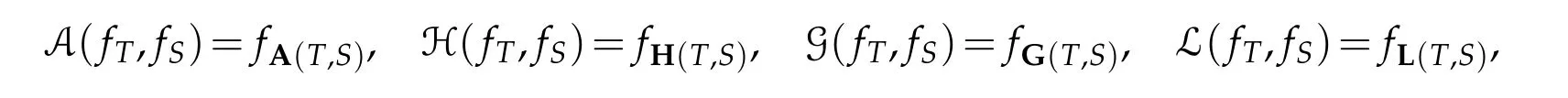
for allT,S∈B+∗(H),where A(T,S),H(T,S),G(T,S)and L(T,S)are defined by(3.1a),(3.1b),(3.1c)and(3.1d),respectively.

The following remark is of interest.

Remark 3.1.The assertions(f1)-(f4),for defining a functional mean,were put by analogy with(o1)-(o4),respectively.However,the assertion(of),giving a connection relationship between functional mean and its related operator mean,is here taken as primordial condition.This is in the aim to have nice properties and interesting examples of functional means.The following counter-example explains more precisely this latter situation.

Example 3.1.Letf,g∈ Γ0(H)and consider the maps(f,g)7−→ inf(f,g)and(f,g)7−→sup(f,g),where the infimum and the supremum are taken for the point-wise order.It is easy to see that these two functional-maps satisfy the requirements(f1)-(f4).However,they do not satisfy(of)in general,because the algebra B(H)is not totaly ordered whendim H≥ 2.In another way,(f,g)7−→ inf(f,g)and(f,g)7−→ sup(f,g)are in general not functional means.

Now,the following result may be stated.

Proposition 3.1.Let F be a functional mean.Then the following functional-inequalities

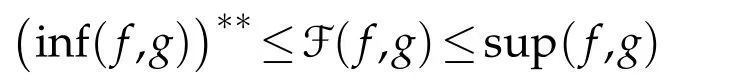
hold true for all(f,g)∈D+(H).

Proof.Let(f,g)∈D+(H).It is not hard to see that?inf(f,g)?∗∗and sup(f,g)belong to Γ0(H).Now,writing

we then deduce,by(f4)and(f1),the desired result after a simple manipulation.

As it is well-known,even iff,g∈Γ0(H)are convex,inf(f,g)is not convex in general,and so

We now end this section by stating the following result.

Proposition 3.2.Let Fnbe a sequence of functional means.Assume that,for allf,g∈Γ0(H),we have

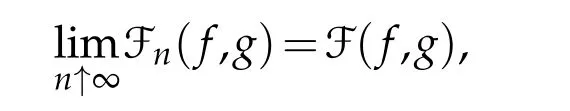
where the limit is taken for the point-wise convergence.Then F is a functional mean.

Proof.It is easy to verify that,if Fnsatisfies(f1)-(f4)for eachn,then so is F.Only the requirement(of)needs some detail.

So,let us prove that F(fT,fS)=fM(T,S),for some monotone operator mean M.By virtue of our assumption we can write for all integern,Fn(fT,fS)=fMn(T,S)with Mnis a monotone operator mean.Since(Fn(fT,fS))is point-wisely convergent we can then put limfMn(T,S)=f(T,S).Now,according to Example 2.2(ii)we can statef(T,S)=fM(T,S)and consequently F(fT,fS)=fM(T,S).We now need to show that M is a monotone operator mean,i.e.,M satisfies the assertions(o1)-(o4)of Definition 3.1.This can be checked in an elementary way.We omit the details which are very simple.

References

[1]M.Atteia and M.Raıssouli,Self dual operators on convex functionals,geometric mean and square root of convex functionals,J.Convex Anal.,8(1)(2001),223–240.

[2]H.Brzis,Analyse Fonctionnelle,Theory et Applications,Masson,1986.

[3]I.Ekeland and R.Temam,Convex Analysis and Variational Problems,SIAM,1999.

[4]J.I.Fujii,Kubo-Ando theory of convex functional means,Sci.Math.Japon.,7(2002),299–311.

[5]F.Kubo and T.Ando,Means of positive linear operators,Math.Ann.246(1980),205–224.

[6]S.Kum and Y.Lim,A geometric mean of parameteized arithmetic and harmonic means of convex functions,Abstract Appl.Anal.,(2012),836804.

[7]P.J.Laurent,Approximation et Optimisation,Hermann,1972.

[8]M.Rassouli and M.Chergui,Arithmetico-geometric and geometrico-harmonic means of two convex functionals,Sci.Math.Japonicae,55(3)(2002),485–492.

[9]M.Rassouli and H.Bouziane,Arithmetico-geometrico-harmonic functional mean in convex analysis,Ann.Sci.Math.Quebec,30(1)(2006),79–107.

[10]M.Rassouli,Logarithmic functional mean in convex analysis,J.Ineq.Pure Appl.Math.,10(4)(2009).

[11]M.Rassouli,Stable and stabilizable means involving linear operator arguments,Linear and Multilinear Algebra,62(9)(2014),1153–1168.

[12]E.Zeidler,Nonlinear Functional Analysis and Its Applications III,Springer-Verlag,1984.