Commutators of Singular Integral Operators Related to Magnetic Schrdinger Operators
2018-05-24WanqingMaandYuLiu
Wanqing Ma and Yu Liu
School of Mathematics and Physics,University of Science and Technology Beijing,Beijing 100083,China
1 Introduction
Letbbe a locally integrable function on RnandTbe a linear operator.For a suitable functionf,the commutator is defined by[b,T]f=bT(f)−T(bf).It is well known that Coifman,Rochberg and Weiss[3]proved that[b,T]is a bounded operator onLpfor 1 Furthermore,Lu,Wu and Yang studied the boundedness properties of the commutator[b,T]on the classical Hardy spaces whenb∈Lipα(Rn)in[12]. In recent years,more scholars pay attention to the boundedness of the commutators[b,T]whenTare the singular integral operators associated with the Schrdinger operator(cf.[1,6–11]).When the potentialVsatisfies the weaker condition,the operatorTmay not be a Calder´on-Zygmund operator.In this paper we focus on the boundedness of the commutators[b,T]whenTare the singular integral operators associated with the magnetic Schrdinger operator based on the research in[5]and[16]. Consider a real vector potential~a=(a1,···,an)and an electric potentialV.In this paper,we assume that LetLk=∂/∂xk−iak.We adopt the same notation as in[5]and define thesesquilinear form Qby with domain It is known thatQis closed and symmetric.So the magnetic Schrdinger operatorAis a self-adjoint operator associated withQ. The domain ofAis given by andAis formally given by the following expression orA=−(∇−)·(∇−)+V,whereis the adjoint operator ofLk.Fork=1,···,n,the operatorsLkA−1/2andV1/2A−1/2are called the Riesz transforms associated withA.Moreover,it was proved in[14]that for eachk=1,···,n,the Riesz transformLkA−1/2andV1/2A−1/2are bounded onLp(Rn)for all 1 Furthermore,in[5]Duong and Yan proved that the commutators[b,V1/2A−1/2]and[b,LkA−1/2]are bounded onLpfor 1 See also Shen’s result in[15]forLp-boundedness of singular integral operators related to the magnetic Schrdinger operator,which is different from the operatorsLkA−1/2andV1/2A−1/2.Recently,D.Y.Yang in[16]has proven that fork∈{1,···,n},the commutators[b,LkA−1/2]are bounded fromLp(Rn)toLq(Rn)with 1/p−1/q=α/n,whereb∈Lipα(Rn).Inspired by[5]and[16],the purpose of this paper is to study the boundedness of commutator[b,V1/2A−1/2]with a functionbin the Lipschitz space Lipα(Rn),α∈(0,1). We are now in a position to give our main result,which will be proven in the next section. Theorem 1.1.Let α∈(0,1),p,q∈(1,2]with1/p−1/q=α/n.Assume that b∈Lipα(Rn).Then the commutator[b,V1/2A−1/2]is bounded from Lp(Rn)to Lq(Rn). In this section,we adopt the method in[16]to prove Theorem 1.1.Firstly,we begin with the sharp maximal functionestablished in[13].For anyf∈Lp(Rn),p∈[1,∞),the sharp maximal functionassociated with the semi group{e−tA}is given by whererBis the radius of the ballBandtB:= Lemma 2.1.Let p∈(1,∞).There exists a positive constant Cpsuch that for all f∈Lp(Rn), Proofof Theorem 1.1.Now,we prove the boundedness of the commutator[b,V1/2A−1/2]in Theorem 1.1.Let(V1/2A−1/2)∗=A−1/2V1/2denote the adjoint operator ofV1/2A−1/2.By duality,for givenp,q∈(1,2]with 1/p−1/q=α/n,it suffices to prove[b,A−1/2V1/2]is bounded fromLq′(Rn)toLp′(Rn).To obtain the conclusion,it suffices to prove that there exists a constantCsuch that for all where forr∈[2,n/α)and any suitable functionf, In fact,assume that(2.1)holds.Forb∈Lipα(Rn)and eachN∈N,definebN:=min{N,|b|}sgn(b).Then we conclude thatbN∈L∞(Rn)and kbNkLipα(Rn)≤CkbkLipα(Rn),whereCis a constant.Moreover,it has been proved in Theorem1.1 of[14]thatV1/2A−1/2is bounded onLp(Rn)for all 1 Recall thatM2,αis bounded fromLs(Rn)toLt(Rn)withs∈(2,n/α)and 1/s−1/t=α/n,see Chanillo[2].By this fact together with 1/q′−1/p′=α/n,Lemma 2.1 and(2.1),we have that for all A standard argument together with the Fatou lemma then implies that for all and which imply Theorem 1.1. Now,we prove(2.1)is valid.For anyf∈Lq′(Rn),andx∈Rn,choose a ballB:=B(xB,rB)={y∈Rn:|xB−y| and for any functionfand ballB,where Therefore, Firstly,we get For I,by the Hlder inequality and(2.3),we have For II,using the Hlder inequality again and theL2(Rn)-boundedness ofT,if follows that To estimate III,it follows from[5]that the kernelpt(y,z)ofe−tAsatisfies that for allt>0 and almost ally,z∈Rn, Letg:=(b−bB)Tf.By(2.4),the formula equation ofe−|x|≤C|x|−Nand the conclusion of I,for anyy∈B, whereN>n/2.So for III,it is easy for us to get For IV,for all locally integrable functionsfandx∈Rn,letM(f)(x)be the Hardy-Little wood maximal function as follow: By(2.4),the conclusion of II,the Hlder in equality and theL2(Rn)-boundedness ofTandM,we conclude that In order to estimate the term V,we need the following Proposition 2.1 and Lemma 2.2. Proposition 2.1(cf.Proposition 3.1 in[5]).Fixs>0.LetA=−(∇−)·(∇−)+Vbe the magnetic Schrdinger operator.Then for anym∈N,there exist positive constantsCandcsuch that for alls>0 andy∈Rn. Lemma 2.2.For a real vector potential~a=(a1,···,an)and an electric potential V,we as-sume that ak∈Then the composite operator(I−e−tA)A−1/2V1/2,t>0,which is the adjoint operator of V1/2A−1/2(I−e−tA),has an associated kernel(y,z)which satisfies Proofof Lemma 2.2.Firstly,we need to compute the(y,z)of(I−e−tA)A−1/2V1/2.Observe that then we have Therefore, By Minkowski’s inequality,we have Together with Proposition 2.1,this gives We first estimate the term I1.Note thatχs>t≡ 0 fors Consider the term II1.Oberve that,fors>t,thenχs>t=1.A direct calculation shows that Substituting the above into the term II1,we obtain Because thatt Therefore, Finally,we estimate the term II1,2.Sinces>2t,we have thatHence, Combining the estimates of I1,II1,1,II1,2we obtain(2.5).Hence,the proof of(2.5)is complete.Now,we will start the proof of Theorem 1.1. Proofof Theorem 1.1.Let us consider the term V.We have that So the kernelof the operatorsatisfies the following estimate whereCis a constant independent oftandy. Finally,from the fact that|y−z|≥rBfor anyy∈B,z/∈2B,the conclusion of(2.3),Lemma 2.2 and the Hlder inequality,the term V is dominated as follows, Combining the estimates from I to V,we see that(2.1)holds,which completes the proof of Theorem 1.1. ? Acknowledgements This work is supported by the National Natural Science Foundation of China(No.11671031 and No.11471018),the Fundamental Research Funds for the Central Universities(No.FRF-BR-17-004B),Program for New Century Excellent Talents in University,Beijing Municipal Science and Technology Project(No.Z17111000220000). References [1]B.Bongioanni,E.Harboure and O.Salinas,Commutators of Riesz transforms related to Schrdinger operators,J.Fourier Anal.Appl.,17(2011),115–134. [2]S.Chanillo,A note on commutators,Indiana Univ.Math.J.,31(1982),7–16. [3]R.R.Coifman,R.Rochberg and G.Weiss,Factorzation theorems for Hardy spaces in seval variables,Ann.Math.,103(1976),611–635. [4]S.Janson,Mean oscillation and commutators of singular integrals operators,Ark.Mat.,16(1978),263–270. [5]X.T.Duong and L.Yan,Commutators of Riesz transforms of magnetic Schrdinger operators,Manuscripta Math.,127(2008),219–234. [6]Z.H.Guo,P.T.Li and L.Z.Peng,Lpboundedness of commutators of Riesz transform associated to Schrdinger operator,J.Math.Anal.Appl.,341(2008),421–432. [7]P.T.Li and L.Z.Peng,Endpoint estimates for commutators of Riesz transform associated with Schrdinger operators,Bull.Australian Math.Soc.,82(2010),367–389. [8]Y.Liu,Commutators of BMO functions and degenerate Schrdinger operators with certain nonnegative potentials,Monatsh.Math.,165(2012),41–56. [9]Y.Liu,J.Z.Huang and J.F.Dong,Commutators of Calder´on-Zygmund operators related to admissible functions on spaces of homogeneous type and applications to Schrdinger operators,Sci.China.Math.,56(2013),1895–1913. [10]Y.Liu,L.J.Wang and J.F.Dong,Commutators of higher order Riesz transform associated with Schrdinger operators,J.Function Spaces Appl.,(2013),Article ID 842375,15 pages. [11]Y.Liu and J.L.Sheng,Some estimates for commutators of Riesz transforms associated with Schrdinger operators,J.Math.Anal.Appl.,419(2014),298–328. [12]S.Z.Lu,Q.Wu and D.C.Yang,Boundedness of commutators on Hardytype spaces,Science in China(Series A),45(2002),984–997. [13]J.M.Martell,Sharp maximal functions associated with approximations of the identity in spaces of homogeneous type and applications,Studia Math.,161(2004),113–145. [14]X.T.Duong,E.M.Ouhabaz and L.X.Yan,Endpoint estimates for Riesz transforms of magnetic Schrdinger operators,Ark.Mat.,44(2006),261–275. [15]Z.W.Shen,Estimates inLpfor magnetic Schrdinger operators,Indiana Univ.Math.J.,3(1996),817–841. [16]D.Y.Yang,Commutators of Riesz transforms with Lipschitz functions related to Schrdinger operators,Math.Inequal.Appl.,19(2016),173–184.
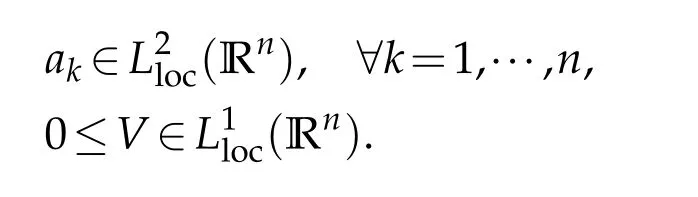
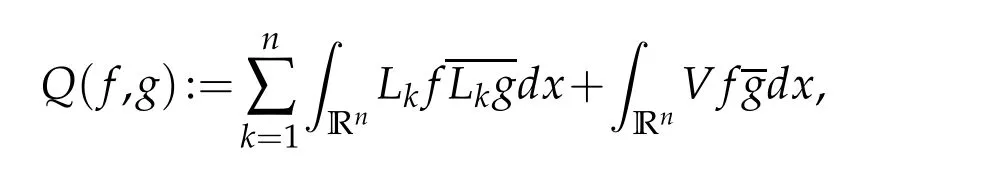
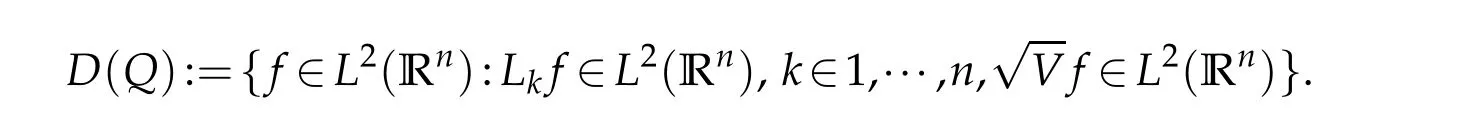
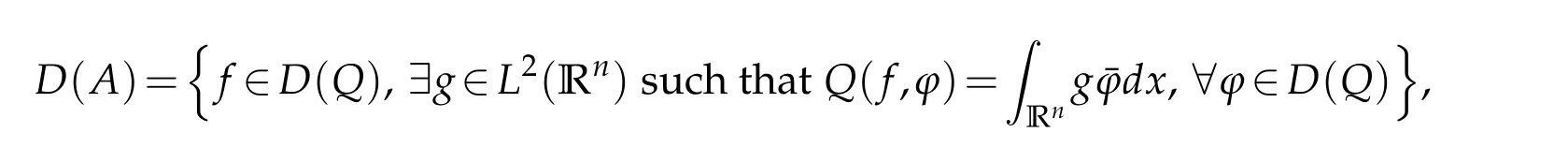
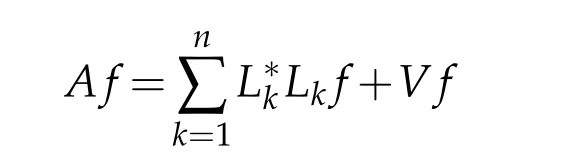
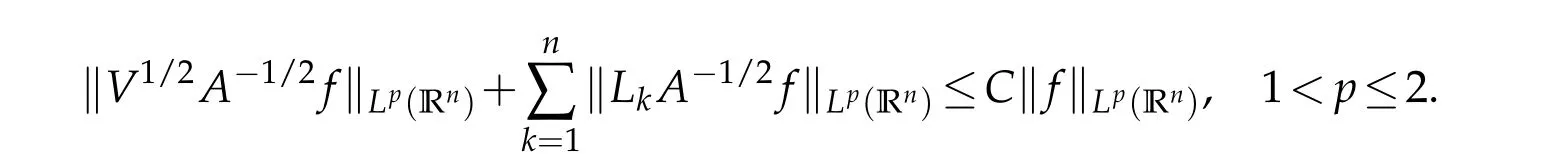
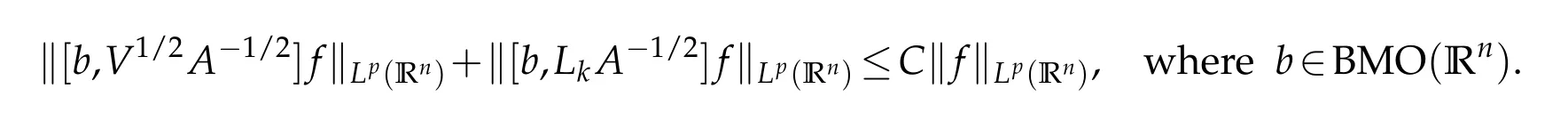
2 Proof of Theorem 1.1


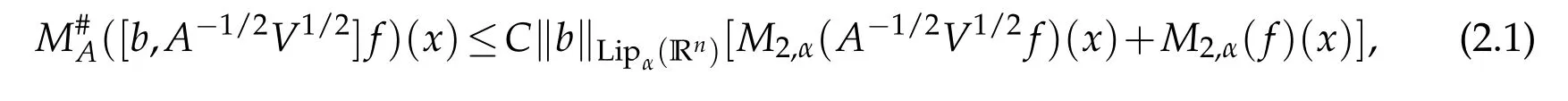

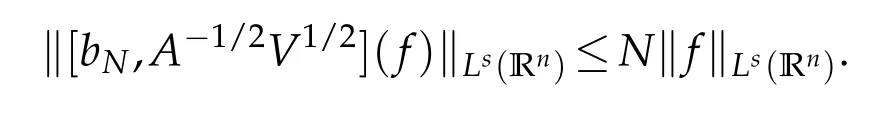
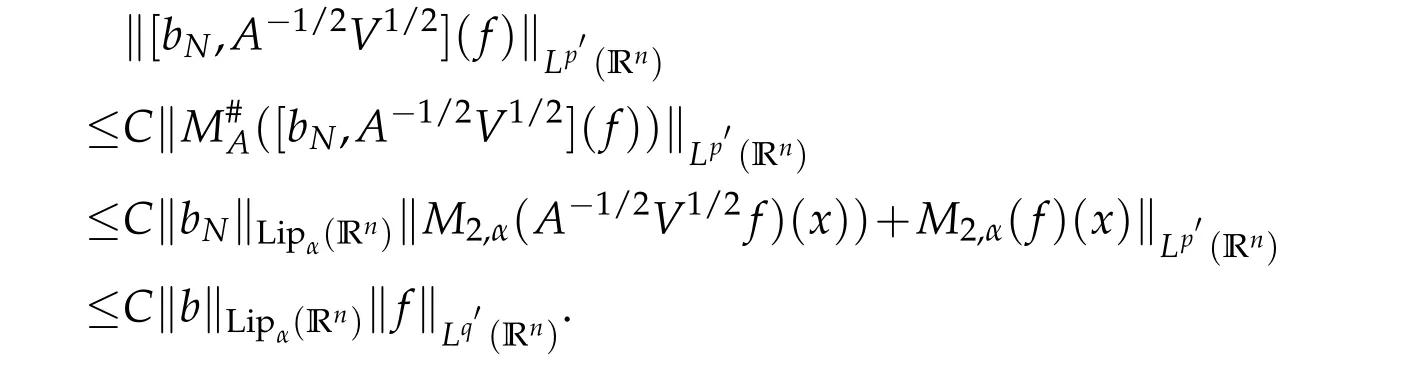
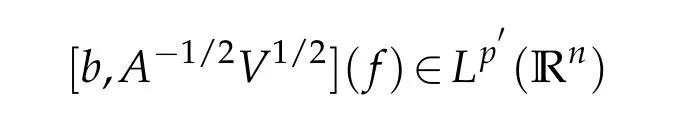
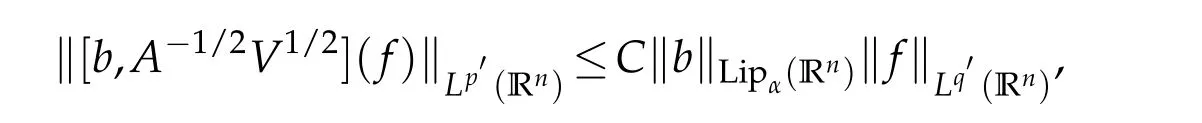
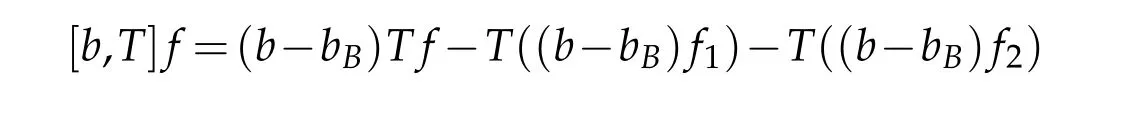
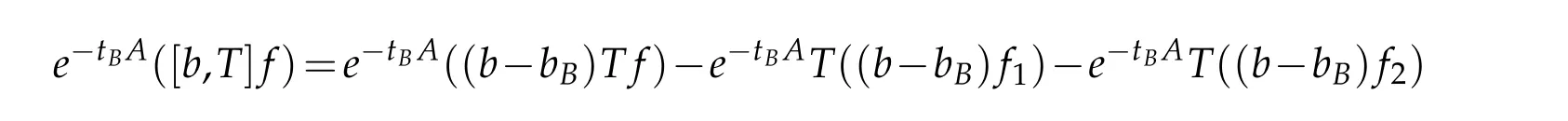

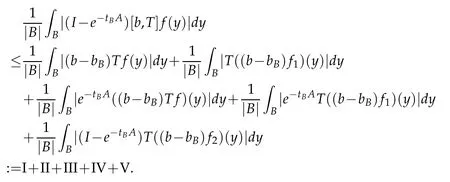
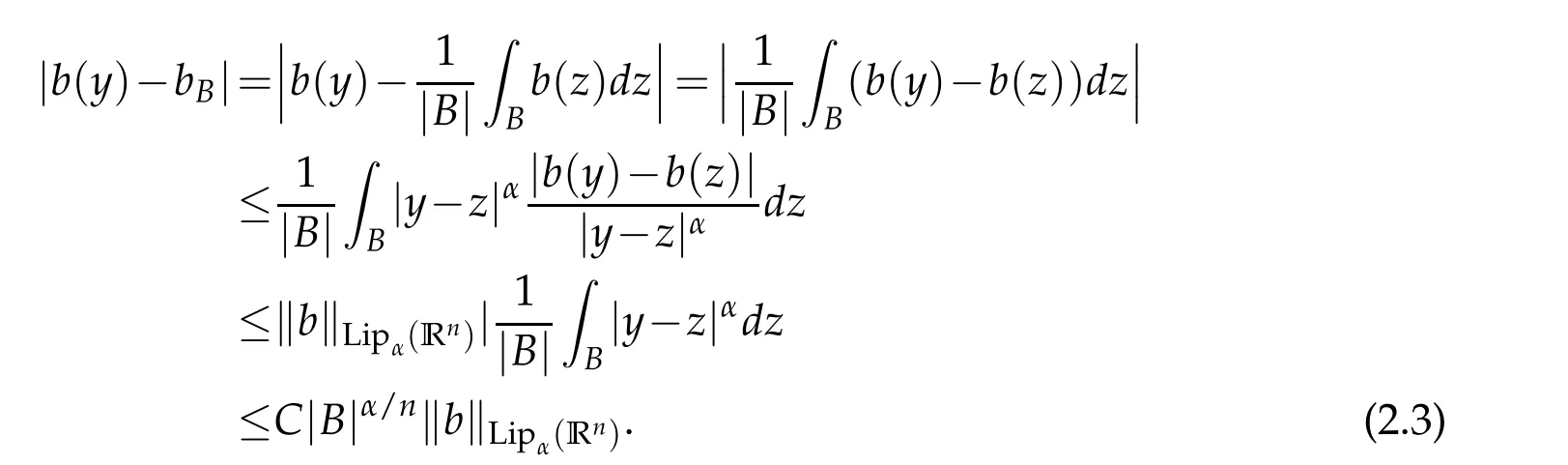
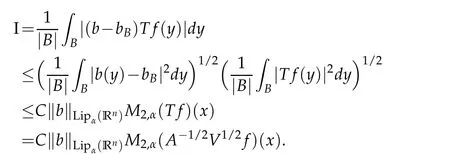
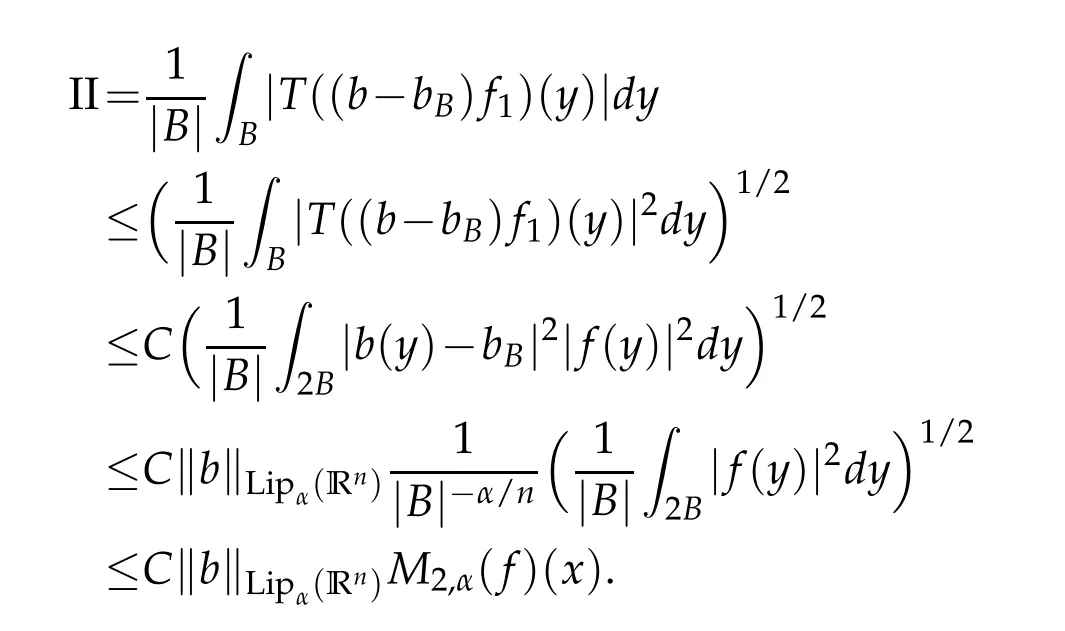
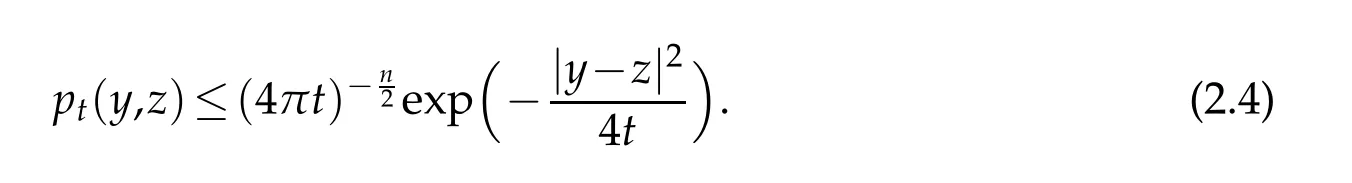

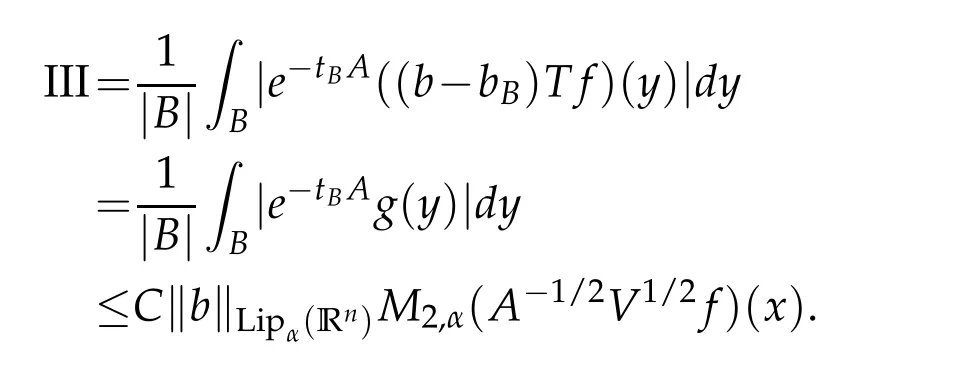
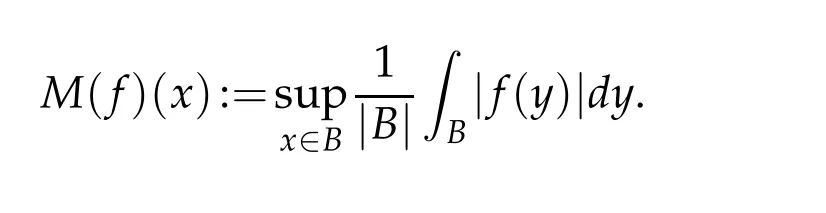
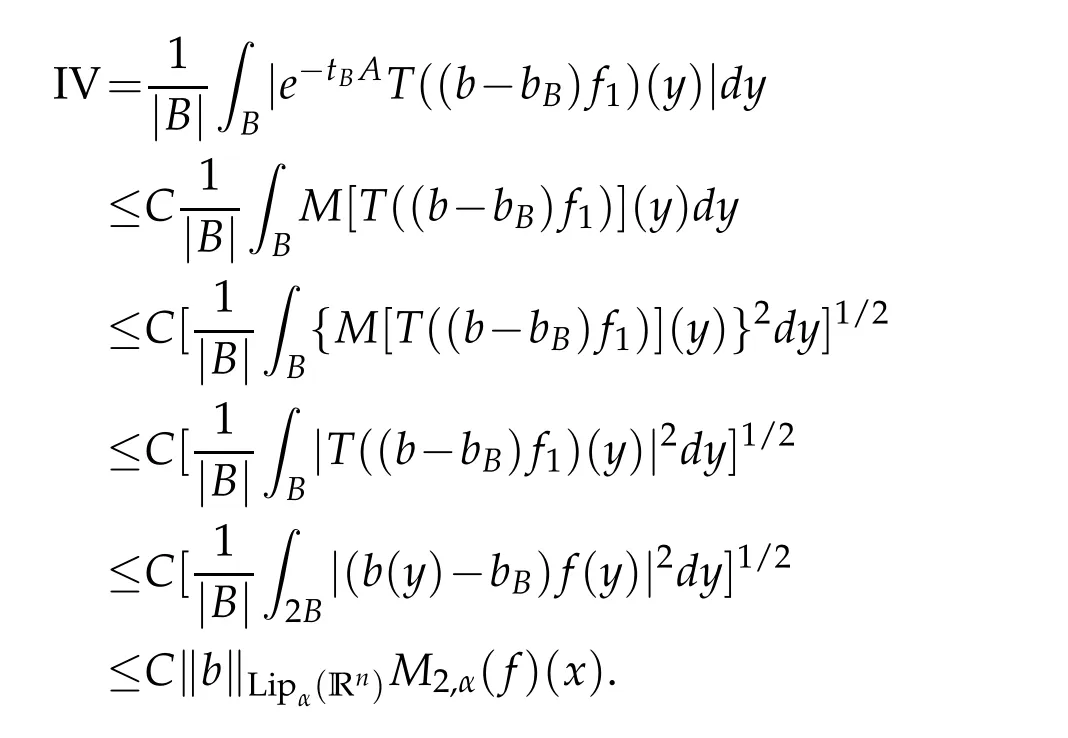


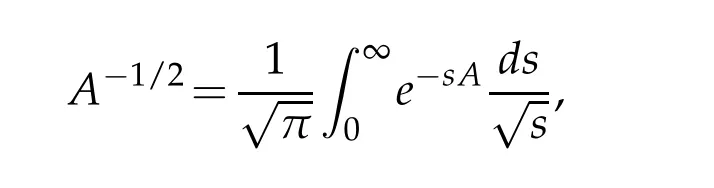
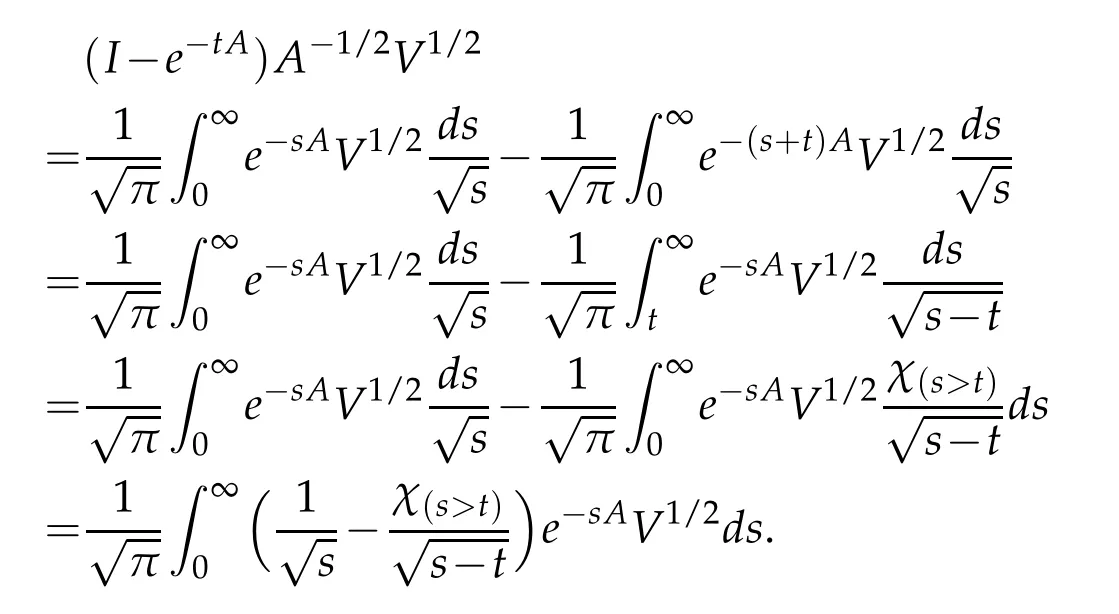

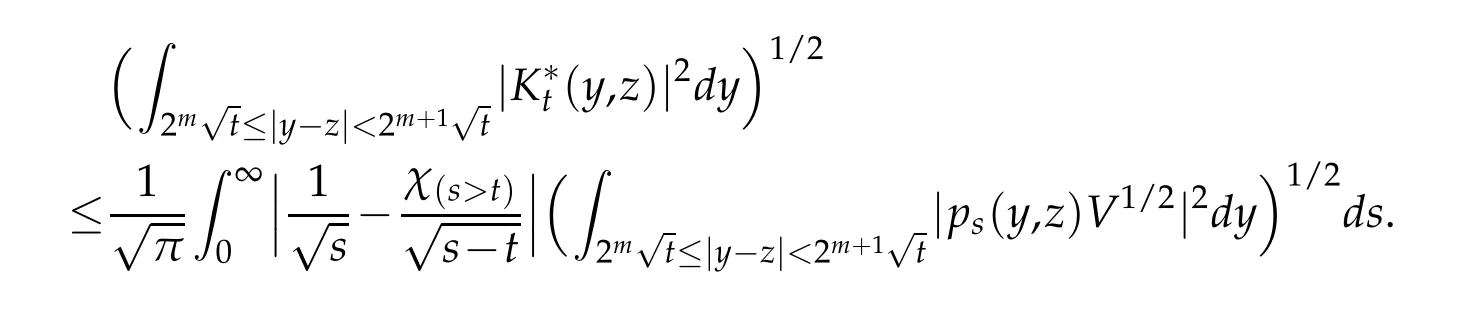
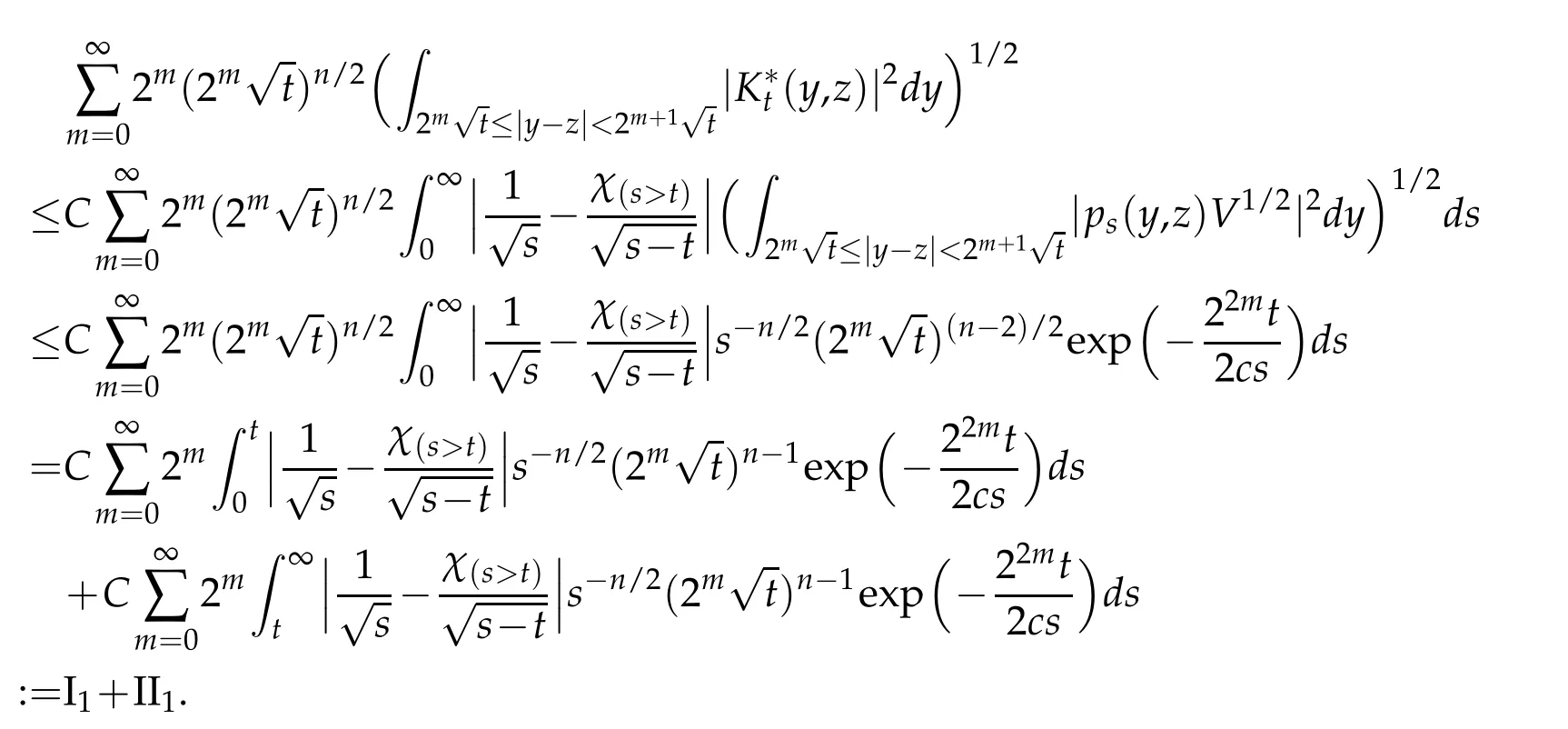
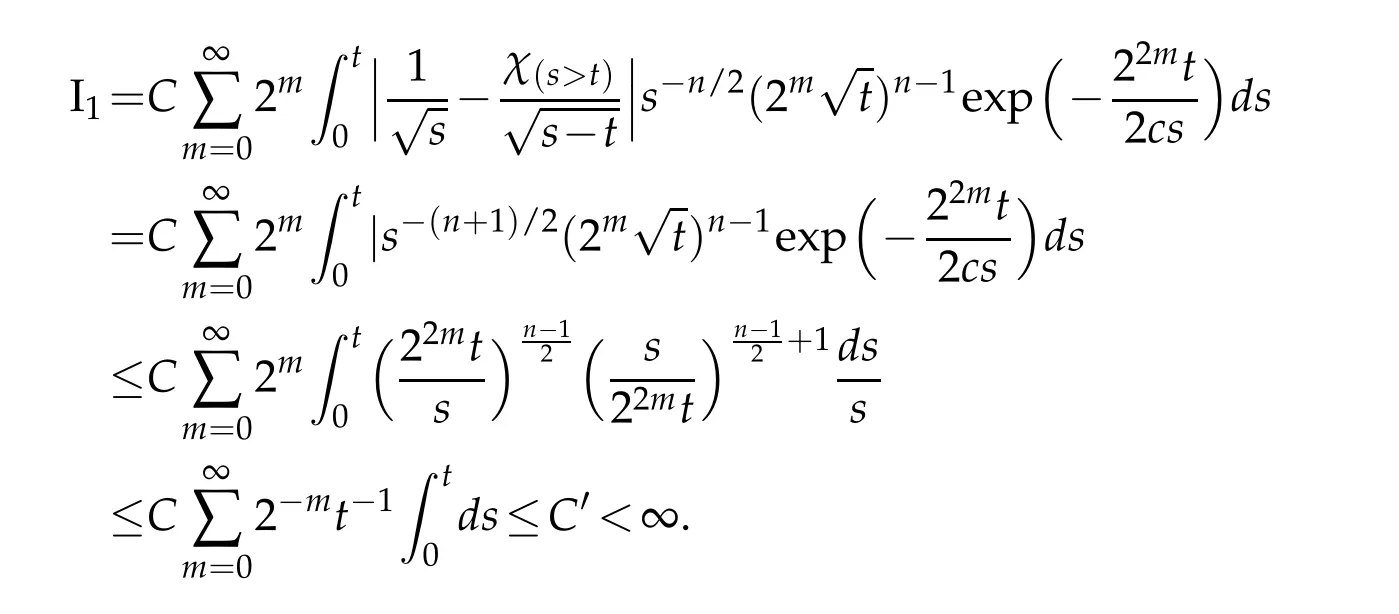
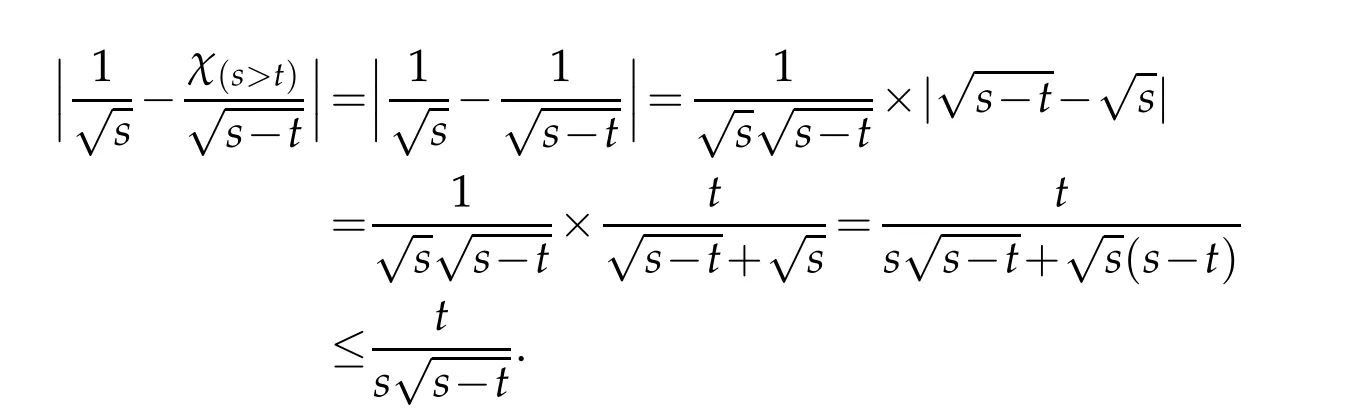

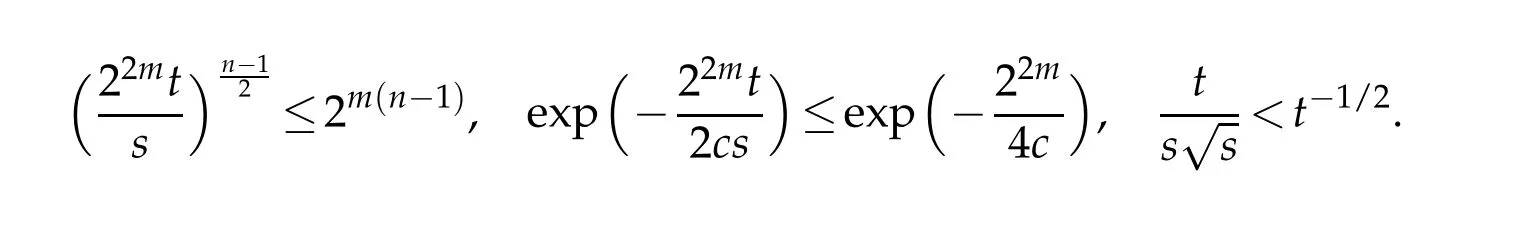
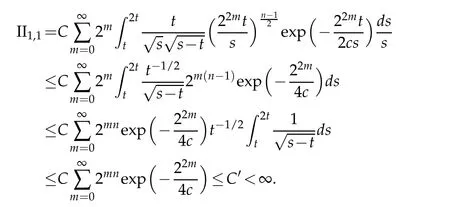
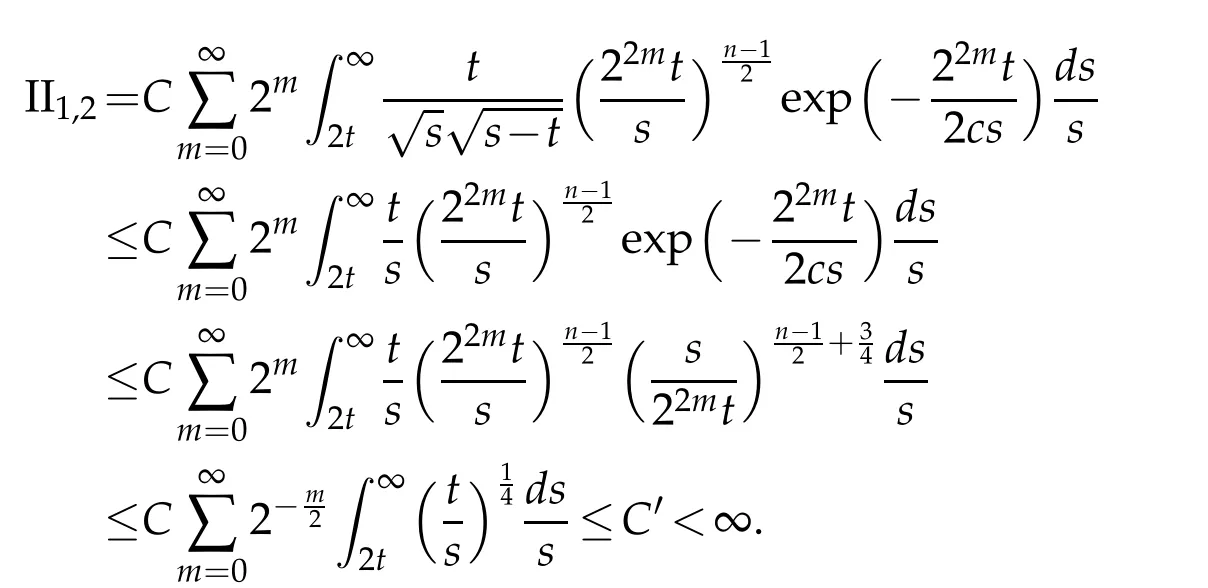
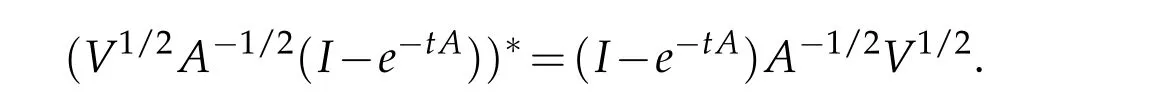
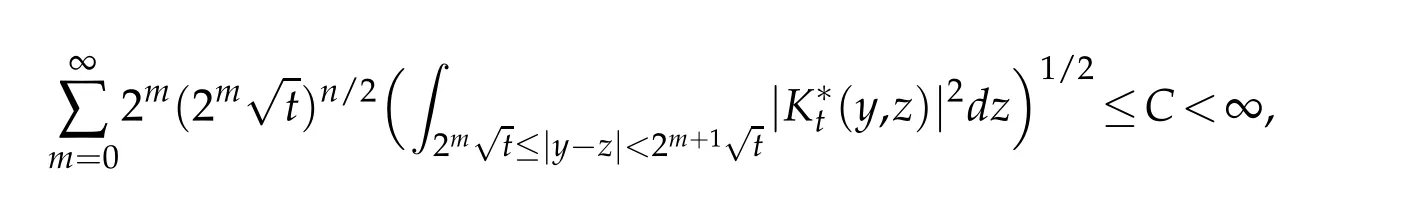
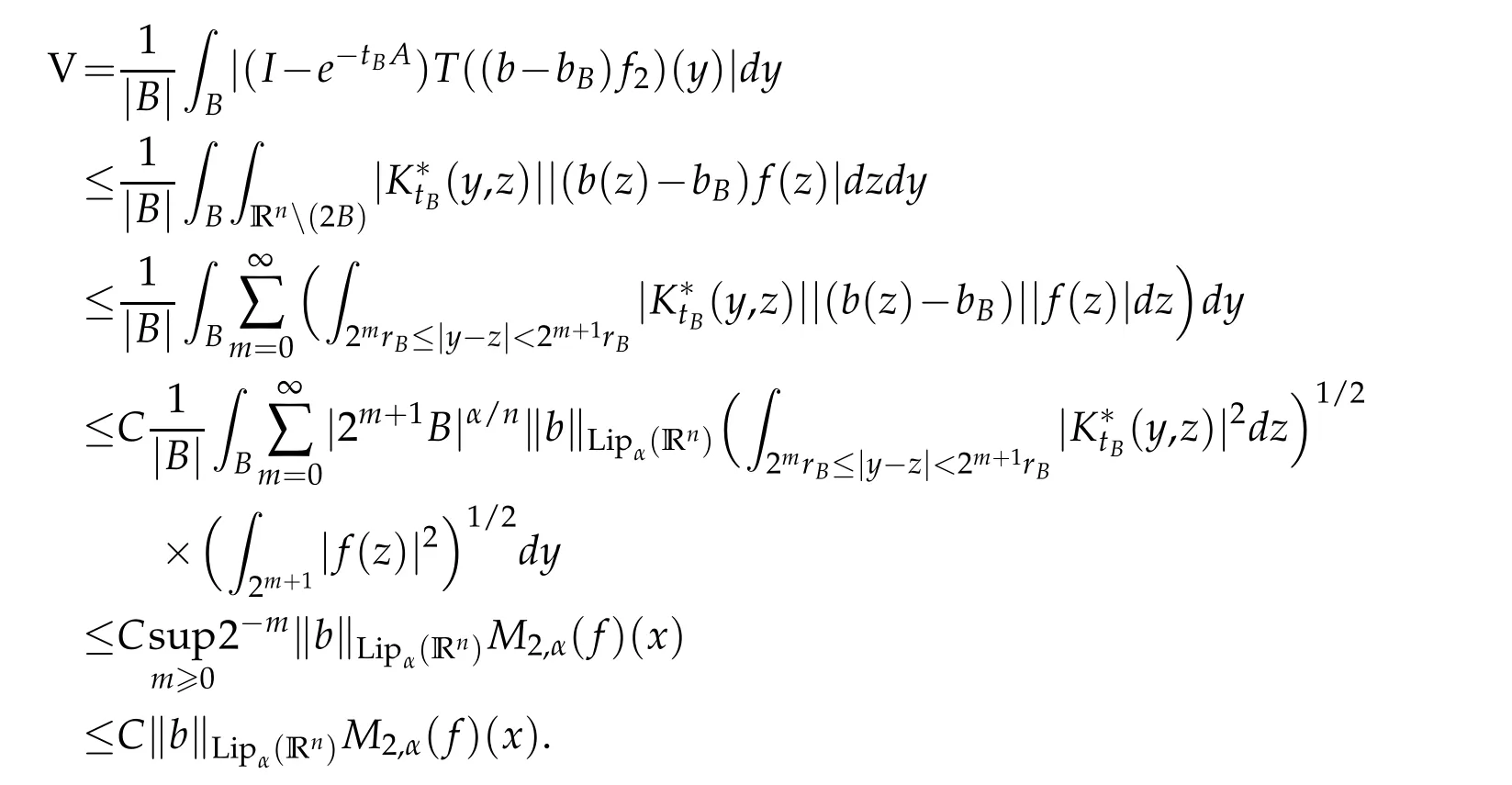
杂志排行
Analysis in Theory and Applications的其它文章
- On Weighted Lp−Approximation by Weighted Bernstein-Durrmeyer Operators
- A Struwe Type Decomposition Result for a Singular Elliptic Equation on Compact Riemannian Manifolds
- On an Axiomatic about Functional Means
- Some Generalized q-Bessel Type Wavelets and Associated Transforms
- Approximation for Certain Stancu Type Summation Integral Operator
- On Quasi-Chebyshevity Subsets of Unital Banach Algebras
