A Struwe Type Decomposition Result for a Singular Elliptic Equation on Compact Riemannian Manifolds
2018-05-24YoussefMalikiandFatimaZohraTerki
Youssef Malikiand Fatima Zohra Terki
1Department of Mathematics,University Aboubekr Belkaid of Tlemcen,Tlemcen,Algeria
2Higher School in Business and Management,Tlemcen,Algeria
1 Introduction
Let(M,g)be an(n≥3)−dimensional Riemannian manifold.In this paper,we are interested in studying on(M,g)the asymptotic behaviour of a sequence of solutionsuα,whenα→∞,of the following singular elliptic equation:

whereandfare functions onM,pis a fixed point ofMandρp(x)=distg(p,x)is the distance function onMbased atp(see Definition 2.2).
Certainly,if the singular termis replaced bythen equationEαbecomes the prescribed scalar curvature equation which is very known in the literature.Whenfis constant and the functionρpis of power 0<γ<2,Eq.(Eα)can be seen as a case of equations that arise in the study of conformal deformation to constant scalar curvature of metrics which are smooth only in some ballBp(δ)(see[5]).
Equations of type(Eα)have been the subject of interest especially on the Euclidean spaceIRn.LetD1,2(IRn)be the Sobolev space defined as the completion of(IRn),the space of smooth functions with compact support inIRn,with respect to the norm
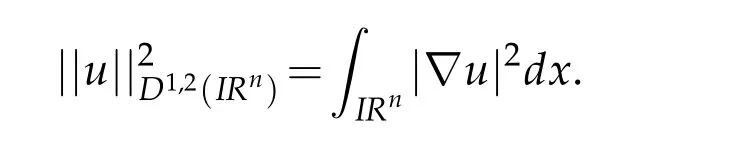
A famous result has been obtained in[8]and it consists of the classification of positive solutionsu∈D1,2(IRn)of the equation

whereinto the family of functions
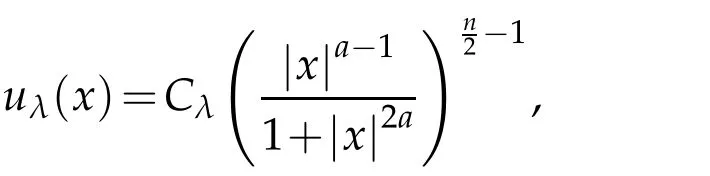
whereCλis some constant and
In terms of decomposition of Palais-Smale sequences of the functional energy,this family of solutions was employed in[6]to construct singular bubbles,
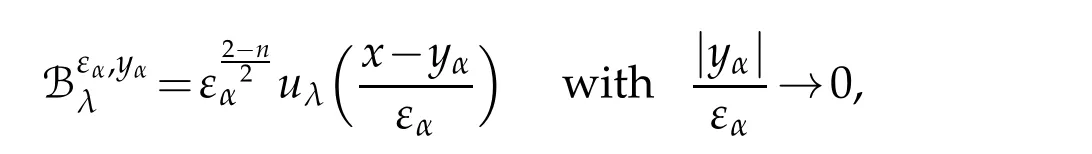
which,together with the classical bubbles caused by the existence of critical exponent
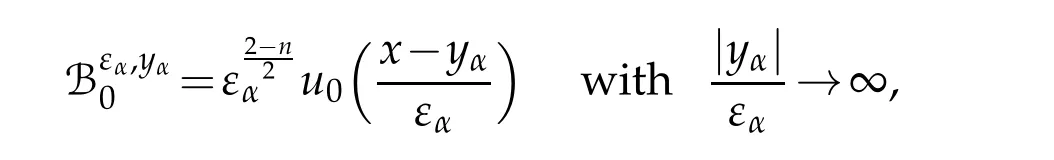
whereu0being the solution of the non perturbed equation ∆u=,give a whole picture of the decomposition of the Palaise-Smale sequences.This decomposition result has been proved in[6]and was the key component for the obtention of interesting existence results for Eq.(E)with a functionKget involved in the nonlinear term.Similar decomposition result has been obtained in[1]for Eq.(E)with small perturbation,the authors described asymptotically the associated Palais-Smale sequences of bounded energy.
The compactness result obtained in this paper can be seen as an extension to Riemannian context of those obtained in[6]and[1]in the Euclidean context,the difficulties when working in the Riemannian setting reside mainly in the construction of bubbles.
Historically,a famous compactness result for elliptic value problems on domains of Rnhas been obtained by M.Struwe in[7].Struwe’s result has been extended later by O.Druet et al.in[2]to elliptic equations on Riemannian manifolds in the form
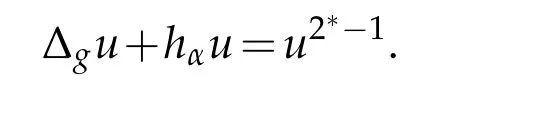
Many results have been obtained by the authors describing the asymptotic behaviour of Palais-Smale sequences.The authors gave a detailed construction of bubbles by means of a re-scaling process via the exponential map at some points,supposed to be the centers of bubbles.The author in[3]followed the same procedure to prove a decomposition result on compact Riemannian manifolds for a Sobolev-Poincarequation.
In this paper,we follow closely the work in[2]to prove a decomposition theorem for Eq.(Eα).More explicitly,after determining conditions under which solutions of(Eα)exist,we prove as in[6]and[1]that,under some conditions on the sequencehαand the functionf,a sequence of solutions of(Eα)of arbitrarily bounded energy decomposes into the sum of a solution of the the limiting equation
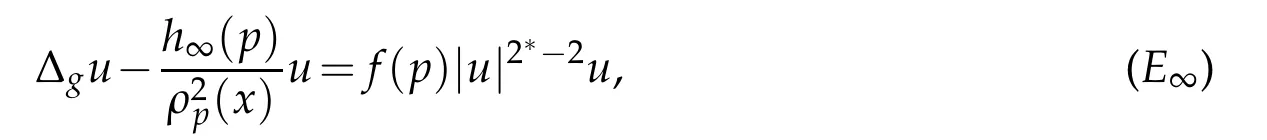
whereh∞is the uniform limit ofhα,and two kinds of bubbles,namely the classical and the singular ones due to the presence respectively of the critical exponent and the singular term.
2 Notations and preliminaries
In this section,we introduce some notations and materials necessary in our study.Let(M)be the Sobolev space consisting of the completion of C∞(M)with respect to the norm
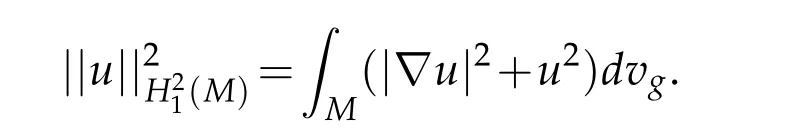
Mbeing compact,(M)is then embedded inLq(M)compactly forq<2∗and continuously forq=2∗.
LetK(n,2)denote the best constant in Sobolev inequality that asserts that there exists a constantB>0 such that for anyu∈(M),
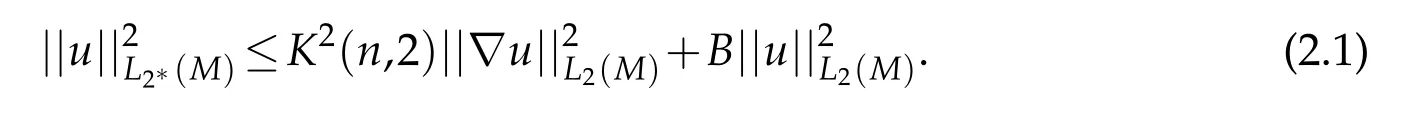
Throughout the paper,we will denote byB(a,r)a ball of centeraand radiusr>0,the pointawill be specified either inMor inIRn,andB(r)is a ball inIRnof center 0 and radiusr>0.
Denote byδgthe injectivity radius ofM.Letp∈Mbe a fixed point,as in[5]we define the functionρponMby
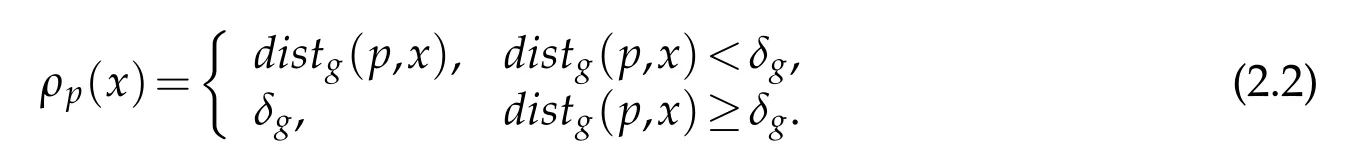
Forq≥1,we denote byLq(M,)the space of functionsusuch that
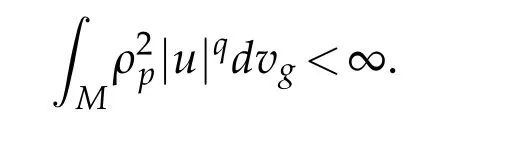
This space is endowed with norm
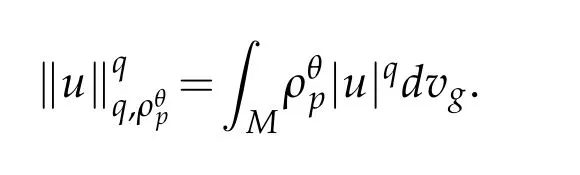
In[5],the following Hardy inequality has been proven on any compact manifoldM,for everyε>0 there exists a positive constantA(ε)such that for anyu∈(M),
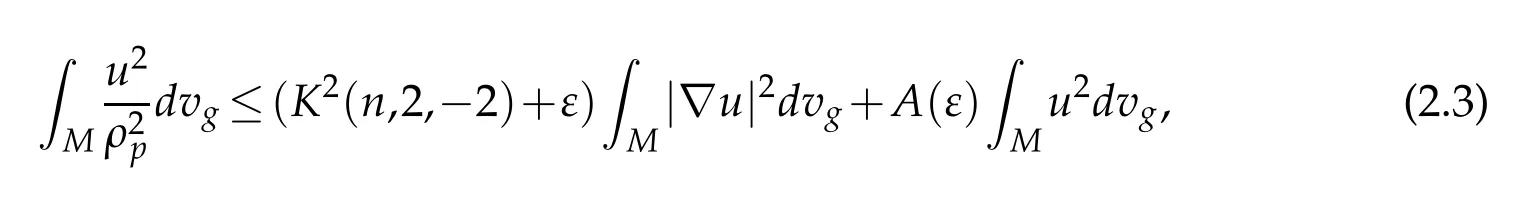
withK(n,2,−2)being the best constant in the Euclidean Hardy inequality
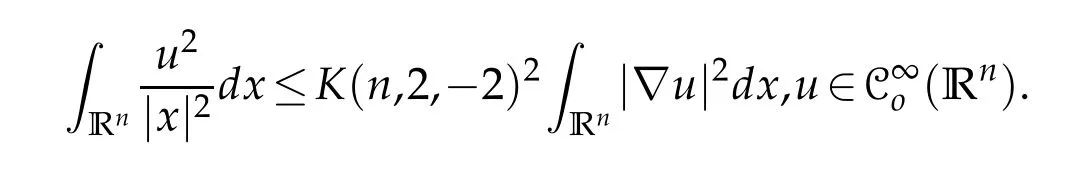
Ifuis supported in a ballB(p,δ),0<2δ<δg,then
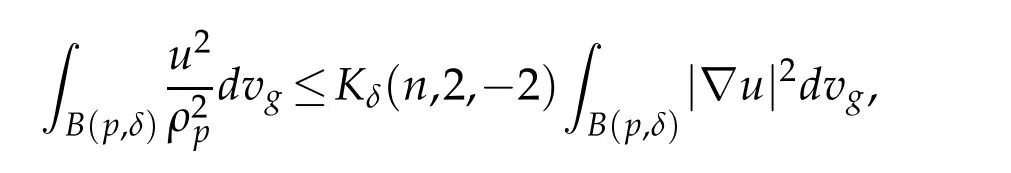
withKδ(n,2,−2)goes toK(n,2,−2)whenδgoes to 0.
Concerning the existence of solutions of Eqs.(Eα),the author in[5]proved through the classical variational techniques an existence result withfa constant function.Following closely the strategy in[5],we obtain the existence of a weak solutionuαof the Eq.(Eα).This existence result is formulated in the following theorem and due to the very familiarity of the techniques used,in order to avoid heaviness in the paper,we omit the proof(for a good presentation of these techniques,see for example[4]).Foru∈(M),set
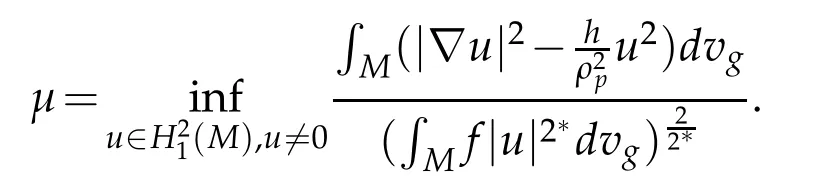
The following theorem ensures conditions under which a weak solutionuαof(Eα)exists.
Theorem 2.1.Let(M,g)be a compact n(n≥3)−dimensional Riemannian manifold and f,hα(α∈[0,∞])be continuous functions on M.Under the following conditions:
Eq.(Eα)admits a nontrivial weak solution uα
3 Decomposition theorem
LetJαbe the functional defined on(M)by
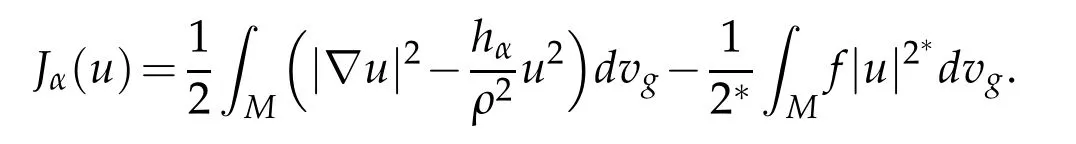
Traditionally,we define a Palais-Smale sequencevαofJαat a levelβas to be the sequence that satisfiesJα(vα)→βandDJα(vα)ϕ→0,∀ϕ∈(M).
Define the following limiting functionals
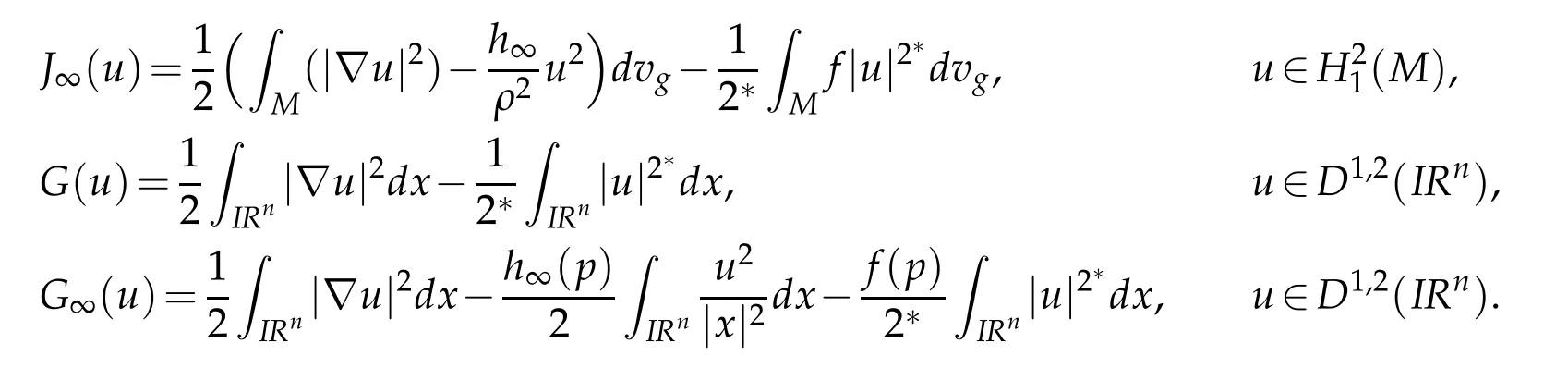
Forα∈[0,∞],lethαbe a sequence of continuous functions onMsuch that

Now,we state our main result
Theorem 3.1.Let(M,g)be a compact Riemannian manifold with dim(M)=n≥3,hαbe a sequence of continuous functions on M satisfying(H),f be a positive continuous function onM that satisfies with hαthe conditions of Theorem 2.1.Let uαbe a sequence of weak solutions of(Eα)such thatdvg≤C,∀α>0.Then,there exist k∈IN,sequencesl∈IN sequencesconverging sequences→6=p in M,a solution uoof(E∞),solutions vi∈D1,2(IRn)of(3.9)and nontrivial solutions νj∈D1,2(IRn)of(3.14)such that up to a subsequence
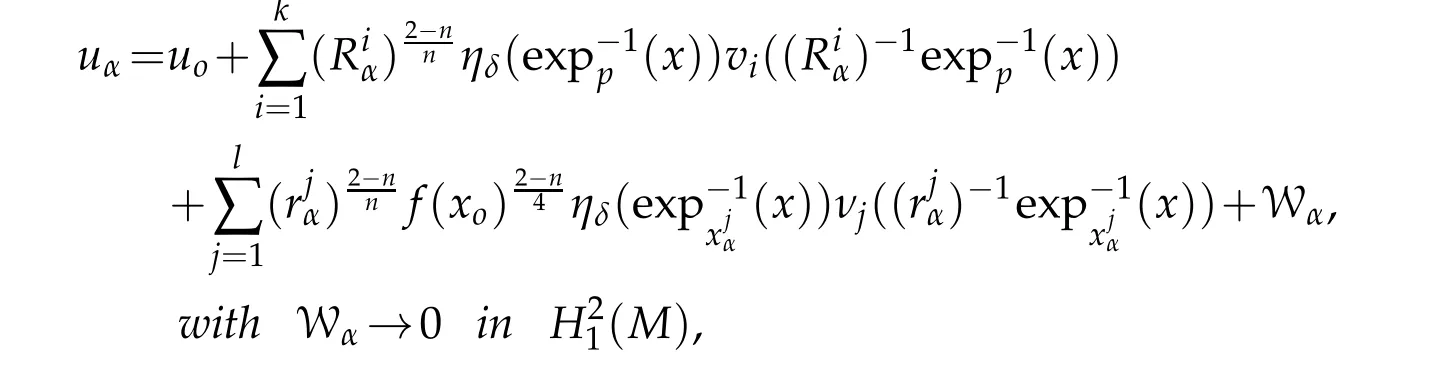
and
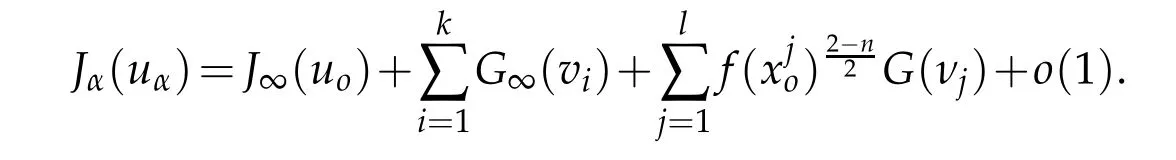
In order to prove this theorem,we prove some useful lemmas.In all what follows,hαis supposed to satisfy conditions(H).
Lemma 3.1.Let uαbe a Palais-Smale sequence for Jαat level β that converges to a function u weakly in(M)and L2(M,),strongly in Lq(M),1≤q<2∗and almost everywhere in M.Then,the sequence vα=uα−u is sequence of Palais-Smale for Jαand
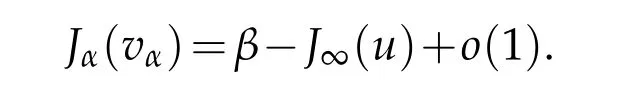
Proof.First,in view of the fact thatuαis a Palais-Smale sequence forJα,uαis bounded in(M).In fact,DJα(uα)uα=o(||u||H21(M))implies that
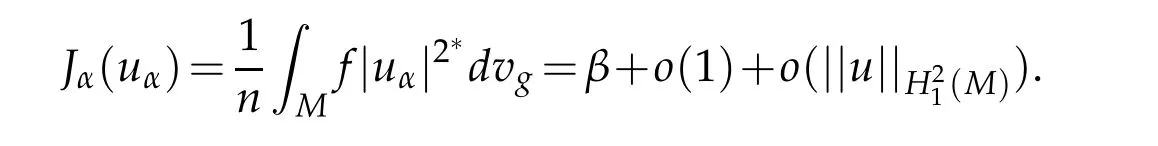
Sincef>0,this implies in turn thatuαis bounded inL2∗(M)and then inL2(M).Furthermore,we have
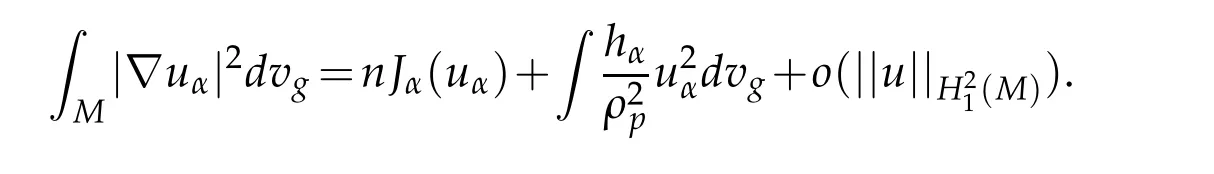
By continuity ofhαonp,we have that for allǫ>0 there existsδ>0 such that
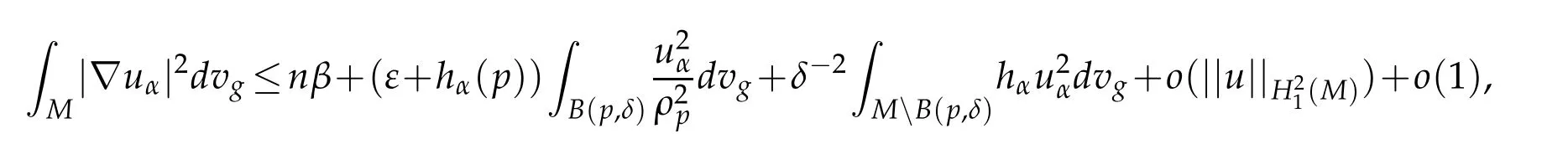
then,by applying Hardy inequality(2.3)that for everyε>0 small there exists a constantA(ε)such that
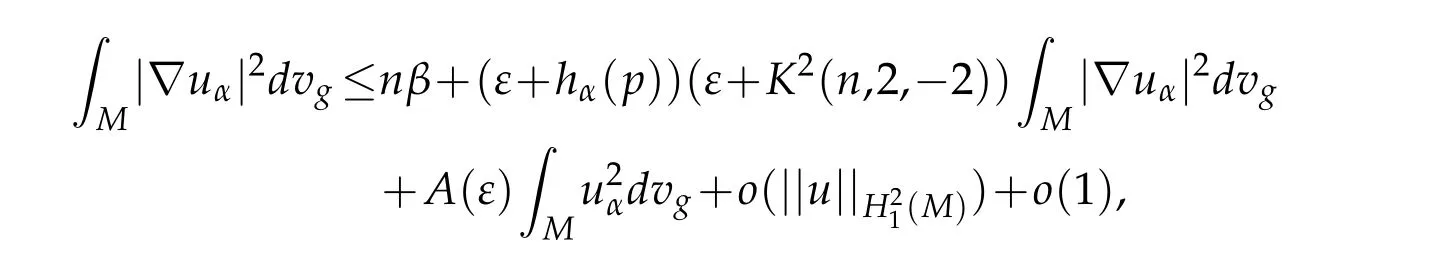
since0we can findε>0 small such that1−(ε+hα(p))(ε+K2(n,2,−2))>0,which implies thatis bounded.Thus,uαbounded in(M).
Now,for two functionsϕ,φ∈(M),Hlder and Hardy inequalities give
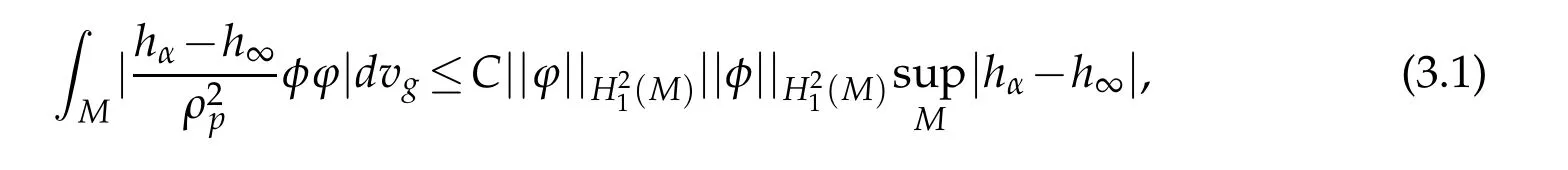
writing
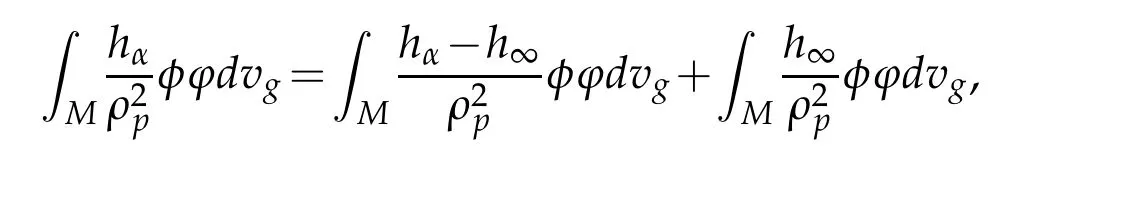
we get by the assumption made on the sequencehαthat
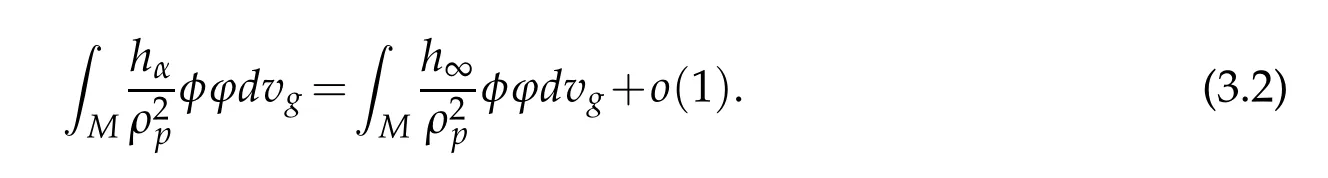
Then,since the sequenceuαis bounded in(M),by takingφ=uα,we get from(3.1)together with the weak convergence ofuαtouinL2(M,ρ−2)that
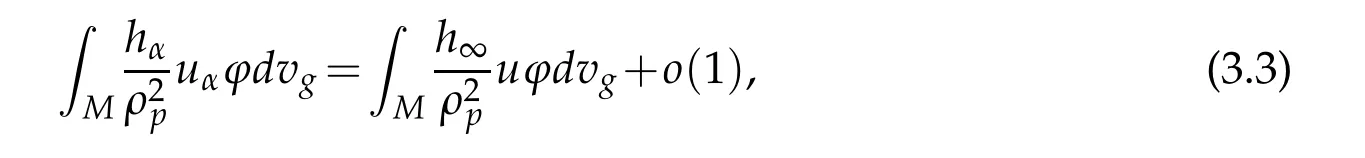
thus,applying the last identity toϕ=u,we get by the weak convergence inH21(M)that
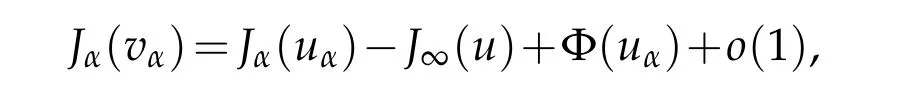
with
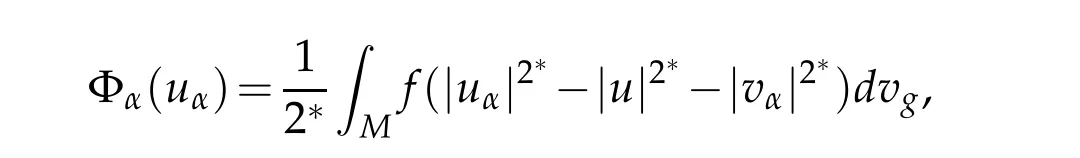
which by the Brezis-Lieb convergence Lemma equals too(1),hence we obtain

Moreover,forϕ∈(M),by takingφ=uin(3.2),we can write
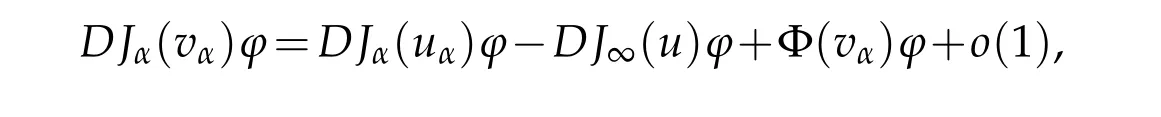
with
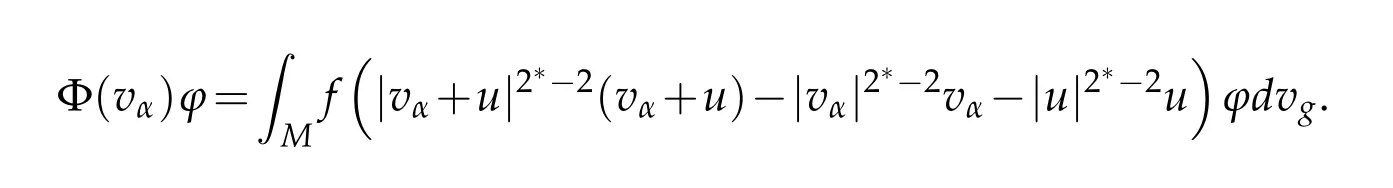
Knowing that there exists a positive constantCindependent ofαsuch that
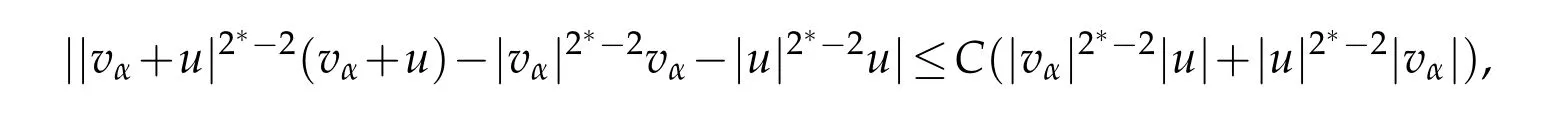
we get,after applying Hlder inequality,that there exists a positive constantCsuch that
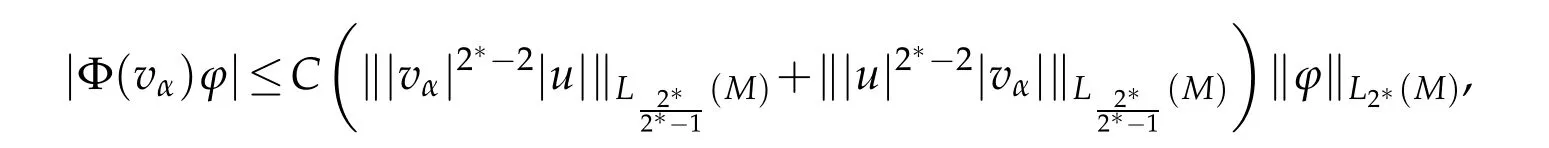
which gives thatsince bothare smaller than 2∗and the inclusion ofis compact forq<2∗.
On the other hand,since the sequenceis bounded inand converges almost everywhere tou2∗−2u,we get thatconverges weakly intou2∗−2u.This,together with the weak convergence inM)ofuαtouand relation(3.3),imply thatDJ∞(u)ϕ=0,∀ϕ∈(M).Hence,DJα(vα)ϕ→0,∀ϕ∈(M).
Lemma 3.2.Let vαbe a Palais-Smale sequence of Jαat level βthat converges weakly to0in(M).If

then vαconverges strongly to0in(M).
Proof.Ifvαis a Palais-Smale sequence ofJαat levelβthat converges to 0 weakly in(M),thenand

This implies thatβ≥0.Hence,on the one hand,by Hardy inequality(2.3)we get as in Lemma 3.1,that for small enoughε>0,

and on the other hand,by Sobolev inequality(2.1),we also get
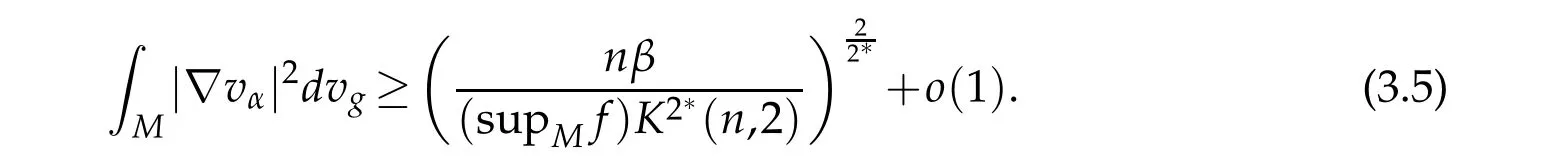
Now,suppose thatβ>0,then the above inequalities(3.4)and(3.5),forαbig enough,give
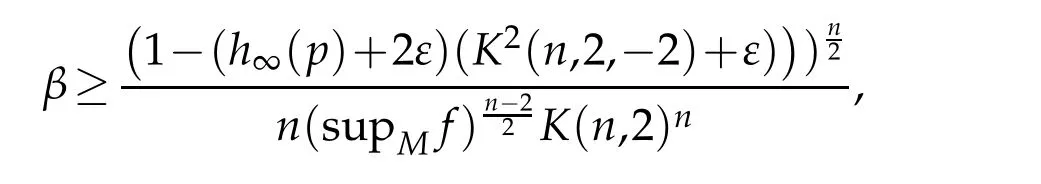
that is
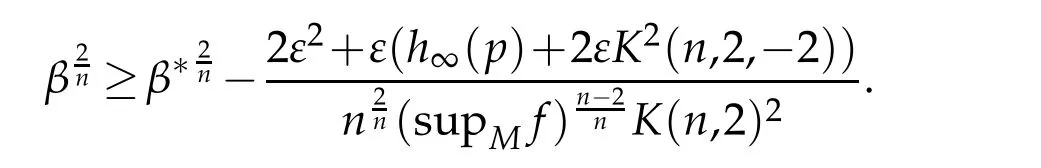
By assumptionβ∗>β,by takingε>0 small enough so that

we get a contradiction.Thusβ=0 and(3.4)assures that
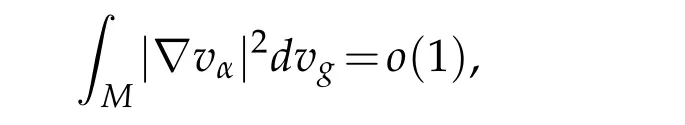
that isvα→0 strongly in
In the following,for a given positive constantR,define a cut-off functionηR∈(IRn)such thatηR(x)=1,x∈B(R)andηR(x)=0,x∈IRnB(2R),0≤ηR≤1 and|∇ηR|≤
Lemma 3.3.Let vαbe Palais-Smale sequence for Jαat level βthat weakly,but not strongly,converges to0in(M).Then,there exists a sequence of positive reals Rα→0such that,up to a subsequence,with
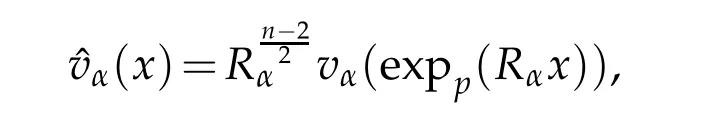
and(x)=ηδ(Rαx))(δ is some positive constant),converges weakly in D1,2(Rn)to a function v∈(Rn)such that,if v6=0,v is a weak solution of the Euclidean equation
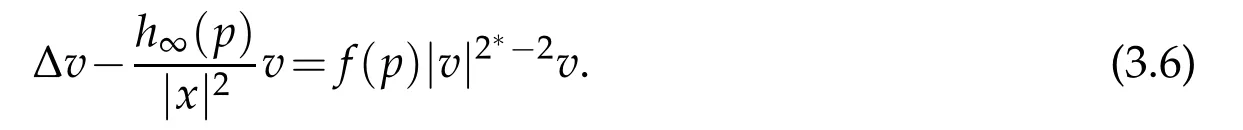
Proof.Since the Palais-Smale sequencevαofJαat levelβconverges weakly and not strongly in(M)to 0,we get by Lemma 3.2 thatβ≥β∗.Write
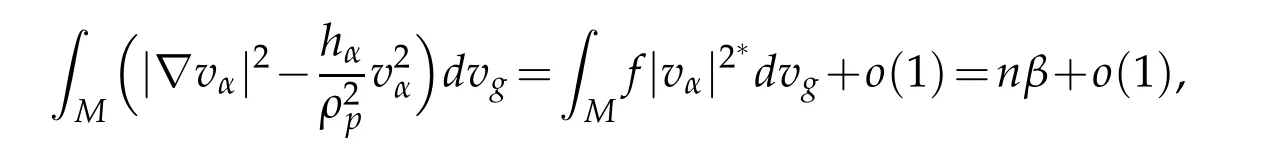
since,up to a subsequence,vαconverges strongly to 0 inL2(M),we get by Hardy inequality(2.3)that for allε>0 small
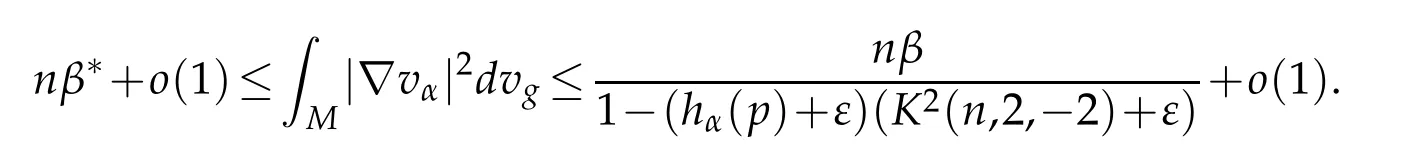
In other words,

for some positive constantsc1andc2.
Letγa small positive constant such that

Up to a subsequence,for eachα>0,we can find the smallest constantrα>0 such that
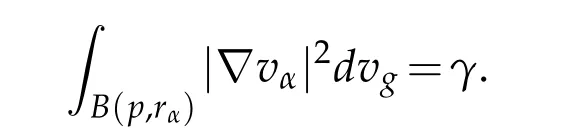
For a sequence of positive constantsRαanddefine
We follow the same arguments as in[2].Letr>0 be a constant andz∈Rnbe such thatthen we have

Let 0 for some positive constantCo.Also,forr∈(0,ro),takeRαbe such thatcorRα=rα,then we get and then Takeδsuch that 0<δ≤ minthere exists a positive constant such that,for allthe following inequalities hold Define a sequence of cut-off functionsby(x)=ηδ(Rαx).Then,it follows from(3.10),(3.11a)and(3.11b)that the sequence=is bounded inD1,2(IRn).Consequently,up to a subsequence,˜vαconverges weakly to some functionv∈D1,2(IRn). Suppose thatv6=0,sincevαconverges weakly to 0,it follows thatRα→0. Let us first prove thatvis a weak solution onD1,2(IRn)to(3.6).For this task,we letbe a function with compact support included in the ballB(δ).Forαlarge,define onMthe sequenceϕαas Then,we have When tendingαto∞,ˆgαtends smoothly to the Euclidean metric onIRn,then by passing to the limit whenα→ ∞ and sincevαis a Palais-Smale sequence ofJα,we get thatvis weak solution of(3.6). Lemma 3.4.Let v be the solution of(3.6)given by Lemma 3.3,then up to a subsequence, where0<δ<,is a Palais-Sequence for Jαat level β−G∞(v)that weakly converges to0in Proof.For 0<δ and put We begin proving thatwαconverges weakly to 0 in(M),it suffices to prove that Bαdoes.Take a functionϕ∈C∞(M),then we have then,for a positive constantC′such thatdvˆgα≤C′dx,it follows that Thus,when tendingα→∞,we ge that Bα→0 weakly inH21(M). Now,let us evaluateJα(wα).First,we have and of course Direct calculation gives It can be easily seen that the second term of right-hand side member of the above equality tends to 0 asα→∞.Furthermore,forR>0,a positive constant,we write with whereεRis a function inRsuch thatεR→0 asR→ ∞. Noting thatgoes locally inC1to the Euclidean metricξ,we get then Moreover,we have with Sincevαis bounded in(M),the quantitiesare bounded and hence the second term of the right-hand side member of(3.13)iso(1).Thus,by using the weak convergence ofˆηαˆvαtovinD1,2(IRn)that so that In the same fashion,forRa positive constant andαlarge,we write with then,by a direct calculations,we get Hence, Also,in similar way,sincevαis bounded inH21(M),after using Hlder and Hardy inequalities,we can easily have which yields so that in the end we obtain In similar way,we can prove that Finally,sinceRis arbitrary,when summing up we obtain It remains to prove thatandthen we have Knowing that we get that which gives that Next,forR>0 write note that whereεR→0 asR→∞.Since the sequence of metricstends locally inC1whenα→∞to the Euclidean metric,we obtain Moreover,for a givenR>0,we have forαlarge, On the one hand,we have and a straightforward computation shows that which implies that withεR→0 asR→∞. On the other hand,we have which leads to with so that In the same way,we can also have Summing up,we obtain and sincevis weak solution of(E∞),we get the desired result. Keeping the notations adapted above,we prove the following lemma Lemma 3.5.Let vαa Palais-Smale sequence for Jαat level β.Suppose that the sequence˜v=ˆηαˆvα of the above lemma converges weakly to0in D1,2(IRn).Then,there exist a sequence of positive numbers{τα},τα→0and a sequence of points xi∈M,xi→xo∈M{p}such that up to a subsequence,the sequence ηδ(ταx)να,with δ is some constant and converges weakly to a nontrivial weak solution ν of the Euclidean equation and the sequence is a Palais-Smale sequence for Jαat levelthat converges weakly to0in Proof.Suppose that the sequenceconverges weakly to 0 in D1,2(IRn).Take a functionϕ∈(B(Cor))and putAs in[6]and[1],by the strong convergence ofto 0 inwe have forαlarge Thus,forγchosen small enough,we get that for eacht,0 Now,fort>0 consider the function Since F is continuous,under(3.7)and(3.8),it follows that for anyλ∈ (0,γ),there existtα>0 small andxα∈Msuch that SinceMis compact,up to a subsequence,we may assume thatxαconverges to some pointxo∈M. Note first that for allα≥ 0,tα Now,suppose that for allε>0,there existsαε>0 such thatdistg(xα,p)≤εfor allα≥αε.Choosesuch that,tα< which,by virtue of(3.16),is impossible.We deduce then thatxo6=p. Now,let 0<τα<1,forx∈B(τ−1α δg)⊂Rnconsider the sequences Takeταsuch thatCorτα=tα.As in the above lemma,we can easily check that there is a subsequence ofˆνα=ηδ(ταx)ναwhereδis as in the above lemma,that weakly converges in D1,2(IRn)to some functionν,a weak solution on D1,2(IRn)to(3.14).Note that this time the singular term disappears becausexo6=pand because of coursetα→0. It remains to show thatν6=0.For this purpose,take a pointa∈IRnand a constantr>0 such that|a|+r and Co,here,is the constant appearing in inequality(3.9).Since we have we get by construction ofxαthat for suchaandr, Suppose now thatν≡0.Take any functionh∈D1,2(IRn)with support included in a ballB(a,r)⊂IRn,withaandras above.Then,by takingλsmall enough,we get by the same calculation done in(3.15)thatconverges to 0 for alla∈IRnandr>0 such thatIn particular, which makes a contradiction.Thusν6=0. The proof of the remaining statements of the lemma goes in the same way as in lemma 3.4. Proofof Theorem 3.1.First,it is worthy to mention that the valueG∞(v)taken on a nontrivial weak solutionvof the Euclidean equation(3.9)is greater or equal to the constantβ∗.In fact,ifvis solution of(3.9),then by Hardy and Sobolev inequalities we have and then by(3.17)and(3.18)we get Now,letuαbe a sequence of solutions of(Eα)such thatis then a bounded Palais-Smale sequence ofJαat some levelβ.Up to a subsequence,we may assume thatuαconverges weakly in(M)and almost everywhere inMto a solutionuof(E∞).Setvα=uα−u,then by Lemma 3.1,vαis a Palais sequence ofJαat levelβ1=β−J∞(u)+o(1).Ifvα→0 strongly in(M),then the theorem is proved withk=l=0.Ifvα→0 only weakly in(M),then we apply Lemmas 3.3,3.4 and 3.5 to get a new Palais-Smale sequenceat levelβ2≤β1−β∗+o(1).So,eitherβ2<β∗and thenconverges strongly to 0,orβ2≥β∗and in this case we repeat the procedure forto obtain again a new Palais-Smale sequence at smaller level.By induction,after a number of iterations,we obtain a Plais-Smale sequence at a level smaller thanβ∗. ? Corollary 3.1.Suppose that the sequenceuαof weak solutions of(Eα)is such that Then,up to a subsequence,uαconverges strongly in(M)to a nontrivial weak solutionuof(E∞). Proof.By Theorem 3.1,there is a weak solutionuof(E∞)such that,up to a subsequence ofuα,we have and Suppose thatu≡0,if there existsi,1≤i≤ksuch thatvi6=0,then by(3.19)we get thus,vi≡0,∀i,1≤i≤k,case in which Lemma 3.4 applies,that is,there existsνj6=0 such that Hence,u6=0.Furthermore,J∞(u)>0,from which we can conclude thatk=l=0.In particular,uαconverges strongly inH21(M)tou. References [1]D.Cao and S.Peng,A global compactness result for singular elliptic problems involving critcal Sobolev exponent,Transcation of AMS,131(6)(2003),1857–1966. [2]O.Druet,E.Hebbey and F.Robert,Blow-Up Theory for Elliptic PDEs in Riemannian Geometry,Princeton University Press,2004. [3]M.Dellinger,Etude asymptotique et multiplicitpour lquation de Sobolev Poincar,Thesis,University of Paris VI,2007. [4]E.Hebey,Introductionl’analyse non linaire sur les varits,Diderot,1997. [5]F.Madani,Le problme de Yamabe avec singularits et la conjecture de Hebey-Vaugon,Thesis,UniversitPierre et Marie Curie,2009. [6]D.Smet,Nonlinear Schrdinger equations with Hardy potential and critical nonlinearities,Transactions of AMS,357(7)(2004),2909–2938. [7]M.Struwe,A global compactnes result for elliptic boudary value problems involving limiting nonlinearities,Math.Z.,187(1987),511–517. [8]S.Terracini,On positive entire solutions to a class of equations with a singular coefficient and critical exponent,Adv.Differential Equations,1(2)(1996),241–264.
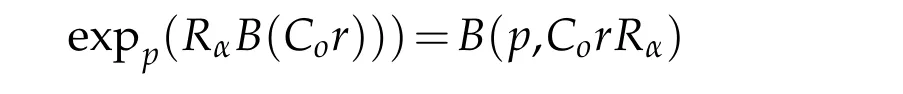
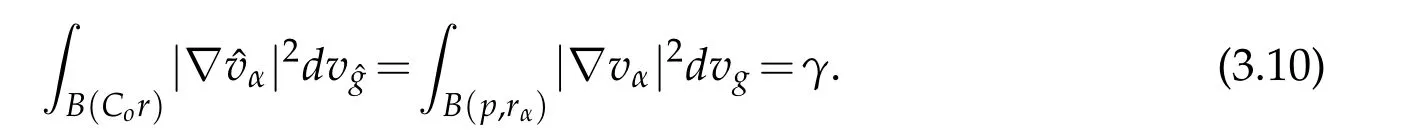

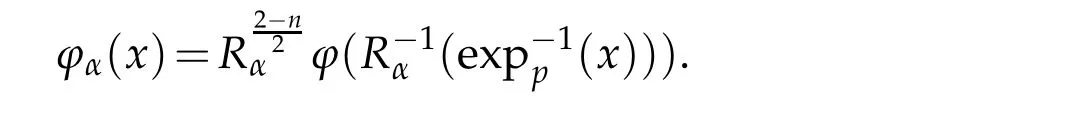
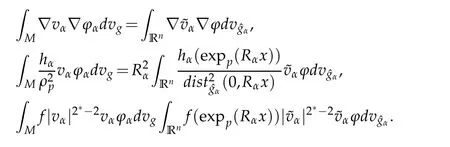
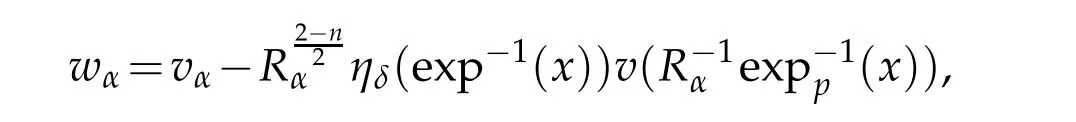
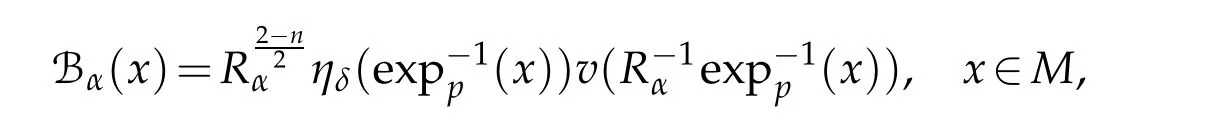
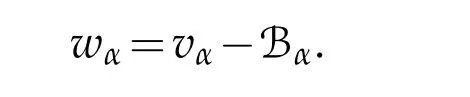


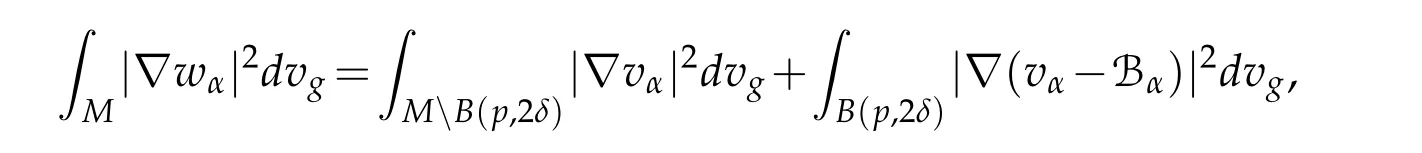
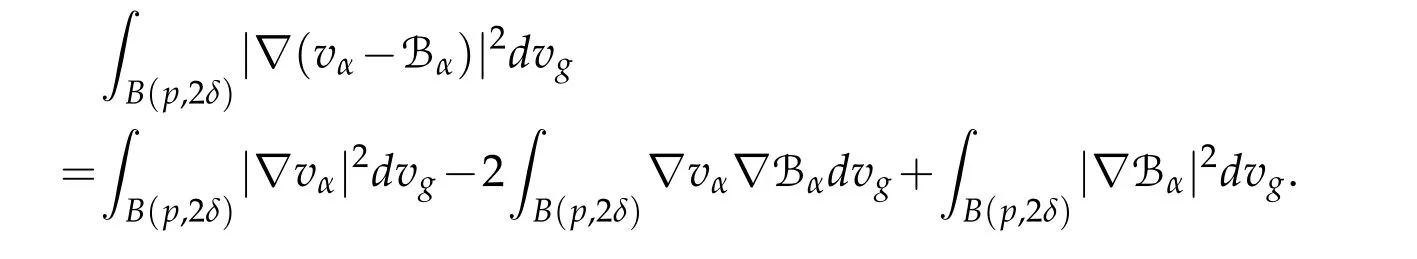
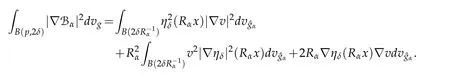

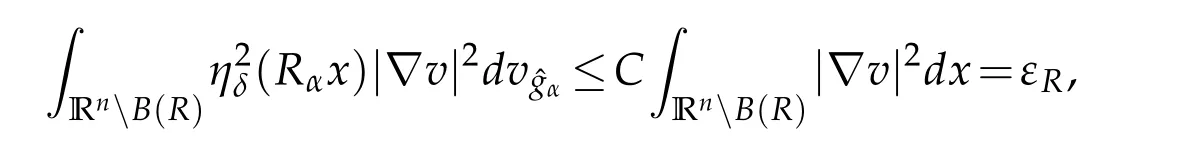
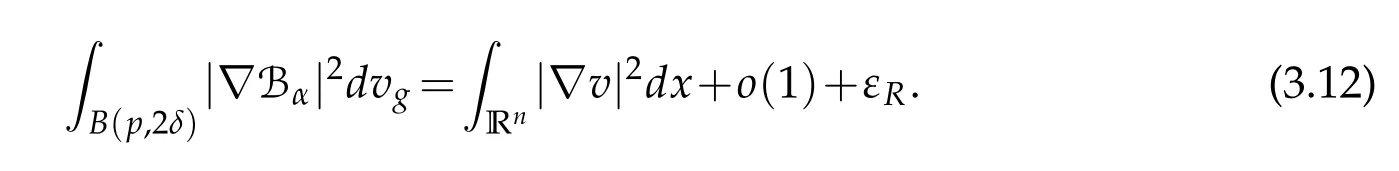

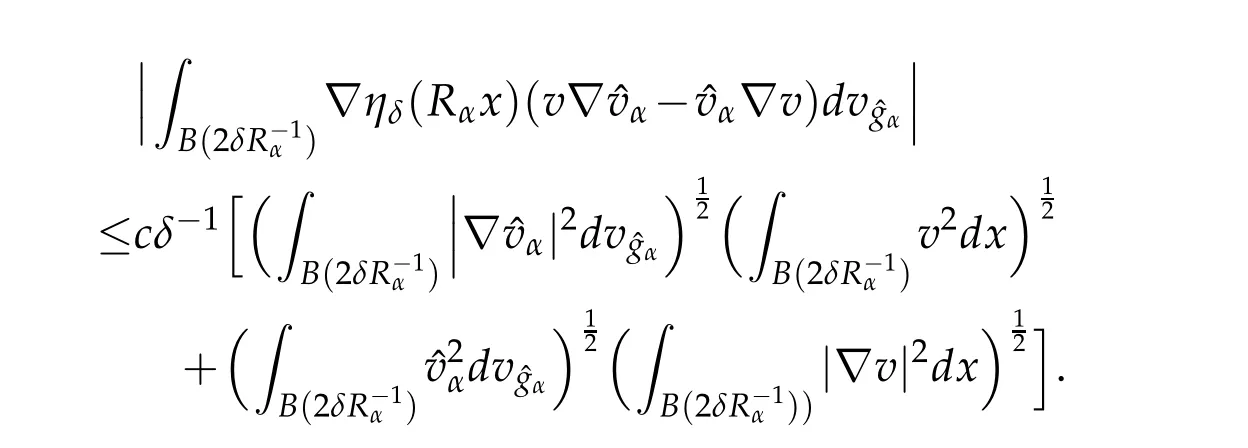
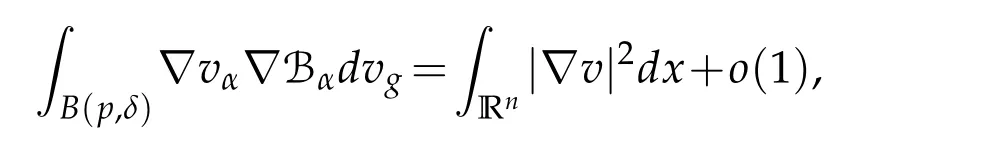
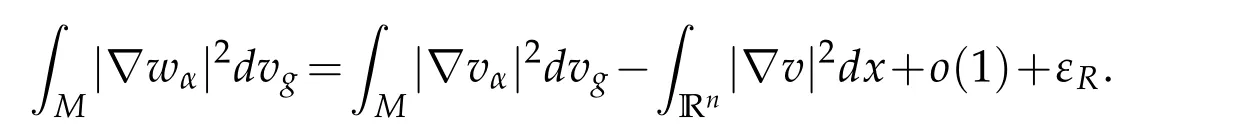
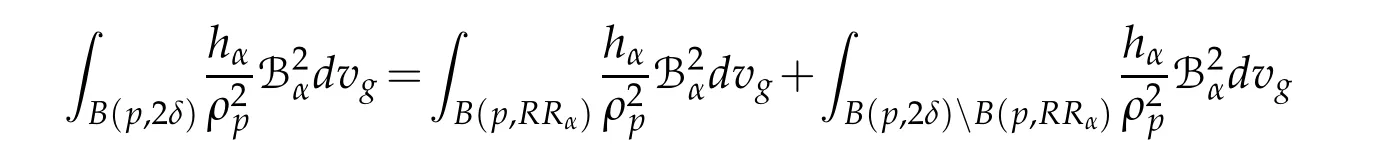
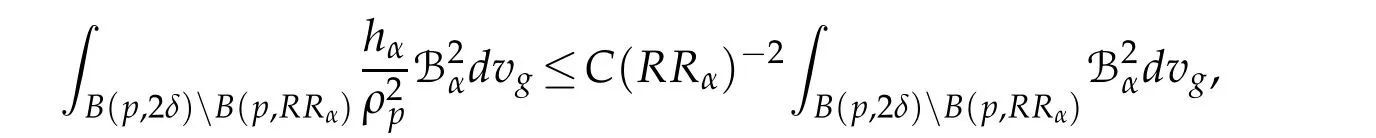
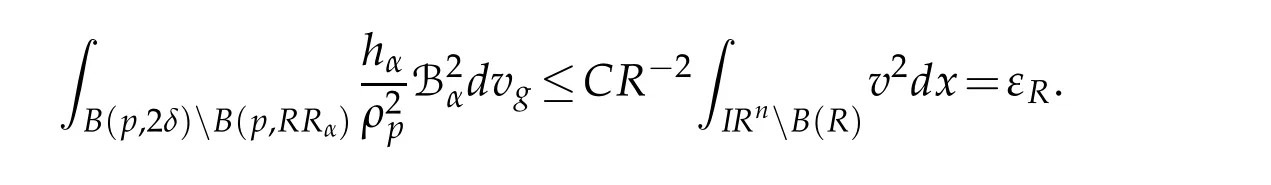
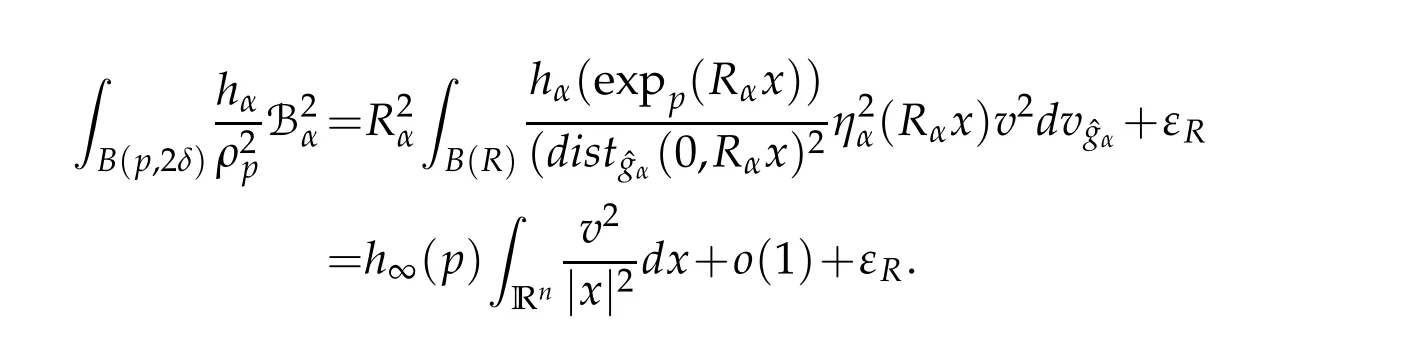
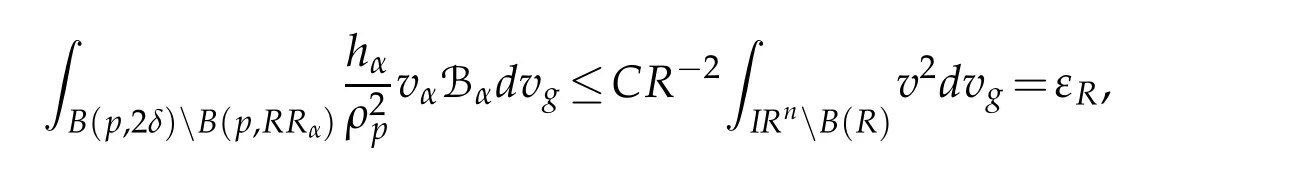
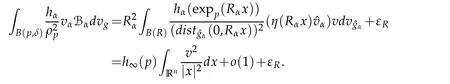
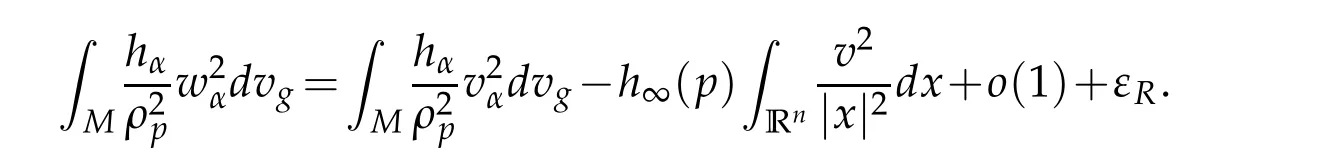
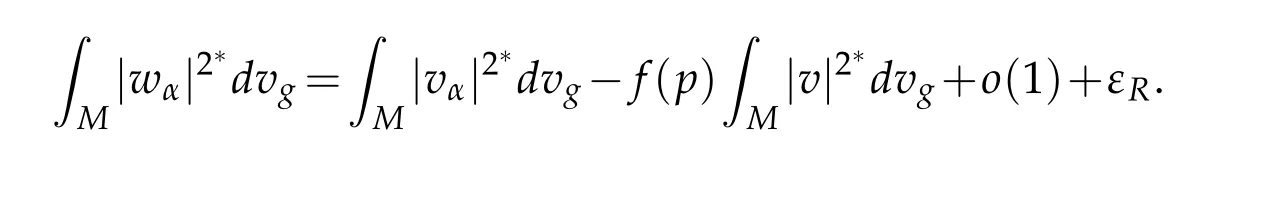

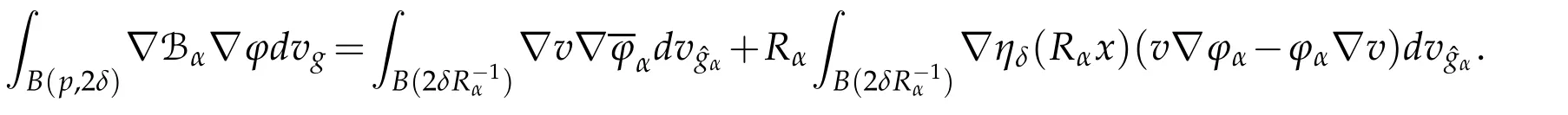
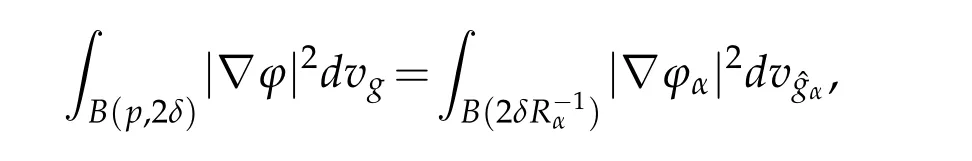
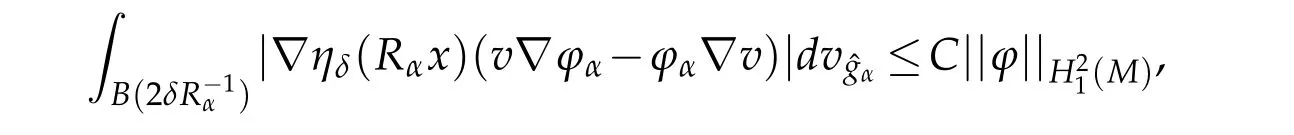

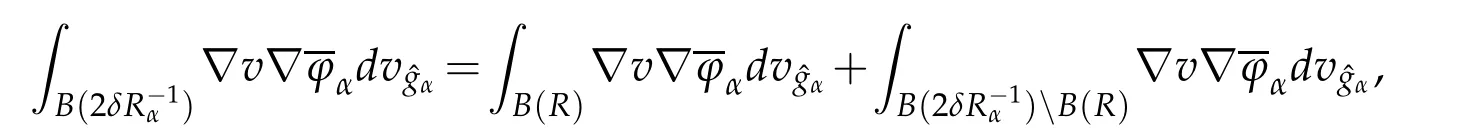
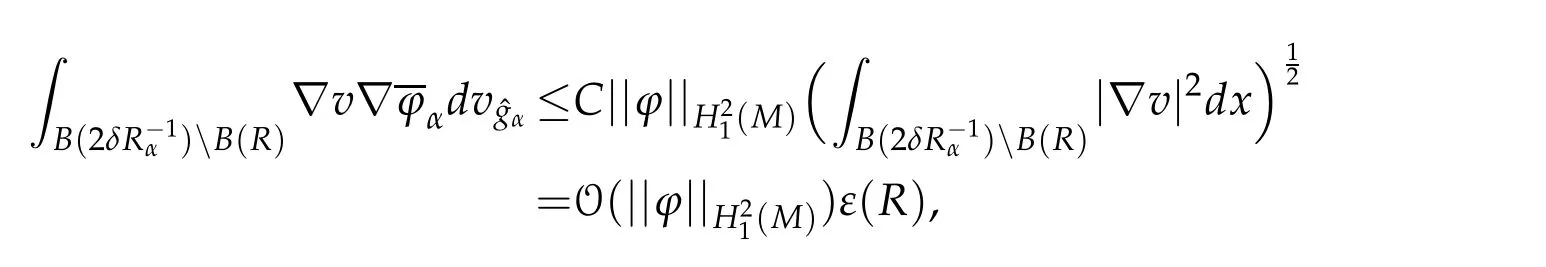
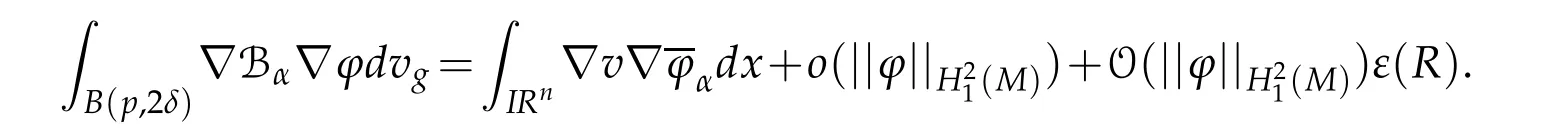
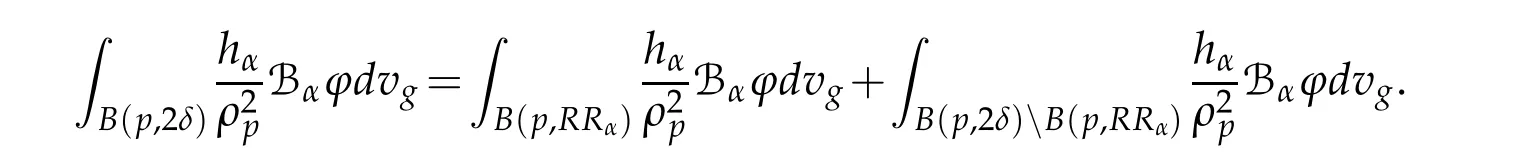
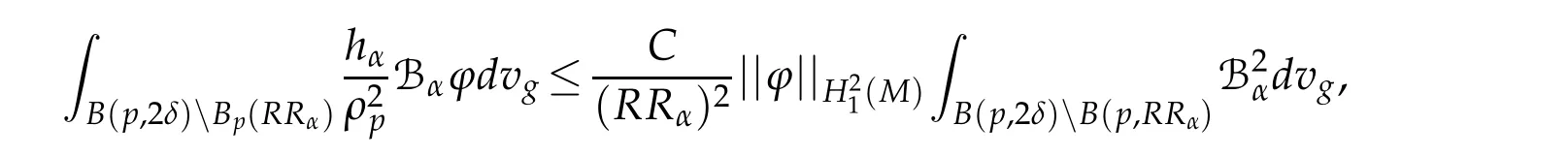
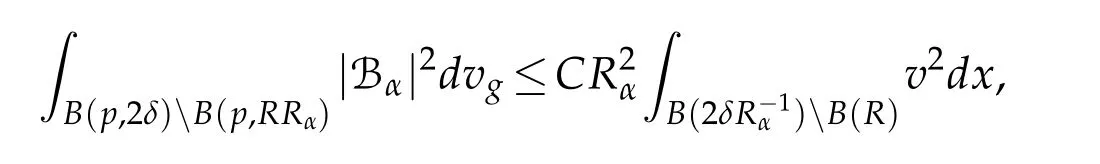
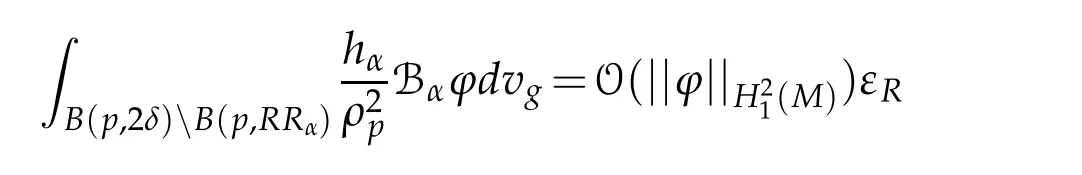
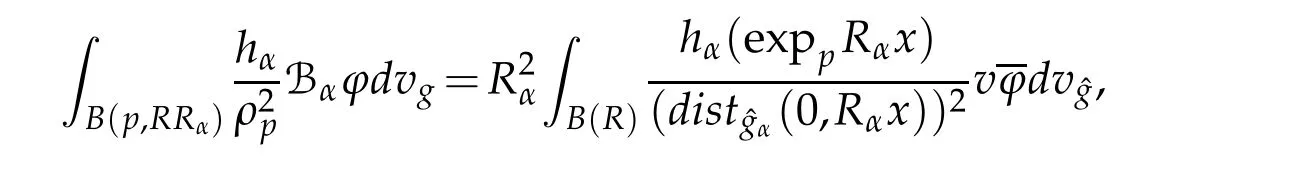

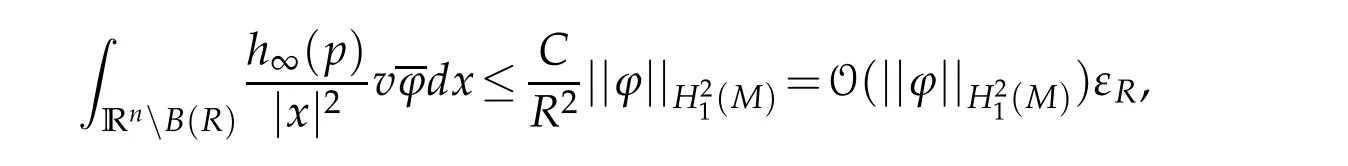
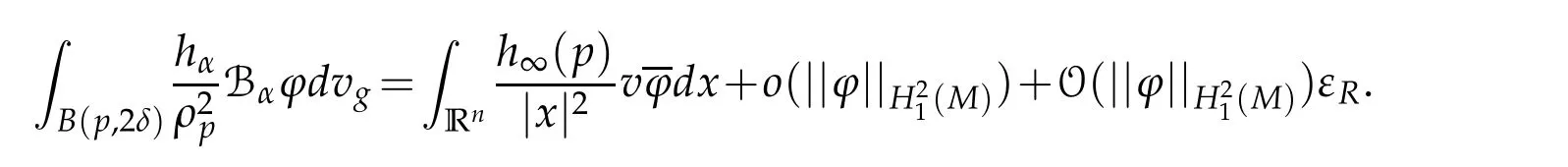
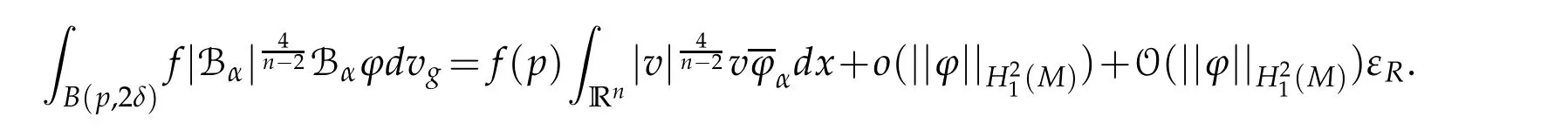
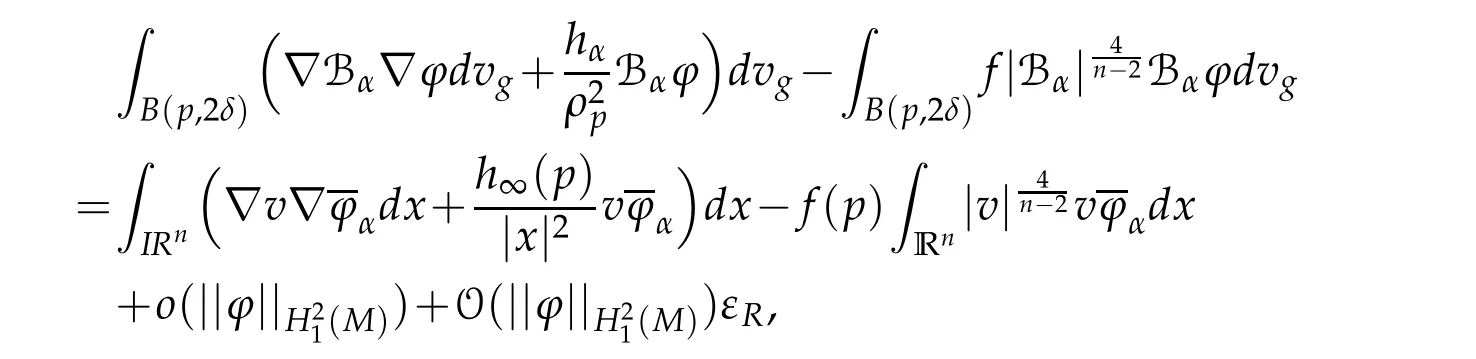
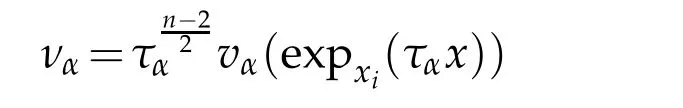

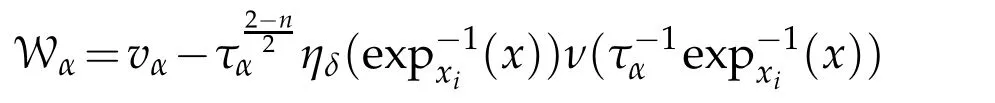
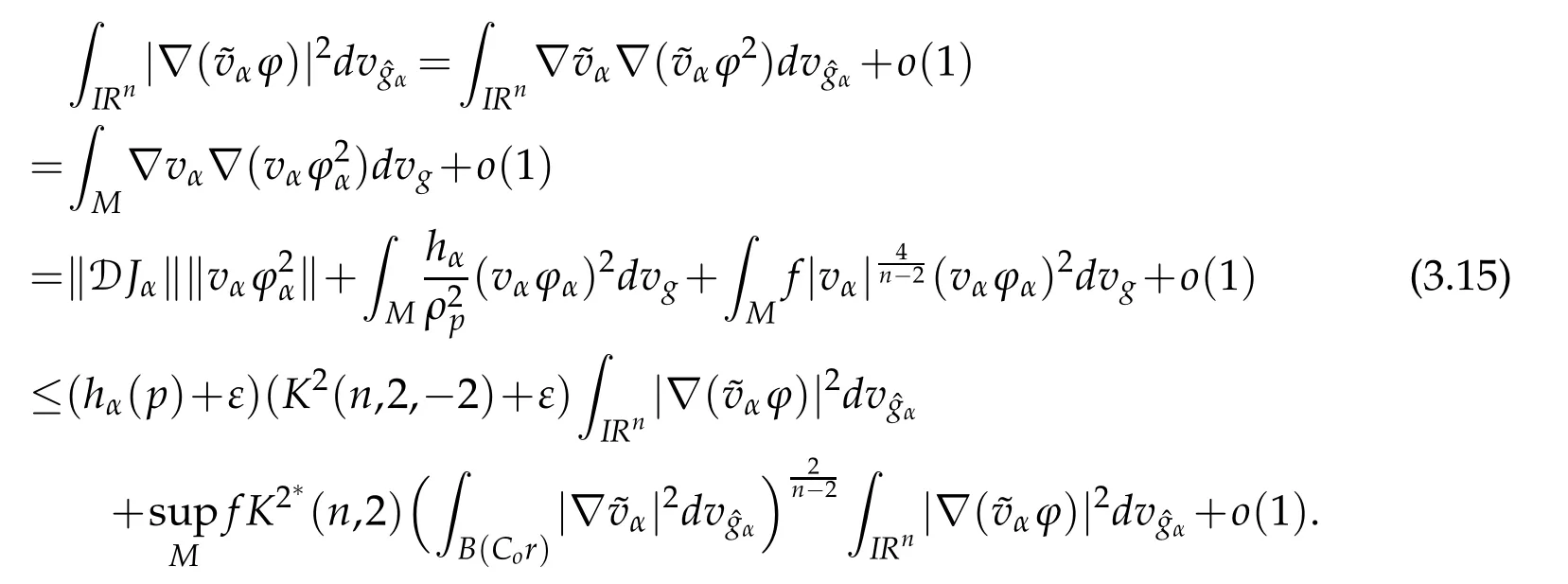

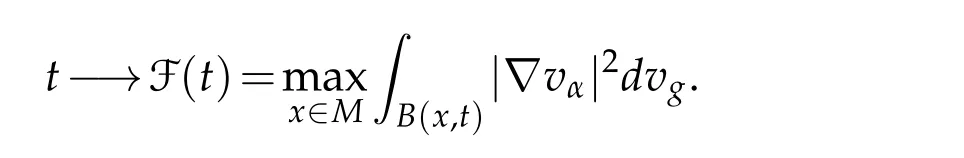
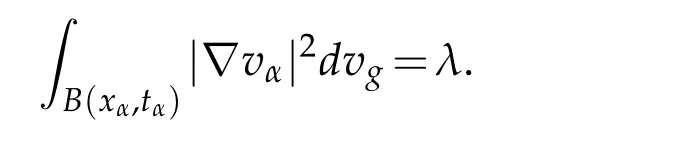
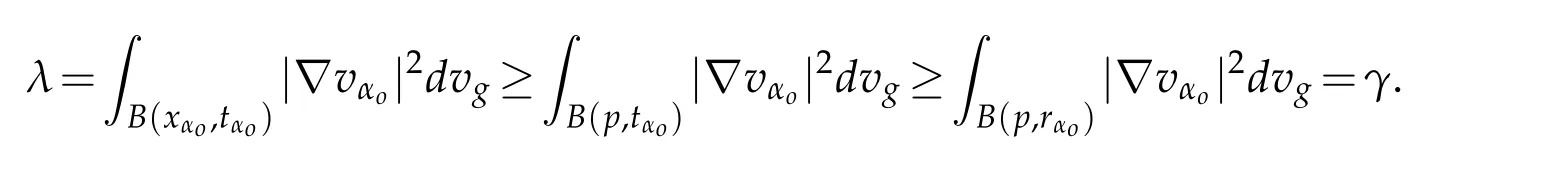
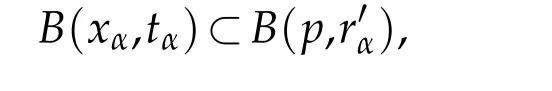
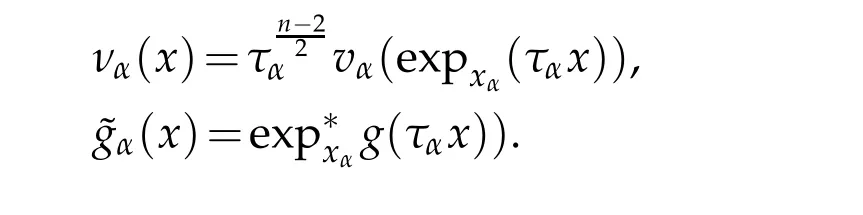
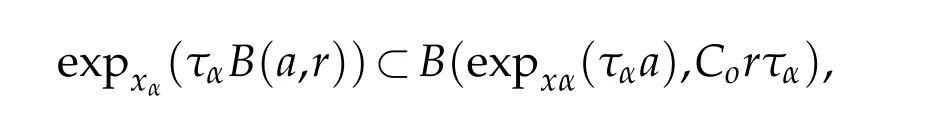
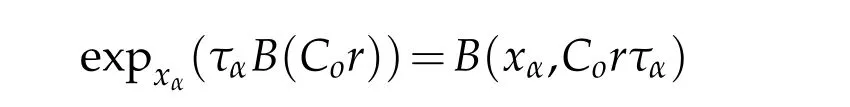
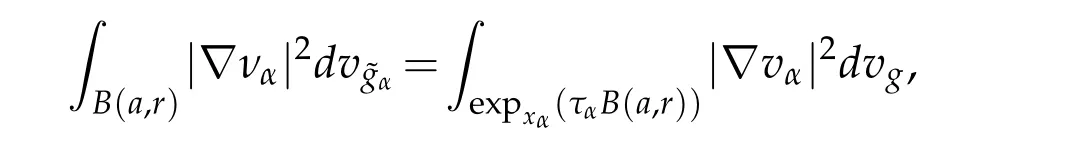
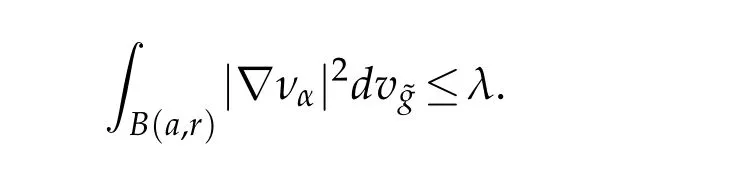
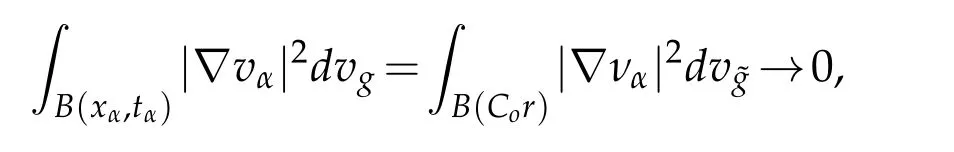
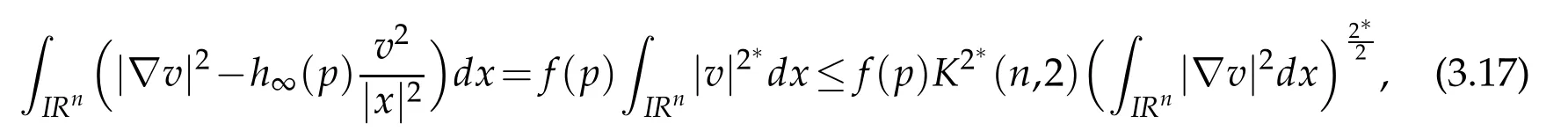
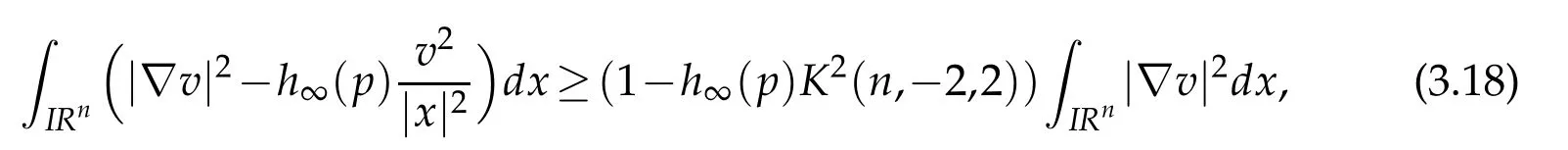
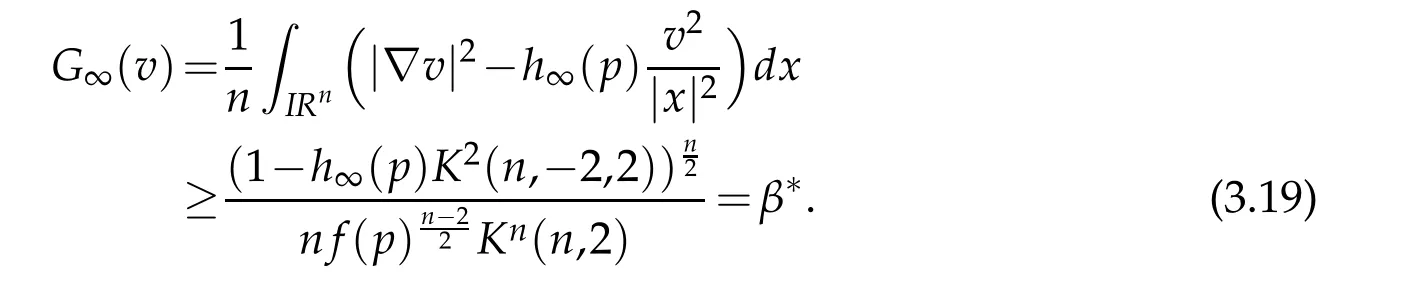
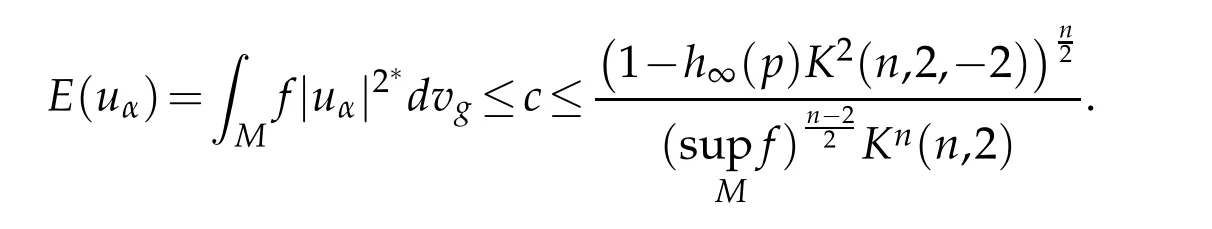
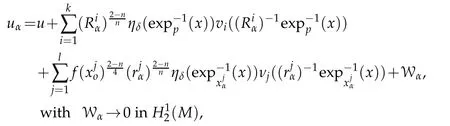
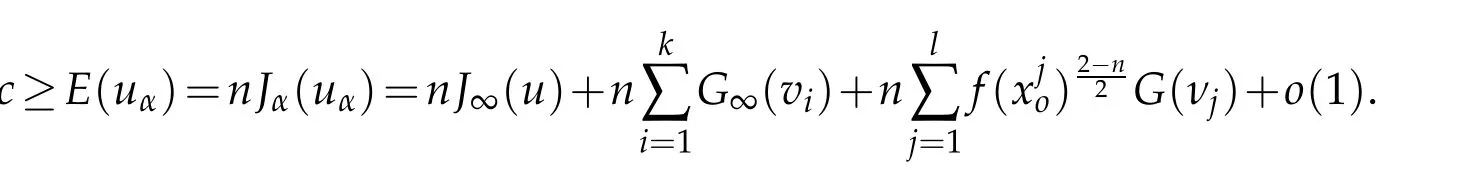
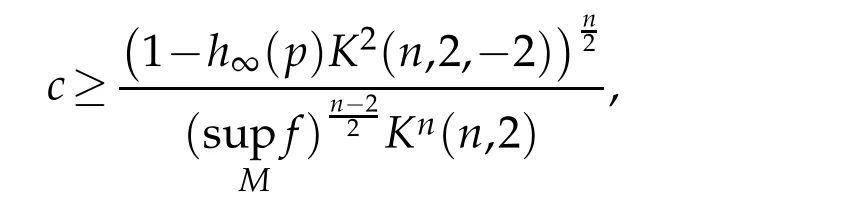
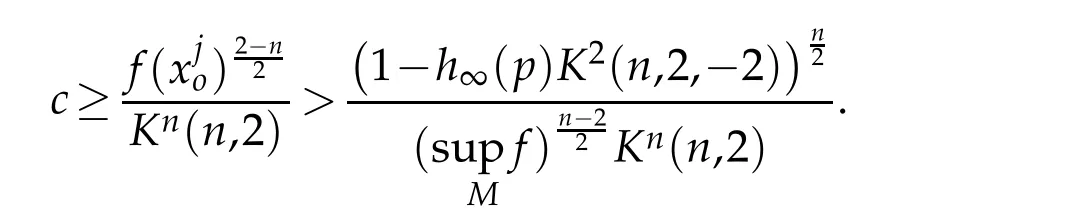
杂志排行
Analysis in Theory and Applications的其它文章
- On Weighted Lp−Approximation by Weighted Bernstein-Durrmeyer Operators
- On an Axiomatic about Functional Means
- Commutators of Singular Integral Operators Related to Magnetic Schrdinger Operators
- Some Generalized q-Bessel Type Wavelets and Associated Transforms
- Approximation for Certain Stancu Type Summation Integral Operator
- On Quasi-Chebyshevity Subsets of Unital Banach Algebras
