考虑经验因素的暴雨频率曲线最优化拟合算法

姬鹏杰 杜坤 冯燕 周明 杜雨

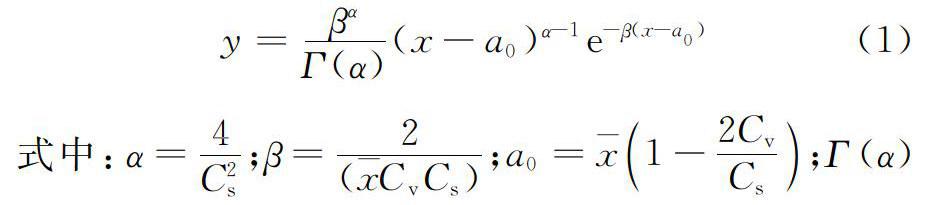
摘要：暴雨频率曲线拟合是推求暴雨强度公式必不可少的步骤，考虑经验因素进行暴雨频率曲线拟合，提出将暴雨强度频率曲线拟合作为最优化问题，采用加权阻尼高斯牛顿迭代算法求解。与已有方法相比，提出引入权重系数以提高工程常用重现期段拟合精度，避免不同历时暴雨频率曲线相交；提出应用有限差分法简化雅克比矩阵计算，并在海塞矩阵对角添加阻尼系数改进迭代收敛。以云南省保山市隆阳区33 a实测降雨资料为例，证明了算法的可行性及实用性。

关键词：暴雨频率曲线；经验因素；最优化；迭代算法

中图分类号：TU992.02 文献标志码：A文章编号：16744764（2018）02007706

收稿日期：20170314

基金项目：国家自然科学基金（51608242）；云南省人才培养计划项目 （14118943）

作者简介：姬鹏杰（1992），男，主要从事市政工程研究，Email：443838096@qq.com。

杜坤（通信作者），男，博士， Email：250977426@qq.com。

Received：20170314

Foundation item：National Natural Science Foundation of China（No.51608242）；Personnel Training Program of Yunnan Province （No.14118943）.

Author brief：Ji Pengjie（1992），main research interest： municipal engineering，Email：860655976@qq.com.

Du Kun （correspondence author）， PhD， Email：250977426@qq.com.Study on optimal fitting algorithm of rainstorm frequency

curve considering the empirical factors

Ji Pengjie1， Du Kun1， Feng Yan1， Zhou Ming1， Du Yu2

（1. Faculty of Civil Engineering and Mechanics， Kunming University of Science and Technology， Kunming 650500， P. R. China；

2. The Third Construction Engineer Company LTD， China Construction Second Engineer Bureau， Wuhan 430022， P. R. China）

Abstract：The rainstorm frequency curve fitting is essential for the identification of storm intensity formula， this paper carried out the study of rainstorm frequency curve fitting with considering of experience factors， and put forward to regard the rainstorm intensity frequency curve fitting as an optimization problem， and then to solve it by the weighted damped GaussNewton iterative algorithm. Compared to existing methods， the proposed method introduced weight coefficients to improve the fitting precision of commonly used recurrence period in engineering， and to avoid the intersection problem of different frequency curves. The finite difference method is proposed to simplify the calculation of Jacobian matrix， and the damping coefficient was added in Hesse matrix to improve iterative convergence. Thirtythree years of rainfall data of Longyang District of Baoshan city in Yunnan Province were used as an example to illustrate and demonstrate the feasibility and practicability of the proposed algorithm.

Keywords：rainstorm frequency curve； empirical factors； optimization； iterative algorithm

近年來，中国城镇内涝灾害频发，极大危害了人们的生命财产安全[1]。在开展雨水管网设计、调蓄工程规划时，许多城镇目前仍采用1987版《室外排水设计规范》规定的暴雨强度公式。随着城市化进程加速及全球气候持续变暖，各地区降雨特性发生了较大变化，1987版规范的公式存在推源数据过旧、无法合理反映降雨特征的问题，因此，有必要对暴雨强度公式进行修编。暴雨频率曲线拟合是推求暴雨强度公式必不可少的步骤，其通过假定降雨强度与频率服从某一理论函数分布，采用实测数据对函数中的参数进行拟合，进而实现降雨强度与降雨频率关系外延计算，并消除测量误差影响、防止参数过拟合。

常用的暴雨频率曲线包括皮尔逊III型分布曲线（PIII型曲线）、耿贝尔和指数分布曲线。耿贝尔和指数分布曲线是PIII型曲线在Cs=1.14和Cs=2时的特例，计算相对简单，但拟合精度不高；PIII型频率曲线拟合精度高，但计算复杂。针对PIII型曲线离均系数计算速度慢、精度低的问题，Che[2]应用Excel软件简化计算，王正发[3]指出Excel计算时存在数字发散区，提出应用Matlab软件计算离均系数。针对暴雨频率曲线拟合，Balin[4]通过标准化降水指数模型提高计算效率，崔俊蕊等[5]利用水文频率分析软件简化试线过程，Mandal等[6]引入马尔可夫链模型进行拟合，Wu等[7]引入置信区间法提高拟合精度。上述研究在提高计算效率及拟合精度两个方面取得了一定成果，但高琳等[8]的最新研究指出，目前大多数研究都忽视了实践工程经验因素，将暴雨频率曲线拟合作为单纯的参数求解问题。高琳等[8]还提出，对于暴雨强度频率曲线拟合，并非误差越小越好，而应更多地照顾工程实际要求重现期段下的样本，这样得到的暴雨强度公式更加符合实际工程需求。值得注意的是，高琳等虽然给出了参数拟合准则，但未提出相应算法，其通过反复适线拟合参数，这导致了巨大计算工作量。在考虑经验因素的情况下，如何高效实现暴雨频率曲线参数拟合是值得研究的问题。

笔者将暴雨强度频率曲线拟合作为最优化问题，提出加权阻尼高斯牛顿迭代算法进行求解。与已有方法相比，该算法引入权重系数提高工程常用重现期段拟合精度，通过调节权重系数避免不同历时理论频率曲线相交问题；再者，采用有限差分法简化雅克比矩阵计算，并在海塞矩阵对角添加阻尼系数改进迭代收敛，避免了反复适线导致的巨大计算工作量。以云南省保山市隆阳区1981—2013年间33 a实测降雨资料为例，证明算法的可行性与实用性。

第2期 姬鹏杰，等：考虑经验因素的暴雨频率曲线最优化拟合算法1基于最优化的暴雨频率曲线参数拟

合框架选择PIII型曲线作为理论暴雨频率曲线，其密度函数为y=βαΓ（α）（x-a0）α-1e-β（x-a0）（1）式中：α=4C2s；β=2（CvCs）；a0=（1-2CvCs）；Г（α）为伽玛函数；x、Cv和Cs分别为均值、偏差系数及偏态系数。将参数拟合作为优化问题，目标函数可写为f（x，Cs，Cv，tp）=（Xp-p）TW（Xp-p）（2）式中：Xp为实测暴雨强度，为n×1的列向量，n为数据采集年限；W为权重系数矩阵；p为对应的理论暴雨强度。在Matlab环境下，理论暴雨强度p可采用式（3）计算。p=h（x，Cv，Cs，Τp）=

1βgaminv（1-Τp，α，1）-a0（3）式中：Tp為降雨频率，其中元素tp=m（n+1），m为实测暴雨强度从大到小排列的年序次。目标函数的物理意义是求取参数x、Cv和Cs使理论暴雨强度p与实测值Xp间均方差最小，并引入权重系数矩阵W提高工程常用段降雨频率下拟合精度。由于理论暴雨强度p与参数x、Cv和Cs非线性相关，故需采用迭代法求解优化问题[9]。笔者采用阻尼高斯牛顿迭代法进行求解[10]，基本思路是采用参数的矩估计值作为初始值，通过计算雅克比矩阵构造搜索向量，沿目标函数减小方向修正参数，并在海塞矩阵对角添加阻尼系数改进迭代收敛性。为便于推导，记κ=[x，Cv，Cs]，第k次迭代的解为f（κk+Δκk，Τp）=[Xp-h（κk+Δκk，Τp）]T·

W[Xp-h（κk+Δκk，Τp）]（4）式（4）的一阶线性展开式为f（κk+Δκk，Τp）=[ΔXkp-J（κk，Τp）Δκk]T·

W[ΔXkp-J（κk，Τp）Δκk]（5）式中：ΔXkp=Xp-h（κk，Τp），雅克比矩阵J（κ，Τp）=[pxpCvpCs]，为n×3矩阵。

由于理论暴雨强度计算涉及伽玛函数和不完全伽玛函数运算，使得雅克比矩阵解析式推导非常复杂。采用有限差分法计算雅克比矩阵，如式（6）所示。px=h（x+Δx，Cv，Cs，Tp）-h（x，Cv，Cs，Tp）Δx

pCv=h（x，Cv+ΔCv，Cs，Tp）-h（x，Cv，Cs，Tp）ΔCv

pCs=h（x，Cv，Cs+ΔCs，Tp）-h（x，Cv，Cs，Tp）ΔCs（6）理论上，在进行有限差分计算时，式（6）中Δ、ΔCv、ΔCs的取值越小，计算结果越接近解析解，但取值过小会超出计算机计算精度，反而导致不准确的计算结果[11]。经过尝试，在差分过程中，推荐Δx=0.001，ΔCv=0.01，ΔCs=0.01。根据多元函数极值理论，当目标函数取得极小值时，应有f（κk+Δκk，Τp）Δκk=-2J（κk，Τp）T·

W[ΔXkp-J（κk，Τp）Δκk]=0（7）根据式（7）可得Δκk=[J（κk，Τp）TWJ（κk，Τp）]-1J（κk，Τp）TWΔXkp（8）为改进迭代收敛性，在海塞矩阵的对角添加阻尼系数矩阵Γ[12]，可得Δκk=[J（κk，Τp）TWJ（κk，Τp）+Γ]-1·

J（κk，Τp）TWΔXkp（9）在参数拟合过程中，可设置阻尼系数Γ的取值随迭代次数的增加而减小，拟合框架如图1所示。

图1暴雨频率曲线参数拟合框架图

Fig. 12算例分析

算例分析旨在利用实际降雨数据阐明：1）调节权重系数提高工程常用段拟合精度；2）调节权重系数避免暴雨频率曲线相交；3）添加阻尼系数改进迭代收敛性。值得说明的是，该工程是短历时排水系统，但所提出方法同样适用于长历时排涝系统的暴雨频率曲线拟合。

2.1调节权重系数提高工程常用段拟合精度

通过收集云南省保山市隆阳区1981—2013年间33 a实测降雨数据，整理出5、10、15、20、30、45、60、90、120、150、180 min共11个降雨历时下的暴雨强度。对拟合结果进行分析发现，不同暴雨强度的拟合精度不同，降雨历时越小，拟合精度越低。例如，5、10 min的拟合精度远低于150、180 min拟合精度，其原因是降雨历时越小，暴雨强度离均系数越大，尤其对最大值与最小值，往往偏离拟合曲线较远，如图2所示。以图2中5 min降雨历时下暴雨强度为例，阐明通过调节权重系数，提高工程常用重现期段拟合精度。

图2调节权重系数提高工程常用段拟合精度示意图

Fig. 2如图2中曲线a所示，当设置权重矩阵W中所有元素为1时，即采用普通的高斯牛顿法求解优化问题[13]，此时残差Δφ=Xp-p2n=0.088，整体拟合最佳，工程常用重现段拟合残差Δφ=0062。为进一步提高工程常用段拟合精度，减小其他段权重系数并保持工程常用段权重系数不变，表1给出了调整权重系数时残差变化情况。表1调整权重系数时残差变化情况

Table 1权重系数工程常用段其它段整体残差工程常用

段残差对应曲线110.0880.062a10.50.0890.060b10.250.0900.059c10.062 50.0920.055d

如表1所示，随着其他段权重系数减小，整体残差增大，工程常用段残差减小；对应于图2，曲线逐步向下偏移，使得适线结果与工程常用段样本点更贴近。由此可见，通过改变权重系数能对适线结果进行微调，有效提高工程常用重现期段拟合精度。但值得说明的是，提高工程常用段拟合精度时，整体精度会不可避免的下降，且不同案例的精度变化不同。如果要定量给出精度取值或取值范围，需要收集多个城市降雨数据进行综合分析，这是一个工作量巨大的研究。鉴于笔者的目的在于证明所提出的算法能高效调整二者精度，故不对上述问题进行深入分析。

2.2调节权重系数避免理论频率曲线相交

采用传统高斯牛顿迭代法进行参数拟合，即设置权重矩阵W中所有元素值为1，将各历时适线结果绘制在同一海森机率格图上。如图3所示，20 min与30 min降雨历时下理论频率曲线出现相交趋势，这有悖于暴雨强度随历时增大而减小这一基本前提，明显不合理。由此可见，如果简单地将暴雨频率曲线拟合作为数学问题求解，可能导致理论频率曲线相交这一不合理结果。针对该问题，可通过改变权重系数对适线结果进行微调，使理论频率曲线不相交，如图4所示。

图3不同历时下理论频率曲线相交

Fig. 3图4调节权重系数使频率曲线不相交

Fig. 42.3添加阻尼系数改进迭代收敛

高斯牛顿迭代法的收敛性与初值选取相关，一般只有当初值比较靠近真值时才能保证迭代收敛[14]。以5 min降雨历时下暴雨强度频率曲线拟合为例，采用矩估计值作为参数x、Cv、Cs的初值，应用高斯牛顿迭代法求解优化问题。如图5所示，迭代到第6步时，程序提示矩阵奇异、计算不精确，迭代发散、运算终止。

图5普通高斯牛顿迭代法收敛情况

Fig. 5在海塞矩阵对角添加阻尼系数，如式（9）所示，阻尼系数初值取1，分别采用一次方衰减（1/k）及二次方衰减（1/k2）进行算法测试，其中k为迭代次数[15]。

如图6所示，当阻尼系数一次方衰减时，迭代49次达到收敛精度要求（ε<10-4）；当阻尼系数二次方衰减时，迭代33次达到收敛精度要求。虽然二次方衰减法能更快的达到收敛精度，但当初值偏离真值较远时，不能保证迭代收敛[16]。建议先采用二次方衰减法进行初算，若迭代不收敛，则采用一次方或更低衰减方式，可加大阻尼系数初值进一步改进迭代收敛性。

图6添加阻尼系数改进迭代收敛

Fig.62.4基于差分进化算法的优化精度检验

优化问题的求解方法分为确定性算法与随机搜索算法。采用基于梯度信息的确定性搜索算法，其特点是计算效率高，但可能陷入局部最优解。差分进化算法属于随机搜索类算法，其特点是计算量大，但通过多次运算能逼近全局最优解[17]。为检验所提出算法优化精度，通过多次运行差分进化算法进行对比。限于篇幅以5 min降雨历时下暴雨强度数据为例，将差分进化算法运行100次，给出目标函数残差最小的10个解与所提出算法解进行对比。其中，差分进化算法的种群规模取30，3个参数的搜索范围均为[0 10]，变异因子F=0.6，交叉因子Cr=0.6，最大迭代次数G=100。两种算法优化结果及目标函数残差如表2，其中A算法为加权阻尼高斯牛顿迭代算法，B算法为差分进化算法。表2二种算法优化结果及目标函数残差

Table 2 算法均值mCvCs目标函数残差AB1.695 8820.284 8012.849 5360.088 2621.695 7580.284 8342.849 4380.088 2621.695 9360.284 8162.848 0230.088 2621.695 8510.284 6972.846 2250.088 2621.695 8550.284 8002.847 4490.088 2621.695 8340.284 8192.850 060.088 2621.695 8680.284 7692.847 7930.088 2621.695 8650.284 7622.848 2600.088 2621.695 868 0.284 758 2.847 301 0.088 262 1.695 948 0.284 763 2.848 609 0.088 262 1.695 806 0.284 841 2.848 003 0.088 262

如表2所示，為对比计算精度，将结果保留6位小数。其中加权阻尼高斯牛顿迭代法优化所得的目标函数残差为0.008 826 2，差分进化算法逼近的全局最优解的目标函数残差也为0.008 826 2。虽然参数优化结果有一定差异，但差异均小于10-3，从工程应用角度来看，上述差异可以忽略。因此，可以认为加权阻尼高斯牛顿迭代算法能获得全局最优解。

3结论

研究了考虑经验因素时的暴雨频率曲线拟合算法，以云南省保山市隆阳区33 a实测降雨资料为例论证了算法的可行性，得到如下结论：

1）在利用传统的高斯牛顿法进行暴雨频率曲线拟合时，迭代可能不收敛，且存在不同历时暴雨频率曲线相交的问题；

2）通过在海塞矩阵对角添加阻尼系数能保证高斯牛顿迭代法的收敛，建议采用阻尼系数二次方衰减进行暴雨频率曲线拟合。

3）通过调节权重系数能方便对适线结果进行微调，避免不同历时暴雨频率曲线相交的问题，并提高工程常用重现期段拟合精度，但如何平衡工程常用段与整体精度需要进一步研究。

4）由于PIII型曲线涉及伽玛函数和不完全伽玛函数运算，雅克比矩阵解析式推导繁复，建议采用有限差分法简化计算，推荐Δ=0.001，ΔCv=001，ΔCs=0.01。

5）采用差分进化算法搜索全局最优解，验证了所提出的加权阻尼高斯牛顿算法同样能获得全局最优解。文中所有涉及运算都进行了编程，程序运算时间小于10 s，使繁复的适线工作能在5～10 min完成。

参考文献：

[1] 车伍， 杨正， 赵杨，等. 中国城市内涝防治与大小排水系统分析[J]. 中国给水排水， 2013， 29（16）： 1319.

CHE W， YANG Z， ZHAO Y， et al. Analysis of urban flooding control and major and minor drainage systems in China [J]. China Water & Wastewater， 2013， 29（16）：1319. （in Chinese）

[2] CHE G W. PearsonIII frequency curve plotting in Excel table [J]. Applied Mechanics & Materials， 2014， 556562： 58295834.

[3] 王正发. MATLAB在PⅢ型分布离均系数p值计算及频率适线中的应用[J]. 西北水电， 2007（4）： 14.

WANG Z F. MATLAB programming language used to calculate variation coefficient p of the PIII distribution and fit a frequency curve [J]. Northwest Hydropower， 2007（4）： 14. （in Chinese）

[4] BLAIN G C. Standardized precipitation index based on pearson type III distribution [J]. Revista Brasileira De Meteorologia， 2014， 26（2）：167180.

[5] 崔俊蕊， 王政然， 梁爽，等. 城市设计暴雨频率曲线的拟合及参数优化[J]. 水电能源科学， 2014（11）： 4851.

CUI J R， WANG Z R， LIANG S， et al. Fitting and parameter optimization of urban design storm frequency curve [J]. Water Resources and Power， 2014（11）： 4851. （in Chinese）

[6] MANDAL K G， PADHI J， KUMAR A， et al. Analyses of rainfall using probability distribution and Markov chain models for crop planning in Daspalla region in Odisha， India [J]. Theoretical and Applied Climatology， 2015， 121（3）：517528.

[7] WU Y C， LIU J J， SU Y F， et al. Establishing acceptance regions for Lmoments based goodnessoffit tests for the Pearson type III distribution [J]. Stochastic Environmental Research and Risk Assessment， 2014， 26（6）： 873885.

[8] 高琳， 周玉文， 唐颖， 等. 城市暴雨強度公式皮尔逊Ⅲ型适线问题研究[J]. 给水排水， 2016（8）： 4751.

GAO L， ZHOU W Y， TANG Y， et al. Research on the fitting of pearson type III in urban storm water intensity equation [J]. Water & Wastewater Engineering， 2016（8）： 4751. （in Chinese）

[9] RAFIQ A， RAFIULLAH M. Some multistep iterative methods for solving nonlinear equations [J]. Computers & Mathematics with Applications， 2009， 58（8）： 15891597.

[10] FAIRBANK M， ALONSO E. Efficient calculation of the GaussNewton approximation of the Hessian matrix in neural networks [J]. Neural Computation， 2012， 24（3）： 607610.

[11] ZHANG J， GENG X， DAI R. Analysis on two approaches for high order accuracy finite difference computation [J]. Applied Mathematics Letters， 2012， 25（12）： 20812085.

[12] HAN Q， ZHANG Q S. An upper bound for hessian matrices of positive solutions of heat equations [J]. The Journal of Geometric Analysis， 2016， 26（2）： 715749.

[13] ERINA M Y，IZMAILOV A F. The GaussNewton method for finding singular solutions of systems of nonlinear equations [J]. Anz Journal of Surgery， 2015， 58（2）： 395405.

[14] PHAN A H， TICHAVSKY P， CICHOCKI A. Low complexity damped GaussNewton algorithms for CANDECOMP /PARAFAC[J]. Siam Journal on Matrix Analysis& Applications， 2013， 34（1）： 126147.

[15] SHEHU Y. Iterative method for fixed point problem， variational inequality and generalized mixed equilibrium problems with applications [J]. Journal of Global Optimization， 2013， 52（1）： 5777.

[16] JIN Q. Further convergence results on the general iteratively regularized GaussNewton methods under the discrepancy principle [J]. Mathematics of Computation， 2013， 82（283）： 16471665.

[17] MACIEL L， GOMIDE F， BALLINI R. A differential evolution algorithm for yield curve estimation [J]. Mathematics & Computers in Simulation， 2016， 129：1030.