压力型可回收式锚杆锚固段应力分布

唐士鑫 阴可 刘汉龙

摘要：利用弹性力学理论计算了锚固体因轴向压缩导致径向膨胀而产生的径向应变，并与土力学理论相结合计算出砂浆体挤压周围岩土体产生的径向应变。根据锚固体与周围岩土体边界面上的变形协调假定，导出了压力型可回收式锚杆锚固段应力分布的理论解，并与现有理论结果进行对比。结果表明：理论解比现有理论结果更加贴近实际。基于理论解讨论了锚固体与岩土体弹性模量之比E1/E2、岩土体泊松比μ、锚固体外半径R对锚固段上的峰值剪应力及其应力分布范围的影响。结果表明：E1/E2、R越小，μ越大，峰值剪应力越大，剪应力分布范围越小。

关键词：压力型可回收式锚杆；锚固段；径向变形

中图分类号：TU473.1 文献标志码：A文章编号：16744764（2018）02000105

收稿日期：20170314

作者简介：唐士鑫（1992），男，主要从事新型可回收式锚杆研究，Email：20105980@cqu.edu.cn。

阴可（通信作者），男，教授，博士生导师，Email：yinke@cqu.edu.cn。

Received：20170314

Author brief：Tang Shixin（1992），main research interest：recoverable anchor，Email：20105980@cqu.edu.cn.

Yin Ke（corresponding author），professor，PhD supervision，Email：yinke@cqu.edu.cnStudy on distribution of stress along bonded length of

pressure type recoverable anchor

Tang Shixin，Yin Ke，Liu Hanlong

（College of Civil Engineering；Key Laboratory of New Technology for Construction of Cities in

Mountain Area， Ministry of Education， Chongqing University， Chongqing 400030， P.R.China）

Abstract：Based on elastic mechanics and soil mechanics theory and radial deformation coordination conditions between the anchor body outer and the surrounding rock， the distribution formulas of stress along the bonded length of pressure type recoverable anchor were derived. Compared with existing theoretical results，the formulas were proved to be more practical. The peak value and range of shear stress were analyzed with various of the ratio of the anchor bodys elastic modulus to the rocksoil bodys E1/E2 and the poissons ratio of rocksoil body μ and anchor bodys outer radius R， Results show that E1/E2 and R are opposite to the value of peak shear stress but positive to shear stress range while μ is on the contrary.

Keywords：pressure type recoverable anchor；bonded length；radial deformation

自21世紀以来，在提倡建筑节能的大环境下，可回收式锚杆以其独有的经济性、环保性、可回收性优势得到了广泛的关注，不少学者发明了一些专利技术[13]。然而，目前对可回收式锚杆锚固机理的研究还处于初始阶段，工程应用中采用的设计方法非常保守，在一定程度上阻碍了其应用。很多学者从理论和试验上探索了可回收式锚杆的锚固特性。王国庆等[4]设计了与气囊相结合的新型可回收锚杆；Guo[5]模拟分析了可回收树脂锚杆的锚固特性；Li等[67]以深基坑支护结构为工程背景，模拟分析了可回收锚杆的可靠性；Zhang[8]通过工程实验验证了可回收锚杆的适用性；范浩等[9]对一种新型胀壳式锚杆的锚固效果进行数值模拟；Chen等[10]基于有限元模型分析了大直径可回收锚杆的锚固特性，并探讨了相关因素的影响；庞有师等[11]利用弹性半空间体在圆形均布荷载作用下的位移解，推导出可回收锚杆锚固段的应力分布数值解，并在南京燕子矶中学边坡地质灾害治理工程中做了锚杆的抗拔试验研究[12]。

由于可回收式锚杆的种类多种多样[13]，本文以压力型可回收式锚杆[14]（构造见图1）为研究对象，利用弹性力学和土力学理论推导可回收式锚杆锚固段上应力的分布规律，分析该锚杆的力学特性以及影响因素。

图1压力型可回收式锚杆构造形式

Fig.1Structure system of pressure type recoverable bolt1求解锚固段应力分布

第2期 唐士鑫，等：压力型可回收式锚杆锚固段应力分布1.1基本假定

从图1所示压力型可回收式锚杆的构造图可以看出，受拉锚杆通过承载体压缩空心圆柱状的砂浆体并使其发生膨胀，挤压周围岩土体（本文所说的岩土体仅包含“土体”和“软岩”两种介质）并产生摩擦力，这构成了压力型可回收式锚杆的锚固基础。

为了研究方便，作如下假设：1）锚固体与岩土体均为均匀、连续、各向同性的线弹性体；2）锚固体截面上的轴向应力σz呈均匀分布；3）在砂浆体与周围岩土体相互作用过程中，岩土体处于弹性状态，且两者径向变形连续；4）岩土体与锚固体的界面满足摩尔库仑准则。

1.2基本方程

现以锚固端的中心为原点，建立柱面坐标系，并取两者界面上任意一点M（R，θ，z）来进行研究，计算简图见图2。

图2计算简图

Fig.2Calculation model沿锚固体轴线取微端dz，其受力状态如图3所示。

图3锚固段微段的受力图

Fig.3Force diagram on anchorage segment

of recoverable bolt根据微段平衡，可以得出（σz+dσz）A+2πRτzdz=σzA式中：R为锚固体的外半径；σz为锚固体中点M的轴向应力；A为锚固体的有效横截面积。

简化后，有τz=-A2πRdσzdz（1）可以看出，在锚固体受力段内，其边界上任意一点均处于三向受力状态，根据虎克定理，点M（R，θ，z）处的径向应变可以表示为ε′M=1E1[σrR-μ1（σθ+σz）]式中：σθ为锚固体中点M的环向应力；σrR为点M的径向应力；μ1、E1分别为锚固体的泊松比和弹性模量。

令σθ=σr，可得ε′M=1E1[（1-μ1）σrR-μ1σz]（2）同理，在岩土体中M点处的径向应变可表示为ε″M=1E2[σrR-μ2（σ′θ+σ′z）]式中：σ′θ为岩土体中点M的环向应力；μ1、E1分别为岩土体的泊松比和弹性模量。

这里可以认为岩土体在砂浆体的挤压下达到了被动平衡状态，近似认为此时满足朗金土压力理论，则σrR、σ′θ、σ′z三者满足关系式σ′z=σ′θ=σrRtan245°-φ2式（2）可变为ε″M=1E21-2μ2tan245°-φ2σrR（3）根据假设3）可得M点处的变形连续，即满足ε′M+ε″M=0（4）联立式（2）～式（4）可得σrR=μ1E21-2μ2tan245°-φ2E1+（1-μ1）E2σz（5）令k=

μ1E21-2μ2tan245°-φ2E1+（1-μ1）E2，得σrR=kσz（6）另外，根据假设4），锚固体与岩土体界面上的剪应力τz和径向正应力σrR应满足τz=c+σrRtan φ（7）式中：c、φ分别为岩土体的黏聚力和内摩擦角。

联立式（1）、式（6）、式（7）可得σz=De-mz-n（8）式中：D为待定系数；m=2πRA·ktan φ；n=cktan φ。

为了求出待定系数D，根据假设2），在锚固体中任意截面上的正应力均应满足σz=F-∫z02πRτzdzA（9）由式（9）可知，当z=0时，有σz|z=0=FA（10）将式（10）代入式（8）可求出D=FA+n（11）综合上述各式，可得σrR（z）=kFAe-mz+（e-mz-1）nk

τz（z）=FA+ne-mzktan φ （12）

σz（z）=FA+ne-mz-n（13）式（12）即为锚固体与岩土体界面上径向正应力与剪应力的分布规律；式（13）为锚固体中截面上正应力的分布规律，同时，两式也是锚固力传递途径的客观反映。

2对比分析与正确性验证

为了对比验证，选取文献[12]的理论结果与本文结果比较，且采用与其相似的模型，即锚杆拉力F=70 kN，锚固体与岩土体的泊松比均为0.2（μ1=μ2=0.2），内摩擦角为350（可取φ=φ1=35°），无黏聚力，锚固体内、外半径分别为25、75 mm（R=75 mm，A=8πR2/9），E1/E2=6。图4、图5为两种理论结果在此模型上的对比图。

图4锚固段正应力分布曲线

Fig.4Distribution of normal stress along the bonded length图5锚固段剪应力分布曲线

Fig.5Distribution of shear stress along the bonded length从图4、图5可以看出：两种公式计算出的锚固段正应力都在端部达到最大值（4.46 MPa），锚固体受挤压产生的膨胀变形也应该在锚固段正应力最大处出现（即锚固端），相应的，该处也应会产生最大的剪应力，而本文的模型恰好能够满足这一点，这从一个方面证明了本文结论的可靠性。锚固段剪应力从锚固端开始就迅速减小，其减小的速度与图5中剪应力的分布集度大小一致。从图5中可以明显发现，在近锚固端，文献[12]和本文的剪应力分布非常集中，这也是图4中轴向应力下降很快的原因。同时，从图4、图5中还可以看出，锚固段上的应力分布有一个范围，超过这个范围，多余的锚固段不再起作用。

文献[12]中提出，当锚杆从淤泥或淤泥质土中拔出時，剪应力沿全长趋于均匀分布。现可设F=70 kN，锚固体与岩土体的泊松比均为0.45，内摩擦角为150，无黏聚力，锚固体内、外半径分别为25、75 mm（R=75 mm，A=8πR2/9），E1/E2=650。依然按照两种理论得出的剪应力进行比较分析（见图6）。

图6锚固段剪应力分布

Fig.6Distribution of shear stress along the bonded length从图6可以看出，本文推导的计算公式趋于均匀分布，与实际情况更为相符，这也从另一方面验证了该理论的正确性。

3相關参数的影响分析

下面分别改变相关参数来分析相关因素对锚固段上峰值剪应力及剪应力分布范围的影响。

3.1弹模比E1/E2对锚固段剪应力分布的影响

E1/E2为锚固体弹性模量与岩土体的弹性模量之比（简称“弹模比”），如果令锚固体的模量不变，其值越小，表明岩土体越坚硬；反之，岩土体越松软。图7是在不同E1/E2条件下按照本文公式求得的锚固段上剪应力的分布规律。

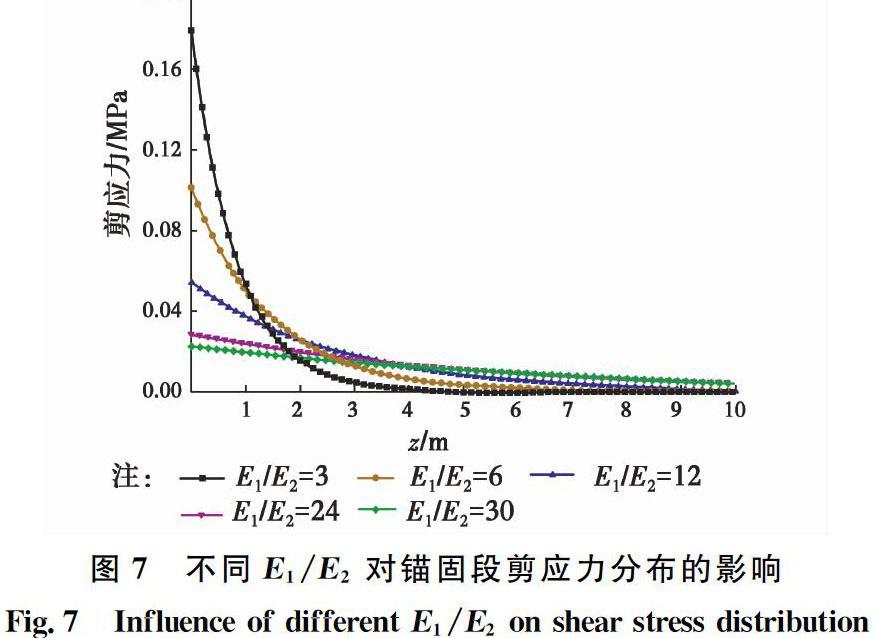
图7不同E1/E2对锚固段剪应力分布的影响

Fig.7Influence of different E1/E2 on shear stress distribution从图7中可以看出，不同岩土条件下的剪应力分布有较大差异，岩土体越松软，剪应力峰越低，分布越均匀，但是，分布范围更大；反之，当岩土体变得坚硬时，剪应力峰值较高，分布范围越来越集中在锚固端附近。因此，弹模比（即E1/E2）对应力分布的影响比较关键。

3.2泊松比μ对锚固段剪应力分布的影响

利用本文推导的公式，分别取不同泊松比并计算出相应条件下剪应力的分布，见图8。

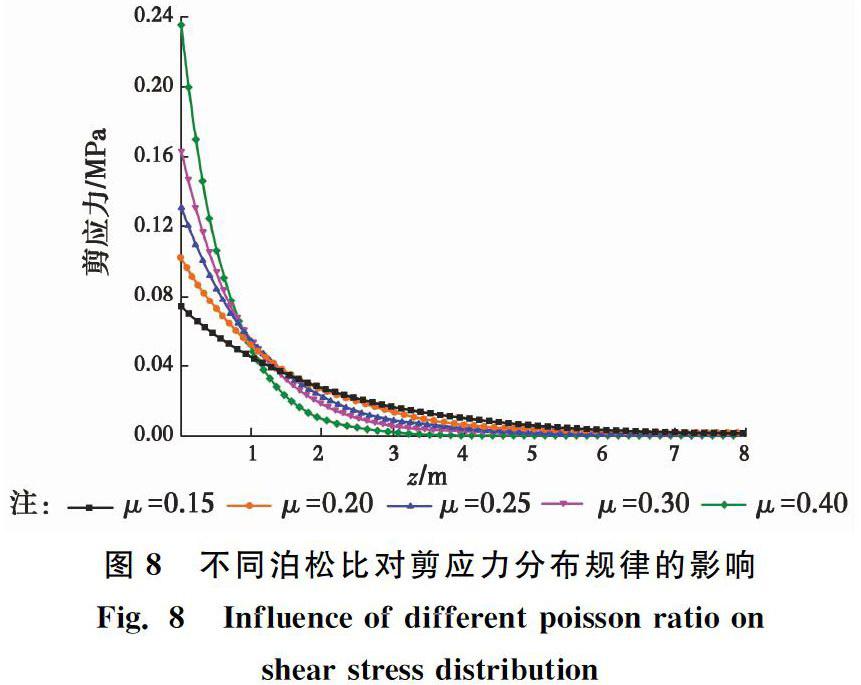
图8不同泊松比对剪应力分布规律的影响

Fig. 8Influence of different poisson ratio on

shear stress distribution从图8中可以看出，泊松比μ越大，剪应力峰值越大，分布越集中，剪应力的分布范围越小；相反，泊松比变大时，剪应力峰值变小，分布越均匀，但是，分布范围变大。可见，岩土体泊松比也是影响应力分布的一个关键因素。

3.3锚固体外半径R对其剪应力分布的影响

保持锚固体内半径25 mm不变，改变其外半径来探讨锚固段剪应力分布的变化。

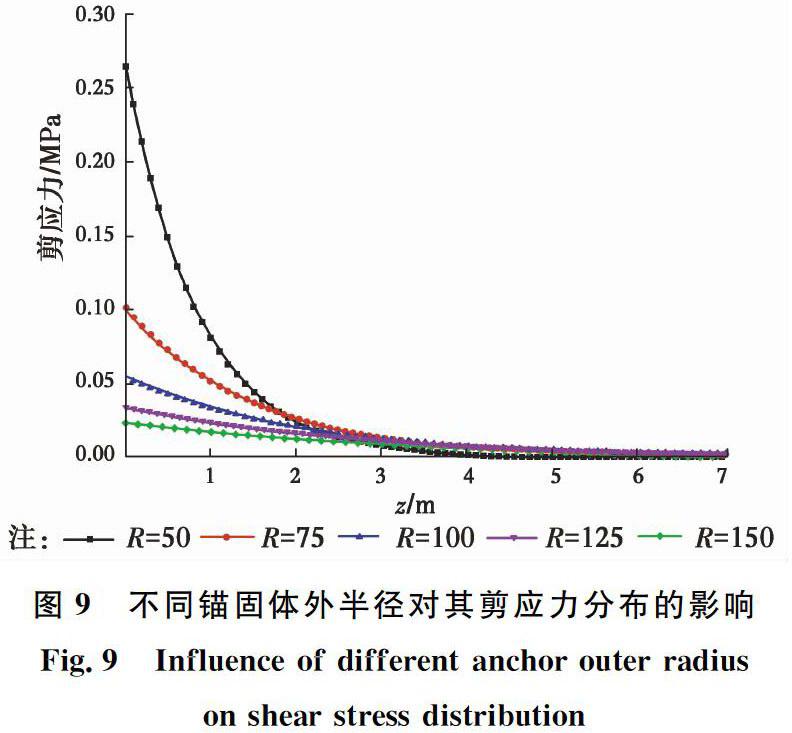
图9不同锚固体外半径对其剪应力分布的影响

Fig.9Influence of different anchor outer radius

on shear stress distribution由于锚固段上的剪应力也会随着锚固体半径的变化而变化，即，如果锚固体半径对锚固端上应力分布范围没有一点影响，其剪应力与正应力也会随着锚固半径的变化而变化，容易造成一种假象。为了弥补这一缺陷，采取“归一化”措施，选取R=75 mm为参照，将任意半径为R的锚固段上的剪应力τ等效为该参照下的剪应力τ0，其计算式为τ0=R75τ图10不同锚固体外半径对其等效剪应力分布的影响

Fig.10Influence of different anchor outer radius

on equivalent shear stress distribution从图9、图10中可以看出，锚固体的半径对其剪应力的分布也有很大影响，半径越大，剪应力分布越均匀，分布范围越大，峰值越小；反之，则相反。

4结论

1） 在特定荷载和特定岩土体参数下，岩土体与砂浆体界面上的应力分布有一个范围，超过这个范围之后，锚固段将不会再起到作用。

2）锚固端处的应力集中比较明显，且在该处的出现了剪应力峰值，同时，锚固段正应力也在该处达到最大，之后两者迅速变小，最终趋近于0。

3）锚杆锚固段上的峰值剪应力及剪应力分布范围受锚固体与岩土体两者弹性模量之比E1/E2、岩土体泊松比μ以及锚固体外半径R三者的影响较大。其中，E1/E2、R越小，μ越大，剪应力峰值应力越大，剪应力分布范围越小；反之，则相反。

参考文献：

[1] ZHANG J H. Selfdrilling type recoverable anchor rod：CN 203475427 U[P]. 2014.

[2] 吴明喜.可回收锚杆[P]. CN104264671A. 2015.

WU M X. Recoverable bolt [P]. CN104264671A. 2015.（in Chinese）

[3] 王清标，吕荣山，孔迎春，等.一种注浆膨胀且部分可回收锚杆[P]. CN204476442U. 2015.

WANG Q B， LYU R H， KONG Y C， et al. A grouting expansion and partially recoverable anchor rod [P]. CN204476442 U. 2015. （in Chinese）

[4] 王国庆，郭猛.可回收锚杆的创新及应用[J].建筑技术， 2013， 44（7）：652654.

WANG G Q，GUO M.Innovation and application of recyclable bolt [J]. Construction Technology，2013，44 （7）： 652654. （in Chinese）

[5] GUO J J. Recoverable resin bolt anchoring section anchoring characteristic study [J]. Coal Engineering， 2009（10）：6567.

[6] LI Z P， HUANG M L， WANG J， et al. Study on the recoverable anchor cable supporting scheme optimization design for metro foundation pit [J]. Chinese Journal of Underground Spaces & Engineering，2012，8（1）：154160.

[7] LI Z P ， LI W T ， WANG J. Study on stress distribution and the bonding length forbonding segment of recoverable anchor cable [J]. Journal of Beijing Jiaotong University， 2011， 35（4）：5761.

[8] ZHANG S， YU S， HUANG Y， et al. The experiment about recoverable anchor cable in the foundation pit support [C]//International Conference on Advanced Design and Manufacturing Engineering，2015.

[9] 范浩，汪洋.新型胀壳式可回收锚杆的研制与应用[J].煤矿机械， 2015， 36（4）：237238.

FAN H，WANG Y.Development and application of new expanded shell recoverable bolt [J].Coal Mine Machinery， 2015， 36 （4）： 237238. （in Chinese）

[10] CHEN Z B， WANG X J， DING W Q. Numerical analysis of mechanical behaviors of largediameter recoverable anchors [J]. Chinese Journal of Geotechnical Engineering， 2012， 34（Sup1）：172176.

[11] 龐有师，刘汉龙，柯结伟.新型可回收锚杆锚固段应力分布规律[J].解放军理工大学学报，2009， 10（5）：461466. （in Chinese）

PANG Y S， LIU H L， KE J W. Stress distribution along bonded length of newtype recoverable anchor [J]. Journal of PLA University of Science & Technology， 2009， 33（3）：257264.

[12] 庞有师，刘汉龙，龚医军.可回收式锚杆抗拔试验研究[J].岩土力学，2010， 31（6）：18131821.

PANG Y S， LIU H L， GONG Y J. Study of pullout tests of recoverable anchors [J]. Rock & Soil Mechanics， 2010， 31（6）：18131821. （in Chinese）

[13] 刘余欣，吴志斌，梅国雄.可回收式锚杆（索）技术的发展现状及展望[C]//全国青年岩土力学与工程会议暨青年华人岩土工程论坛，2013.

LIUS Y， WUZ B， MEIG X. Development and prospect of recoverable bolt （Cable） technology [C]//National Youth Geomechanics and Engineering Conference & Young Chinese Geotechnical Engineering Forum， 2013. （in Chinese）

[14] 刘汉龙，戴会超，庞有师.一种可回收式锚杆[P].中国. 200420080599，200485.

LIU H L， DAI H C， PANG Y S. A kind of recoverable bolt [P]. 200420080599， 200485. （in Chinese）