考虑圆拱效应的桩孔最大自立深度

黄博杰 曹永红 华建民 康明

摘要：对土体稳定性的分析计算大都采用基于二维理论推导出的公式，为解决其无法考虑在空间课题下桩孔圆拱效应的问题，基于别氏理论和挡土墙原理，考虑土体圆拱效应以及孔径对孔壁稳定性的影响，提出计算孔壁自立稳定最大孔深的计算模型；根据别氏公式解并借助MATLAB数值分析软件，对模型中的相关系数进行多次调整，最终提出了简化计算公式，对比分析了计算公式与别氏公式解，结果证明该公式能较好地近似计算别氏理论解，且形式较别氏公式简洁。

关键词：孔壁稳定性；圆拱效应；挡土墙原理；简化模型

中图分类号：TU753.3 文献标志码：A文章编号：16744764（2018）02000606

收稿日期：20170330

作者简介：黄博杰（1991 ），男，主要从事工程建造研究，Email：hbj5879@163.com.

曹永红（通信作者），女，副教授，博士，Email：505626346@qq.com.

Received：20170330

Author brief：Huang Bojie （1991 ）， main research interest： engineering construction， Email： hbj5879@163.com.

Cao Yonghong （corresponding author）， associate professor， PhD， Email： 505626346@qq.com.Research of the maximum self supporting depth of pile hole

considering the effect of circular arch

Huang Bojie， Cao Yonghong， Hua Jianming， Kang Ming

（School of Civil Engineering， Chongqing University， Chongqing 400045， P. R. China）

Abstract：Most of the analysis and calculation of soil stability is based on the formula from the twodimensional theory， in order to solve the problem that it cannot take into account the effect of the pile hole circular arch in the space project Based on В. Г. theory and the principle of retaining wall， considering the soil arch effect on the stability of the hole wall， a calculation model for calculating the maximum hole depth of selfsupporting hole wall was put forward. According to different formula solutions and the MATLAB numerical analysis software， the correlation coefficient in the model was adjusted several times. Finally a simplified calculation formula was proposed， the calculation formula and В. Г. formula solution were contrasted and analyzed. The result shows that this formula can calculate В. Г. theoretical solution for better approximation， which is more concise than the В. Г. formula， beneficial to the popularization and application， and more convenient for application in practical engineering.

Keywords：borehole stability； circular arch effect； principle of retaining wall； computational model

鉆孔灌注桩以其地层适应能力强、节约钢材、施工振动噪音小、无需接桩和截桩、对地层扰动小、承载力高等优点而被大量应用于工程项目中[1]，这使得钻孔灌注桩施工技术可以不通过新钻具和新工艺的结合，而用旋挖钻进工艺与全套管跟管钻进、全套管护壁钻进等特殊工法和特殊钻具配套的施工方法，解决了全套管钻进的成本问题，推动了钻孔灌注桩施工技术的发展[23]。该施工方法通常需要先预钻孔至一定深度，再下放套管跟进护壁。预钻孔深度影响工程的进度和成本，预钻孔深度越大，套管一次性下放深度越大，施工速度越快，施工成本随之降低，但发生塌孔事故的风险也越大。预钻孔的深度主要与孔壁的稳定性有关，因此，研究桩孔的稳定性对工程施工具有重要意义。

针对孔壁稳定性的研究表明，影响孔壁稳定性的因素包括土体性质、孔深、孔半径等 [47]。近年来，有关桩孔稳定性的研究主要针对有泥浆护壁的情况，而针对桩孔自立深度的研究较少。Westergard[8]基于莫尔库伦强度准则，进行了孔壁稳定性研究。Aadony等[9]考虑岩石的各向异性，得到了孔壁稳定性分析模型的半解析解。龚辉等[10]、徐栓强等[11]基于双向受压无限板孔理论（将土体看作弹性体）计算孔壁应力大小，利用统一强度理论考虑中间主应力的影响，分别给出了桩孔和圆形竖井极限深度。李林等[12]基于SMP准则改进的修正剑桥模型对饱和黏土中钻孔灌注桩孔壁稳定性进行了研究。李小青等[13]基于挡土墙理论，对干成孔孔壁稳定性进行分析，给出的孔壁自立稳定最大深度公式与边坡不能承受拉力时非线性准则上限分析解一致。曾二贤等[14]基于挡土墙理论，对干成孔孔壁稳定性进行分析，给出的孔壁自立稳定的最大深度公式与边坡能承受拉力时非线性准则上限分析解一致。

第2期 黄博杰，等：考虑圆拱效应的桩孔最大自立深度上述研究大都没有考虑土体圆拱效应对土体稳定性的有利影响，简单地基于挡土墙理论或弹性理论提出近似计算方法，作为人工挖孔桩的施工依据还可接受，但作为机械施工的指导依据则显得过于保守。笔者依据别列札恩采夫提出的松散体极限平衡的轴向对称理论（简称别氏理论）[15]，考虑土体的圆拱效应，并结合挡土墙计算原理，提出一个计算桩孔自立深度的别氏理论简化模型，结果证明，该公式能很好地满足别氏公式，并且形式较别氏公式简洁，更易应用于工程实践。

1别氏理论与挡土墙理论的对比

别列札恩采夫 [15]基于土体极限平衡理论，发展了空间课题第1种情况的理论，即，对称于轴线的应力状态的极限平衡问题（轴向对称问题）。该理论的土体破坏准则实际上就是MohrCoulomb准则，认为土壤平衡状态的破坏是某一部分土体对另一固定部分土体取移动形式，从微观角度来理解，则是认为土体处于极限平衡状态时，某一微面积上土体受剪切应力的绝对值等于其本身的粘结力加上外荷载重和自重所产生的摩擦力。即|τ|=c+σtan φ式中：|τ|为剪切应力的绝对值；c为土体的粘着力；φ为土体的内摩擦角；σ为作用在滑动面的的正应力。

由此不难看出，别氏理论和挡土墙理论在本质上是一样的，只是别氏理论是对空间课题的研究，将桩孔看作一个空心圆柱体的构筑物而并非一堵墙，滑动面是一个环状空心圆锥面而非平面，考虑了土层向桩孔中心作位移时，其本身相互挤压作用对土体稳定的有利作用；而挡土墙理论则是对平面课题的研究，不能考虑土体间的相互挤压，因而无法考虑桩孔半径对孔壁稳定的影响[16]。

1.1别氏理论研究的内容

别列札恩采夫在其著作中除了论述空间课题的极限平衡条件、组成微分方程式和制定该方程式的一般解法外，还推导出具有实际应用价值的简化计算方法，主要包括圆形压块的极限压力（圆形地基承载力）、按照环形面积分布的极限压力以及筒形地坑墙上的极限压力[15]。专门针对桩孔稳定性的研究虽然没有提及，但可以借鉴挡土墙理论，依据墙后主动土压力的计算方法推导竖直边坡稳定临界高度，根据作用在筒形地坑护壁上的别氏理论主动土压力计算公式推导桩孔最大自立深度。

1.2别氏理论和挡土墙理论公式

别氏理论对“松散体”概念的定义与挡土墙理论相同，对于土体极限平衡的条件、极限平衡微分方程的求解，别氏理论是将B.B.索科洛夫斯基在解决挡土墙平面问题时所用的方法，用于轴对称空间问题的求解，方法一致[17]。

笔者不再重复理论推导，直接给出别氏护壁主动土压力计算式[15]。 PB=γR0tan（45°-φ/2）λ-11-R0Rbλ-1+

qR0Rbλtan2（45°-φ/2）-ccotφ·

R0Rbλtan2（45°-φ/2）-1（1）挡土墙主动土压力计算式为[16] PD=γHtan2（45°-φ/2）+q·

tan2（45°-φ/2）-2ctan（45°-φ/2）（2）式中：PB为土体作用于护壁上的主动土压力，kPa；PD为土体作用于挡土墙上的主动土压力，kPa；γ为土容重，kN/m3；φ为土体的内摩擦角，°；c为土体粘聚力，kPa；H为计算截面距离地表的深度，m；q为地表的均布荷载，kN/m2；R0为桩孔掘进半径，m；Rb为土体滑动线与地面交点的横坐标值，m，Rb=R0+Htan（45°-φ/2）；λ为简化系数，λ=2tanφtan（45°-φ/2）。

当地表没有均布荷载或均布荷重很小，式（2）即為PD=γHtan2（45°-φ/2）-2ctan（45°-φ/2）（3）当PD≤0时，说明土体处于稳定状态，无需支护，可得竖直边坡的临界高度为HD=2cγtan（45°-φ/2）（4）同理，可令PB=0，根据式（5）求桩孔最大自立深度。γR0tan（45°-φ/2）λ-11-R0Rbλ-1=

ccotφ1-R0Rbλtan2（45°-φ/2）（5）近年来，别氏理论一直未能被真正应用于实践[18]，主要原因包括[17]：1）公式应用者未认清该理论的实质，片面地认为根据该公式能够得到一个普遍结论：在表层土的一定深度下，地压随着深度增加不变；2）推荐者往往把这个理论和挡土墙理论绝对地对立起来，看不到在一定条件下这两个理论会引出近似的结果；3）该理论的公式形式过于复杂，给计算带来很大不便，推荐者通常将其作为一个理论流派进行简单介绍，没有对其进行深入分析，极大影响了在实际工程中的应用。

对于空间轴对称问题，别氏理论解释的现象比挡土墙公式更接近于实际，应将其应用于实际计算中。因此，对别氏理论深入分析，提出一个近似求解别氏理论的简化计算式很有必要。

2简化计算模型

2.1别氏理论解分析

根据别氏理论公式（5），最大自立深度是一个隐式解，而非显式解，形式比较复杂，对于该方法的应用造成了困难，笔者利用数值计算二分法计算出部分不同直径、不同土质下的桩孔最大自立深度（如表1所示）。

由表1可知，对于同一土质而言，桩孔半径R0越大，别氏理论所求得的桩孔最大自立深度HB越小，但是R0与HB并不成严格的反比例关系；在同一桩径下，土质越好，HB/HD越大，说明影响桩孔圆拱效应的除了桩孔半径R0外，还有土体的粘聚力c和内摩擦角φ，但粘聚力c和内摩擦角φ与HB/HD并不成严格的正比例关系；还可以发现，当R0→∞时，HBHD→1，此时别氏理论解与挡土墙理论解相一致，当掘进半径R0→∞时，问题则变成了平面课题，理所应当与挡土墙理论符合，这也证明了别氏理论的合理性。表1别氏理论与挡土墙理论计算值对比

Table 1 Comparison of the theoretical value of the theory of

retaining wall and В. Г.序号γ/

（kN·m-3）c/

kPaφ/

（°）R0/

mHB/

mHD/

mHBHD1181080.63.563 1.278 2.788 21810812.732 1.278 2.137 3181081.52.250 1.278 1.760 4181081001.291 1.278 1.010518.510150.63.845 1.409 2.729 618.5101512.865 1.409 2.034 718.510151.52.356 1.409 1.672 818.510151001.421 1.409 1.009 91910180.63.882 1.449 2.679 1019101812.867 1.449 1.979 111910181.52.361 1.449 1.630 121910181001.460 1.449 1.008 1318.520150.612.074 2.818 4.285 1418.5201518.622 2.818 3.060 1518.520151.56.726 2.818 2.387 1618.520151002.866 2.818 1.017 171920180.612.666 2.898 4.371 1819201818.765 2.898 3.025 191920181.56.752 2.898 2.330 201920181002.944 2.898 1.016 2119.520200.612.873 2.930 4.394 2219.5202018.735 2.930 2.982 2319.520201.56.683 2.930 2.281 2419.520201002.974 2.930 1.015 2519.550180.662.802 7.058 8.898 2619.55018141.414 7.058 5.867 2719.550181.530.255 7.058 4.286 2819.550181007.339 7.058 1.040 292050200.668.091 7.141 9.536 30205020143.112 7.141 6.037 312050201.530.745 7.141 4.306 322050201007.411 7.141 1.038 3320.550230.678.982 7.370 10.717 3420.55023146.862 7.370 6.359 3520.550231.532.193 7.370 4.368 3620.550231007.632 7.370 1.036 注：HB為利用二分法计算出的别氏理论桩孔最大自立深度，m。2.2简化公式的提出

根据以上分析结果，提出一个近似求解桩孔最大自立稳定深度的简化计算模型。Hmax=a·c+b·φ+mR0+1·HD（6）式中：a、b、m为待定系数。

利用MATLAB数值分析软件，跟据表1中的数据运用非线性回归法初步确定了模型（6）中的待定系数a、b、m，按照在保证足够精确的条件下公式相对别氏公式趋于保守的原则对系数进行一定调整，并与更多数据进行对比验证，最终提出桩孔最大自立稳定深度计算简化式，见式（7）。Hmax=k·0.9c+0.1φ10R0+1·2cγtan（45°-φ/2）（7）式中：Hmax为桩孔最大自立稳定深度；k为一个与土质有关的系数，粘土取1.0，亚粘土取0.9，亚砂土取0.8。

需要指出的是，式（7）中0.9c+0.1φ10R0只表示一个与土体的粘聚力c、内摩擦角φ和桩孔半径R0有关的系数，无量纲；其中c为粘聚力以kPa为单位时的取值，φ为内摩擦角以度（°）为单位时的取值，R0为以m为单位时的取值。

当土层上部有均布荷载q时，将均布荷载转化为土体厚度HQ=qγ，利用Hmax-HQ来近似计算土层上部有均布荷载时桩孔最大自立稳定深度。

由别氏理论推导过程可知，式（7）只适用于土体顶部桩周Rb范围内无荷载、有可忽略的荷载或者有沿桩孔径向均布荷载的情况；距桩轴线一侧Rb范围内有不可忽略的荷载时，可利用挡土墙理论公式近似计算，计算结果相对偏于安全。

3公式分析与对比

3.1简化公式的分析

由简化公式（7）不难看出，该式能够直观地反映各土体性质对桩孔最大自立稳定深度Hmax的影响。桩孔最大自立稳定深度Hmax与土体重度γ成反比关系，这与直观认识相符；随着土体粘聚力c和内摩擦φ的增大，Hmax也随之增大，但不成严格的正比例关系，并且土体粘聚力c的影响远大于内摩擦φ值得影响，这与别氏理论解体现出的规律类似；对于砂性土，粘聚力c=0，其最大自立稳定深度Hmax恒等于0，这也说明，砂性土孔壁总不稳定，在没有任何护壁措施下，干成孔无法进行，这与沙土坡稳定性分析结论也一致；再者，无论土体粘聚力c和内摩擦φ取值如何，当土体掘进半径R0→∞时，Hmax→HD，这也体现了简化公式的合理性；将与土质类别有关的系数k转化为k·0.9c+0.1φ10R0的分母，粘土为0.9c+0.1φ10R0，亚粘土为0.9c+0.1φ11.1R0，亚砂土为0.9c+0.1φ12.5R0。因此，系数k可理解为掘进半径R0对不同类别土质的最大自立稳定深度的影响不同，这与王云岗等[19]对钻孔灌注桩孔壁稳定性的结论一致。

根据以上分析，从定性的角度来看，提出的简化公式（7）是合理的。

3.2简化公式与别氏公式的对比

对同一种土质而言，通常φ值也会随着c的增大而增大，根据别列札恩采夫对土体粘聚力和内摩擦的理解，土体粘聚力和内摩擦角是土体的力学特征，不能看作是土体抗剪强度的独立形式，因此，通过在其他参数一定的前提下研究c值或φ值单独的变化来判断公式的实用性没有多大意义。笔者根据朱松耆[17]推荐的粘土类土计算数值（见表2）对简化公式和别氏公式进行比较。

表2粘土类土的计算数值

Table 2The calculated values of clayey soil序号稠度状态B粘土γφc亚粘土γφc亚砂土γφc1固态<021.50 22 100 21.60 256020.50 28202半固态0～0.2521.00 20 60 21.00 234020.00 26153坚塑性0.25～0.5020.50 18 40 20.00 212519.50 24104软塑性0.50～0.7519.50 14 20 19.00 171519.00 2055流塑性0.75～1.0019.00 8 10 18.50 131018.50 1826流性>1.0018.00 6 5 18.00 10518.00 140注：γ为土的容重，kN/m3；φ为内摩擦角，°；c为粘聚力，kPa。分别对粘土、亚粘土和亚砂土在不同力学参数下不同孔径的HBHmax值（共153组数据）进行分析（如图1～图3所示），以对比简化公式与别氏理论解的相似程度。

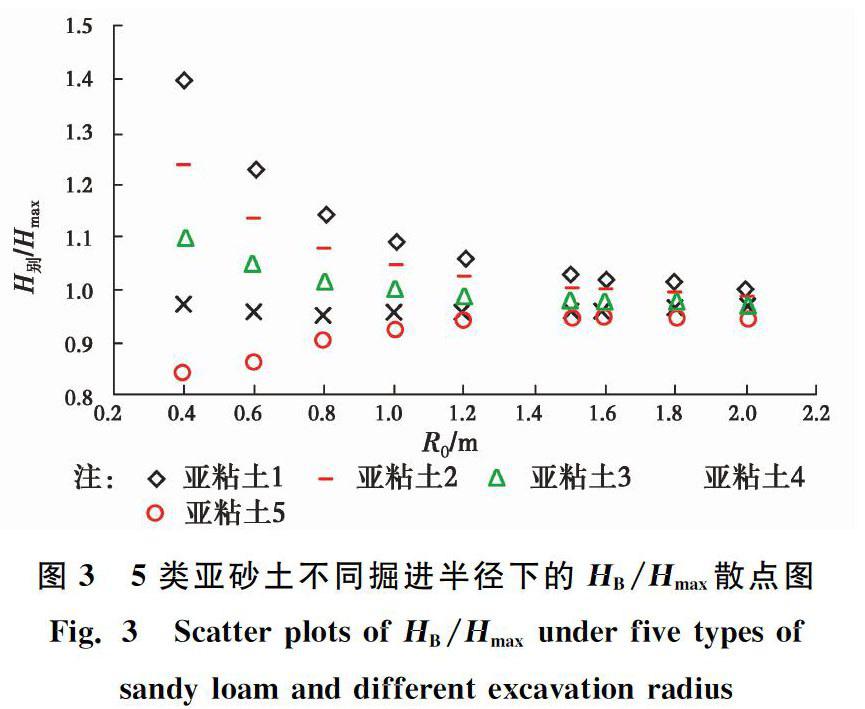
图16类粘土不同掘进半径下的HB/Hmax散点图

Fig. 1Scatter plots of HB/Hmax under six types of

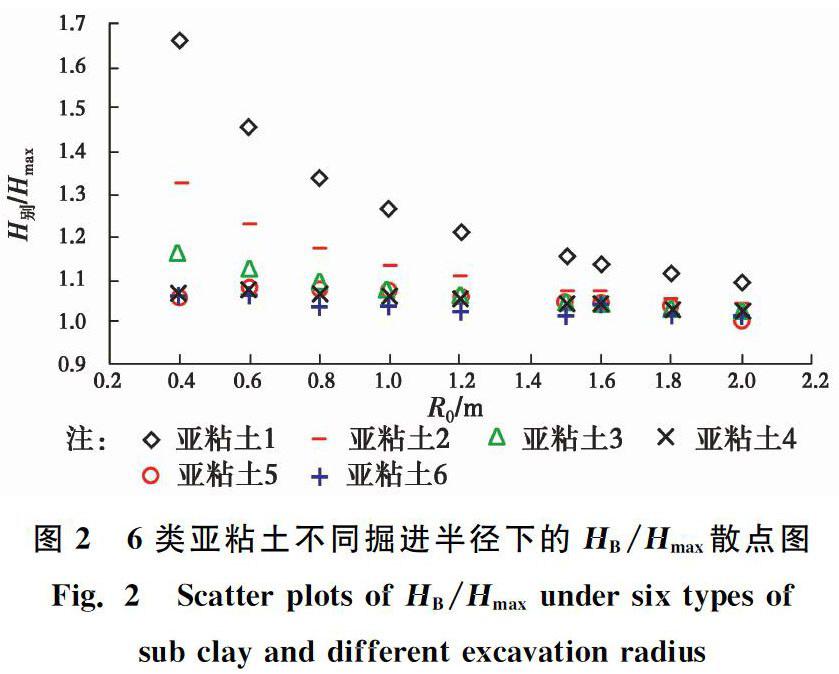
clay and different excavation radius图26类亚粘土不同掘进半径下的HB/Hmax散点图

Fig. 2Scatter plots of HB/Hmax under six types of

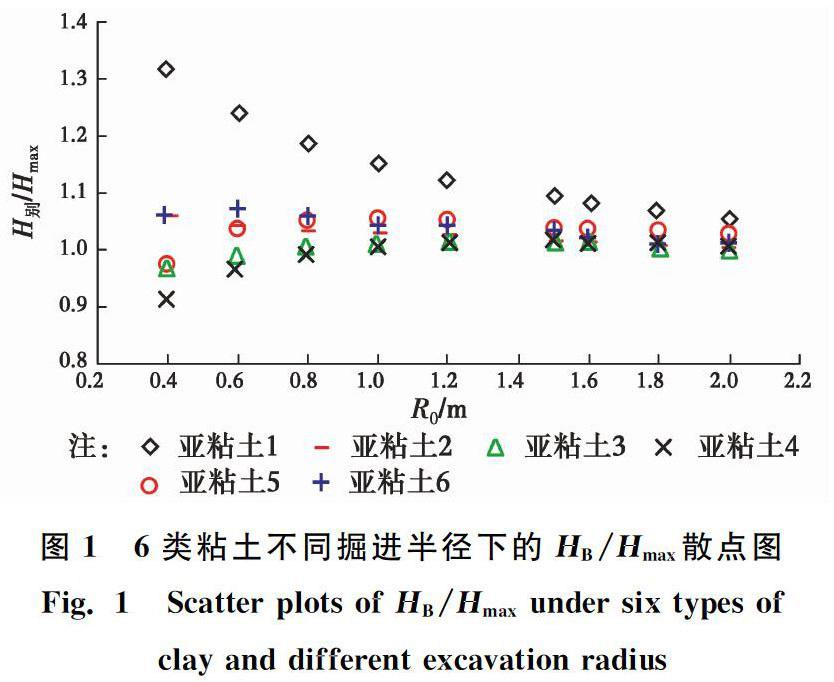
sub clay and different excavation radius图35类亚砂土不同掘进半径下的HB/Hmax散点图

Fig. 3Scatter plots of HB/Hmax under five types of

sandy loam and different excavation radius由图1可知，在这54个数据中，只有粘土1在R0≤1.2 m时的5个数据采用简化公式计算的误差超过10%，即超过90%的数据利用简化公式计算误差在10%以内，说明简化公式能够较好地近似计算别氏理论解。

由图2可知，所有计算值均满足Hmax≤HB，超过90%的数据利用简化公式计算误差在20%以内，说明简化公式在计算亚粘土自立深度时能够在更保守的前提下较好地近似计算别氏理论解。

由图3可知，超过95%的数据利用简化公式计算误差在20%以内，近85%的数据计算误差在10%以内，说明简化公式在计算亚砂土自立深度時能够较好地近似计算别氏理论解。

图1、图2、图3都呈现出相同的规律：随着土体掘进半径的增大，简化公式解与别氏理论解越接近；土质越好，简化公式解相对越保守，考虑到土质越好，HB越大，Rb也越大（几十甚至上百米），在实际工程中很难保证在孔径Rb范围内都无不可忽略的荷载，因此，利用简化公式更为保守，更为合理。至于少部分Hmax>HB的情况，均出现在桩孔最大自立深度不大的情况，在实际应用中考虑安全系数完全能够保证实用性。

综上所述，简化式（7）能够在偏保守的条件下较为精确地近似代替别氏理论在各类粘土类土及常用孔径下的孔壁最大自立深度解，从定性和定量的角度来看都是合理的。

4结论

1）别氏理论解考虑了土层向桩孔中心作位移时其本身相互挤压作用，能够考虑土体挖掘半径（即圆拱效应）的影响，一定条件下（如R0→∞）别氏理论和挡土墙理论会引出近似的结果。对于空间轴对称问题，别氏理论解释的现象比挡土墙公式更接近于实际，应将其应用于实际计算中。

2）通过对别氏理论解的分析，针对别氏理论公式形式复杂，工程应用困难的问题，提出了计算桩孔最大自立深度的简化计算公式。

3）根据别氏理论与简化公式的对比分析发现，简化公式近似计算别氏理论解可行、有效、优势明显。为别氏理论在实际工程中的应用提供了新思路和方法。

参考文献：

[1] 肖勇杰，许万强，陈福全. 全套管大直径振动取土灌注桩施工新技术[J].施工技术，2015， 44（1）： 6164.

XIAO Y J， XU W Q， CHEN F Q. A new construction technology of large diameter castinplace piles with sleeves driven by vibratory hammers [J]. Construction Technology， 2015， 44（1）： 6164. （in Chinese）

[2] 刘家荣. 无循环钻进工艺在易坍塌、缩孔和卵砾石地层的应用[J].地质与勘探，2010， 46（5）：960966.

LIU J R. Application of nocirculation drilling technology to collapse prone， shrinkable and gravel strata [J]. Geology and Exploration， 2010， 46（5）： 960966. （in Chinese）

[3] LONG Z Y， GUI L G. Current situation and development for China's 1000 m deep shaft sinking [J]. Tunnels & Tunnelling International， 2012，69（6）：7274.

[4] 崔强，何西伟，曹丹京，等. 输电线路掏挖基础机械成孔过程中孔壁土体稳定性分析[J]. 冰川冻土，2016， 38（4）： 922928.

CUI Q， HE X W， CAO D J， et al. Stability analysis of borehole wall of digged foundation of transmission line during mechanized drilling [J]. Journal of Glaciology and Geocryology， 2016， 38（4）： 922928. （in Chinese）

[5] ZHI D D， YA P D， PEI W Y. Influencing factors analysis of stability of hole wall of bored pile in seasonal frozen ground in the west of China [J]. Applied Mechanics and Materials， 2013， 256259： 441444.

[6] JAMSHIDI E， AMANI M. Numerical wellbore stability analysis using discrete element models [J]. Petroleum Science and Technology， 2014， 32（8）： 974982.

[7] 王中文. 钻孔灌注桩孔壁稳定性的影响因素研究[J]. 公路交通科技， 2011， 28（1）： 8690.

WANG Z W. Research of factors affecting stabilization of hole wall of bored pile [J]. Journal of Highway and Transportation Research and Development， 2011， 28（1）： 8690. （in Chinese）

[8] WESTERGARD H M. Plastic state of stress around a deep well [J]. Boston Society of Civil Engineers， 1940， 27： 15.

[9] AADNOY B S， CHENEVERT M E. Stability of highly inclined boreholes [J]. SPE Drilling Engineering， 1987， 2（4）： 364374.

[10] 龚辉，赵春风. 基于统一强度理论桩孔稳定性分析[J].沈阳建筑大学学报（自然科学版），2011， 27（2）： 237241.

GONG H， ZHAO C F. Stability analysis of borehole based on unified strength theory [J]. Journal of Shenyang Jianzhu University （Natural Science）， 2011， 27（2）： 237241. （in Chinese）

[11] 徐栓强，侯卫. 考虑岩体中间主应力效应的竖井稳定性分析[J].地下空间与工程学报，2007， 3（6）： 11681170.

XU S Q， HOU W. Analysis on stability of a shaft with considering the effect of intermediate principal stress of rock mass [J].Chinese Journal of Underground Space and Engineering， 2007， 3（6）： 11681170. （in Chinese）

[12] 李林，李镜培，岳著文，等. 饱和黏土中钻孔灌注桩孔壁稳定性力学机制研究[J]. 岩土力学，2016， 37（9）： 24962504.

LI L， LI J P， YUE Z W， et al. Mechanical mechanism of holewall stability of bored pile in saturated clay [J]. Rock and Soil Mechanics， 2016， 37（9）： 24962504. （in Chinese）

[13] 李小青，乌效鸣. 钻孔灌注桩孔壁稳定性分析[J].地质与勘探，2001， 37（2）： 7476.

LI X Q， WU X M. Discussed and analyzed the stability of wall of bored pile [J]. Geology and Exploration， 2001， 37（2）： 7476. （in Chinese）

[14] 曾二贤，冯衡，胡星，等. 输电线路掏挖基础的孔壁稳定性分析及判别[J].电力建设，2010， 31（8）： 1720.

ZENG E X， FENG H， HU X， et al. Stability analysis on the undercut foundation walls for transmission towers [J]. Electric Power Construction， 2010， 31（8）： 1720. （in Chinese）

[15] В·Г· 别列札恩采夫. 松散体（土壤） 极限平衡的轴向对称问题[M].谢宗梁，黄贻吉，译.北京：建筑工程部出版社，1956.

В. Г. Березанцев. Axial symmetry problem of limit equilibrium of loose soil [M]. XIE Z L， HUANG Y J， Translated. Beijing： Construction Engineering Press， 1956. （in Chinese）

[16] 李广信，张丙印，于玉贞. 土力学[M]. 2版. 北京：清华大学出版社，2013.

LI G X， ZHANG B Y， YU Y Z. Soil Mechanics [M]. Second Edition. Beijing： Tsinghua University Press， 2013. （in Chinese）

[17] 朱松耆. 表土層中圆形竖井地压的计算[J].有色金属（采矿部分），1974（5）： 1319.

ZHU S Q. The calculation of circular vertical shaft earth pressure of surface soil layer [J]. Nonferrous Metals （Mining Section）， 1974（5）： 1319. （in Chinese）

[18] 崔广心. 深厚表土中竖井井壁的外载[J].岩土工程学报，2003， 25（3）： 294298.

CUI G X. Loading of shaft lining for deep alluvium [J]. Chinese Journal of Geotechnical Engineering， 2003， 25（3）： 294298. （in Chinese）

[19] 王云岗，章光，胡琦. 钻孔灌注桩孔壁稳定性分析[J]. 岩石力学与工程学报，2011， 30（Sup1）： 32813287.

WANG Y G， ZHANG G， HU Q. Analysis of stability of bored pile holewall [J]. Chinese Journal of Rock Mechanics and Engineering， 2011， 30（Sup1）： 32813287. （in Chinese）