地质雷达信号分析的双正交小波预测反褶积法

凌同华 刘浩然 谷淡平 张亮

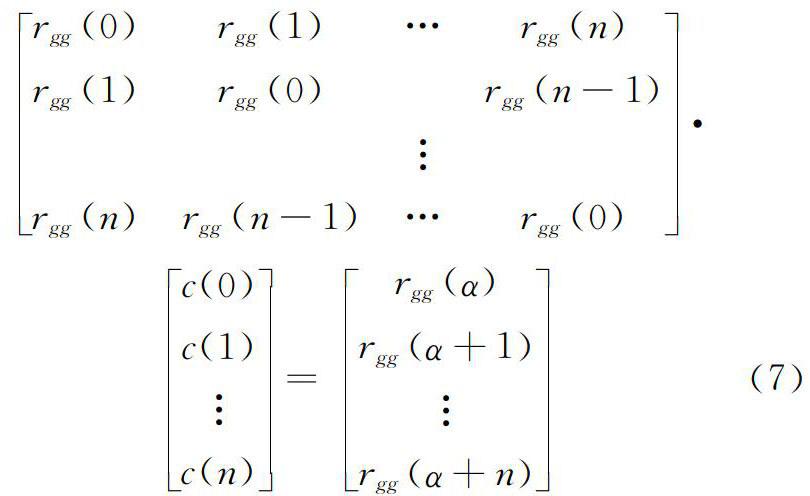
摘要：為了降低电磁波衰减、噪声干扰等因素对地质雷达检测效果的影响，提出一种双正交小波预测反褶积法（PDBW法）。在PDBW法中，针对地质雷达检测信号选取具有最小重构误差的双正交小波基，运用该小波基将地质雷达检测信号分解成不同频段的时域子信号，对各频段的时域子信号进行预测反褶积等滤波处理，再对处理后的子信号进行重构变换，得到PDBW法的处理结果。将PDBW法用于实验检测信号处理，并将处理结果与预测反褶积法的处理结果进行比较，结果表明：PDBW法能有效压制多次回波干扰，准确识别深部信号，显著提高深部信号信噪比，从而进一步改善了地质雷达探测分辨率和图像分析的准确性。

关键词：地质雷达；双正交小波分析；预测反褶积；探测分辨率；信噪比

中图分类号：TN959.71 文献标志码：A文章编号：16744764（2018）02002606

收稿日期：20170615

基金项目：国家自然科学基金 （51678071、51278071）；长沙理工大学桥梁工程领域开放基金（14KC06）；长沙理工大学研究生科研创新项目（CX2015BS02）

作者简介：凌同华（1968），男，教授，博士生导师，主要从事隧道与地下工程研究，Email：lingtonghua@163.com。

Received：20170615

Foundation item：National Natural Science Foundation of China （No. 51678071， 51278071）； Open Fund of Bridge Engineering of Changsha University of Science and Technology （No. 14KC06）； Graduate Research and Innovation Project of Changsha University of Science and Technology （No. CX2015BS02）

Author brief：Ling Tonghua （1968）， professor， doctoral supervisor， main research interests： tunnel and underground engineering， Email：lingtonghua@163.com.A predictive deconvolution method based on biorthogonal

wavelet of GPR signal analysis

Ling Tonghua， Liu Haoran， Gu Danping， Zhang Liang

（School of Civil Engineering and Architecture， Changsha University of Science & Technology， Changsha 410114， P. R. China）

Abstract：In order to reduce the influence of some factors such as the electromagnetic wave attenuation and noise jamming on detection effect of GPR， a predictive deconvolution method based on biorthogonal wavelet was proposed （short for PDBW method）. In the PDBW method， the biorthogonal wavelet basis with the minimum reconstruction error for detection signal of GPR was chosen， using this wavelet to decompose the GPR signals into different frequency band subsignals， and then predictive deconvolution and other filter method were used to deal with each frequency band subsignal in time domain， at last the results of PDBW method by reconstructing each subsignal were get. Using the PDBW method to deal with the detection signal of experiment， the results show that， comparing with the predictive deconvolution， the PDBW method can restrain the multiple echo interference， identify the deep signal precisely， and enhance the signal to noise ratio of deep signal， thus improving the detecting resolution and the accuracy of image analysis of GPR signal.

Keywords：ground penetrating radar；biorthogonal wavelet analysis；predictive deconvolution；detecting resolution；signal to noise ratio

地质雷达具有无损、分辨率高、操作便捷等优点[12]，被广泛用于隧道超前预报、地下管网探测、工程结构检测等众多领域[35]。在检测过程中，高频电磁波的衰减、多次回波的干扰及检测目标尺寸等因素均会影响地质雷达信号的探测分辨率和图像的最终解释效果。

目前，提高雷达探测分辨率的主要方法有：预测反褶积、基于模糊分析的脉冲反褶积、基于最大峰度法的时变反褶积和地层频谱校正等，通过压缩雷达子波和压制多次回波等方式，上述方法能有效改善地质雷达信号的处理效果[611]。然而，当深部信号的信噪比受多次回波干扰而降低时，以上方法很难在压缩子波和抑制回波干擾的同时提高深部信号的信噪比，甚至会导致深部信号丢失并造成错误的图像解释。由于小波分析能够将信号分解成不同频段的时域子信号，在含反射波信息的子信号中，噪声的频段和幅值能量能得到有效控制。因此，对该子信号进行预测反褶积处理便可得到深部信号的反射系数，从而，在抑制多次回波的同时提高深部信号信噪比。

本文以此为切入点，提出一种双正交小波预测反褶积法。该法针对地质雷达信号选取具有最小重构误差的双正交小波基，运用该小波基对地质雷达检测信号进行不同频段的分解和重构，并对各频段的时域子信号进行预测反褶积等滤波处理，再对处理后的子信号进行重构变换，从而得出该法的处理结果。与预测反褶积法相比，该法能有效压制多次回波，准确识别深部信号，显著提高深部信号信噪比，从而进一步提高地质雷达的探测分辨率和图像分析的准确性。

第2期 凌同华，等：地质雷达信号分析的双正交小波预测反褶积法1基本原理

1.1双正交小波的分解与重构

令f∈L2（R），φj，k、φj，k分别为j层的分解尺度函数和分解小波函数，对信号f（t）进行双正交小波分解，信号f（t）的小波分解系数为[12]aj，k=[f，φj，k]

dj，k=[f，φj，k]（1）式中：aj，k、dj，k分别为j层小波分解的近似系数和细节系数。

式（1）中aj，k、dj，k应满足aj+1，k=[aj，k，φj+1，k]

dj+1，k=[aj，k，φj+1，k] （2）令j，k、j，k分别为j层的重构尺度函数和重构小波函数，则双正交小波分析中的重构公式为[13]aj，k=[aj+1，k，j+1，k]+[dj+1，k，j+1，k]（3）1.2预测反褶积法

令预测滤波因子为c（t），时间延迟为n，预测步长为α，地质雷达信号的过去值为f（t-1），f（t-2），…，f（t-n），现在值为f（t），t+α时刻的实际将来值为f（t+α）。

运用反褶积求取t+α时刻的预测值为（t+α）=c（t）g（t）=∑nτ=0c（τ）g（t-τ） （4）预测误差为ε（t+α）=f（t+α）-（t+α） （5）在最小平方反滤波理论中，当误差的平方和取最小值时，预测值接近实际值，则式（5）可改写成c（s）[∑n+αt=0ε2（t+α）]=0 （6）按照Toeplitz矩阵，滤波因子c（t）的求解形式为[14]rgg（0）rgg（1）…rgg（n）

rgg（1）rgg（0）rgg（n-1）

rgg（n）rgg（n-1）…rgg（0）·

c（0）

c（1）

c（n）=rgg（α）

rgg（α+1）

rgg（α+n）（7）将解出的c（t）代入式（5）后，再取Z变换，可得E（z）=F（z）A（z）（8）其中A（z）=1-z-αc（z）（9）在式（8）、式（9）中，z-αE（z）、F（z）、c（z）分别为预测误差ε（t+α）、f（t）和c（t）的Z变换。对A（z）做逆Z变换，可得预测误差滤波因子a（t）=[1，0，0，…，0，-c（1），…，-c（n）]（10）运用a（t）对地质雷达原始数据进行反褶积，得到信号的反射系数序列，即预测反褶积法的计算结果。

2双正交小波预测反褶积法

2.1双正交小波预测反褶积法的基本原理

根据双正交小波的分解重构变换和预测反褶积法，提出了一种改进的反褶积法，即双正交小波预测反褶积法（predictive deconvolution based biorthogonal wavelet analysis，简称PDBW法）。该方法的基本原理如下：

根据式（1）、式（2），对信号f（t）进行j层小波分解，得到如下小波分解系数为d1，k=[f，φ1，k]

d2，k=[a1，k，φ2，k]

dj，k=[aj-1，k，φj，k]

aj，k=[aj-1，k，φj，k] （11）在式（11）中，运用式（3）分别对各层系数进行小波重构，可得式（12）[13]。fd1，k=[d1，k，1，k]

fd2，k=[[d2，k，2，k]，1，k]

fdj，k=[[[dj，k，j，k]，j-1，k]…，1，k]

faj，k=[[[aj，k，j，k]，j-1，k]…，1，k]（12）式中：fdj，k、faj，k分别为第j层系数重构的时域子信号。

按照式（4）～式（10），对各时域子信号进行预测反褶积，得到式（13）所示反射系数序列。ξd1（t）=[ad1（k），fd1（t-k）]

ξd2（t）=[ad2（k），fd2（t-k）]

ξdj（t）=[adj（k），fdj（t-k）]

ξaj（t）=[aaj（k），faj（t-k）]（13）对式（13）中的各反射系数序列进行重构变换[15]，可得ξf=ξaj⊕ξdj⊕…ξd2⊕ξd1 （14）式中：ξf为PDBW法处理后的地质雷达信号。

2.2双正交小波预测反褶积法的应用流程

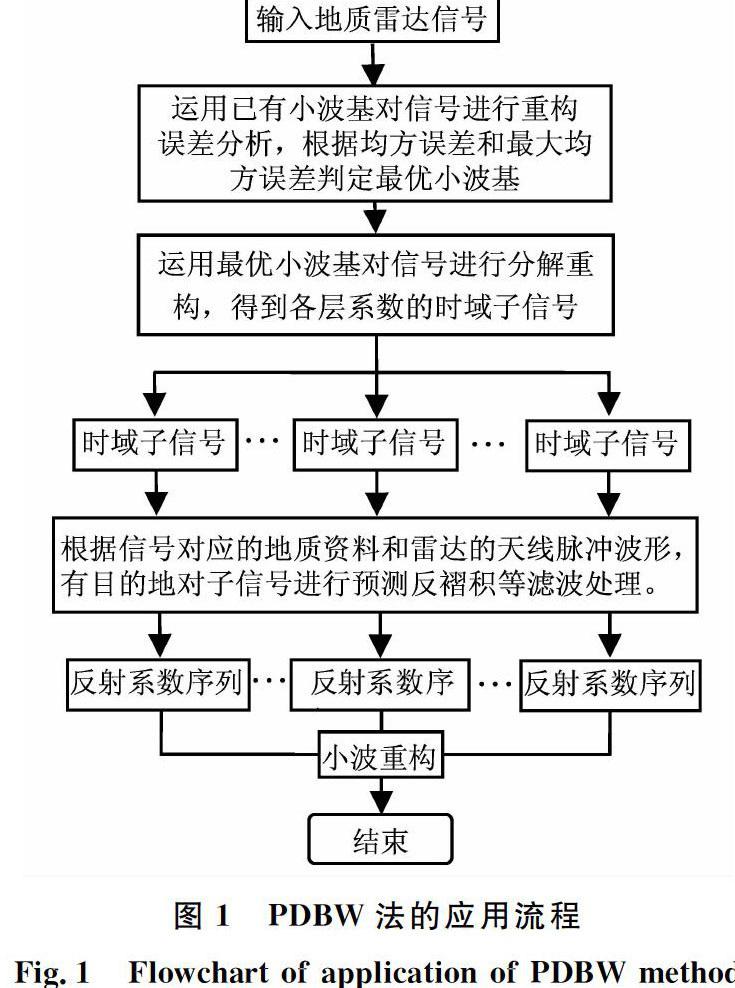
运用PDBW法处理地质雷达原始信号时，为了得到好的处理结果，应按照PDBW法的具体流程对信号进行处理，该法的应用流程见图1。

图1PDBW法的应用流程

Fig.1Flowchart of application of PDBW method此外，在PDBW法的应用过程中，还应遵从以下几个关键步骤：

1）最优小波基的选取不同小波基分析同一信号会产生不同的结果。在PDBW法中，小波分析的主要目的是对信号进行不同频段的小波分解和重构，因此，为了确保信号分析的稳定性，需要根据信号的小波重构误差确定最优小波基，从而保证信号分析的稳定性。目前，常用的判定指标有均方误差和最大均方误差[1617]。

2）地质资料及天线脉冲波形的掌握越多的掌握和了解信号对应的地质资料就越容易对目标反射波和多次回波出现的位置及波形能量的大小进行预判；不同的地质雷达，具有不同的天线脉冲波形，掌握天线脉冲波形的基本形式，有利于识别信号中的被测目标反射波。

3）预测反褶积等滤波方法的参数设置运用地质资料和脉冲波形判断各时域子信号中的噪声成分和反射波成分。针对各时域子信号选取相应的预测反褶积等滤波方法，并分别对各滤波方法中的参数进行设置。

3应用实例

在隧道质量无损检测中，衬砌内钢筋网和工字钢会严重影响衬砌厚度检测和背后脱空等病害的评估，因此，设计具有已知埋深和尺寸的铁板空腔检测实验，运用PDBW法对该实验检测信号进行处理，从而验证该法在地质雷达信号处理中的可行性。

3.1铁板空腔检测实验

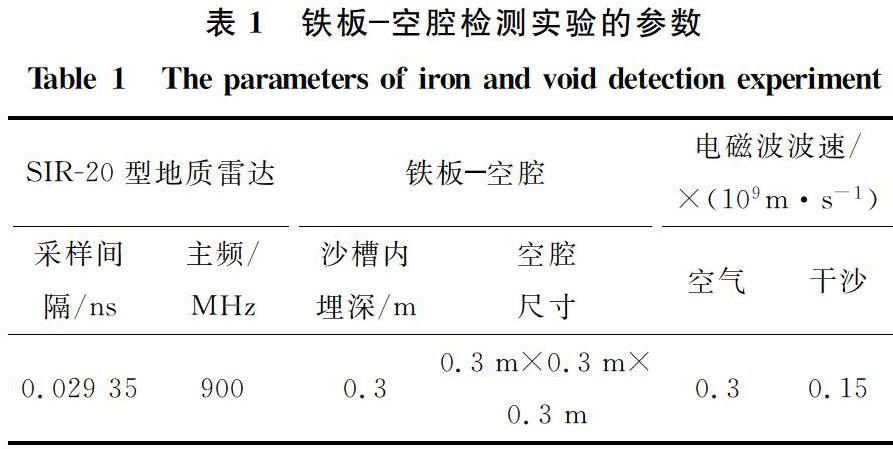
铁板空腔检测实验的具体设计及模型制作过程见表1、图2。表1铁板空腔检测实验的参数

Table 1The parameters of iron and void detection experimentSIR20型地质雷达铁板空腔电磁波波速/

×（109m·s-1）采样间

隔/ns主频/

MHz沙槽内

埋深/m空腔

尺寸空气干沙0.029 359000.30.3 m×0.3 m×

0.3 m0.30.15图2铁板空腔检测实验

Fig2.The iron and void detection experiment3.2实验检测信号的处理及对比分析

分别采用预测反褶积法和PDBW法对铁板空腔检测实验中的原始信号进行处理，通过信号的剖面图分析和单道信号的波形分析，研究两种方法对多次回波的抑制效果和对深部信号的识别效果。

1）原始信号的分析结果图3（a）为铁板空腔检测实验的原始信号，其中，存在明显的沙槽表面反射波、铁板反射波。由于薄铁板的本征阻抗较大，电磁波产生较强的铁板反射波和多次回波干扰，在图3（a）的区域1中存在明显的多次回波。根据波形分析法和倒相原理[1820]，对图3（b）中的第30道信号进行分析，用点1、2、3确定沙槽表面反射波、铁板反射波和多次回波的起始时间，起始时间分别为1468、5.488、8.776 ns，见表2。为了提高地质雷达探测分辨率和图像分析的准确性，需对原始信号进行滤波处理。

图3原始信号及其第30道信号

Fig.3The original signal and its No.30 trace2）预测反褶积法处理后信号的分析结果图4（a）为预测反褶积法处理后的信号，可以看出，区域1中的多次回波得到有效抑制，并在区域2中出现明显的反射波信号。图4（b）为处理后的第30道信号，根据波形分析法和倒相原理，运用点1、2表示沙槽表面反射波、铁板反射波的起始时间，用点3表示反射波3的起始时间，起始时间分别为1.468、5.488、8.834 ns，见表2。在表2中，预测反褶积法处理后信号中各反射波的起始时间与原始信号中各反射波的起始时间基本相等，所以，反射波3为多次回波。这表明，预测反褶积法只是对原始信号中的多次回波进行压制，并不能识别具有低信噪比的空腔底面反射波。

图4预测反褶积法处理后信号及其第30道信号

Fig.4The processed signal by predictive deconvolution

method and its No.30 trace3）PDBW法处理后信号的分析结果运用DB和Bior系列小波对原始信号进行重构误差分析，选取Bior2.4小波基为PDBW法中的最优小波。图5（a）为PDBW法处理后的信号，可以看出区域1中的多次回波得到有效抑制，并在区域2中出现明显的反射波信号。图5（b）为处理后第30道信号，根据波形分析法和倒相原理，运用点1、2确定沙槽表面反射波和铁板反射波的起始时间，用点3表示反射波3的起始时间，起始时间分别为1.497、5.459、7.631 ns，见表2。在表2中，与原始信号相比，PDBW法处理后信号中的反射波1和反射波2的起时间基本不变，但反射波3的起始时间发生明显变化，时间差值为1.145 ns。令反射波3为空腔底面反射波，并对PDBW法处理后的信号进行定量分析，得到铁板的计算深度和空腔的计算垂直尺寸分别为0.297 m和0.326 m，与实际值相比，计算误差为0.003 m和0.026 m，见表3。这表明PDBW法能准确识别空腔底面反射波，并能在压制多次回波的同时提高空腔底面反射波的信噪比，从而实现提高探测分辨率和图像分析准确性的目的。即上述分析结果验证了PDBW法在抑制多次回波干扰、识别深部信号和提高深部信號信噪比方面的可行性。

图5PDBW法处理后信号及其第30道信号

Fig.5The processed signal by PDBW method

and its No.30 trace表2处理后信号中反射波的起始时间

Table 2The start time of reflection waves in processed signals原始信號起始时

间/ns预测反褶积法处理后信号起始时

间/ns时间差

值/nsPDBW法处理后信号起始时

间/ns时间差

值/ns反射波11.4681.46801.4970.029反射波25.4885.48805.4590.029反射波38.7768.8340.0587.6311.145注：反射波1为信号中出现的第一道反射波信号，以此类推。

表3PDBW法处理后第30道信号的定量分析

Table 3The quantitative analysis of processed signal by PDBW实际值PDBW法处理后信号计算值误差值深度/m0.3000.2970.003垂直尺寸/m0.3000.3260.026注：深度为实验模型的埋深，即铁板的埋深；垂直尺寸为实验模型的厚度，即铁板表面到空腔底面之间的距离。4结论

1）根据地质雷达检测信号的固有特点，将传统的反褶积法与小波分析相结合，提出双正交小波预测反褶积法（PDBW法），并将PDBW法成功用于地质雷达检测信号的分析和处理。

2）PDBW法能有效抑制多次回波干扰，与预测反褶积法相比，PDBW法能够准确识别深部信号，提高深部信号的信噪比，从而改善地质雷达的探测分辨率和图像分析的准确性，并进一步提高了工程结构质量的检测效果。

3）PDBW法能有效应用于地质雷达检测信号处理，由于地震波与雷达波均遵循波的传播理论，并具有相同的线性褶积模型，使得PDBW法在理论上也适用于地震信号的处理，下一步将开展PDBW法对地震信号应用效果的研究与验证。

参考文献：

[1] BENEDETTO A，PAJEWSKI L. Civil engineering applications of ground penetrating radar [M]. Switzerland：Springer International Publishing， 2015.

[2] 曾昭发，刘四新，冯晅，等.探地雷达原理与应用[M].北京：电子工业出版社，2010.

[3] 凌同华，张胜，李升冉.地质雷达隧道超前地质预报检测信号的HHT 分析法[J].岩石力学与工程学报，2012，31（7）：14221428.

LING T H， ZHANG S， LI S R. Hilberthuang transform method for detection signal of tunnel geological prediction using ground penetrating radar [J]. Chinese Journal of Rock Mechanics and Engineering， 2012， 31（7）： 14221428. （in Chinese）

[4] BERNATEKJAKIEL A， KONDRACKA M. Combining geomorphological mapping and near surface geophysics （GPR and ERT） to study piping systems [J]. Geomorphology， 2016， 274 （1）： 193209.

[5] PONGSAK W， RAKTIPONG S， SOMNUK T， et al. A new method to determine locations of rebars and estimate cover thickness of RC structures using GPR data [J]. Construction and Building Materials， 2017， 140 （1）： 257273.

[6] 石刚，田养军，王亚琼，等.基于模糊分形脉冲反褶积的探地雷达信号处理[J].长安大学学报（自然科学版），2012，32（5）：7984.

SHI G， TIAN Y J， WANG Y Q， et al. Signal processing of groundpenetrating radar on the principle of deconvolution based on fuzzy fractal pulse [J]. Journal of Changan University （Natural Science Edition）， 2012， 32 （5）： 7984. （in Chinese）

[7] 苏茂鑫，李术才，薛翊国，等.基于反褶积的探地雷达高分辨率处理方法[J].浙江大学学报（工学版），2010，44（6）：12011206.

SU M X， LI S C， XUE Y G. Ground penetrating radars high resolution processing method based on deconvolution [J]. Journal of Zhejiang University （Engineering Science）， 2010， 44 （6）： 12011206. （in Chinese）

[8] ECONOMOU N， VAFIDIS A. GPR data time varying deconvolution by kurtosis maximization [J]. Journal of Applied Geophysics， 2012（81）： 117121.

[9] 王万里，杨午阳，魏新建，等.随机稀疏脉冲非线性反褶积[J].地球物理学进展，2014，29（4）：17801784.

WANG W L， YANG W Y， WEI X J， et al. Stochastic sparse spike nonlinear deconvolution [J]. Progress in Geophysics， 2014， 29（4）： 17801784. （in Chinese）

[10] CHANG Y F， MA Y， LIN C M， et al. Reverberation reduction in ultrasonic images via predictive deconvolution [J]. NDT & E International， 2008， 41（4）： 235241.

[11] TZANIS A. Detection and extraction of orientationandscaledependent information from twodimensional GPR data with tuneable directional wavelet filters [J]. Journal of Applied Geophysics， 2013， 89：4867.

[12] NGUYEN S T， BRIAN W H. Biorthogonal rational discrete wavelet transform with multiple regularity orders and application experiments [J]. Signal Processing， 2013， 93（11）： 30143026.

[13] MOURAD K， FETHI B R. Efficient automatic detection of QRS complexes in ECG signal based on reverse biorthogonal wavelet decomposition and nonlinear filtering [J]. Measurement， 2016， 94： 663670.

[14] MACEDO I A S， SILVA C B， FIGUEIREDO J J S. Comparison between deterministic and statistical wavelet estimation methods through predictive deconvolution： Seismic to well tie example from the North Sea [J]. Journal of Applied Geophysics， 2017， 136： 298314.

[15] FLETCHER P， SANGWINE S J. The development of the quaternion wavelet transform [J]. Singal Procsessing， 2017， 136： 215.

[16] 成謝锋，张正.一种双正交心音小波的构造方法[J].物理学报，2013，62（16）：168701.

CHENG X F， ZHANG Z. A construction method of biorthogonal heart sound wavelet [J]. Acta Physica Sinica，2013， 62（16）： 168701. （in Chinese）

[17] HACHICHA W， KAANICHE M， BEGHDADI A， et al. Noreference stereo image quality assessment based on joint wavelet decomposition and statistical models [J]. Signal Processing： Image Communication， 2017， 54： 107117.

[18] FENG X， LIANG W J， LIU C， et al. Application of Freeman decomposition to full polarimetric GPR for improving subsurface target classification [J]. Signal Processing， 2016， 132： 35343537.

[19] 杨艳青，贺少辉，齐法琳，等.铁路隧道衬砌地质雷达非接触检测模拟试验研究[J].岩石力学与工程学报，2011，30（9）：1761–1771.

YANG Y Q， HE S H， QI F L， et al. Simulation test of GPR noncontact detection on lining of railway tunnel [J]. Chinese Journal of Rock Mechanics and Engineering，2011，30（9）：1761–1771. （in Chinese）

[20] 胡进峰，周正欧.浅地层探地雷达目标探测和定位新方法[J].仪器仪表学报，2006，27（4）：371375.

HU J F， ZHOU Z O. Target detection and orientation in sursurface penetrating radar data [J]. Chinese Journal of Scientific Instrument， 2006， 27（4）：371375. （in Chinese）