非连续动态同步发电机组的空间正则化参数辨识方法

朱泽翔, 熊鸿韬, 马安安, 耿光超, 江全元

(1. 浙江大学电气工程学院, 浙江省杭州市 310027; 2. 国网浙江省电力有限公司电力科学研究院, 浙江省杭州市 310014)

0 引言

随着特高压电网的紧密互联及电网规模的不断增大,电网运行的安全稳定问题日益突出。同步发电机组作为电网的主要电源支撑,其动态模型的正确性严重影响着电力系统稳定仿真与控制措施结果的有效性[1-4]。

参数辨识是一种常用的建模手段,它根据特定输入信号校准模型参数,使得输出变量能够和测量匹配。并且相量测量单元(PMU)的广泛使用为同步发电机组在线参数辨识提供了实现基础[5]。相比于数据采集与监控(SCADA)系统而言,PMU具有更高的采样频率,能更好地捕捉电网动态行为,并且利用全球定位系统(GPS)信号同步不同节点采集的数据信息。文献[6-9]研究了利用在线测量数据对同步发电机组的动态元件进行参数辨识,而这些在线参数辨识方法大多需要对被测装备人为施加大扰动,然后单独对同步发电机组的各个控制系统参数进行辨识。一方面,此类方法需要在试验中额外施加扰动,存在试验费时、辨识过程复杂、设备损害等缺陷;另一方面,励磁系统或者调速系统与发电机之间的部分关联状态变量无法直接开展测量,所以无法对各子系统实施单独参数辨识。而利用发电机在线运用过程观测到的实际电网扰动进行辨识[10-12],无需人为施加扰动,也能够对发电机、励磁及调速系统一起进行联合参数辨识[13]。

但是,无论是利用人为施加扰动还是捕捉运行扰动的方法,都面临着一个共性问题:同步发电机组中存在非连续动态环节,如限幅、跳变、投切等,其运行参数通常由离线试验确定,在线辨识与校对的方法并不成熟。现有辨识方法大多利用智能算法[14-17]来处理非连续环节的触发变换。但由于智能算法存在收敛性差、计算效率低等不足,其很难在有限时间内或者有限迭代次数内给出一个理想的辨识结果。

针对上述不足,本文提出了一种非连续动态同步发电机组的空间正则化参数辨识方法。该方法利用Heavyside函数将非连续动态系统等效成一般微分方程表示的系统。然后,对等效系统进行离散化,将原参数辨识问题转变为非线性规划问题,并利用内点算法求解,以达到高效辨识的目的。另外,针对切换条件的辨识,提出了一种分阶段辨识方法以提高辨识结果的准确性。最后,大量的数值试验和实地测试验证了提出方法的有效性。

1 基于在线监测系统的发电机组参数辨识

基于在线监测系统的发电机组参数辨识方法可以只利用发电机的机端测量信息进行发电机组的参数辨识,并且能将发电机本体、励磁控制系统、调速系统的参数联合辨识,其基本框架见附录A图A1。

当电网发生故障或负荷显著变化导致发电机机端信号产生波动时,在线监测系统采集扰动期间与发电机相连的状态变量,并保存在数据库用于参数辨识。其中,采集的物理量包括:发电机机端电压、机端电流、有功和无功功率、励磁电压及电网频率等。若发电机组配置有电力系统稳定器(PSS),则需配置相应的采集装置,同步记录PSS输出信号。

在参数辨识过程实施之前,需要对上述采集的数据进行分类,即分为输入数据和输出数据。混合动态仿真理论[18]是一种电力系统常用的模型验证方法。该理论将输入数据输入动态模型中,计算动态模型输出与相应输出数据的匹配度来确定模型的正确性。在该理论中,与采用功率信号作为输入数据相比较,电压信号作为输入数据的动态模型输出更加准确[19]。因此,在数据信号的分类上,将测量的电压信号作为发电机模型的输入数据,其他的量测信号则作为输出数据。

根据上述数据分类方法,参数辨识问题可以构建为一个动态方程约束下的加权最小二乘优化问题,即

(1)

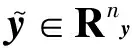
需要说明的是,由于同步发电机组的控制系统中存在大量的非连续环节,所以系统动态行为就不能用一个连续的微分方程表示,也就无法直接使用常规的优化算法进行求解。为解决这个问题,需要首先将非连续动态进行正则化,转换成连续形式的动态方程。

2 非连续动态模型空间正则化方法

2.1 非连续动态系统建模

同步发电机组在实际运行时,由于继电保护、控制器投切、限幅控制、跳跃环节及其他离散事件的存在,同步发电机组动态过程可表达为一个由不同切换边界分割的分段光滑微分方程。上述切换边界可以定义为:

Mk=x∈Rnx:gk(x)=0k=1,2,…,nk

(2)

式中:M为将状态变量空间分成不同区域的流形;g为不同离散事件的切换条件;下标k为切换条件的编号;nk为切换条件的总数目。

由此,问题(1)中描述同步发电机组动态行为的微分方程就可以详细地表示为:

(3)

式中:S为状态变量空间上被流形M分割的区域;上标l为区域的编号;ns为区域的总数量。

2.2 空间正则化方法

当求解如式(4)所示只含有一个切换边界的非连续动态方程问题时,Filippov理论[20]是一个常用的方法。该方法在非连续切换边界上构建一个由f1和f0组合的等效凸函数,而且该函数唯一隶属于切换边界的切平面。

(4)

但是,Filippov理论只能为单一边界问题提供一个滑动模态,对于多边界问题并不能提供一个有效的解决方法。而引入空间正则化方法[21]能够有效处理这个问题。该方法利用Heavyside函数将不同状态变量区域S的动态方程f构建成一个等效的微分方程,来描述非连续动态系统的动态过程。以式(4)为例,空间正则化后的动态方程表示为:

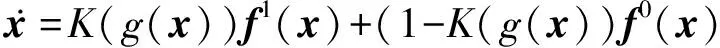
(5)

其中,K为Heavyside函数,其表达式如下:

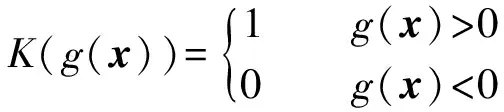
(6)

进一步,对于存在多个切换边界的非连续动态系统,利用空间正则化方法得到更一般的表达式:

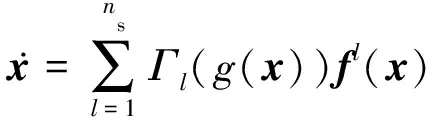
(7)

其中,Γl具有如下表达式:

(8)

该式由不同边界条件的Heavyside函数构成,用于选择隶属于l区域的状态变量。

3 非连续动态模型参数辨识方法

3.1 正则化模型的离散化

求解含动态方程约束的优化问题时,通常将微分方程约束进行离散化。这样原优化问题被转换为一个非线性规划(NLP)问题[22],然后选择适当的NLP算法进行求解。这类方法的好处在于能够有效地利用目前已有的NLP优化策略和计算资源来高效求解,并且在许多科学工程领域都体现了很好的鲁棒性和应用效果[23]。

但是,对于如式(3)所示的非连续空间表达式而言,由于离散化后的状态变量所处的区域无法确定,从而无法确定当前的动态过程的表达式,进而无法直接利用离散化公式。相比较而言,通过上述的空间正则化方法获得的等效动态模型(式(7)),能包含所有非连续动态方程的表示,故可以直接应用现有的离散化方法进行方程的转化。本文使用隐式梯形积分方法来进行动态方程约束的离散化,相应的离散化公式如下:

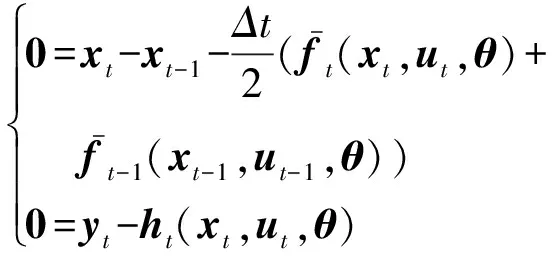
(9)

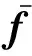
3.2 内点算法

由此,利用表达式(9),参数辨识问题(式(1))就可以写成一个如下所示的NLP问题:

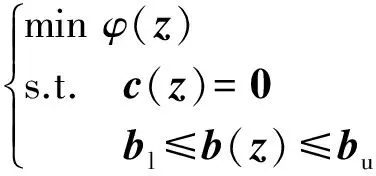
(10)

式中:c为离散化的等式约束;b为优化的不等式约束,下标u和l分别为不等式约束的上下界;z=[θ,s],它包含了待优化参数θ及离散化后的所有变量s,s=[x1,…,xnt,y0,y1,…,ynt],其中nt为离散时间的总个数。需要说明,状态变量初值也要放入θ中。

内点算法是一种高效求解大规模NLP问题的算法。该方法对不等式约束引入松弛变量,使其成为等式约束。然后利用Newton迭代法对KKT最优条件进行求解,通过使原对偶间隙最小,来寻找最优的结果。在该过程中最费时的过程就是求解一个如下所示的线性方程组:

(11)

式中:L和L′分别为NLP问题的拉格朗日函数及其扩展形式;λ为等式约束对应的拉格朗日乘子;H′为拉格朗日函数的海森矩阵的扩展形式。

由于参数辨识问题是一个低自由度的NLP问题,所以可利用简约空间技术[24]对式(11)进行高效的求解。并且,当使用多个情景数据一起进行参数辨识的时候,可以使用情景分解策略[25]将不同情景相关的计算分配到不同的计算单元上,以实现并行计算,加速问题求解。

3.3 切换条件辨识方法

在参数辨识问题中,参数的可辨识性分析是一个重要的部分,它可以通过分析参数轨迹灵敏度之间的相关性来确定参数可辨识能力的大小[26]。对于离散化后的动态方程,当方程成立时,辨识参数轨迹灵敏度可以利用雅可比矩阵计算得到,即

(12)

其中,由于s包含了离散化后的所有状态变量,所以参数相对于输出变量的灵敏度可以从中提取出来。

对于非连续动态系统,也可以利用该表达式计算相应的参数轨迹灵敏度。但需要特别说明的是,对于只存在于切换函数g的参数,其相应的轨迹灵敏度恒为零。

以单一切换边界为例,当参数仅显含于切换函数时,等式约束对于参数的雅可比矩阵为:

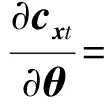
(13)

根据Heavyside函数K的形式(式(6)),可以发现在g绝大多数取值上的K相对于g导数常为0。并结合式(13)可知,辨识参数对应的轨迹灵敏度为零,也就意味着这个参数为不可辨识参数。因此利用Heavyside函数无法进行切换条件的辨识。

所以为了解决轨迹灵敏度恒为零时切换条件不可辨识的问题,就需要对Heavyside函数进行平滑化处理,使K相对于g导数不常为0。对于Heavyside函数,可以利用tanh函数进行近似逼近和平滑处理,相应的计算表述式如下:

(14)

式中:a为一个正的实数,不同a值下的近似函数与原函数的比较见附录A图A2。

随着a取值的增大,近似函数与原函数的相似度越高。但当近似函数与原函数过于相似时,相应的近似函数导数不为零的区域过窄,也就意味着相应参数可辨识性不佳。因此在选择a的取值时,只有平衡好两者关系,才能既保证系统动态行为的正确性,又兼顾切换条件的辨识效果。

4 标准测试系统算例分析

4.1 测试系统与模型设置

数值仿真测试系统采用IEEE 3机9节点系统,待辨识同步发电机组选为1号节点的发电机,发电机的额定容量为300 MVA,额定电压为13.5 kV。测试算例中,同步发电机本体模型使用GENTPF模型[27],其中发电机饱和特性使用指数函数来近似等效。发电机配置的励磁系统、PSS及调速系统的动态模型详见附录A图A3,而同步发电机及其控制系统相应的动态参数详细列于附录A表A1中。

励磁系统中的非连续环节为内部的限幅环节。PSS控制器中的非连续环节为输出的限幅环节及PSS投切环节。对于PSS投切环节,当机端电压在上限Vup和下限Vdn范围内的时候,PSS才能正常输出,否则无输入到励磁系统中。调速环节中的非连续环节同样包括输出的限幅环节及投切环节。当频率偏差小于0时,调速器汽门开启,切换到开动状态对应的传递函数;当频率偏差大于0时,调速器汽门关闭,切换到关闭状态对应的传递函数。在模拟扰动测试过程中,上述非连续环节均被激活,并且系统的动态行为随着非连续环节的触发而改变。

在数值试验过程中,测试系统的线路5-7在0.10 s发生三相短路故障,0.46 s切除故障。在故障期间,对发电机机端信号进行采样,采样时间为10 s,采样频率为50 Hz。

4.2 时域结果验证

首先,基于Heavyside函数的空间正则化方法,利用测量数据进行动态系统的参数辨识。在参数辨识过程中,PSS投切参数Vdn的初值与实际运行参数一致。图1展示了辨识结果与实测结果的时域比较。

从图1(a)至(c)中可以看出,发电机机端的有功功率、无功功率及PSS输出的辨识结果与实际测量偏差基本吻合。并且,图1(c)的PSS输出曲线说明,PSS输出的限幅器起到作用,限制了PSS的输出范围;图1(d)的机端电压显示,当故障开始时,机端电压迅速跌落,故障切除后,机端电压才恢复到正常水平,在故障期间PSS输出为零,说明PSS投切环节起作用使PSS在故障阶段退出运行;图1(e)中可以看出,由于故障期间调速器汽门关闭,实际机械输出为汽门关闭状态对应的输出,故障后由于频率振荡,汽门的状态在两者之间切换。

进一步将本文提出的空间正则化方法与遗传算法进行了比较,其中遗传算法的种群数选为20,最大迭代次数选为200。不同方法的目标函数、参数误差、迭代次数及计算耗时的比较结果列于表1中。

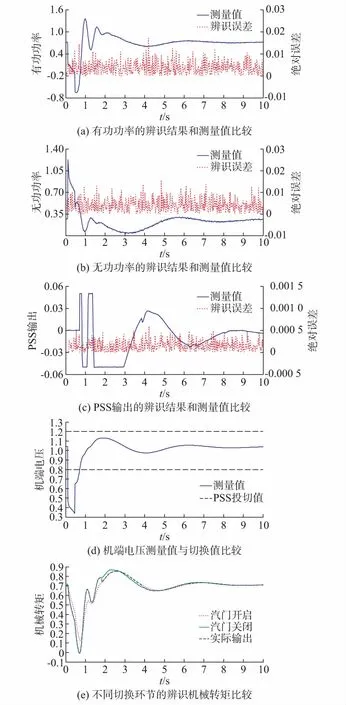
图1 输出变量的辨识结果与测量结果比较Fig.1 Comparison between estimation results and measurement results for output variables

优化算法目标函数参数误差/%迭代次数计算耗时/s遗传算法9．43311．402001176空间正则化方法0．2863．06101．892

表1结果说明:遗传算法在寻优的过程中,需要大量的计算,并且达到最大迭代次数时,也无法找到一个准确的结果,而所提出的空间正则化方法在各个方面均优于遗传算法。较小的目标函数和辨识误差也说明,提出的方法能够有效地处理非连续动态环节,具有较好的辨识效果。

4.3 切换条件辨识分析

从时域比较结果可知,对那些能够显式表示在动态方程中的非连续切换参数,如限幅环节的参数,利用Heavyside函数能够获得较好的辨识。但对于PSS投切参数,由于其仅存在于切换条件中,使用Heavyside函数不能辨识,需对其进行平滑处理。

为了分析不同平滑函数下PSS投切条件的辨识结果,这里比较了近似函数不同参数a下,以及Vdn不同初值下的辨识结果,详细结果列于表2中。

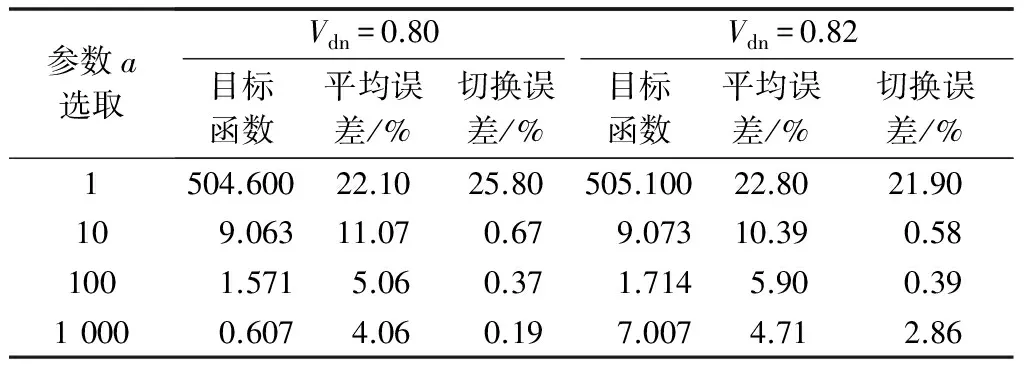
表2 不同参数下近似函数对辨识结果的影响Table 2 Influence of approximation functions on identification results with different parameters

表2数据显示,当Vdn初值为0.80时,参数a取值越大,目标函数越小,同时参数的平均辨识误差也越小。这一结果说明,在切换条件初值准确时,近似函数与原函数越相近,相应辨识效果越好。当Vdn初值为0.82时,在a取值较小时,由于近似函数不能反映系统动态行为,辨识误差和切换条件辨识误差均较大;当a取值较大时,整体的参数辨识误差变小,但是切换条件的辨识误差较大,说明由于等效函数非零域变窄,切换条件无法得到较好辨识;相比较而言,当a取值为100时,切换参数不仅能够较好地辨识,而且参数的整体平均误差也较小。

进一步,当Vdn取值为0.82时对不同近似函数的算法收敛性进行了分析,结果见附录A图A4。当近似函数的a取值为100时,算法经过13次迭代即收敛,具有良好的收敛性。这也更进一步说明了a取值在100时更适用于切换条件不确定时的非连续动态系统参数辨识。

然而,从上述辨识误差的结果可以发现,即使a取值为100,参数整体误差依然较大;并且在实际应用时,无法根据近似函数的辨识结果选择准确的切换参数。为了克服这个问题,算法实施可以分两阶段进行：第1阶段,利用不同的近似函数分别进行切换条件的辨识,获得不同参数a下的切换参数;第2阶段,基于不同辨识的切换参数,分别再利用Heavyside函数进行其他动态参数的辨识,其中目标函数最小组的辨识参数就是最终的辨识结果。

利用这种方法,对Vdn初值为0.82的情况进行了测试,相应的辨识结果如表3所示。

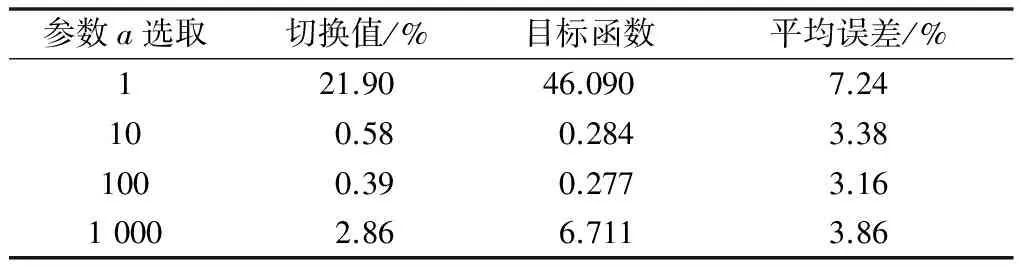
表3 不同切换条件下的参数辨识结果Table 3 Parameter identification results with different switching conditions

表3数据表明,第2阶段的目标函数越小,对应第1阶段辨识切换条件误差和所有参数平均辨识误差也越小。这也表明利用目标函数选择辨识结果是有效的。同时,a取值为100时辨识效果最佳,这时参数平均辨识误差为3.16%,与之前的5.90%相比,提高了2.74个百分点。这也说明了所提出的分阶段方法能够有效提高参数辨识精度。

5 实际机组辨识算例分析

应用本文提出的方法对浙江省某电厂的同步发电机组进行了实地测试。测试发电机额定电压20 kV,额定功率742.8 MVA,额定励磁电压和电流分别为142.6 V和1 695 A,励磁输出上下限Vmax和Vmin分别设置为9.05(标幺值)和-6.75(标幺值),其中被测励磁控制系统模型见附录A图A5。

由于在发电机实际运行时励磁系统输出很难达到限幅值,所以利用大扰动信号对空载下的发电机进行测试。在试验过程中,先施加-15%的励磁电压跌落的指令改变励磁电压,待发电机运行平稳后,再次施加励磁电压上升的指令,使机端电压返回正常值。试验过程的励磁电压输出由厂站测量装置进行采样,采样频率为100 Hz。

图2展示了扰动过程中励磁电压的参数辨识结果曲线和实际测量曲线。

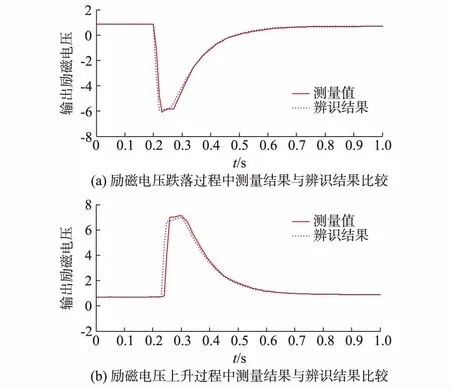
图2 实际数据的时域比较Fig.2 Time-domian comparision of actual data

由图2可知,当励磁电压下降或上升到一定范围时,不再大幅度变化,说明励磁系统的输出限制器起到作用,限制励磁系统输出。而且,辨识曲线和实际测量曲线基本吻合,说明本文算法能够很好地处理相应的非连续环节。Vmax和Vmin的辨识结果分别为8.90和-6.64,与设置值最大偏差只有0.15(标幺值),说明本文方法能够很好地应用于实际的同步发电系统。

6 结语

本文提出了一种非连续动态同步发电机组的空间正则化参数辨识方法。该方法利用Heavyside函数将不同状态空间的动态方程重新构建为一个等效的动态方程。并利用内点算法对离散化等效方程约束的优化问题进行求解,实现非连续系统的参数辨识。一系列的仿真实验和实际测试结果表明,所提出的方法能够准确、高效地辨识非连续系统的动态参数。当非连续切换条件需要辨识时,所提出的分阶段辨识方法能够兼顾系统非连续动态特性和切换条件辨识结果的准确性。

综上所述,由于具备处理非连续环节的能力,本文方法可以扩展到直流输电、风力发电、光伏发电等涉及电力电子设备建模的领域;同时,本文方法的高效性,使其在基于广域测量的电力系统全网辨识领域也具有良好的应用前景。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参 考 文 献

[1] 王锡凡,方万亮,杜正春.现代电力系统分析[M].北京:科学出版社,2003.

[2] KOSTEREV D N, TAYLOR C W, MITTELSTADT W A. Model validation for the August 10, 1996 WSCC system outage[J]. IEEE Transactions on Power Systems, 1999, 14(3): 967-979.

[3] 周孝信,鲁宗相,刘应梅,等.中国未来电网的发展模式和关键技术[J].中国电机工程学报,2014,34(29):4999-5008.

ZHOU Xiaoxin, LU Zongxiang, LIU Yingmei, et al. Development models and key technologies of future grid in China[J]. Proceedings of the CSEE, 2014, 34(29): 4999-5008.

[4] 李兆伟,吴雪莲,庄侃沁,等.“9·19”锦苏直流双极闭锁事故华东电网频率特性分析及思考[J].电力系统自动化,2017,41(7):149-155.DOI:10.7500/AEPS20160910002.

LI Zhaowei, WU Xuelian, ZHUANG Kanqin, et al. Analysis and reflection on frequency characteristics of East China grid after bipolar locking of “9·19” Jinping-Sunan DC transmission line[J]. Automation of Electric Power Systems, 2017, 41(7): 149-155. DOI: 10.7500/AEPS20160910002.

[5] 王茂海,齐霞.计及磁饱和的同步发电机内电势幅值测量方法[J].电力系统自动化,2016,40(6):134-138.DOI:10.7500/AEPS20150715002.

WANG Maohai, QI Xia. An internal voltage measuring method for generators taking saturating into account[J]. Automation of Electric Power Systems, 2016, 40(6): 134-138. DOI: 10.7500/AEPS20150715002.

[6] 孙黎霞,鞠平,高运华,等.基于Park模型的同步发电机参数辨识[J].中国电机工程学报,2009,29(19):50-56.

SUN Lixia, JU Ping, GAO Yunhua, et al. Parameter estimation of synchronous generation based on Park model[J]. Proceedings of the CSEE, 2009, 29(19): 50-56.

[7] 罗建,冯树辉,蔡明,等.基于可观测量的同步发电机参数的时域辨识[J].电力系统自动化,2011,35(7):24-27.

LUO Jian, FENG Shuhui, CAI Ming, et al. Time domain parameter identification of synchronous generator based on measurable variables[J]. Automation of Electric Power Systems, 2011, 35(7): 24-27.

[8] 王良,沈善得,朱守真,等.基于EE模型的励磁系统参数时域辨识法[J].电力系统自动化,2004,26(8):26-29.

WANG Liang, SHEN Shande, ZHU Shouzhen, et al. A method of time domain identification based on EE model for the excitation system parameters[J]. Automation of Electric Power Systems, 2004, 26(8): 26-29.

[9] 杨小东,董宸,卢文华,等.基于遗传算法的水轮发电机组调速系统参数辨识[J].继电器,2006,34(1):27-30.

YANG Xiaodong, DONG Chen, LU Wenhua, et al. Parameter identification for hydraulic turbine governing systems based on genetic algorithm[J]. Relay, 2006, 34(1): 27-30.

[10] 伍双喜,吴文传,张伯明,等.用PMU实测数据辨识同步发电机参数的关键问题[J].电力系统自动化,2012,36(17):50-55.

WU Shuangxi, WU Wenchuan, ZHANG Boming, et al. Key issues of synchronous generator parameter identification using PMU measurements[J]. Automation of Electric Power Systems, 2012, 36(17): 50-55.

[11] 伍双喜,张伯明,吴文传,等.基于实测系统扰动的同步发电机参数辨识与验证[J].电网技术,2012,36(11):87-93.

WU Shuangxi, ZHANG Boming, WU Wenchuan, et al. Identification and validation for synchronous generation parameters based on recorded on-line disturbance data[J]. Power System Technology, 2012, 36(11): 87-93.

[12] 邱健,于海承,环加飞,等.同步发电机非线性模型的期望最大辨识[J].电网技术,2016,40(8):2376-2382.

QIU Jian, YU Haicheng, HUAN Jiafei, et al. Maximum expectation identification of nonlinear model of synchronous generator[J]. Power System Technology, 2016, 40(8): 2376-2382.

[13] HUANG Z Y, DU P W, KOSTEREV D, et al. Generator dynamic model validation and parameter calibration using phasor measurements at the point of connection[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1939-1949.

[14] 张兆阳.基于PMU的励磁系统参数辨识研究[D].北京:华北电力大学,2014.

[15] 毛晓明,蔡永智,赵勇.采用最大-最小蚁群算法的励磁系统参数辨识[J].电力系统及其自动化学报,2015,27(5):51-55.

MAO Xiaoming, CAI Yongzhi, ZHAO Yong. Excitation system parameter identification via maximum-minimum ant system[J]. Proceedings of the CSU-EPSA, 2015, 27(5): 51-55.

[16] 孔祥平,袁宇波,高磊,等.基于差分进化算法的光伏并网逆变器控制器参数辨识方法:201510472410.0[P].2017-11-21.

[17] 孔祥平,袁宇波,阮思烨,等.面向故障暂态建模的光伏并网逆变器控制器参数辨识[J].电力系统保护与控制,2017,45(11):65-72.

KONG Xiangping, YUAN Yubo, RUAN Siye, et al. Controller parameter identification of the grid connected PV inverter for fault transient modeling[J]. Power System Protection and Control, 2017, 45(11): 65-72.

[18] KOSTEREV D N. Hydro turbine-governor model validation in Pacific northwest[J]. IEEE Transactions on Power Systems, 2014, 19(2): 1144-1149.

[19] 伍双喜,吴文传,张伯明,等.用PMU量测设置V-θ节点的混合动态仿真验证策略[J].电力系统自动化,2010,34(17):12-16.

WU Shuangxi, WU Wenchuan, ZHANG Boming, et al. A hybrid dynamic simulation validation strategy by settingV-θbuses with PMU data[J]. Automation of Electric Power Systems, 2010, 34(17): 12-16.

[20] FILIPPOV A F. Differential equations with discontinuous right-hand sides[M]. Dordrecht, Netherlands: Springer Science+Business Media, 1988.

[21] SOTOMAYOR J, TEIXEIRA M A. Regularization of discontinuous vector fields[C]// Proceedings of International Conference on Differential Equations, 1996, Lisbon, Portugal: 207-223.

[22] JIANG Q Y, HUANG Z G. An enhanced numerical discretization method for transient stability constrained optimal power flow[J]. IEEE Transactions on Power Systems, 2010, 25(4): 1790-1797.

[23] ZAVALA V M, LAIRD C D, BIEGLER L T. Interior point decomposition approaches for parallel solution of large-scale nonlinear parameter estimation problems[J]. Chemical Engineering Science, 2008, 63(19): 4834-4845.

[24] JIANG Q Y, GENG G C. A reduced-space interior point method for transient stability constrained optimal power flow[J]. IEEE Transactions on Power Systems, 2010, 25(3): 1323-1240.

[25] 王云,江全元,宋军英,等.电力系统发电机参数辨识的多情景并行内点算法[J].电力系统自动化,2013,37(18):75-81.

WANG Yun, JIANG Quanyuan, SONG Junying, et al. Multi-scenario parallel interior algorithm for generator parameter identification in power systems[J]. Automation of Electric Power Systems, 2013, 37(18): 75-81.

[26] 郭磊,鞠平,王红印,等.电力系统多台发电机参数的整体辨识[J].电力系统自动化,2011,35(17):44-50.

GUO Lei, JU Ping, WANG Hongying, et al. System wide parameter identification of multi-generators in power systems[J]. Automation of Electric Power Systems, 2011, 35(17): 44-50.

[27] WEBER J. Description of machine models GENROU, GENSAL, GENTPF and GENTPJ[R]. Champaign, USA: PowerWorld Corporation, 2015: 6-13.