基于集成学习的孤岛微电网源—荷协同频率控制

王德志, 张孝顺, 刘前进, 余 涛, 潘振宁

(1. 华南理工大学电力学院, 广东省广州市 510640; 2. 广东省绿色能源技术重点实验室, 华南理工大学电力学院, 广东省广州市 510640)

0 引言

面对分布式电源(DG)及主动负荷的大量并网,微电网技术能够灵活、系统地将DG和主动负荷组为一个整体,从而有效解决电力系统与DG间的矛盾[1]。但当微电网运行于孤岛模式时,缺少了大电网的支撑,发电侧有功出力与负荷的不匹配将会导致更严重的频率失稳问题,因此频率控制是孤岛微电网的一项关键运行任务。

迄今为止,众多专家学者针对微电网的频率控制进行了大量研究。文献[2]提出一种新颖的比例—积分(PI)控制器,对比传统的PI控制器能够有效提高其动态响应特性。而在孤岛微电网的二次调频中,为解决集中控制器与本地控制器之间的通讯延迟影响问题,文献[3]提出了一致性协同的框架,通过各机组件的通讯互补可以有效解决通讯丢包对功率分配的影响。文献[4]提出了一种基于最小阶观测器的光柴混合微电网的频率优化控制策略来减小因出力不稳定而引起的微电网的频率偏差。文献[5]提出一种有效的分布式发电控制方法,该方法能够实现连续的有功功率平衡和自我频率恢复。然而,包括以上所提的大多数研究工作主要集中于发电侧的控制策略,而缺少需求侧可控负荷与供给侧协同辅助调频问题,文献[6]指出了需求响应参与辅助服务市场能够有效提升电力市场的效率和系统运行稳定性。因此,文献[7]提出了利用冰箱来进行微电网二次调频的策略,文献[8]也指出了需求侧的资源具有良好的可控潜力来作为电网的调频备用。另一方面,现有集中控制器通常是根据固定调节因子来分配总功率指令,如按相同可调容量比例分配(PROP)算法[9],缺少考虑不同机组调节特性,如发电机发电成本和爬坡速率。因此,综合考虑多种调节因子有助于提高机组响应的动态性能和经济性。

基于以上两个考虑,本文提出一种考虑孤岛微电网下的源—荷协同频率控制模型,通过最小化所有参与机组的最大爬升时间及考虑分布式发电机组和负荷的调节成本来达到快速、经济地进行频率控制目的。但该问题是一个非光滑、非线性优化问题,传统基于梯度的优化算法容易因初值选取不恰当而陷入局部最优,而不基于模型的启发式优化算法在全局优化上则更加灵活、高效,也更适用于求解该问题。然而一般的启发式优化算法计算时间长,尤其是当控制变量维数增多时,难以满足频率控制在线优化要求[10]。为解决该问题,本文还提出了基于集体智慧的集成学习(EL)算法,该算法由多个子优化器及一个学习集中器组成。其中不同的子优化器通过不同的优化机制来提高探索能力,而学习集中器利用各子优化器当前的结果来实现有效的深度挖掘,以此来保证获得高质量的最优解。基于强化学习[11](RL)的学习集中器不仅可以通过自我探索和开发来指导学习,还可以实现从源任务到新任务的知识迁移[12],因此EL算法的计算时间将显著降低,足以满足频率控制在线优化要求。

1 孤岛微电网源-荷协同频率控制模型

1.1 负荷聚合商辅助调频

本文引入负荷聚合商(load aggregator,LA)[13]对大规模家庭负荷进行聚合,从而避免了“维数灾难”问题。家庭用户通过家庭能量管理系统[14](HEMS)来与LA进行通信,上传信息和执行LA下达的开关控制命令。家庭用户可参与设备主要考虑空调、电冰箱和电热水器三种温控设备,由于其热动态过程具有一定的延迟性,短时间地改变设备开关状态可以有效响应系统功率需求从而参与辅助调频[15]。

实时评估LA的储备能力是LA参与辅助调频服务的必要条件。以制冷型设备为例,假设所控温度需保持在Tmin至Tmax,如果温度超过Tmax,则设备自动开启；如果温度低于Tmin,则设备自动关闭,如图1情形Ⅰ所示。因此,当温度处于舒适度范围内,且开关处于关闭状态时,通过将其开启可以提供频率控制的下调储备,见图1情形Ⅱ。类似地,当开关处于开启状态时,通过将其关断可以提供上调储备,见图1情形Ⅲ。制热型设备的评估方式可类比制冷型设备,但制热型设备开关开启温度将会上升,而关断则造成温度下降。

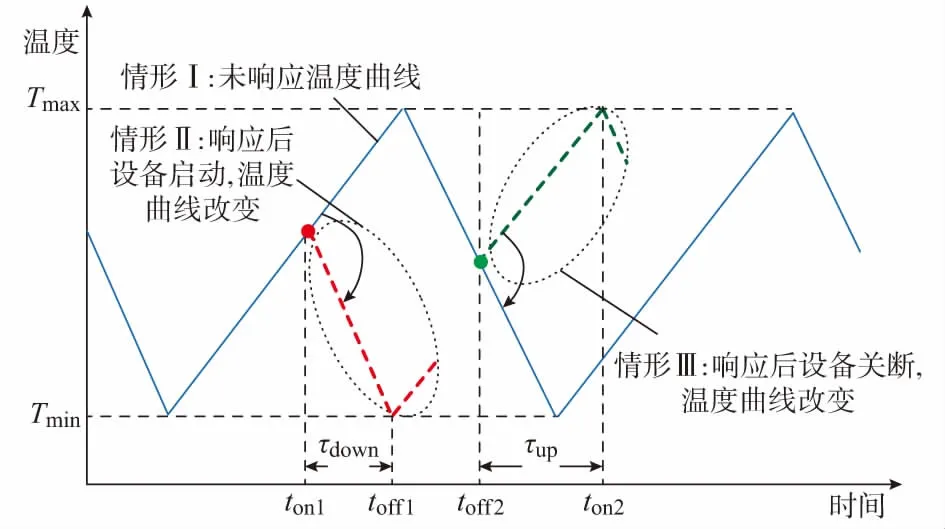
图1 制冷型设备容量评估示意图Fig.1 Schematic diagram of reserve capability for cooling equipment

通过评估从关断/开启时刻至温度曲线达到边界Tmax/Tmin的时间τup/τdown，以此来制定参与设备的优先级。因为该段时间内并不会影响用户的舒适度要求，故该段最大参与时间越长，其优先级越高。当LA与电网交易时，优先级高的设备优先参与辅助调频。此外，为了较好地辅助微电网调频，并满足用户的舒适度需求，本文规定只有当最大参与时间大于15 min才会加入辅助调频序列。因此，LA可参与辅助调频的上调容量等于辅助调频序列中所有可关断温控设备总额定功率，同理LA下调容量等于辅助调频序列中所有可开启温控设备总额定功率。当LA实际参与辅助调频并接受了微电网的功率指令后，本文考虑不同设备之间特性差异，LA的下层分配按其类型的总可调容量比例进行分配。

1.2 家庭可控设备的数学模型

注意到每个温控设备的最大参与时间与其当前运行状态和温度变化特征有关，本节对空调、电冰箱和电热水器进行建模，以便LA进行最大参与时间的评估。

1)空调负荷建模

由热量平衡原理建立空调热力学模型[16]为：

(1)

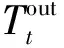
2)电冰箱负荷建模

电冰箱用电特性可用数学模型描述[17]为：

(2)

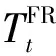
3)电热水器负荷建模

由能量守恒原理，电热水器模型可描述为[18]：

(3)

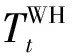
由式(1)至式(3)可知，电冰箱和电热水器的模型为线性方程，故其最大参与时间可进行直接求解；而空调模型为超越方程，可利用牛顿迭代法进行求解。再通过对各类型设备的最大参与时间进行降序排列，即可得到每种类型设备的优先级。

1.3 源—荷协同频率控制下功率分配模型

由于负荷扰动或运行故障等会造成系统有功功率失衡，致使频率偏离标称值。通过比例—积分(PI)控制器可根据频率偏差量Δf来跟踪功率偏差值。本文所提源—荷协同频率控制模型，即通过最小化所有参与机组的最大爬升时间及考虑DG和LA的调节成本来将ΔPS分配给各DG和LA。

采用经济调度常用的二次函数,DG的发电成本为：

(4)

式中：Cm为第m个DG的发电成本函数;Pm为第m个DG的发电功率；am，bm，cm分别为第m个DG发电成本的各次系数。另外，本文规定LA调整电量部分按当前电价的30%作为用户的报酬。

由于温控设备开合时间与机组调节时间相比可忽略不计，因此本文所提的孤岛微电网源—荷协同频率控制下功率分配模型的目标函数可设计为：

(5)

(6)

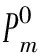
2 基于集体智慧的集成学习算法

2.1 集成学习优化框架

本文借鉴众包竞赛思想[19]引入集体智慧来加速EL算法在知识矩阵初始形成阶段的探索与开发过程。众包竞赛是企业为了解决创新过程中遇到的疑难问题向外部“悬赏”解答方案。各个子优化器根据自身智慧水平对发布问题给出解答，而学习集中器通过与各解答者交流来进行RL学习，更新知识矩阵，经反复交流后可以得出一个收敛的最优解。

2.2 学习集中器

RL是一种不基于模型的机器学习，可以从智能体和环境之间的连续交互中实现目标，其中Q学习是最著名和广泛使用的RL技术之一[20]。本文采用Q学习作为学习集中器学习和存储知识的主体，但由于传统的Q学习只能用于离散变量的优化，借鉴文献[21]提出的基于关联记忆的二进制状态动作链，即连续控制变量xi可由二进制字符串来表示，每个二进制位都会对应一个2×2规模的知识矩阵Qil，原来的大规模知识矩阵Q就能有效分解和存储，同时可以保证连续控制变量的动作精度和知识更新速率。因此，在二进制字符串关联记忆模式下，知识矩阵更新过程可为：

(7)

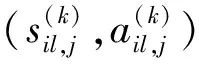
与单智能体的Q学习相比，基于群智能技术[22-23]的Q学习通过共享知识矩阵可以在未知环境中进行开发和探索，而不是围绕当前最佳个体的贪婪搜索或在整个搜索空间中的随机搜索。为了实现探索与开发之间的平衡，根据ε-Greedy规则[24]进行动作选择。即

(8)

式中：q0为[0,1]中均匀分布的随机值；ε为贪婪行为(开发)的开发率；arand为随机动作(探索)。

2.3 学习集中器与子优化器交互机制

众包竞赛中，参与的解答者数量及其之间的差异性将会影响到任务完成的速度与质量，并且其差异性越大越能够获得高质量的最优解。因此本文中EL算法引入了多种二进制优化算法来作为子优化器，包括遗传算法(GA)[25]、6种不同转换方式的二进制粒子群算法(BPSO)[26]、二进制蝙蝠算法(BBA)[27]、二进制蜻蜓算法(BDA)[28]和二进制灰狼算法(BGWO)[29]等，通过不同的优化机制，为学习集中器提供多样化的学习样本。同时，由于子优化器并行独立求解，极大节省了总计算时间。另外，子优化器与学习集中器之间需每隔一段时间按式(9)至式(11)进行交互：

l=1,2,…,L}

(9)

(10)

(11)

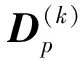
2.4 知识迁移

传统的启发式优化算法有一个共同的特点，每一次优化任务的求解都是孤立的，在执行新的任务时必须重新初始化，为了较好地利用过去的优化信息，EL算法引入了从源任务到新任务的知识迁移，其具体可描述为：

(12)

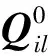
3 基于EL算法的孤岛微电网源—荷协同频率控制求解设计

3.1 奖励函数设计

根据问题及约束式(5)和式(6)，结合蚁群优化(ACO)的合作机制[30]和可行解质量越高其奖励值越大的原则，可设计该问题的奖励函数为：

(13)

(14)

(15)

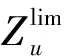
3.2 知识迁移设计

本文通过将可能的总功率指令ΔPS分为几个间隔来确定源任务：

(16)

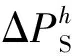
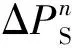
(17)

3.3 算法求解流程

基于EL算法的孤岛微电网源—荷协同频率控制的执行过程如图2所示。

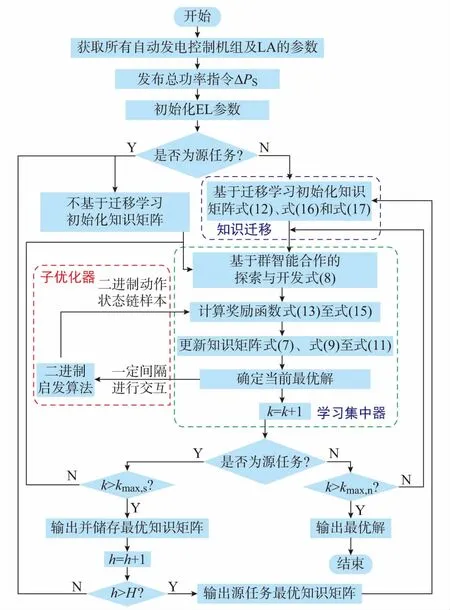
图2 基于EL算法的孤岛微电网源-荷协同频率控制流程图Fig.2 Overall execution procedure for generation-consumption coordinated frequency control based on EL method

图中kmax,s是源任务的最大迭代次数，kmax,n是新任务的最大迭代次数。当遍历所有源任务后，新任务将根据源任务的最优知识矩阵进行初始化。此外，考虑到各DG与LA的储备容量会随时间和负荷的变化而变化，且一般各机组的储备容量在15 min内不会有太大变化，因此本文设定预学习的实施周期设置为15 min，即每15 min重新获得各DG和LA的备用容量参数来进行下一个时段不同源任务的预学习，以保证上述知识迁移方法不受其他因素影响。

4 仿真算例

4.1 仿真模型搭建及参数设置

本文搭建了包含微型燃气轮机(MT)、燃料电池(FC)、柴油机(DS)、光伏发电机(PV)、风力发电机(WT)和LA的孤岛微电网模型，如附录A图A1所示，其中PV和WT不参与调频。各机组的相关参数[31]见表1，LA评估分级模型参数参见文献[14-16]，温控设备参数见表2，分时电价信息与孤岛微电网基础负荷曲线见附录A图A2。

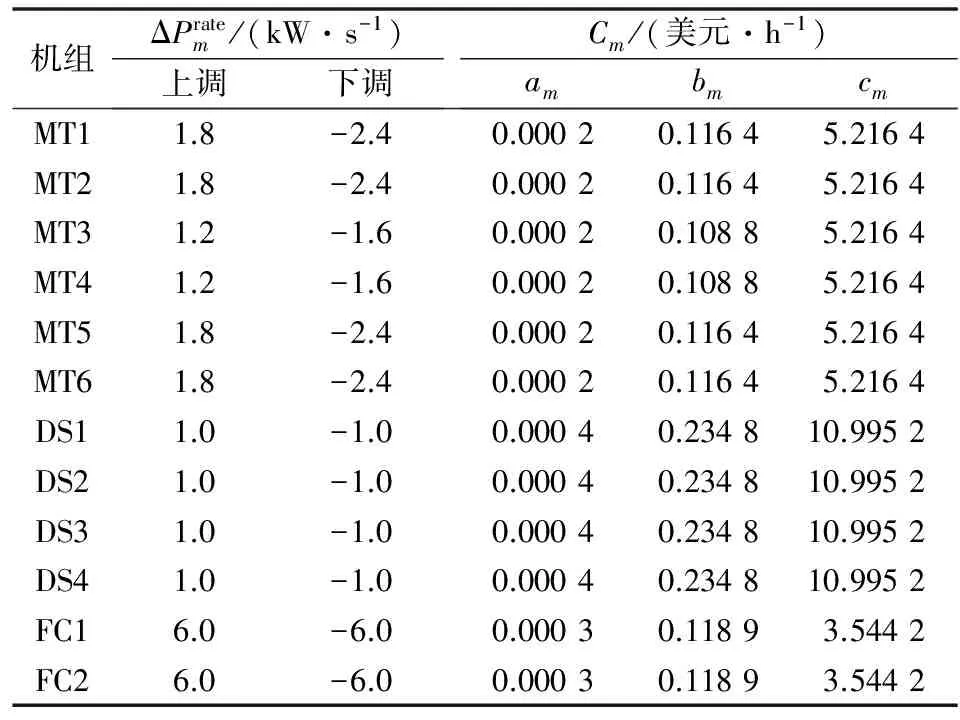
表1 DG参数列表Table 1 Parameters list of DGs

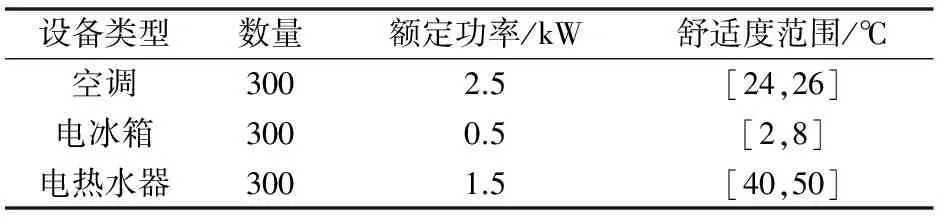
表2 温控设备参数Table 2 Parameters of thermostatically controlled loads

为对比EL 算法在求解孤岛微电网源—荷协同频率控制的寻优性能，本文引入PROP算法、GA、粒子群优化算法(PSO)[20]、群搜索优化算法(GSO)[21]和内点法(IPM)，对比算法的种群规模和最大迭代步数均设为150，EL算法的具体参数设置值见附录A表A1。仿真在CPU为英特尔i7-6700、主频3.4 GHz、内存16 GB的计算机运行计算。

4.2 EL算法预学习

本文将ΔPS离散分为12个间隔，即{[-300,-250),[-250,-200),…,[250,300]}。如附录A图A3所示，在ΔPS=200 kW时，EL算法知识矩阵的ΔQ能够在50次迭代之后基本达到收敛。同时，各子优化器基于各自优化机制均获得了该源任务下较小的目标函数值，以此保证了学习集中器能够获得一个高质量的最优解。同理可得其他源任务的最优知识矩阵。

4.3 在线优化与结果对比

4.3.1在线优化收敛结果

由图2可知，ΔPS=225 kW的新任务可以利用相邻两个源任务的最优知识矩阵(即ΔPS=200 kW和ΔPS=250 kW)，其相似度在新任务和这两个源任务之间分别等于0.5，与其他源任务的相似度则为0。如附录A图A4所示，不同算法在新任务ΔPS=225 kW下的收敛曲线对比，相比于其他优化算法，基于知识迁移后的EL算法能够快速逼近更高质量的最优解，且所有算法的执行时间均小于本文设定的控制周期(4 s)，其中，EL算法在线优化的执行时间仅为不到1.5 s，完全满足孤岛微电网源—荷协同频率控制的在线优化，这也验证了知识迁移和集体智慧在收敛速度和收敛结果上的优越性。

4.3.2结果分析与比较

1)阶跃扰动测试

为了测试EL算法的实时性能，在孤岛微电网添加了ΔPM=225 kW的功率失衡。附录A图A5提供了在12:00—12:10，当ΔPM=225 kW时，在不同算法下获得的实时在线优化结果。从附录A图A5(a)可以看出,各算法下均能有效平衡功率失衡，部分算法存在功率波动较大的现象，是由于算法前后两个优化结果存在较大差异导致，而IPM结果与其初值的给定有较大的关系，因此可能造成其陷入局部最优。由附录A图A5(b)可以看出，频率偏差均能够快速回复到零值，且EL算法的频率偏差最小，而在附录A图A5(c)中,EL算法的总运行成本接近最小，这说明了EL算法能够有效兼顾机组爬升时间与运行成本。从附录A图A5(d)可以看出，LA,FC1和FC2承担了大部分出力，这是由于它们具有较快的爬升速率和相对较低的运行成本。

附录A图A6展示该阶跃扰动下，LA所属的部分空调、电冰箱和电热水器所控温度曲线。有效参与的温控设备通过闭合开关来参与功率正调过程，并从附录A图A6可看出，参与的设备所控温度均在用户可接受温度范围内，表明了利用优先级机制的LA辅助调频方法能够有效满足用户舒适度要求。

2)全日随机扰动测试

为了进一步研究EL算法的连续实时控制性能,本算例在孤岛微电网的模型上进行了24 h随机扰动实时仿真。其中，包含白噪声的随机方波负荷，扰动周期为3 600 s。如附录A图A7所示，EL算法仍能够有效匹配随机功率扰动，减小动态的频率偏差，这也导致了相对较高的累计机组总运行成本。另外，部分频率偏差较大是因为微电网脱离大电网形成孤岛，缺乏大电网的支撑，其频率更容易受负荷扰动而出现较大的偏差。由附录A图A7(d)可以看出，LA仍然承担了较大的功率出力，这是由于LA具有快速响应能力，同时也由于LA补偿机制相对于DG具有一定的优势。

图3展示了全日随机扰动下各算法结果对比，与其他算法相对，EL算法获得了最小的平均频率偏差和相对较低的累计运行成本，其中平均频率偏差值计算方法见附录B。值得注意的是，PROP算法由于仅考虑固定调节因子，且一般而言具有较大备用容量的机组,其调节成本较低，因此在全日的仿真当中，PROP算法由于将功率指令按比例均分到了各机组，才使得其运行成本较低，但也导致了较差的快速爬升效果。

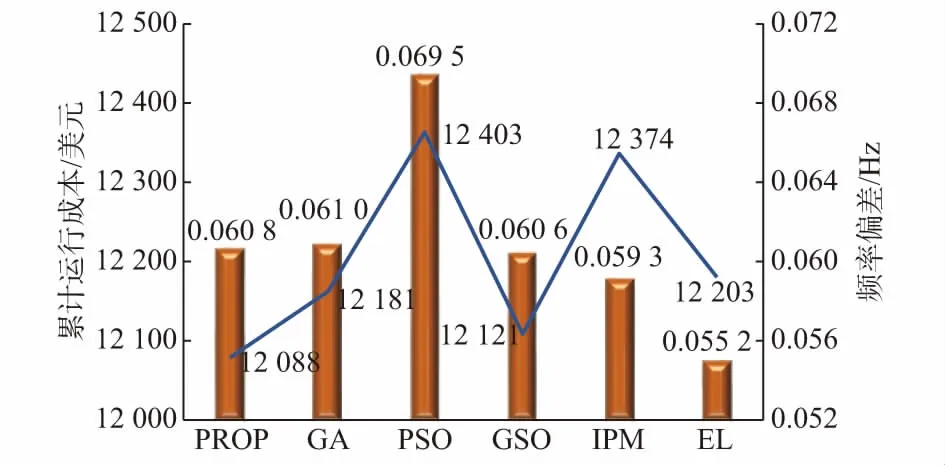
图3 不同算法全日随机功率失衡仿真结果对比Fig.3 Comparative results of different algorithms for a stochastic power disturbance over a day

5 结论

本文解决了传统DG与需求侧用户在孤岛微电网上的频率协同控制问题，其主要贡献可总结如下。

1)以LA的形式对家庭负荷进行聚合，考虑温控设备对用户舒适度影响，提出LA对负荷进行评估与分级的方法。

2)提出了基于集体智慧的EL算法，借鉴众包竞赛思想，通过解答者不同的优化机制，为学习集中器提供多样化的学习样本来获取高质量的最优解。

3) 基于知识迁移后的EL算法能快速利用源任务的最优知识矩阵来获取新任务的最优解，用来满足孤岛微电网源—荷协同频率控制的在线优化。

本文的后续工作将进一步将考虑两个方面:①探索更多的需求侧资源与需求侧参与辅助市场的补偿机制；②考虑PI控制器与功率优化分配器的协同设计研究，以减少跟踪误差。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参 考 文 献

[1] 李鹏,张玲,王伟,等.微网技术应用与分析[J].电力系统自动化,2009,33(20):109-115.

LI Peng, ZHANG Ling, WANG Wei, et al. Application and analysis of microgrid[J]. Automation of Electric Power Systems, 2009, 33(20): 109-115.

[2] BEVRANI H, HABIBI F, BABAHAJYANJ P, et al. Intelligent frequency control in an AC microgrid: online PSO-based fuzzy tuning approach[J]. IEEE Transactions on Smart Grid, 2012, 3(4): 1935-1944.

[3] 张泽宇,张孝顺,余涛.孤岛智能配电网下的快速自动发电控制机组一致性协同控制算法[J].控制理论与应用,2016,33(5):599-607.

ZHANG Zeyu, ZHANG Xiaoshun, YU Tao. Collaborative consensus algorithm for automatic generation control in an islanded smart distribution grid[J]. Control Theory and Applications, 2016, 33(5): 599-607.

[4] SENJYU T, DATTA M, YONA A, et al. A control method for small utility connected large PV system to reduce frequency deviation using a minimal-order observer[J]. IEEE Transactions on Energy Conversion, 2009, 24(2): 520-528.

[5] KIM Y S, KIM E S, MOON S I. Distributed generation control method for active power sharing and self-frequency recovery in an islanded microgrid[J]. IEEE Transactions on Power Systems, 2016, 32(1): 544-551.

[6] 高赐威,李倩玉,李扬.基于DLC的空调负荷双层优化调度和控制策略[J].中国电机工程学报,2014,34(10):1546-1555.

GAO Ciwei, LI Qianyu, LI Yang. Bi-level optimal dispatch and control strategy for air-conditioning load based on direct load control[J]. Proceedings of the CSEE, 2014, 34(10): 1546-1555.

[7] LAKSHMANAN V, MARINELLI M, HU J, et al. Provision of secondary frequency control via demand response activation on thermostatically controlled loads: solutions and experiences from Denmark[J]. Applied Energy, 2016, 173: 470-480.

[8] XU Z, OSTERGAARD J, TOGEBY M. Demand as frequency controlled reserve[J]. IEEE Transactions on Power Systems, 2013, 26(3): 1062-1071.

[9] YU X, ZHOU Q. Practical implementation of the SCADA+AGC/ED system of the Hunan power pool in the central China power network[J]. IEEE Transactions on Energy Conversion, 2002, 9(2): 250-255.

[10] 刘维烈.电力系统调频与自动发电控制[M].北京：中国电力出版社,2006.

[11] 韩传家,张孝顺,余涛,等.风险调度中引入知识迁移的细菌觅食强化学习优化算法[J].电力系统自动化,2017,41(8):69-77.DOI:10.7500/AEPS20160619004.

HAN Chuanjia, ZHANG Xiaoshun, YU Tao, et al. Optimization algorithm of reinforcement learning based knowledge transfer bacteria foraging for risk dispatch[J]. Automation of Electric Power Systems, 2017, 41(8): 69-77. DOI: 10.7500/AEPS20160619004.

[12] 瞿凯平,张孝顺,余涛,等.基于知识迁移Q学习算法的多能源系统联合优化调度[J].电力系统自动化,2017,41(15):18-25.DOI:10.7500/AEPS20170103003.

QU Kaiping, ZHANG Xiaoshun, YU Tao, et al. Knowledge transfer basedQ-learning algorithm for optimal dispatch of multi-energy system[J]. Automation of Electric Power Systems, 2017, 41(15): 18-25. DOI: 10.7500/AEPS20170103003.

[13] MOHAGHEGHI S, FANG Y, FALAHATI B. Impact of demand response on distribution system reliability[C]// Power and Energy Society General Meeting, July 24-29, San Diego, USA, 2011: 1-7.

[14] 张华一,文福拴,张璨,等.计及舒适度的家庭能源中心运行优化模型[J].电力系统自动化,2016,40(20):32-39.DOI:10.7500/AEPS20160503002.

ZHANG Huayi, WEN Fushuan, ZHANG Can, et al. Operation optimization home energy hubs considering thermal comfort[J]. Automation of Electric Power Systems, 2016, 40(20): 32-39. DOI: 10.7500/AEPS20160503002.

[15] XU Z, OSTERGAARD J, TOGEBY M. Demand as frequency controlled reserve[J]. IEEE Transactions on Power Systems, 2013, 26(3): 1062-1071.

[16] WANG J, LI Y, ZHOU Y. Interval number optimization for household load scheduling with uncertainty[J]. Energy and Buildings, 2016, 130: 613-624.

[17] CHEHREGHANI B M. Optimal operation of energy hubs in the context of smart grids[J]. American Behavioral Scientist, 2011, 55(12): 1535-1540.

[18] SHAO S, PIPATTANASOMPORN M, RAHMAN S. Development of physical-based demand response-enabled residential load models[J]. IEEE Transactions on Power Systems, 2013, 28(2): 607-614.

[19] 侯文华,郑海超.众包竞赛:一把开启集体智慧的钥匙[M].北京：科学出版社,2012.

[20] 余涛,周斌,陈家荣.基于Q学习的互联电网动态最优CPS控制[J].中国电机工程学报,2009,29(19):13-19.

YU Tao, ZHOU Bin, CHEN Jiarong. Q-learning based dynamic optimal CPS control methodology for interconnected power systems[J]. Proceedings of the CSEE, 2009, 29(19): 13-19.

[21] ZHANG X, BAO T, YU T, et al. Deep transfer Q-learning with virtual leader-follower for supply-demand Stackelberg game of smart grid[J]. Energy, 2017, 133: 348-365.

[22] CLERC M, KENNEDY J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(1): 58-73.

[23] HE S, WU Q H, SAUNDERS J R. Group search optimizer: an optimization algorithm inspired by animal searching behavior[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(5): 973-990.

[24] REINALDO B, LUIZ A, CELIBERTO J, et al. Transferring knowledge as heuristics in reinforcement learning: a case-based approach[J]. Artificial Intelligence, 2015, 226: 102-121.

[25] IBAB K. Reactive power optimization by genetic algorithm[J]. IEEE Transactions on Power Systems, 2002, 9(2): 685-692.

[26] BANSAL J C, DEEP K. A modified binary particle swarm optimization for knapsack problems[J]. Applied Mathematics and Computation, 2012, 218(22): 11042-11061.

[27] MIRJALILI S, MIRJALILI S M, YANG X S. Binary bat algorithm[J]. Neural Computing and Applications, 2014, 25(3): 663-681.

[28] MIRJALILI S. Dragonfly algorithm: a new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems[J]. Neural Computing and Applications, 2016, 27(4): 1053-1073.

[29] HOSSAM M. ZAWBAA , EID E, et al. Binary gray wolf optimization approaches for feature selection[J]. Neurocomputing, 2015, 172: 371-381.

[30] KRYNICKI K, HOULE M E, JAEN J. An efficient ant colony optimization strategy for the resolution of multi-class queries[J]. Knowledge-Based Systems, 2016, 105: 96-106.

[31] NUTKANI I U, LOH P C, WANG P, et al. Decentralized economic dispatch scheme with online power reserve for microgrids[J]. IEEE Transactions on Smart Grid, 2017, 8(1): 139-148.