考虑系统耦合性的综合能源协同优化

宋晨辉, 冯 健, 杨东升, 周博文, 齐 格

(东北大学信息科学与工程学院, 辽宁省沈阳市 110819)

0 引言

随着社会经济水平迅速发展,能源危机也在不断加剧,据统计,中国人均资源拥有量不足世界平均水平的1/2,其中70%为不可再生的化石能源,而单位国内生产总值(GDP)能耗却是世界平均水平的2.5倍[1],同时化石能源的广泛使用,也给生态环境带来了巨大压力。可再生能源技术的飞速发展与大范围推广,为解决能源和环境污染问题提供了有效途径。国家开始大力推动风能、光能等可再生清洁能源利用,但随之也带来了新能源的消纳与并网问题[2]。因此,亟需建立一种利用率高、智慧、安全、可持续的新型能源利用模式[3]。

传统的能源利用模式中,按照能源类型可将能源系统划分为电力系统、热力系统以及天然气系统,各能源系统由于物理特性区别,在系统规划设计以及运行控制中存在不同特征[4]。而将电能、热能以及天然气调度供应割裂开来的传统供用能方式,未考虑电力系统、天然气系统和热力系统间的联系,不能充分发掘各自的供能优势与潜力,降低了能源供应模式的灵活性[5]。例如热能易于存储[6],但难以实现利用时的灵活控制,同时其传输损耗较大;而电能虽然具有分布范围广,传输速度快,控制手段灵活等优势,但其即发即用,难以大容量、长时间存储的弊端却带来了电网高渗透率下的清洁能源消纳问题。因此,对电、热、气综合能源优化运行及其耦合关系进行研究,符合综合能源系统(integrated energy system,IES)运行时的多能耦合互补特征,有利于提高能源的综合利用效率。

目前,国内外学者对多能源耦合及优化运行已经做出了一定研究。文献[7]提出一种基于电力网、液压和热水回路以及耦合元件的电热网络联合分析方法,并通过一种分解集成算法降低了优化时的迭代次数;文献[8]针对大不列颠地区的风电、天然气及储能联合运营情况,提出了一种考虑天然气管网非线性特征的电、气联合优化策略,并采用随机规划对常规机组进行调度以满足风电预测的随机性;文献[9]提出了一种电、热、气多能源最优能流的解耦求解方法,通过引入多智能体对各能源进行协同优化,从而确定成本最优时的系统运行方式;文献[10]在电、热联合供能系统中引入了热电联产(combined heat and power,CHP)及热泵等单元来提高系统运行的灵活性,优化过程的同时考虑了建筑物的热惯量及用户满意度等需求侧特性;文献[11]对冷热电联供系统和热网组成的多区域IES进行了研究,通过多区域冷热电量及系统容量的协同配置,实现系统规划运行时的成本最优;文献[12]通过建立电力—天然气区域IES的稳态模型,重点研究了天然气网络状态变化对其他耦合能源系统状态的影响。

但已有的IES优化运行模型,往往在结构特征上做了简化,对电、热、气能源间的耦合性考虑不足,能源间的耦合性分析多集中于定性讨论,缺乏定量分析,进而难以准确评估系统运行时由多能耦合带来的互补效益。为此,本文构建了一种较为完备的同时耦合电力、热力以及天然气的IES,并通过能源耦合度等相关定义的建立,对IES的耦合性进行了定量描述;之后建立了以运行成本为目标的IES优化模型,针对IES运行时多能耦合特性带来的求解困难,提出一种基于拉格朗日松弛(Lagrangian relaxation,LR)的求解方法,并针对传统LR方法中收敛速度慢、迭代振荡等问题,提出了改进算法。最后,基于71节点的IES测试系统,验证了本文所述模型及方法的有效性,并对IES运行成本与耦合性的映射关系及规律做了定量分析。

1 IES结构和系统耦合性

1.1 系统结构

IES在能源的生产、消费等环节中,同时耦合了电能、热能以及天然气能等多种能源形式[13],本文所述的IES基本形态结构可由图1表示。该系统由电力系统、热力系统以及天然气系统构成。其中电力系统包括风机、火电机组、蓄热式电锅炉以及电负荷;热力系统包括CHP机组、燃气锅炉、电转气(power to gas,P2G)机组[14]、蓄热式电锅炉以及热负荷;天然气系统包括气井压缩机、CHP机组以及燃气锅炉。电力系统、热力系统和天然气系统通过蓄热式电锅炉、CHP机组、P2G机组以及燃气锅炉耦接在一起,各能量流入流出关系如图1所示,其中P,Q,G分别表示电能、热能以及天然气能。

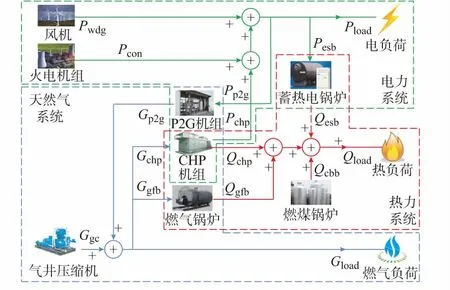
图1 IES基本形态结构Fig.1 Basic configuration structure of IES

1.2 系统耦合性

IES的电、热、气耦合关系通过系统内的供能单元建立,为具体说明系统内各能源间的耦合关系,首先给出以下定义。

定义1:能源结构配比。能源结构配比指系统运行时,供能单元的输入或输出功率的能源形式占比,用于表征某供能单元运行时,其某种能源形式的输入/输出功率对系统中该能源的依赖或影响程度。具体表示为单元αi以电能、热能以及天然气为表现形式的输入或输出能量Eαi→Ω,占其总输入或输出能量Eαi的比值,即

(1)

式中:RES，αi→Ω为αi关于Ω(Ω∈{P,Q,G,…})的能源结构配比;sαi为状态参数。

规定当Ω为αi功率输入侧的某种能源时,sαi<0;当Ω为αi功率输出侧的某种能源时,sαi>0;当Ω与αi无能源输入或输出关系时,sαi=0。

对于包含n个单元的电、热、气IES,IES为电力、热力、天然气系统的并集,其能源结构配比矩阵RES,IES为:

(2)

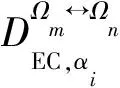
(3)

式中:RES,αi→Ωm和RES,αi→Ωn分别为单元αi关于Ωm和Ωn的能源结构配比;EIES为IES包含电、热、气的总输出能量。

考虑到单元αi的能量转化传递效率,式(3)中的Eαi统一采用αi输出侧能量值;同时,当系统中能量传输存在网络损耗及备用时,EIES需要计及传输损耗及备用能量。

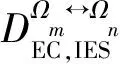
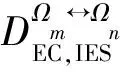
(4)

2 IES优化运行模型

2.1 目标函数

综合能源优化以系统总运行成本CIES为优化目标,系统总运行成本包括供电、供热以及供气成本。对应供能成本CP,CQ,CG可由能源结构配比矩阵与系统中单元供能成本向量的乘积逐一表示,能源耦合度可由能源结构配比及单元供能向量求得,具体表现形式如下:

(5)

(6)

式中:Nt为优化运行的总时段；Cα(t)为t时刻IES中供能单元运行成本向量。

本文基于图1所示结构,Cα可表示为:

Cα=Cwdg,1,…,Cwdg,nwdg,…,Ccon,ncon,…,

Ccbb,ncbb,…,Cchp,nchp,…,Cesb,nesb,…,

(7)

式中:Cwdg,Ccon,Ccbb,Cchp,Cesb,Cp2g,Cgfb,Cgc分别表示风机、火电机组、燃煤锅炉、CHP机组、蓄热电锅炉、P2G机组、燃气锅炉以及气井压缩机的运行成本;nwdg,ncon,ncbb,nchp,nesb,np2g,ngfb,ngc为系统中各对应单元个数。

火电机组、CHP机组、燃煤锅炉、燃气锅炉和气井压缩机的运行成本函数及参数见附录A。同时,本文采用日前调度模型对系统总供能成本进行计算,短期调度运行时,可忽略风机、蓄热电锅炉及P2G机组运行的边际成本,但需满足各自的运行约束及能源转换效率约束[15]。

2.2 约束条件

IES运行时需综合考虑各能源的电、热、天然气功率平衡、网络潮流、供能单元特性等约束条件,可按类分为系统运行约束以及系统内各供能单元的运行约束。

2.2.1系统运行约束

1)功率平衡约束

(8)

Ql，t+Qloss

(9)

(10)

式中:Pl,t,Ql,t,Gl,t分别为IES的电、热及天然气负荷需求;Ploss,Qloss,Gloss分别为系统的网损以及热能和天然气能在传输过程中的损耗。

式(8)—式(10)分别表示IES运行时的电功率平衡、热功率平衡以及天然气功率平衡约束。

2)网络运行约束

(11)

(12)

qj=Clmj(Tin,j-Tout,j)

(13)

(14)

(15)

(16)

式中:w∈j表示与j相邻的节点；Pj,t和Qj,t分别为节点j在t时刻注入的有功功率和无功功率;Uj,t和Uw,t分别为节点j和w在t时刻的电压;Gjw和Bjw分别为节点j和w间的电导和电纳;θjw,t为节点j和w之间在t时刻的相角差;As为热力网节点支路关联矩阵;Ml为管道流量向量,其元素为ml;Mj为节点流量向量,其元素为mj;Bh为热力网回路支路关联矩阵;ΔHl为管道水压降向量;qj为节点j热功率;Cl为水比热;Tin,j和Tout,j分别为热力节点j流入和流出热水的温度;Tstart,Tend,Tα分别为管道的始端、末端及环境温度;β和L分别为管道的热传导系数及长度;g∈j表示与热力节点j相连的管道；min,g和Tin,g分别为管道g流入节点的热水流量和温度;mout,g和Tout,g分别为管道g流出节点的热水流量和温度;fjw为天然气网节点j和w间的管道稳态流量;Kr为天然气管道常数;πj和πw分别为天然气网节点j和w的压力;sjw为天然气流动方向的状态参数,若πj≥πw,则sjw取1,否则sjw取-1。

式(11)—式(16)分别表示电力网潮流、热力网水网平衡、节点热功率、管道始末端温度、节点温度平衡约束[6]以及天然气网的管道流量约束[16](采用Weymouth公式形式)。

3)旋转备用约束

考虑到风电及负荷的波动性,采用火电机组作为主备用，保证二者波动时的容量备用需求,即

(17)

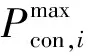
2.2.2单元运行约束

1)风机运行约束

(18)

Pw,i,t-Pwdg,i,t≤(1-rw)Pr,i

(19)

式中:Pr,i为风机i的额定功率;vci,vr,vco,v(t)分别为风机的切入风速、额定风速、切出风速以及t时刻的实际风速;a和b为风机出力特性参数;h为风机出力特征指数；Pw,i,t和Pwdg,i,t分别为风机i在t时刻的最大发电量与实发电量;rw为系统要求的风能最小利用率。

式(18)和式(19)分别为风机出力约束以及弃风量约束[17]。

2)火电机组运行约束

(20)

(21)

(22)

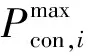
式(20)—式(22)分别表示火电机组的出力上下限约束、爬坡率约束以及开停机时间约束。

3)CHP机组运行约束

为了增加系统运行的灵活性,选用热电比可调的抽凝式CHP机组参与建模[18],机组运行时需要满足其运行工况曲线,即

(23)

(24)

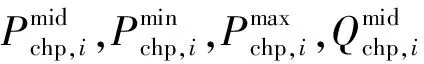
式(23)和式(24)分别表示CHP机组的有功出力上下限约束以及热出力上下限约束。

4)蓄热电锅炉、P2G机组、燃气锅炉运行约束

蓄热电锅炉、P2G机组、燃气锅炉均需满足功率转换约束、输入或输出功率约束,即

Ωα,n,i,t=ηα,iΩα,m,i,t

(25)

(26)

Ω∈{P,Q,G}

(27)

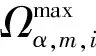
此外,蓄热电锅炉仍需满足蓄热量上限约束,即

(28)

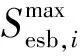
3 IES协同优化方法

3.1 求解困难分析与松弛问题构建

IES运行时,其内部电、热、气能源的耦合并存有利于发挥系统的多能互补与协同效益,但多能耦合现象却为综合能源优化求解带来了困难,传统意义上的电、热、气单一能源系统的最优运行点,往往不是IES运行的全局最优点。而由多能耦合带来的求解困难主要集中在如下两个方面。

问题1:单元αi输入、输出侧能源隶属于不同能源系统时,其输入、输出能量存在耦合,相互影响并与该单元的系统隶属度相关,如CHP机组、蓄热电锅炉、P2G机组以及燃气锅炉等。

问题2:单元αj的输出侧能源隶属于多个能源系统时,其输出能量存在耦合,相互影响并与该单元的系统隶属度相关,如CHP机组。

针对以上问题,本文采用LR方法对IES优化运行模型进行解耦处理,从而降低问题的求解难度。

问题1中的耦合问题主要体现于能量的输入、输出过程中,故本文引入拉格朗日乘子μ,λ,φ,ψ,对反映系统输入、输出关系的约束,具体包括系统功率平衡约束及旋转备用约束(式(8)—式(10)及式(17))进行松弛,可得LR问题:

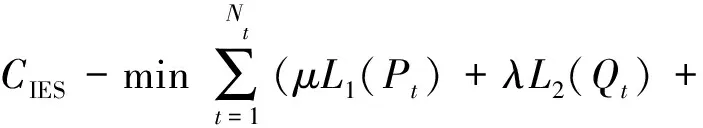
φL3(Gt)+ψL4(Pt))

(29)

式中:L1(Pt),L2(Qt),L3(Gt),L4(Pt)分别对应电、热、气功率平衡以及旋转备用约束松弛后的惩罚项。其中CHP机组、蓄热电锅炉、P2G机组以及燃气锅炉的运行成本函数通过各自的能源转换效率约束,可将由输入、输出侧能源不同导致的双变量优化问题,转换为仅与输出侧能源有关的单变量优化问题。

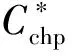
1)CHP机组运行点在运行边界上时

此情况下,可借助电—热功率弹性系数cm及机组运行的边界约束,将同时包含Pchp,i,t和Qchp,i,t的运行成本模型转化为只包含优化变量Pchp,i,t(或Qchp,i,t)的成本模型进行求解。

2)CHP机组运行点在运行边界内时

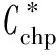
(30)

3.2 求解过程

经上述转化,原多能源优化问题可转化为无耦合的电、热、气单能源系统优化问题。而通过对偶理论,可将LR问题转化为双层优化问题:

(31)

maxPLR,down(μ,λ,φ,ψ)

(32)

对于上层单变量优化问题,本文采用基于表函数模型的近似动态规划方法进行求解[20]。在底层对偶优化问题求解时,针对传统次梯度法收敛速度慢以及局部振荡的问题,本文采用改进逐步次梯度法对对偶问题进行优化求解,主要涉及迭代步长的选取以及迭代方向的修正。

传统的次梯度法在迭代过程中只利用了当前点的次梯度方向,忽略了之前的迭代方向,逐步次梯度法认为局部最优解与全局最优解在空间上具有相似性,可以通过对信息的充分利用,即时向最优解方向逼近。乘子μ,λ,φ,ψ的更新方式如下:

(33)

(34)

(35)

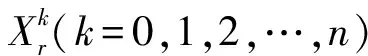
由于修正方向在一定程度上反映了优化结果对松弛约束的满意度,令修正步长借助修正方向进行自适应确定,可以更好地加速迭代的收敛过程:

(36)

4 算例分析

4.1 优化算例及场景设计

本文71节点的IES仿真算例结构见附录B图B1,其中电力系统采用改进的IEEE 39节点系统,修改PV节点35和38的电源类型为风机,节点32,37,39的电源类型为CHP机组;16节点热力系统和16节点天然气系统取自某实际示范区域。电力、热力以及天然气系统通过蓄热式电锅炉、CHP机组、P2G机组以及燃气锅炉耦合互联。电、热、天然气负荷功率及风电功率预测数据选自示范地区供暖季典型日数据,四者功率预测曲线见附录B图B2。同时,功率均采用标幺值表示,电、热、气功率的基准值分别取100 MW,100 GJ/h,1 000 m3/h。

另外,为验证本文优化方法的有效性以及耦合性对IES运行情况的影响,考虑如下3种场景。

场景1:IES中各能源耦合度均为0,此时电力、热力、天然气系统运行相互独立。

场景2:IES在弱耦合态势下运行,设置各能源间耦合度保持在10%以内,此时电力、热力、天然气系统运行可以相互影响。

场景3:IES在最优耦合态势下运行,取消各能源间的耦合度限制,电力、热力、天然气系统运行实现协同优化。

4.2 基于系统耦合性的协同优化效果分析

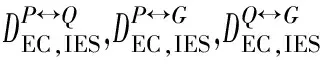
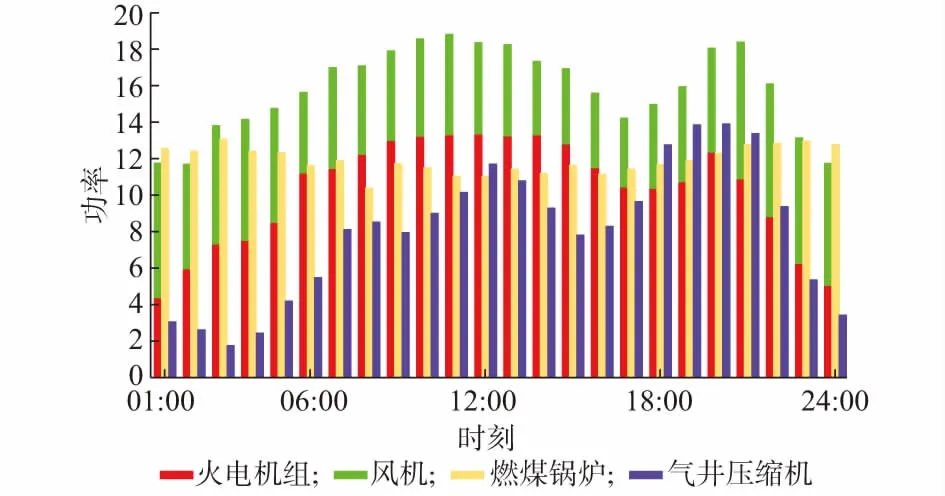
图2 场景1能源优化效果Fig.2 Energy optimization results in case 1

图3为场景2和场景3的能源优化效果,其中图3(a),(c),(e)分别表示场景2的电能、热能以及天然气能优化效果;图3(b)，(d)，(f)分别表示场景3的电能、热能以及天然气能优化效果。两种场景下的IES均存在电、热、气耦合情况,区别在于场景2对于IES运行时的电、热、气间的能源耦合度进行了DEC≤10%限制。根据定义1中的相关描述,天然气系统向CHP机组输入能量,故CHP机组在天然气系统中的功率表示为负值,同时CHP机组向电力及热力系统输出能量,故其在二者中的功率表示为正。蓄热电锅炉、P2G机组及燃气锅炉同理。

由图2及图3(a)和(b)可以看出,当系统引入耦合时,在经济运行成本最低原则的引导下,蓄热电锅炉及P2G机组可在弃风时段为风电提供更大的消纳裕量。同时,由图3(a)和(b)可以看出,当系统在最优耦合态势下运行时,风机在01:00和03:00—24:00期间均能达到满发,弃风现象进一步降低,使得CHP机组在全天的供电出力均有不同程度的下降,可以将更多由天然气系统输入的能源转化为热能,进一步提高了系统运行的经济性和灵活性。另外,在10:00—15:00,场景3中的火电机组出力情况较场景2中的火电机组出力情况更为平稳,机组的爬坡功率降低,这在实际工况中有利于延长机组的使用寿命,减少机组的维护费用。

对比图1及图3(c)和(d)可以发现,当IES存在多能源耦合时,燃煤锅炉的部分供热出力将被CHP机组、蓄热电锅炉以及燃气锅炉出力替代;并且随着各能源间耦合度的增加,电锅炉的风电消纳能力提升,其供热出力提高,而燃煤锅炉出力将进一步降低,从而降低了系统的整体煤耗量。同时,场景3中的CHP供热出力较场景2中有所上升,这是由于系统在最优耦合情况下,CHP机组输入的天然气将更多地转化为热能。

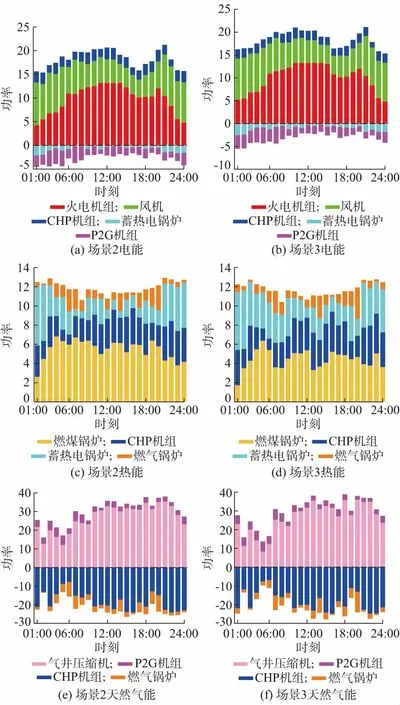
图3 场景2和3的能源优化效果Fig.3 Energy optimization results in case 2 and 3

对于天然气系统,场景1中的天然气仅由气井压缩机(气源)供应,且只需满足日常的天然气负荷(炊具、热水器等)需求。当系统存在多能源耦合时,天然气供应量有较大幅度上升。同时,在电负荷需求为谷值,而热负荷需求为峰值,如03:00—05:00时,由于蓄热电锅炉的储能效果能够实现热负荷的等效平移,故系统在该时段的燃气锅炉出力下降,进而降低了燃气锅炉的天然气耗量。而随着系统耦合性加强,受到CHP机组及燃气锅炉能耗影响,场景3较场景2中的天然气功率分布发生了一定偏移,同时气井压缩机的输出功率下降了19.06%。

表1给出了3个场景下IES运行时的各能源耦合度关系、成本以及弃风率。场景1中各能源间不存在耦合关系,此时缺乏电能存储转化单元,导致弃风量最大。在场景3中,当电—热、电—气以及热—气的耦合度分别为16.22,23.26,12.40时,IES在满足负荷需求的前提下,达到了全局最优运行,此时运行成本为668 087美元,弃风率为0.03%,两个指标均优于场景1和场景2。同时,从场景2中可以看出,当设置各能源间耦合度均需要保持在10%以内时,系统中的电—气耦合度先达到临界点,说明IES优化运行时,电、气间的耦合关系要强于电、热以及热、气间的耦合关系。

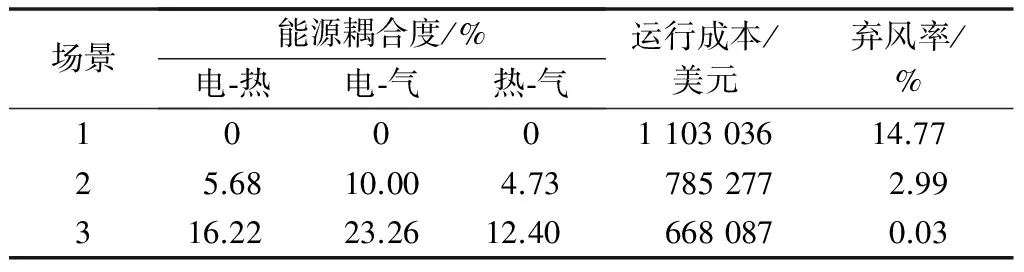
表1 不同场景下IES的能源耦合度、运行成本及弃风率Table 1 Energy coupling degrees, operation costs and wind curtailment ratios of IES in different cases

图4给出了系统能源耦合度在0～30%时,其运行成本和各能源间耦合程度的映射关系。其中,x,y,z轴分别表示电—热、电—气以及热—气的耦合度,系统运行成本大小由颜色深浅表示。

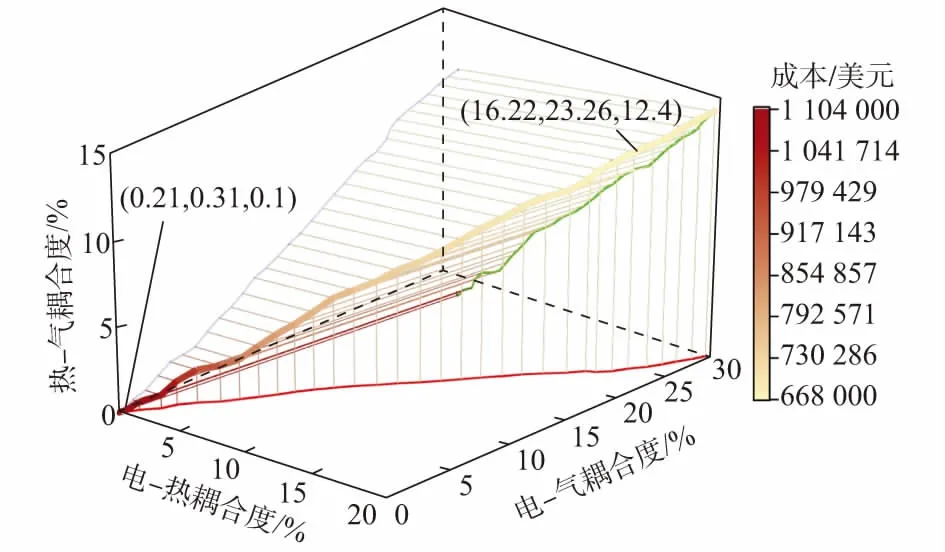
图4 系统能源耦合度与运行成本的映射曲线Fig.4 Mapping curve between energy coupling degree and operation cost of system

从图4可以看出,当系统耦合度在(0.21,0.31,0.1)～(16.22,23.26,12.4)之间时,系统运行成本随着其耦合性的增加而降低,尤其在系统耦合性增加初期,其成本节约效果最为显著;若在系统达到最优运行点时继续增加系统耦合性,会导致系统的运行成本上升,出现“过耦合”现象,原因在于此时系统已经基本不存在弃风现象,而耦合度的继续上升会使得部分单元(如火电机组)单位供能出力减小,使得其供能效率降低;同时,当耦合度为(0.21,0.31,0.1)时,系统运行成本为1 103 480美元,高于无耦合情况下的运行成本,这是由于当系统在极低的耦合态势时,虽然可以增加弃风消纳量,但却导致了CHP等单元在其较低效率的工作点运行。当系统运行点偏移最优值时,可通过系统耦合性与成本的映射关系,确定系统电—气、电—热或热—气耦合度调节量,使得系统运行点可以有效地向最优值靠近。同时,本文所述概念及方法适用于多能源联合运营区域,如在极端恶劣天气情况下,可通过电、热、气耦合关系的合理增减,避免热负荷的激增[21]对电网的安全稳定性造成影响,并同时保证系统经济运行。另外,从成本和耦合度关系曲线到各坐标面的投影情况可以看出,电—热、电—气及热—气耦合度增长呈正相关关系。

5 结语

本文首先基于电、热、天然气能源的互补特性与耦合关系,建立了IES基本形态结构,并提出了能源结构配比及能源耦合度定义,用于表征IES运行时其内部电、热、气能源的耦合关系;之后利用能源结构配比定义建立了以运行成本最优为目标的IES运行优化模型,并在建模时考虑了系统单元运行约束以及电、热、气网络约束;接着针对优化时由能源耦合带来的求解困难,提出了一种基于LR思想的求解方法,该方法可在不影响系统多能源互补效益的前提下实现能源间的解耦优化;最后,采用IEEE 39节点测试系统、16节点热力系统及16节点天然气系统构成的71节点IES网络对所述模型方法进行验证,实现了IES优化运行结果与耦合性关系的定量分析,并建立了系统耦合性与运行成本的映射关系,验证了多能耦合能够促进IES运行成本在一定区间内有效降低的结论。

IES优化运行是一个较新的研究课题,电、热、气多能耦合在降低系统运行成本的同时,也会对系统供能的安全性与可靠性造成一定影响,如何在保证系统供能经济性的前提下,利用耦合性准确分析并提高系统运行的安全性与可靠性,是下一步研究的重点。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参 考 文 献

[1] 国家统计局能源统计司.中国能源统计年鉴2016[M].北京:中国统计出版社,2016.

[2] 刘吉臻.大规模新能源电力安全高效利用基础问题[J].中国电机工程学报,2013,33(16):1-8.

LIU Jizhen. Basic issues of the utilization of large-scale renewable power with high security and efficiency[J]. Proceedings of the CSEE, 2013, 33(16): 1-8.

[3] 刘振亚.全球能源互联网[M].北京:中国电力出版社,2015.

[4] 邵成成,王锡凡,王秀丽,等.多能源系统分析规划初探[J].中国电机工程学报,2016,36(14):3817-3829.

SHAO Chengcheng, WANG Xifan, WANG Xiuli, et al. Probe into analysis and planning of multi-energy systems[J]. Proceedings of the CSEE, 2016, 36(14): 3817-3829.

[5] 贾宏杰,王丹,徐宪东,等.区域综合能源系统若干问题研究[J].电力系统自动化,2015,39(7):198-207.DOI:10.7500/AEPS20141009011.

JIA Hongjie, WANG Dan, XU Xiandong, et al. Research on some key problems related to integrated energy systems[J]. Automation of Electric Power Systems, 2015, 39(7): 198-207. DOI: 10.7500/AEPS20141009011.

[6] LU Ning, VANOUNI M. Passive energy storage using distributed electric loads with thermal storage[J]. Journal of Modern Power Systems and Clean Energy, 2013, 1(3): 264-274.

[7] LIU Xuezhi, WU Jianzhong, JENKINS N, et al. Combined analysis of electricity and heat networks[J]. Applied Energy, 2016, 162: 1238-1250.

[8] QADRDAN M, WU Jianzhong, JENKINS N, et al. Operating strategies for a GB integrated gas and electricity network considering the uncertainty in wind power forecasts[J]. IEEE Transactions on Sustainable Energy, 2014, 5(1): 128-138.

[9] MOEINI-AGHTAIE M, ABBASPOUR A, FOTUHI-FIRUZABAD M, et al. A decomposed solution to multiple-energy carriers optimal power flow[J]. IEEE Transactions on Power Systems, 2014, 29(2): 707-716.

[10] YANG Yulong, WU Kai, LONG Hongyu, et al. Integrated electricity and heating demand-side management for wind power integration in China[J]. Energy, 2014, 78: 235-246.

[11] 王珺,顾伟,陆帅,等.结合热网模型的多区域综合能源系统协同规划[J].电力系统自动化,2016,40(15):17-24.DOI:10.7500/AEPS20160426010.

WANG Jun, GU Wei, LU Shuai, et al. Coordinated planning of multi-district integrated energy system combining heating network model[J]. Automation of Electric Power Systems, 2016, 40(15): 17-24. DOI: 10.7500/AEPS20160426010.

[12] 王伟亮,王丹,贾宏杰,等.考虑天然气网络状态的电力—天然气区域综合能源系统稳态分析[J].中国电机工程学报,2017,37(5):1293-1305.

WANG Weiliang, WANG Dan, JIA Hongjie, et al. Steady state analysis of electricity-gas regional integrated energy system with consideration of NGS network status[J]. Proceedings of the CSEE, 2017, 37(5): 1293-1305.

[13] 董朝阳,赵俊华,文福拴,等.从智能电网到能源互联网:基本概念与研究框架[J].电力系统自动化,2014,38(15):1-11.DOI:10.7500/AEPS20140613007.

DONG chaoyang, ZHAO Junhua, WEN Fushuan, et al. From smart grid to Energy Internet: basic concept and research framework[J]. Automation of Electric Power Systems, 2014, 38(15): 1-11. DOI: 10.7500/AEPS20140613007.

[14] CLEGG S, MANCARELLA P. Integrated modeling and assessment of the operational impact of power-to-gas (P2G) on electrical and gas transmission networks[J]. IEEE Transactions on Sustainable Energy, 2015, 6(4): 1234-1244.

[15] 陈沼宇,王丹,贾宏杰,等.考虑P2G多源储能型微网日前最优经济调度策略研究[J].中国电机工程学报,2017,37(11):3067-3077.

CHEN Zhaoyu, WANG Dan, JIA Hongjie, et al. Research on optimal day-ahead economic dispatching strategy for microgrid considering P2G and multi-source energy storage system[J]. Proceedings of the CSEE, 2017, 37(11): 3067-3077.

[16] ABEYSEKERA M, WU J, JENKINS N, et al. Steady state analysis of gas networks with distributed injection of alternative gas[J]. Applied Energy, 2016, 164: 991-1002.

[17] 张昭遂,孙元章,李国杰,等.计及风电功率不确定性的经济调度问题求解方法[J].电力系统自动化,2011,35(22):125-130.

ZHANG Zhaosui, SUN Yuanzhang, LI Guojie, et al. A solution of economic dispatch problem considering wind power uncertainty[J]. Automation of Electric Power Systems, 2011, 35(22): 125-130.

[18] 施锦月,许健,曾博,等.基于热电比可调模式的区域综合能源系统双层优化运行[J].电网技术,2016,40(10):2959-2966.

SHI Jinyue, XU Jian, ZENG Bo, et al. A bi-level optimal operation for energy hub based on regulating heat-to-electric ratio mode[J]. Power System Technology, 2016, 40(10): 2959-2966.

[19] 陈建华,吴文传,张伯明,等.消纳大规模风电的热电联产机组滚动调度策略[J].电力系统自动化,2012,36(24):21-27.

CHEN Jianhua, WU Wenchuan, ZHANG Boming, et al. A rolling generation dispatch strategy for co-generation units accommodating large-scale wind power integration[J]. Automation of Electric Power Systems, 2012, 36(24): 21-27.

[20] 韦化,龙丹丽,黎静华.求解大规模机组组合问题的策略迭代近似动态规划[J].中国电机工程学报,2014,34(25):4420-4429.

WEI Hua, LONG Danli, LI Jinghua. Policy iteration-approximate dynamic programming for large scale unit commitment problems[J]. Proceedings of the CSEE, 2014, 34(25): 4420-4429.

[21] CORREA-POSADA C M. SNCHEZ-MARTN P, LUMBRERAS S. Security-constrained model for integrated power and natural-gas system[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(3): 326-336.