计及需求响应的主动配电网短期负荷预测

苏小林, 刘孝杰, 阎晓霞, 王穆青, 韩学楠

(1. 山西大学电力工程系, 山西省太原市 030006; 2. 国网大同供电公司, 山西省大同市 037008)

0 引言

随着用户侧各种需求响应方式的发展,大量分布式光伏、电动汽车以及储能装置等广义需求响应资源在用户侧出现[1-3]。广义需求响应资源的加入以其更加灵活多样的方式进行需求响应,使负荷转移能力增强,可转移时间范围更广。同时,售电市场的逐步开放,为各种广义需求响应资源提供了参与电力市场的条件与环境[4-6],拥有广义需求响应资源的用户将根据不同资源的出力特性,对市场的激励信号进行主动响应,实现资源的最大化利用。用户与配电网的双向互动,改变了主动配电系统的负荷特性与变化规律[7-10]。为此,在运行调度与电力市场的短期负荷预测中,需要计及需求响应,以提高预测精度。

国内外对于计及需求响应的负荷预测问题已开展了一些相关研究。文献[11]通过分析以电价为引导的需求响应对用户负荷的影响,并利用多种负荷预测方法(自回归模型、人工神经网络、递归神经网络)对不同电价模式的用户负荷进行预测,指出电价对负荷影响使传统负荷预测方法的误差明显增大,而将电价直接添加为传统预测模型的外生输入变量后,预测误差没有明显改善。文献[12]利用小波变换—神经网络方法对实时电价引导下家居响应负荷进行预测,结果指出利用小波变换对负荷数据、电价数据进行标准化处理和预分解,预测误差明显低于直接利用神经网络进行预测。文献[13]指出用户侧需求响应增大了负荷预测的不确定性,分析了负荷预测的新要求,提出并验证了负荷预测误差与电价的相关性和被影响负荷与电价的相关性的高度相似性,认为求电价与被影响负荷的关系可以转化为求电价与预测误差的关系,这为考虑电价影响的响应负荷预测提供了新的思路。文献[14]认为用户响应是按照用户代理与售电商做出的响应合约计划进行的,将用户主动响应计划作为负荷预测的外生输入量,利用不同负荷预测方法测试得出将响应计划作为输入变量能够降低负荷预测的误差,而预测精确度由建立用户响应模型的精确度决定。文献[15]通过频谱分析计及了需求响应负荷的特性,并构建了计及需求响应的Elman神经网络短期负荷预测模型,但其计及的需求响应是由系统调度员将响应信号发送给用户的,没有体现用户响应的主动性,所面向的负荷与主动配电网负荷在特性上有差异。小波分解是在傅里叶变换的基础上兴起的一种时—频局部化信号分析方法,其通过将时域上的负荷序列变换到频域上,分解为不同频率的分量,通过合理选取小波基,可以提取出适当频率的负荷分量。由小波基派生的派生小波精度可以随意变化,而且可以对局部信号进行精度的量度,相比于傅里叶分析,可以获得更多局部时间区间的信息[16-17]。在智能机器算法方面,支持向量机是建立在统计学习理论的VC维理论和结构风险最小原理基础上的,能够根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折中,以求得最好的推广能力,不敏感损失函数的引入使支持向量机可用于回归拟合问题,形成支持向量回归(SVR)方法,被认为是神经网络的替代方法[18-19]。

本文充分利用需求响应信号作为负荷预测信息,结合能够提取特定频率负荷的小波分解和高回归能力的SVR,研究在计及需求响应影响下的负荷分解算法和组合预测模型,以提高主动配电网短期负荷预测精度。

1 需求响应对负荷的影响

售电市场的开放和聚合代理的产生使整个主动配电系统的结构变成多层互动形式,同时不同层次主体的优化运行使其负荷发生改变[8]。尽管聚合代理所面向的最末端用户负荷呈现出多样化响应模式和负荷曲线,但由于广义需求响应资源中源性资源(如分布式电源)的供电作用,与传统配电网负荷相比,主动配电网的总负荷相对减少,而荷性和源荷性资源(如储能)的负荷转移功能将负荷曲线变得平稳。在由下至上不同层面的主体经过售电市场的各种信号激励而主动优化响应后,最终体现在区域主动配电网的负荷上,对负荷的影响结果是削峰填谷,主动配电网可能的日负荷曲线如附录A图A1中峰谷差较小的曲线所示。同时,在用户侧源性响应资源中,很大一部分是分布式光伏、风电,这些资源受不同日气象因素的影响,呈现出较大波动性、随机性,这将影响到电力市场中广义需求响应资源的实际响应总量,进一步使响应市场供需关系发生变化,最终导致主动配电网的不同日响应负荷曲线变得差异性较大。因此,主动配电网在不同日的负荷曲线受气象条件、市场变化等影响更加明显,周期规律性变得更差。其多日负荷曲线如附录A图A2所示。

2 计及需求响应的负荷预测思路

主动配电网的全部负荷既包括传统不可调不可控负荷,又包括广义需求响应资源的综合优化负荷,这两部分负荷的曲线特性和影响因素都是截然不同的。若一起考虑建立统一模型,难以充分、合理地计及所有影响因素,导致预测误差增大。因此,应根据负荷形成机理进行负荷分解,然后再分别预测。

聚合代理在售电市场中进行需求响应交易后,在执行需求响应计划前,需要向主动配电网运营者提交响应计划以进行技术校验,在校验完毕后下发给聚合代理,也就是说,聚合代理最终的响应行为是按照校验后的响应计划执行的,意味着主动配电网运营者对聚合代理的响应计划PDR是提前预知的。因此,这一重要信息可以用于主动配电网的负荷预测。但必须强调,受风速、云量或光照强度预测误差以及用户行为随机性的影响,聚合代理的最终响应为PDR(true)。故实际主动配电网负荷可以为:

P(t)=P0(t)+PDR(true)(t)

(1)

式中：P(t)为主动配电网负荷；P0(t)为传统配电网无响应时的负荷；PDR(true)(t)为聚合代理实际响应负荷量。

当PDR(true)(t)为正值时，代表t(t=1，2，…，24)时刻广义需求响应资源表现为荷性，使主动配电网总负荷增加；当PDR(true)(t)为负值时，代表t时刻广义需求响应资源表现为源性，使主动配电网总负荷减少。

式(1)按照形成方式不同将主动配电网负荷分为两部分，但是这两部分信息都不能直接获取，必须将其进一步分解。考虑PDR(t)是提前掌握的信息，故可以将PDR(true)(t)分为：

PDR(true)(t)=PDR(t)+r(t)

(2)

式中：r(t)为由气象因素、用户行为随机性导致的聚合代理需求响应在t时刻的误差项。

同时，传统配电网负荷在同一季节的基础负荷具有很强的规律性，因此，P0(t)也可以分为：

P0(t)=Pb(t)+R(t)

(3)

式中：Pb(t)为t时刻的季节性基础负荷；R(t)为由不同日气象因素、用户行为随机性等导致不同日负荷的波动项。

将式(2)和式(3)代入式(1)可得：

P(t)=Pb(t)+PDR(t)+r(t)+R(t)

(4)

由Pb(t)的独立性和PDR(t)的可获取性，又可将式(4)写为：

P(t)=Pb(t)+PB(t)

(5)

PB(t)=PDR(t)+r(t)+R(t)

(6)

P(t)=PDR(t)+PA(t)

(7)

PA(t)=Pb(t)+r(t)+R(t)

(8)

根据上述的分析，可以得出主动配电网的负荷预测思路流程如下。

步骤1:将主动配电网的历史负荷数据P(t)和对应时刻历史需求响应计划负荷PDR(t)代入式(7),求出周期规律较强的PA(t)。

步骤2:将多日PA(t)曲线进行波形分解,求出按日周期性规律波动的季节性基础负荷Pb(t)。

步骤3:对求得的历史Pb(t)建立适合的数学模型,并对预测日进行该部分负荷的预测。

步骤4:将主动配电网的历史负荷数据P(t)和求得的对应时刻历史Pb(t)代入式(5),求得负荷PB(t),利用PB(t)、需求响应计划PDR(t)、各气象因素之间的关系建立此部分负荷的预测模型,并对预测日该部分负荷进行预测。

步骤5:将预测日的季节性基础负荷Pb(t)和广义需求响应资源主导的部分负荷PB(t)叠加,得到主动配电网的总预测负荷P(t)。

3 计及需求响应的负荷组合预测方法

针对主动配电网负荷预测思路中的季节性基础负荷部分,由于其基本不受短期各气象因素、需求响应信号等的影响,不同日的负荷在变化趋势相同的基础上,还有一些随机过程的影响,利用时间序列模型[20]比较适合;而对于分解后的需求响应主导负荷部分,可以认为其主要是受各种外部影响因素的影响形成的。因此,可以利用回归类负荷模型,但其各影响因素的作用机制过于复杂,难以找到适合的数学模型去描述其过程,而支持向量机的自适应回归过程可以最大程度地接近各因素对负荷的影响机制,将时间序列模型与SVR模型结合进行预测,加上前面的两次负荷分解处理,形成组合预测模型。具体预测方法流程如下。

步骤1:分析预测日的日类型,根据预测日的日类型选取N天历史相似日,并提取其对应负荷数据、需求响应信号数据、温度、风速、云量等气象因素,并对各指标进行0到1的标准化处理。

步骤2:将N天历史相似日的主动配电网负荷24 h的负荷P(t)和需求响应信号PDR(t)代入式(7),求得待处理负荷PA(t),进行负荷的第1次分解,将原始负荷序列进行规律化处理。

步骤3:将求得的待处理负荷部分PA(t)进行分解,利用小波分解对其分解,取分解后的相似部分负荷CI(t)为季节性基础负荷Pb(t)作为总负荷的一部分单独进行分析预测。

步骤4:将求得的季节性基础负荷部分Pb(t)和总负荷P(t)代入式(5),求取负荷的需求响应信号及气象因素影响的负荷部分PB(t)至此完成了对主动配电网负荷的结构分解。

步骤5:利用时间序列分析模型对季节性基础负荷部分Pb(t)分析预测。包括平稳性分析、模型定阶、参数评估、模型检验、负荷预测,求得预测日季节性基础负荷Pb(t)。

步骤6:利用SVR模型对需求响应主导负荷部分进行分析预测。以N天历史日24 h的温度、云量、风速等气象因素数据,需求响应信号数据与需求响应主导负荷部分数据分别作为SVR的输入和输出数据,训练回归模型,利用训练好的模型对预测日对应部分负荷进行预测,得到预测日24 h的PB(t)数据。

步骤7:将求得的Pb(t)和PB(t)两部分对应时刻的数据进行叠加,求得预测日主动配电网总负荷P(t)。

步骤8:将求得的P(t)与预测日实际数据P0(t)比较,进行误差分析。整个主动配电网的负荷预测流程见附录A图A3。

4 算例分析

4.1 响应负荷的仿真模拟

前面所分析的组合负荷预测方法是针对未来主动配电网的,而目前中国配电侧环境与文中所述的配电系统环境还相差较远,受售电市场和用户需求响应影响的主动配电网负荷数据尚不能直接获取。为验证本文所提负荷预测方法的适用性,需对主动配电网的负荷数据进行仿真模拟。由前面的主动配电网负荷结构分析可知,未知的负荷部分为用户或聚合代理的实际响应负荷PDR(true),因为PDR(true)是由PDR信号驱动并被用户执行的,PDR(true)可由PDR的函数进行模拟。在实际情况下,用户响应随时间变化存在着内在不稳定性,响应力度受外部因素(如季节、时间点、气象条件、电价等)变化的影响。某一时刻用户实际响应负荷是由本时刻计划响应负荷的实际响应量,叠加其他各时刻计划响应负荷受影响后分摊到本时刻的响应量,而不同时刻的各外部影响因素的大小及对负荷影响机制是变化的。因此,本文构建线性时变模型如下:

PDR(true)(t)=b0(ω(t))PDR(t)+

b1(ω(t-1))PDR(t-1)+…+

bi(ω(t-i))PDR(t-i)+…+

bnb-1(ω(t-nb+1))PDR(t-nb+1)+Pr(t)

(9)

bi(ω(t-i))=bi,0+bi,1β1(ω(t-i))+

bi,2β2(ω(t-i))+bi,jβj(ω(t-i))+…+

bi,pβp(ω(t-i))

(10)

式中：Pr(t)为零均值独立恒分布随机误差部分负荷；bi(ω(t-i))PDR(t-i)为t-i时刻各外部影响因素对t-i时刻的响应计划负荷影响后，对t时刻实际响应负荷产生的影响，而bi(ω(t-i))为该部分负荷占t-i时刻响应计划负荷的百分比；ω(t-i)为在t-i时刻对用户响应产生影响的外部影响因素向量；βj(ω(t-i))为ω的函数，代表t-i时刻各外部影响因素以第j种机制影响t-i时刻的实际响应负荷；bi,p为在t-i时刻第p种影响机制的权重；i=1，2，…，nb-1；j=1，2，…，p；p为各外部影响因素对响应负荷的影响机制种类数量；nb为对t时刻实际响应负荷产生影响的连续时刻数。

同时,PDR信号也需要根据主动配电系统运营环境中可能的需求响应计划进行仿真模拟。在正常情况下,用户或聚合代理的需求响应计划不是随机形成的,而是在对其拥有的广义需求响应资源未来出力情况合理预测的基础上,根据其追求目标进行的最优响应计划。对于区域聚合负荷,PDR信号一般具有对原始负荷曲线进行削峰填谷的曲线特征,而且不同日在峰谷时段的划分上基本一致,但不同日的风速、云量、光照强度等气象因素对源性需求响应资源的出力情况影响较大。因此,尽管不同日的PDR信号在形状上相似,但其波动幅度不一致。具体波动大小可以利用主导光伏出力的云量、光照强度数据和主导风力发电的风速数据进行模拟。光照充足、风速较大,用户自身发电较多,需从电网输送的电量变少,体现在曲线上,就是削峰量增加,填谷量减少;反之则相反。

4.2 算例

本算例选用某地市城区2015年7月的负荷数据作为构成主动配电网负荷中没有进行需求响应的部分,为获取能够表现未来主动配电网负荷的负荷数据,利用4.1节中的PDR(true)模型模拟主动响应负荷部分,与未进行需求响应部分负荷叠加形成待分析的主动配电网的负荷。

为尽可能合理地进行仿真需求响应计划信号,根据各待分析日的风速、云量等综合气象数据来估计不同日的可能响应量大小。利用不同气象指标进行规范化后叠加形成综合指标,响应量线性取值范围为[-30,30]MW。其中,峰时段响应量取负值,谷时段取正值,如果用户的源性资源出力较少的话,会使峰段时间削峰较小,同时使谷段对电网的电量需求增加,即填谷增加。因此,形成的计划响应负荷信号PDR在同一日中的正值响应与负值响应的绝对值量大小互补。具体如附录A图A4中蓝色带点曲线所示。

为使模拟的PDR(true)模型信号更接近实际情况,本文使用线性时变仿真模型。取模型参数nb=3,p=1,b0,0=0.6，b0,1=0.01，b1,0=0.2，b1,1=0.01，b2,0=0.05，b2,1=0.01，外部因素的影响机制外部因素的影响机制β1(ω(t))具体如下：

(11)

将各个参数和PDR(t)代入式(9)得到模拟PDR(true)(t)负荷部分,见附录A图A4中红色星号标记的曲线。叠加上原始未计及需求响应负荷部分便得到主动配电网的全部负荷,如图1中红色峰谷差小的曲线所示,蓝色峰谷差大的曲线为原始传统配电网无需求响应负荷曲线。

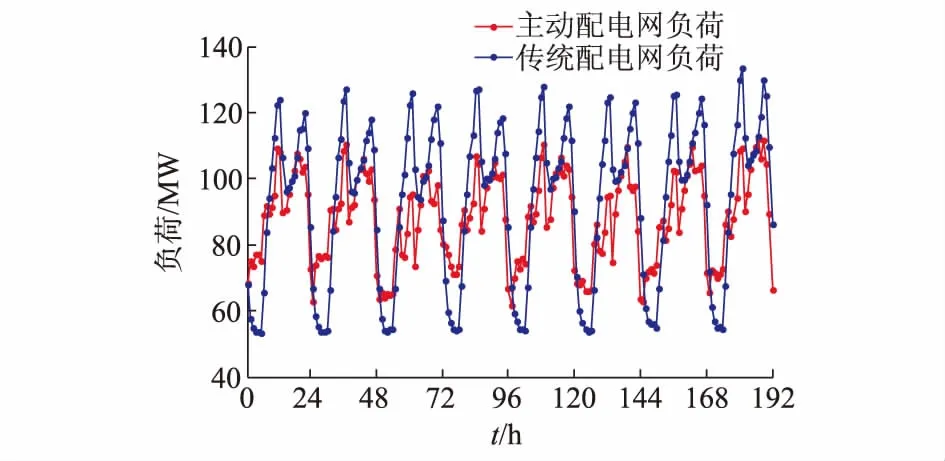
图1 传统配电网负荷与仿真的主动配电网负荷Fig.1 Load of traditional distribution network and simulative load of active distribution network

选取2015年7月27日作为主动配电网的负荷预测日,以7月中27日之前的日负荷作为负荷预测模型回归训练样本数据。为证明本文所提预测思路方法的合理性与预测效果,本文采用了以下几种模型进行预测与比较:①时间序列模型;②不计及PDR的神经网络;③不计及PDR的SVR;④计及PDR的神经网络;⑤计及PDR的SVR;⑥计及PDR和负荷小波分解的神经网络;⑦计及PDR和负荷小波分解的SVR(本文所提方法)。

4.2.1传统预测方法

利用不计及PDR的SVR模型对7月27日负荷进行负荷预测,选取与7月27日类型相同或接近的日期作为模型训练样本,模型以包括每日温度数据T(t)、湿度数据S(t)、风速数据F(t)、时刻t作为输入数据标签,以对应负荷数据P(t),预测过程在MATLAB 2013a上实现。

训练样本的实际值见附录A图A5中蓝色曲线,红色星号标记的曲线为不计及PDR的SVR模型训练后的拟合值,预测曲线与预测误差曲线如附录A图A6所示。由图A5和图A6可知,不管是训练集还是预测集,不计及PDR的SVR模型尽管都能够拟合或预测出曲线的整体变化趋势,但都没能够捕捉到主动配电网负荷曲线的波动性特征,导致预测误差较大。

4.2.2所提预测方法

1)需求响应信号预分解和小波分解

利用本文所提方法对模拟仿真的主动配电网7月27日负荷进行预测。首先利用需求响应计划信号PDR(t)(根据式(7))对训练集P(t)进行预分解得到待处理负荷PA(t),其曲线如图2(a)所示。可以看出其波动情况和传统配电网的负荷曲线基本一致,但其却混合了PDR(t)与PDR(true)(t)相差的那一部分负荷,使其曲线增加了一些细微波动。

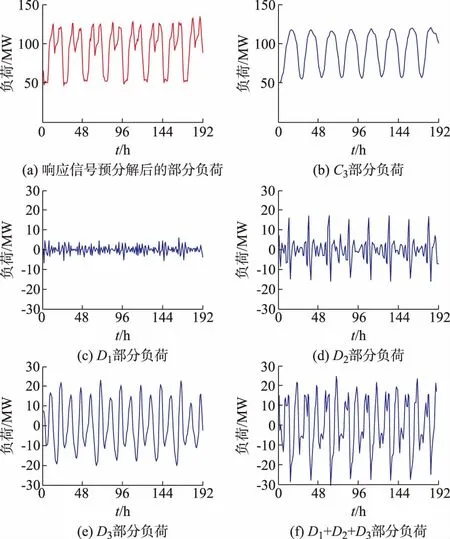
图2 待处理负荷的小波分解结果Fig.2 Small wave decomposition results of processing load

为提取出规律波动的季节性基础负荷,利用db5小波基对PA(t)进行三层分解,提取出近似部分C3和三个细节D1,D2,D3部分,如图2(b)至(e)所示。图2(f)为D1,D2,D3部分的和。其中C3部分作为季节性基础负荷Pb(t),应用时间序列模型进行分析预测。分解得到的需求响应主导负荷PB(t)曲线如图3所示。

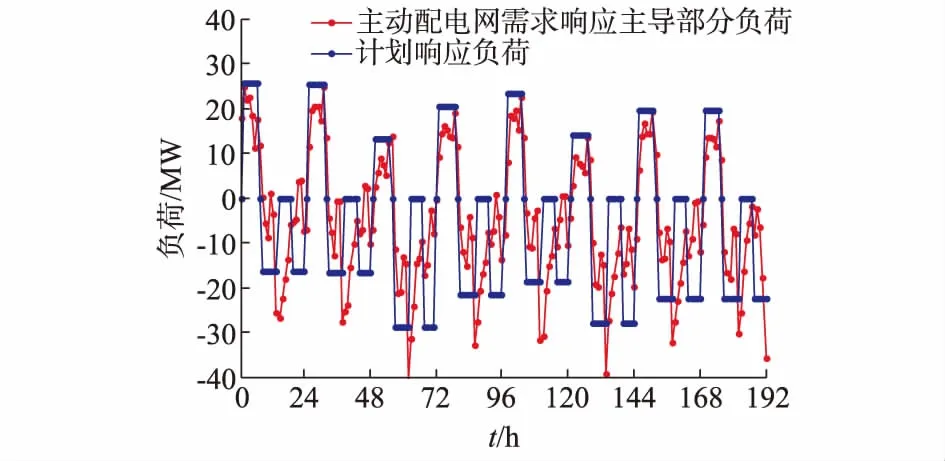
图3 需求响应主导的部分负荷与计划响应负荷Fig.3 Partial load and planned response load dominated by active demand response

利用以PDR作为输入数据之一的SVR进行预测。由于需求响应主导部分负荷除了受需求响应信号影响外,还受日周期影响因素对用户负荷在季节性基础负荷上的影响作用,因此,由图3可以看出,PB(t)与PDR(t)相比,在白天的负荷波动规律相差较大。

2)季节性基础负荷的时间序列分析预测

对于利用时间序列模型预测季节性基础负荷Pb(t),本文应用计量经济学软件EViews 8.0来实现,对Pb(t)时间序列数据进行单位根平稳检验,结果显示训练样本的t统计量的值为-7.793 283,均小于三个临界水平的值,因此可以认为所分析序列是平稳的。

对Pb(t)时间序列进行自相关、偏相关分析模型定阶,结果见附录A图A7。由图A7中可以看出,自相关和偏相关都是呈振荡型衰减趋于零的趋势,同时,自相关的波动周期为24,很久才趋于零,而偏相关在5阶后开始明显趋于零,因此模型定位为ARMA(24,5)。经过修改模型的阶数,对多组适用的模型进行赤池信息准则(AIC)与施瓦茨准则(SC)选择,发现最优模型ARMA(24,5)的AIC和SC都是最小的。利用该模型进行预测,预测结果见附录A图A8。可以看出，该模型显示出很高的预测精度。

3)需求响应主导负荷的SVR预测

利用计及PDR的SVR模型对7月27日负荷进行负荷预测,选取与7月27日类型相同或接近的日期作为模型训练样本,模型以包括每日需求响应信号PDR(t)、温度数据T(t)、湿度数据S(t)、风速数据F(t)、时刻t作为输入数据标签,以对应负荷数据PB(t)为模型输出数据。

计及PDR的 SVR模型的训练集拟合效果如附录A图A9所示。可以看出，该模型能够很好地捕捉到曲线在不同日的细节波动,有较强的适应能力。预测效果如附录A图A10所示。从图A10中可以得知,预测曲线的波动与实际负荷曲线的波动有较高的吻合度,表现出良好的预测能力。

将季节性基础负荷预测结果与需求响应主导负荷的预测结果叠加形成最终的主动配电网的负荷预测结果,预测效果及预测误差如图4所示。

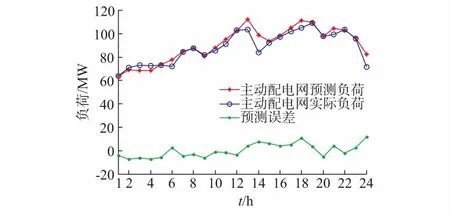
图4 本文所提方法对主动配电网负荷的预测效果Fig.4 Prediction effect of load in active distribution network by proposed method

与前面传统预测方法的预测结果(见附录A图A6)对比,图4中的预测曲线与实际负荷曲线更接近,波动吻合度高,预测误差曲线更接近于零值。

4.2.3所提预测方法与传统预测方法的对比

为更加清晰地体现本文所提预测方法的预测效果,同时为避免上述预测日可能的特殊性,本文采用多种预测模型与算法对7月27日、28日、29日进行负荷预测,将各模型拟合与预测结果的均方误差(MSE)、拟合优度(R2)及平均相对误差(δ)的参数值取平均值并进行对比,比较结果如表1所示。

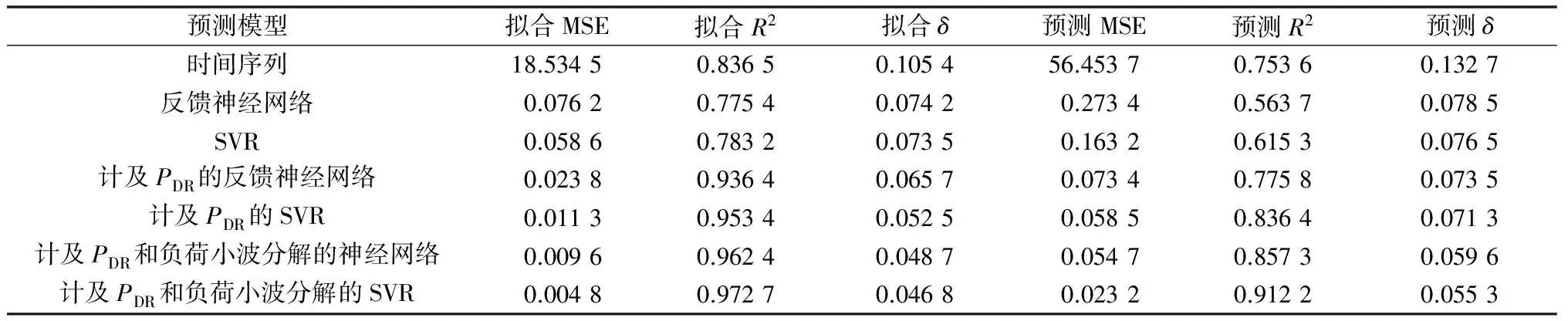
表1 各预测模型的对比Table 1 Comparison of prediction models

由表1可以看出:在不计及PDR时,经典的时间序列模型能够捕捉到日内的变化趋势,但对不同日曲线的整体变化却难以捕捉,导致预测误差很大,拟合优度却较高;而智能预测模型有输入数据标签的引导,使预测误差较低的同时,使模型拟合优度提高。另一方面,计及PDR信号时,其作为新的模型输入量使两种智能预测模型的拟合与预测效果都有大幅改善;而利用PDR信号的预分解和小波分解使模型的预测能力进一步提高。在同样情况下,SVR都比反向传播(BP)神经网络的预测效果更好。

5 结语

本文依据在主动配电系统中运营者能够提前掌握用户的需求响应计划信息这一特征,提出了计及需求响应的主动配电网组合负荷预测思路,根据主动配电网负荷的形成机制,对其组成部分进行剖析并利用需求响应计划信息进行了预分解及进一步的小波分解,最终将总负荷分为季节性基础负荷部分和需求响应主导负荷部分。根据两部分负荷的特点及规律,分别利用时间序列分析模型和SVR模型进行分析预测。经仿真模拟算例验证,本文所提方法计及需求响应信息和负荷分解再预测,相比于传统负荷预测方法,在预测误差和模型拟合优度都有所提高。

但目前主动配电系统在中国的发展处于起步阶段,文中所描述的主动配电网负荷还未形成规模,因此,未来主动配电网负荷特征可能与文中仿真的主动配电网负荷有一定的差别,可能出现本文没有考虑到的因素。在未来主动配电系统形成一定规模时,可根据真实的负荷数据进行特征分析,进而对负荷预测模型进行相应的改进。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参 考 文 献

[1] 蒋松含,张沛超,张宇,等.集成大规模需求响应资源的智能电网数字实时协同仿真方法[J].电力系统自动化,2017,41(9):130-136.DOI:10.7500/AEPS20161115004.

JIANG Songhan, ZHANG Peichao, ZHANG Yu, et al. Digital real-time co-simulation method of smart grid for integrating large-scale demand response resources[J]. Automation of Electric Power Systems, 2017, 41(9): 130-136. DOI: 10.7500/AEPS20161115004.

[2] 刘念,王程,雷金勇.市场模式下光伏用户群的电能共享与需求响应模型[J].电力系统自动化,2016,40(16):49-55.DOI:10.7500/AEPS20160120002.

LIU Nian, WANG Cheng, LEI Jinyong. Power energy sharing and demand response model for photovoltaic prosumer cluster under market environment[J]. Automation of Electric Power Systems, 2016, 40(16): 49-55. DOI: 10.7500/AEPS20160120002.

[3] 汤庆峰,刘念,张建华.计及广义需求侧资源的用户侧自动响应机理与关键问题[J].电力系统保护与控制,2014,42(24):138-147.

TANG Qingfeng, LIU Nian, ZHANG Jianhua. Theory and key problems for automated demand response of user side considering generalized demand side resources[J]. Power System Protection and Control, 2014, 42(24): 138-147.

[4] 胡晨,杜松怀,苏娟,等.新电改背景下我国售电公司的购售电途径与经营模式探讨[J].电网技术,2016,40(11):3293-3299.

HU Chen, DU Songhuai, SU Juan, et al. Preliminary research of trading approach and management modes of Chinese electricity retail companies under new electricity market reform[J]. Power System Technology, 2016, 40(11): 3293-3299.

[5] 白杨,谢乐,夏清,等.中国推进售电侧市场化的制度设计与建议[J].电力系统自动化,2015,39(14):1-7.DOI:10.7500/AEPS20150514003.

BAI Yang, XIE Le, XIA Qing, et al. Institutional design of Chinese retail electricity market reform and related suggestions[J]. Automation of Electric Power Systems, 2015, 39(14): 1-7. DOI: 10.7500/AEPS20150514003.

[6] 任艺,周明,李庚银.考虑用户需求响应的售电公司购售电决策双层模型[J].电力系统自动化,2017,41(14):30-36.DOI:10.7500/AEPS20170219003.

REN Yi, ZHOU Ming, LI Gengyin. Bi-level model of electricity procurement and sale strategies for electricity retailers considering users’ demand response[J]. Automation of Electric Power Systems, 2017, 41(14): 30-36. DOI: 10.7500/AEPS20170219003.

[7] PAOLETTI S, GARULLI A, VICINO A. Electric load forecasting in the presence of active demand[C]// Proceedings of 51st IEEE Conference on Decision Control, December 10-13, 2012, Maui, USA: 2395-2400.

[8] 刘孝杰,苏小林,阎晓霞,等.面向需求响应和售电市场的主动配电系统运营体系[J].中国电力,2017,50(7):42-50.

LIU Xiaojie, SU Xiaolin, YAN Xiaoxia, et al. Research on operation system of active distribution system in terms of active demand and sale market[J]. Electric Power, 2017, 50(7): 42-50.

[9] 罗纯坚,李姚旺,许汉平,等.需求响应不确定性对日前优化调度的影响分析[J].电力系统自动化,2017,41(5):22-29.DOI:10.7500/AEPS20160702006.

LUO Chunjian, LI Yaowang, XU Hanping, et al. Influence of demand response uncertainty on day-ahead optimization dispatching[J]. Automation of Electric Power Systems, 2017, 41(5): 22-29. DOI: 10.7500/AEPS20160702006.

[10] HONG T, WANG P. On the impact of demand response: load shedding, energy conservation, and further implications to load forecasting[C]// Proceedings of IEEE Power Energy Society General Meeting, July 22-26, 2012, San Diego, USA: 1-3.

[11] WARWEG O, ARNOLDT A, TROITZSCH C, et al. Analysis of the effects of demand response to the integration of renewable energy into the distribution grid[C]// 1st International Workshop on Integration of Solar Power into Power Systems, October 24, 2011, Aarhus, Denmark.

[12] PATERAKIS N G, CATALAO J P S, TASCIKARAOGLU A, et al. Demand response driven load pattern elasticity analysis for smart households[C]// IEEE 5th International Conference on Power Engineering, Energy and Electrical Drives, May 11-13, 2015, Riga, Latvia: 399-404.

[13] KLAIBER S, BRETSCHNEIDER P, WACZOWICZ S, et al. A contribution load forecast of price elastic consumption behaviour[C]// 2015 IEEE Eindhoven PowerTech, June 29-July 2, 2015, Eindhoven, Netherlands: 1-6.

[14] GARULLI A, PAOLETTI S, VICINO A. Models and techniques for electric load forecasting in the presence of demand response[J]. IEEE Transactions on Control Systems Technology, 2015, 23(3): 1087-1097.

[15] 于道林,张智晟,韩少晓,等.计及需求响应的Elman-NN短期负荷预测模型研究[J].电工电能新技术,2017,36(4):59-65.

YU Daolin, ZHANG Zhisheng, HAN Shaoxiao, et al. Study of short-term load forecasting model based on Elman-NN considering demand response[J]. Advanced Technology of Electrical Engineering and Energy, 2017, 36(4): 59-65.

[16] 王宁,谢敏,邓佳梁,等.基于支持向量机回归组合模型的中长期降温负荷预测[J].电力系统保护与控制,2016,44(3):92-97.

WANG Ning, XIE Min, DENG Jialiang, et al. Mid-long term temperature-lowering load forecasting based on combination of support vector machine and multiple regression[J]. Power System Protection and Control, 2016, 44(3): 92-97.

[17] 吴倩红,高军,侯广松,等.实现影响因素多源异构融合的短期负荷预测支持向量机算法[J].电力系统自动化,2016,40(15):67-72.DOI:10.7500/AEPS20160229012.

WU Qianhong, GAO Jun, HOU Guangsong, et al. Short-term load forecasting support vector machine algorithm based on multi-source heterogeneous fusion of load factors[J]. Automation of Electric Power Systems, 2016, 40(15): 67-72. DOI: 10.7500/AEPS20160229012.

[18] 王东风,王富强,牛成林.小波分解层数及其组合分量对短期风速多步预测的影响分析[J].电力系统保护与控制,2014,42(8):82-89.

WANG Dongfeng, WANG Fuqiang, NIU Chenglin. Analysis of wavelet decomposition for multi-step prediction of short-term wind speed[J]. Power System Protection and Control, 2014, 42(8): 82-89.

[19] 吴杰,丁明.采用自适应小波包分解的混合储能平抑风电波动控制策略[J].电力系统自动化,2017,41(3):7-12.DOI:10.7500/AEPS20160607009.

WU Jie, DING Ming. Wind power fluctuation smoothing strategy of hybrid energy storage system using self-adaptive wavelet packet decomposition[J]. Automation of Electric Power Systems, 2017, 41(3): 7-12. DOI: 10.7500/AEPS20160607009.

[20] 李驰,刘纯,黄越辉.基于波动特性的风电出力时间序列建模方法研究[J].电网技术,2015,39(1):208-214.

LI Chi, LIU Chun, HUANG Yuehui. Study on the modeling method of wind power time series based on fluctuation characteristic[J]. Power System Technology, 2015, 39(1): 208-214.