逆变器潮流计算节点类型等效及鲁棒下垂节点的潮流计算

肖 凡, 张昌华, 段 雪, 陈 昕, 陈树恒, 刘群英

(1. 电子科技大学机械与电气工程学院, 四川省成都市 611731; 2. 重庆邮电大学自动化学院, 重庆市 400065)

0 引言

分布式发电以其能源利用率高、污染小等特点,对于节约资源、保护环境、调整能源结构具有重要意义。但一般情况下,分布式发电利用的新能源出力往往具有随机性、不可控性,直接并入电网运行会对系统的安全性、稳定性造成不利影响。微电网作为一种将新能源、负荷、储能整合在一起,以“良好公民”的形式并网的能源利用方式,受到了国内外学者的关注[1-2]。

作为微电网中微源并网发电的重要接口,逆变器直接影响着微电网分析、管理和运行控制。从结构上来看,逆变器可以分为直流电压变换环节、电力电子开关器件、LC/LCL滤波电路以及控制算法4个部分[3]。滤波器方面,文献[4]从工程实践角度对逆变器进行建模分析,详细分析了滤波器参数的设计步骤以及限制条件。文献[5]提出了一种基于电感电压反馈和输入整形技术的LC滤波器混合阻尼控制机制,在控制系统存在扰动的情况下,可有效抑制电流波形畸变和振荡。在控制策略方面,当前主流思路是模拟传统电网同步发电机的外特性。如早期利用比例—积分(PI)控制器等将逆变器端口外特性控制成PQ/PV/Vf等特性。近年来,为适应微电网更为复杂的运行环境,出现了一批能够参与系统调频、调压管理的控制策略,如下垂控制[6-7]、鲁棒下垂控制[8]、虚拟同步发电机(virtual synchronous generator,VSG)[9]等,以及在此基础上的各种改进型控制算法。逆变器领域的这些研究,极大地促进了微电网的发展。

潮流计算是进行电力系统状态分析、稳定性评价和优化管理的前提[10]。微电网潮流计算存在分布式电源节点类型的等效问题。文献[11]借鉴传统输电网中的潮流计算模型和算法,将分布式电源分为PQ和PV类型节点,利用前推回代法计算潮流。文献[12]建立了多种分布式电源的数学模型,提出了一种基于灵敏度补偿的算法。但文献[11-12]均没有考虑下垂控制。文献[13]研究了包含下垂节点类型的微电网潮流计算问题,但文献[13]中没有讨论逆变器下垂控制策略与下垂节点类型等效之间的联系。逆变器等效节点类型与其控制策略之间的关系仍是一个需要厘清的问题。同时,对于鲁棒下垂控制等效为新型的节点类型缺乏相应的潮流求解算法研究。

基于此,本文从潮流计算节点类型等效的角度对比分析了典型逆变器控制策略,总结了适宜进行节点类型等效的逆变器控制器的特点。同时,针对鲁棒下垂控制策略,在将其等效为P(ω)-Q(V)节点的基础上,以牛顿—拉夫逊法为基础,提出了一种统一迭代的潮流算法。并以欧盟20节点微电网为例,验证了潮流算法的有效性和可行性。潮流计算的结果表明,鲁棒下垂控制器参数选取对微电网潮流分布有明显的影响。

1 微电网逆变器常规控制策略及节点类型等效分析

1.1 微电网逆变器运行环境与控制策略

鉴于LCL滤波器容易引起谐振,这里滤波电路考虑LC模式。图1为逆变器连接到微电网母线的通用结构图,包括电力电子单元、LC滤波器单元、控制算法单元和物理连线阻抗单元[14]。

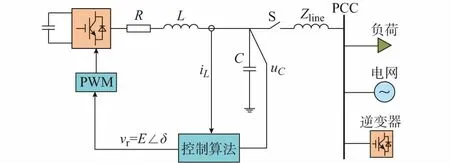
图1 微电网运行结构Fig.1 Operation structure of microgrid

图1中uC为电容两端电压,iL为逆变器侧电感电流,Zline为逆变器的物理连线阻抗单元,vr为逆变器的脉宽调制(PWM)驱动信号。在公共耦合点(PCC)处,还接有负荷、电网或其他微电网逆变器。

逆变器通过检测机端电压uC和输出电流iL,获取频率、电压幅值、输出功率等信息,进而通过不同的控制策略产生调制波vr,实现分布式电源的并网发电。

围绕调制波幅值E、相位δ和频率的产生方式,从潮流计算节点类型等效的角度,表1对当前主要逆变器控制策略的控制器特点和节点类型等效情况进行了分析[15-16]。

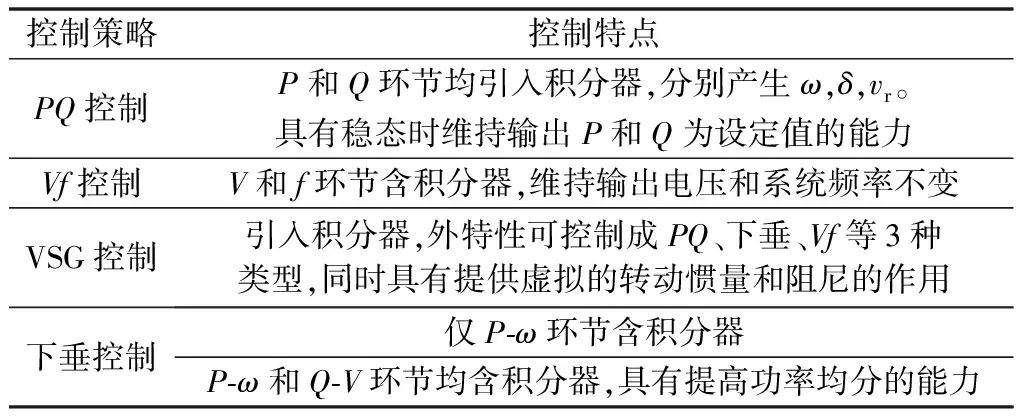
表1 逆变器控制策略及其特点Table 1 Control strategies of inverters and their characteristics

由表1可知,下垂控制分为两类:一类为传统下垂控制,即仅P-ω环节含积分器;另一类下垂控制的P-ω和Q-V环节均含积分器[17]。从潮流计算的角度来看,逆变器采取PQ,Vf,VSG控制策略,使得分布式电源等同于传统潮流计算中的PQ和Vf节点。无论在潮流计算建模还是算法上,均与传统算法保持一致。为区别起见,遵从提出该控制策略文献中的命名方式,Q-V环节无积分器的在本文中依然称之为下垂控制[7];而Q-V环节引入了积分器的称之为鲁棒下垂控制[8]。下面,将对下垂控制和鲁棒下垂控制策略进行比较研究,由此得出适宜潮流计算的节点类型等效逆变器的控制策略特点。

1.2 下垂控制

下垂控制是模拟同步发电机组外特性的控制策略,能够根据系统频率和有功功率、输出端电压和无功功率之间的关系进行二次调频和无功调节。下垂控制自提出以后,有多种实现方式,图2给出了一类不含积分器的下垂控制框图[6-7](以逆变器输出阻抗为感性为例)。

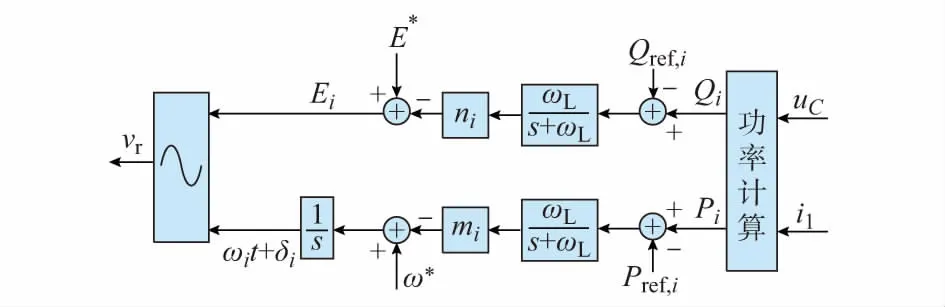
图2 下垂控制框图Fig.2 Block diagram of droop control

下垂控制部分用数学公式表示如下:

Ei=E*-ni(Qi-Qref，i)

(1)

ωi=ω*-mi(Pi-Pref,i)

(2)

式中:E*和ω*分别为逆变器空载输出的电压有效值和角频率;Ei为调制波vr的幅值;ωi为调制波的频率;mi和ni为下垂控制系数;Pi和Qi分别为逆变器输出的有功功率和无功功率;Pref,i和Qref,i分别为逆变器的有功功率和无功功率参考值。

根据图2和式(1)、式(2)可见,逆变器下垂控制实则为根据端电压幅值和输出功率,依照线性下垂的关系控制调制波vr参与系统的调压调频管理。但从图1可见,调制波vr和逆变器端部的输出之间,还有一段LC滤波器的电路,影响了逆变器实际注入电网的功率。

附录A图A1给出了稳态时从电力电子开关桥路到逆变器端口的稳压电路。易知,电容处逆变器输出的有功功率和无功功率分别如下:

(3)

(4)

式中:XL为滤波电感L的感抗值;VC为逆变器输出电压uC的有效值。

将式(1)代入式(4)。考虑到滤波电感的阻值R极小,且电感L两端的相角差δ≈0°。故忽略R,并令cosδ=1,由式(1)和式(4)可计算出VC:

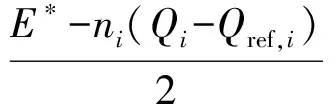
(5)

式(5)对Qi求导,可得:

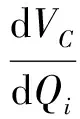
(6)

式(6)表明,即使下垂控制给出的下垂系数为ni,但最终的端电压与无功功率之间的关系受控制参数(ni,E*,Qref,i)、电路参数XL和运行状态Qi共同决定,并非简单的线性下垂关系。这导致在潮流计算中,缺乏对应的节点类型。此外,从式(6)可见,若XL相对于其他项极小,则可推出:

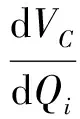
(7)

此时,VC与Qi之间才满足下垂关系。参考国内外相关文献[17-20],低压微电网系统中常见的功率和电压等级逆变器的滤波器参数如附录A表A1所示。同时根据文献[21]给出了欧盟微电网的结构和参数,附录A表A2以此为例,给出了以平均线路长度和平均阻抗所描述的线路参数。

对比附录A表A2与表A1,低压微电网系统中线路阻抗值小于滤波器的阻抗值至少一个数量级。相比于输电线路,滤波器的参数并不是足够小,无法满足式(7)成立的条件。若简单地认为下垂控制的无功功率和电压满足式(7)的下垂关系,潮流计算就会产生错误的结果。在3.1节,本文会给出一个算例,定量分析XL对逆变器输出电压和无功功率的影响。

1.3 鲁棒下垂控制

鲁棒下垂控制是近10年由英国谢菲尔德大学的钟庆昌教授提出的一种下垂控制策略[8]。相比于图2,它在P-ω环节是一样的,但在Q-V环节引入一个积分器,提高了逆变器功率均分的能力和输出电压的鲁棒性,同时也增强了系统抗扰动的能力。具体控制框图可见图3,其中Ke为放大系数。

对比图2和图3,可以列写稳态逆变器端电压和无功功率之间的方程:

(8)

其有功功率和频率的关系如下:

(9)

和下垂控制器的式(1)和式(2)比较可见,稳态的时候,式(8)和式(9)送入积分器的量等于0。因此,鲁棒下垂控制的逆变器,稳态时能够确保端口电压和输出无功功率满足特定的线性关系。这个特点有利于微电网潮流计算。

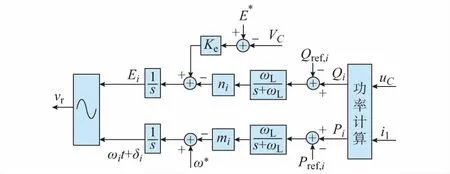
图3 鲁棒下垂控制框图Fig.3 Block diagram of robust droop control

1.4 逆变器节点等效为现有潮流节点类型的条件

通过上面的分析可见,可以从是否适应当前潮流计算算法的角度,考虑把逆变器的控制策略分为两类。一类为诸如Q-V环节不含积分器的下垂控制和以下垂方式运行的VSG控制[22]。其特点是控制器缺乏积分器环节(一般为Q-V环节)。若在低压微电网的潮流计算中忽略滤波器的参数进行节点类型等效,有可能产生错误的结果。而另一类为诸如PQ控制、Vf控制、VSG控制(以PQ/PV/Vf的方式运行)、带PI环的下垂控制和鲁棒下垂控制。其特点是产生调制波的幅值、频率和相位环节均含积分器。稳态时,积分器的输入必然为0,这就保证了逆变器的输出功率、电压幅值、频率之间满足特定的关系。后面这一类适合进行节点类型等效。

此外,从式(8)和式(9)可见,鲁棒下垂控制的逆变器在潮流计算节点等效中属于一种P(ω)-Q(V)节点类型[13],是一种不同于PQ和PV类型节点的新型节点。

2 鲁棒下垂控制逆变器的微电网潮流计算

潮流计算的实质是求解非线性代数方程组[23]。鉴于牛顿—拉夫逊法的二阶收敛特性,本文以牛顿—拉夫逊法为基础,引入鲁棒下垂节点的Q-V和P-ω控制方程,构建以电压为初值的逆变器节点的修正方程,以适应此类微电网的潮流计算。其他如PQ/PV/Vf控制策略节点类型的处理方法和现有文献一致,在此不再赘述。

2.1 传统节点类型的修正方程

对交流母线i,其节点电压方程和导纳矩阵元素为[23]:

(10)

式中:ei和fi分别为电压相量的实部和虚部;Gij和Bij分别为导纳矩阵元素的实部和虚部。

功率方程:

(11)

将式(10)代入式(11)的右端,展开并分出实部和虚部,得:

(12)

对于PQ节点,其有功功率和无功功率是给定的,第i个节点的给定有功功率和无功功率设为Ps,i和Qs,i。

假定系统中的第1,2,…,l个节点为PQ节点,对其中每一个节点可列方程如下:

(13)

式中:i=1,2,…,l。

对于PV节点,其有功功率和节点电压幅值是给定的。假定系统中第l+1,l+2,…,m个节点为PV节点,则对其中每一节点可以列写方程如下:

(14)

式中:i=l+1,l+2,…,m。

2.2 鲁棒下垂节点的修正方程

而对于鲁棒下垂控制逆变器节点,式(8)和式(9)引入了一个输出有功功率和频率之间、无功功率和电压之间的新的约束关系。假定系统中第m+1,m+2…,n-1个节点为鲁棒下垂节点。稳态时,P-ω约束方程为:

mn(Pn-Pref,n)=Δω=mi(Pi-Pref,i)

(15)

式中:Δω为系统频率变化量;Pref,n为平衡节点的有功功率参考值。

Q-V约束方程:

Ke(E*-VC)-ni(Qi-Qref,i)=0

(16)

由此得鲁棒下垂节点的修正方程为:

(17)

式中:ΔPDi和ΔQDi分别为鲁棒下垂节点中有功功率和无功功率的不平衡量;i=m+1,m+2,…,n-1。

2.3 潮流计算中逆变器功率越限的处理

假定逆变器输出无功功率上限为Qmax,i,输出无功功率下限为Qmin,i。若其输出无功功率越限,且其越限后的无功功率为Qlimit,i,则鲁棒下垂逆变器节点转换为P(ω)-Q节点类型。其相应的修正方程为:

(18)

假定逆变器输出有功功率上限为Pmax,i,输出有功功率下限为Pmin,i。若其输出有功功率越限,且其越限后的有功功率为Plimit,i,则鲁棒下垂逆变器节点转换为P-Q(V)类型节点。其相应的修正方程为:

(19)

当然,若P和Q均越限,则转换为PQ节点,表达式如式(13)所示。

2.4 潮流计算中平衡节点的处理

潮流计算中的平衡节点一般为微电网与大电网并网的节点,在潮流计算中起功率松弛和提供频率支撑的作用。在微电网孤岛模式下,本文假定其中一个容量较大的逆变器充当平衡节点。观察式(8),若令ni=0,即可解除Q-V约束。此节点即可选定为平衡节点。第n号节点为平衡节点,电压方程为:

(20)

由于平衡节点电压为给定值,故不参与迭代。

2.5 求解方法

式(13)、式(14)和式(17)共包含了2(n-1)个方程,待求量e1,f1,e2,f2,…,en-1,fn-1也是2(n-1)个。将其写成牛顿—拉夫逊法的矩阵向量形式如下:

(21)

3 算例分析

3.1 滤波器参数与控制策略对节点类型等效的影响分析

对图1所示的单逆变器并网,通过仿真等手段可以证明,当控制器采取鲁棒下垂控制时,由于其P-ω和Q-V环节均带积分器,无论滤波器参数和线路参数Zline的取值如何,稳态时式(8)和式(9)均成立。故可等效为P(ω)-Q(V)节点。

若采取图2所示的下垂控制器,则逆变器实际注入电网的无功功率与滤波器的参数有关。根据附录A表A1和表A2的调研结果,若取Zline=0.028 629+j0.002 798,滤波电感L=2 mH,滤波电容C为40 μF。E*=1.01,n=0.1,Pref=1.0(标幺值),Qref=0(标幺值),无穷大母线电压为1.0(标幺值),频率为50 Hz。附录A表A3给出了当滤波电感L变化20%,-20%,0,10%,-10%这5种情况下系统无功功率和电压的变化情况。从中可见,虽然其有功功率部分满足P-ω关系,但输出无功功率与端电压之间不再是确定的下垂系数为n的关系。对潮流计算而言,该控制器也就难以用现有的节点等效类型去描述。

3.2 基于欧盟微电网的算例分析

本文以欧盟提出的微电网结构[21]为基础,额外补充运行参数,搭建了图4所示的含鲁棒下垂控制、PQ控制逆变器的20节点微电网系统进行分析,说明本文所提潮流算法的有效性。

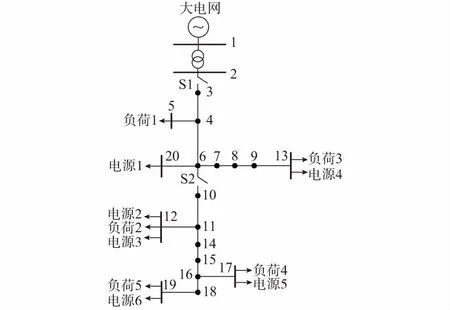
图4 20节点微电网结构Fig.4 Structure of 20-node microgrid

该系统的网络参数见附录A表A4,其中P+jQ为负荷或电源的有功功率和无功功率,其余参数意义同前。微电网孤岛运行时开关S1断开,S2闭合。20号节点设为平衡节点,其电压幅值设为1.05(标幺值),参考相位为0°;5号节点单独接入负载;12,13,17,19号节点同时接入负载与电源。其中电源2和4为恒功率电源;电源1,3,5,6均采用鲁棒下垂控制策略,且下垂系数的选取和电源的功率呈反比。这种措施使得逆变器输出功率可以依照容量进行等比例均分,有利于微电网的自治运行。

利用附录A表A4的输入数据和本文给出的潮流算法进行计算,结果如附录A表A5所示。此时系统的频率为0.996 4(标幺值)。同时,表A5中的电源3,5,6实现了有功功率按容量的精确分配,而无功功率由于受各节点电压的影响,虽未实现精确分配,也可近似分配。各电源未出现功率越限情况。

若需验证功率越限方式的正确性,则可设置附录A表A4中的下垂系数mi和ni统一为0.005和2。潮流计算的结果如附录A表A6所示,系统的频率为0.997 7(标幺值)。电源6的输出有功功率和无功功率均达上限,表明本文所提算法功率越限工况的处理有效。下垂系数的变化也导致电源3,5,6输出有功功率不再按照容量分配。由此可见,下垂系数的选择确实会对微电网频率、潮流分布和逆变器的功率分配等有明显影响。

4 结语

本文提出了评价逆变器控制策略是否适宜潮流计算的问题,总结了逆变器节点的等效条件。针对鲁棒下垂控制器,给出了潮流计算算法,并用欧盟微电网的参数予以验证。主要结论如下。

1)从潮流计算的角度来说,对于逆变器的控制策略,若其调制波幅值、频率和相位产生环节均引入积分器,则可利用稳态时积分器输入为0的特点进行节点类型等效。可归纳为此类控制器的有PQ,Vf,鲁棒下垂控制和部分符合这个特点的VSG控制。

2)由于低压微电网中逆变器滤波器的阻抗显著高于线路的阻抗,经典下垂控制无法等效为传统潮流计算的节点类型。采用P(ω)-Q(V)节点类型进行潮流计算有可能得到严重错误的结果。

3)针对可归为P(ω)-Q(V)类型节点的鲁棒下垂控制器,可采用统一迭代的潮流计算方法。控制器系数选取对系统潮流状态有明显影响。

下垂控制是一类广泛应用的控制策略,本文证明了其不适合用当前节点类型等效的方法进行潮流计算。此类控制器的潮流算法将是下一步研究工作的重点。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参 考 文 献

[1] 周烨,汪可友,李国杰,等.基于多智能体一致性算法的微电网分布式分层控制策略[J].电力系统自动化,2017,41(11):142-149.DOI:10.7500/AEPS20160920004.

ZHOU Ye, WANG Keyou, LI Guojie, et al. Distributed hierarchical control for microgrid based on multi-agent consensus algorithm[J]. Automation of Electric Power Systems, 2017, 41(11): 142-149. DOI: 10.7500/AEPS20160920004.

[2] 陈刚,杨毅,杨晓梅,等.基于分布式牛顿法的微电网群分布式优化调度方法[J].电力系统自动化,2017,41(21):156-162.DOI:10.7500/AEPS20170313007.

CHEN Gang, YANG Yi, YANG Xiaomei, et al. Distributed optimization scheduling method for microgrid cluster based on distributed newton method[J]. Automation of Electric Power Systems, 2017, 41(21): 156-162. DOI: 10.7500/AEPS20170313007.

[3] 曾正,李辉,冉立.交流微电网逆变器控制策略述评[J].电力系统自动化,2016,40(9):142-151.DOI:10.7500/AEPS20150226006.

ZENG Zheng, LI Hui, RAN Li. Comparison on control strategies of inverters in AC microgrids[J]. Automation of Electric Power Systems, 2016, 40(9): 142-151. DOI: 10.7500/AEPS20150226006.

[4] LISERRE M, BLAABJERG F, HANSEN S. Design and control of an LCL-filter based three-phase active rectifier[C]// IEEE Industry Applications Conference, September 30-October 4, 2001, Chicago, USA: 299-307.

[5] 彭咏龙,朱劲波,李亚斌.基于电感电压反馈和输入整形技术的LC滤波器混合阻尼控制[J].电力系统保护与控制,2015,43(2):103-107.

PENG Yonglong, ZHU Jinbo, LI Yabin. Hybrid damping control based on the LC filter inductor voltage feedback and input shaping techniques[J]. Power System Protection and Control, 2015, 43 (2): 103-107.

[6] ZHONG Qingchang. Harmonic droop controller to reduce the voltage harmonics of inverters[J]. IEEE Transactions on Industrial Electronics, 2013, 60(3): 936-945.

[7] PIAGI P, LASSETER R H. Autonomous control of microgrids[C]// IEEE Power Engineering Society General Meeting, June 18-22, 2006, Montreal, Canada: 8p.

[8] ZHONG Qingchang. Robust droop controller for accurate proportional load sharing among inverters operated in parallel[J]. IEEE Transactions on Industrial Electronics, 2013, 60(4): 1281-1290.

[9] ZHONG Qingchang, WEISS G. Static synchronous generators for distributed generation and renewable energy[C]// IEEE/PES Power Systems Conference and Exposition, March 15-18, 2009, Seattle, USA: 6p.

[10] 李培帅,施烨,吴在军,等.孤岛微电网潮流的类奔德斯分解算法[J].电力系统自动化,2017,41(14):119-125.DOI:10.7500/AEPS20160627002.

LI Peishuai, SHI Ye, WU Zaijun, et al. Power flow calculation method similar to Benders decomposition for islanded microgrid[J]. Automation of Electric Power Systems, 2017, 41(14): 119-125. DOI: 10.7500/AEPS20160627002.

[11] ZHU Y, TOMSOVIC K. Adaptive power flow method for distribution systems with dispersed generation[J]. IEEE Power Engineering Review, 2002, 22(5): 72-72.

[12] 陈海焱,陈金富,段献忠.含分布式电源的配电网潮流计算[J].电力系统自动化,2006,30(1):35-40.

CHEN Haiyan, CHEN Jinfu, DUAN Xianzhong. Study on power flow calculation of distribution system with DGs[J]. Automation of Electric Power Systems, 2006, 30(1): 35-40.

[13] 王聪,颜伟,赵霞,等.考虑逆变电源控制模式的微电网三相潮流模型[J].中国电机工程学报,2015,35(12):2960-2967.

WANG Cong, YAN Wei, ZHAO Xia, et al. Three-phase power flow model for microgrid considering inverter control modes[J]. Proceedings of the CSEE, 2015, 35(12): 2960-2967.

[14] 王逸超,罗安,金国彬.微网逆变器的改进鲁棒下垂多环控制[J].电工技术学报,2015,30(22):116-123.

WANG Yichao, LUO An, JIN Guobin. Improved robust droop multiple loop control for parallel inverters in microgrid[J]. Transactions of China Electrotechnical Society, 2015, 30(22): 116-123.

[15] 王成山,李琰,彭克.分布式电源并网逆变器典型控制方法综述[J].电力系统及其自动化学报,2012,24(2):12-20.

WANG Chengshan, LI Yan, PENG Ke. Overview of typical control methods for grid-connected inverters of distributed generation[J]. Proceedings of the CSU-EPSA, 2012, 24(2): 12-20.

[16] 王成山,孙充勃,彭克,等.微电网交直流混合潮流算法研究[J].中国电机工程学报,2013,33(4):8-15.

WANG Chengshan, SUN Chongbo, PENG Ke, et al. Study on AC-DC hybrid power flow algorithm for microgrid[J]. Proceedings of the CSEE, 2013, 33(4): 8-15.

[17] BUSO S, CALDOGNETTO T. Rapid prototyping of digital controllers for microgrid inverters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(2): 440-450.

[18] LEI Q, PENG F Z, YANG S. Multiloop control method for high-performance microgrid inverter through load voltage and current decoupling with only output voltage feedback[J]. IEEE Transactions on Power Electronics, 2011, 26(3): 953-960.

[19] YE Q, MO R, LI H. Multiple resonances mitigation of paralleled inverters in a solid-state transformer (SST) enabled AC microgrid[J]. IEEE Transactions on Smart Grid[2017-05-20]. DOI: 10.1109/TSG.2017.2669261.

[20] RAMEZANI M, LI S, SUN Y. Combining droop and direct current vector control for control of parallel inverters in microgrid[J]. IET Renewable Power Generation, 2017, 11(1): 107-114.

[21] PAPATHANASSIOU S, HATZIARGYRIOU N, STRUNZ K. A benchmark low voltage microgrid network[C]// CIGRE Symposium, April 13-16, 2005, Athens, Greece: 5p.

[22] D’ARCO S, SUUL J A, FOSSO O B. Small-signal modeling and parametric sensitivity of a virtual synchronous machine in islanded operation[J]. International Journal of Electrical Power & Energy Systems, 2015, 72: 3-15.

[23] 孟祥萍,高嬿.电力系统分析[M].北京:高等教育出版社,2004.