适用于CPU+GPU协同架构的大规模病态潮流求解方法

王明轩， 陈 颖， 黄少伟， 魏 巍， 常晓青

(1. 清华大学电机工程与应用电子技术系， 北京市 100084； 2. 国网四川省电力公司电力科学研究院， 四川省成都市 610072)

0 引言

随着电网规模的不断扩大和智能电网的进一步发展，其远距离、重负荷、大区域联网的特点日益凸显[1-2]。对于某些重负荷系统、梳状放射性系统或具有邻近多解的系统，潮流方程常常呈现病态。此时，普通潮流算法无法收敛，需要采用病态潮流算法。

病态潮流算法的相关研究由来已久。文献[3-5]提出并发展了最优乘子法，即在牛顿—拉夫逊法的基础上进行了鲁棒性变换，添加乘子并优选其数值，从而搜索病态潮流解。文献[6]采用隐式Cholesky分解方法进行大规模病态潮流计算。文献[7]则利用状态空间搜索的方法研究了病态系统的求解问题。文献[8]构造了基于同伦法的病态潮流算法，该方法发挥同伦方法的大范围收敛性，使得病态潮流易于收敛。

由于含有特殊处理逻辑，计算效率较低，前述病态潮流算法一般并不适合求解普通潮流。文献[9]则提出了基于连续牛顿法(continuous Newton’s method，CNM)的潮流求解方法，同时适用于普通和病态潮流求解。该方法将潮流方程组等效为常微分方程组，进而可采用不同的数值积分方法求取其稳态，对应获得原始潮流方程的解。上述方法虽然通用性较强，但由于算法复杂度较高，求解大规模(病态)潮流时效率较低。因此，有必要研究相关加速方法，提升大规模电网基于CNM的病态潮流算法在线应用能力。

针对基于CNM的潮流求解方法，本文采用定雅可比矩阵和2阶龙格—库塔(RK)方法实现算法逻辑。进一步，采用中央处理器+图形处理器(CPU+GPU)协同计算架构对大规模潮流计算过程进行加速。设计了GPU计算内核，采用海量并发线程完成潮流求解所涉节点不平衡功率计算；根据计算规模和计算内容的不同特性，优选软硬件组合提升其计算效率。最后，以大规模病态潮流算例证明所提方法的正确性和实用性。

1 基于CNM的潮流计算方法及其改进

电网潮流可用如下非线性方程组描述：

f(x)=0

(1)

CNM将上式转换为以下常微分方程组：

(2)

式中：J(x)为f(x)在x处的雅可比矩阵。

为减少LU分解计算量，对式(2)进行改造，采用初始点处的定雅可比矩阵J0替换J(x)，形成式(3)。

(3)

文献[10-11]对采用J0时算法的收敛性进行了理论论证，同时指出该定常处理可能使得收敛速度变慢。但考虑到LU分解在并行架构下的巨大计算量，采用该处理对于提高本文算法整体计算效率是有意义的。给定合适的初值，对式(3)进行积分，所得稳态平衡点即为原潮流方程的解。相应的，经过比选，本文选择二阶显式龙格—库塔(RK2)方法[12]对式(3)进行积分计算，具体流程如附录A图A1所示。算法中在判定潮流收敛的同时，考虑了待求量改变幅度和积分时的限制，兼顾了效率和准确性。

2 CPU+GPU协同架构下的求解方法

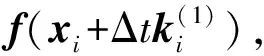
2.1 J0的LU分解

CPU+GPU架构中，稀疏矩阵LU分解可采用Right-looking，Left-looking[13]及Crout分解方法[14]等。本文采用了适用于CPU的NICSLU[15]和PARDISO[16]计算库，以及适用于GPU的cuSOLVER[17]计算库进行稀疏矩阵的LU分解。后文给出了基于不同数学库对典型电网雅可比矩阵进行LU分解的性能对比。通过比选，本文采用NICSLU进行J0的稀疏矩阵LU分解，其特色在于使用Left-looking方法，并可输出J0因子表，方便连续积分计算。

2.2 潮流右端项并行计算

经过前述改进，所提CNM潮流计算中，潮流右端项(向量)计算是重要的一部分。为了提升其计算效率，设计了专门的GPU核函数实现多线程并行处理。

以单节点有功不平衡量计算为例(其余同理)，相关计算可以拆分为以下两个部分，

(4)

考虑到导纳矩阵中大部分元素为0，非零元素为与b条线路对应的2b个非对角元素及N个对角元素。因而，可设计(b+N)个线程，每个线程计算一个非零元素对于与其相关的电流项I产生的递加量，并将电流项与递加量相加。这样实现了排零细粒度并行处理。另一方面，不同线程可能需要同时写入I的某一元素，从而带来了资源访问竞争，阻塞了GPU中的并行计算。为消除此现象，本文采用原子加法操作(atomicAdd函数)实现I并发修正。

如图1所示对上述并发计算过程进行了描述，相关GPU核函数伪代码见附录A表A1。

由以上方法得到向量I之后，根据式(4)中的第1个式子，重新安排n个线程，每个线程进行单个元素的计算，即可得到n维潮流右端项(向量)。

2.3 前代回代求解

前代回代过程实际上是稀疏矩阵为上三角和下三角矩阵的线性方程组的求解过程。同样，在本文潮流算法中需要进行稀疏的前代回代计算，每步积分需要进行两次前代回代。

有多个提供稀疏前代回代算法实现的CPU与GPU数学库，其中适用于CPU的NICSLU库和适用于GPU的cuSPARSE库[15]效率较高，且接口友好。后文给出了基于以上两种数学库完成潮流求解的前代回代部分的性能比较。通过对比，本文采用NICSLU计算库进行前代回代求解。

3 算例测试

3.1 测试平台

进行测试的软、硬件平台如附录B表B1所示。其中正确性测试仅在CPU上完成。

3.2 测试算例

本文采用了不同节点数目的6个算例。将39节点算例称为case39，其余同理。case39和case300均为IEEE标准算例，case2383，case3120，case9241，case13659均取自MATPOWER 6.0，其中case2383和case3120分别来自2000年冬季和2008年夏季的波兰电网数据，case9241和case13659则为来自欧洲电网的真实算例。所采用的最大规模的算例节点数目为13 659，方程组维数为23 225。所计算的均为交流潮流，结果精度为10-4。涉及的时间测试结果均为运行1 000次的平均耗时。

3.3 正确性测试

病态潮流常由于负荷增长引起。负荷增长可能有多种方向，本文测试时采用固定比例同步增长方法。为不失一般性，以case3120为例分析其正确性测试结果，在标准算例的基础上不断增加所有负荷功率和发电机有功出力。负荷因子值增大时采用本文算法求解所需的迭代次数如表1所示。系统未进入病态时迭代次数为10次左右。随着负荷水平提高，系统开始进入病态，算法收敛性变差，迭代次数随着病态程度加重而增加，同时算法求解速度下降。负载和发电机出力达到基态的2.3倍时，传统的牛顿—拉夫逊法已无法收敛。此时采用本文算法，系统残差r=‖f(xi)‖随虚拟时间增长变化如图2所示，残差逐渐趋于0，病态潮流得解。负荷因子进一步增长至2.5时，本文算法也无法收敛。

表1 不同负荷因子时的算法迭代次数Table 1 Iteration times for different load factors

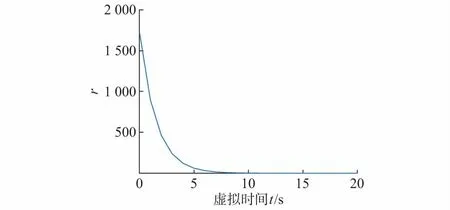
图2 潮流病态求解残差曲线Fig.2 Residual curve of ill-conditioned case

为进一步证明本文方法的正确性，以预测—校正法进行计算时相应病态潮流断面的结果作为参考值，计算本文算法相应的电压和相角误差值。为证明采用定雅可比矩阵的合理性，同时添加采用变雅可比矩阵的测试结果作为对比。针对不同规模的病态潮流算例进行验证，结果如表2所示，表中误差值为各个节点的电压和相角与参考值作差的绝对值中的最大值。电压误差(标幺值)和相角误差(弧度)都不超过0.005，在工程可允许的范围内。

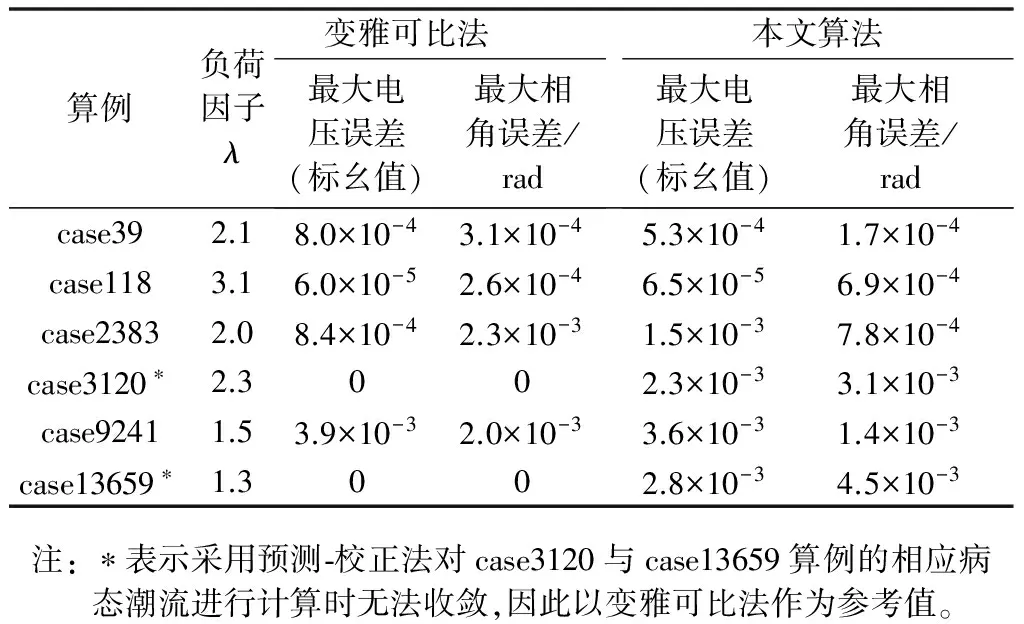
表2 算法正确性测试Table 2 Method accuracy test

3.4 效率测试

3.4.1LU分解计算部分

采用NICSLU，cuSOLVER，PARDISO三种计算库进行电力系统雅可比矩阵分解，计算效率对比如附录B图B1所示。结果显示，NICSLU计算库耗时更短，具有更高的效率。其高效性在矩阵维数较大时更为明显。

3.4.2潮流右端项计算部分

下文比较基于GPU和CPU的潮流右端项计算效率。附录B图B2展示了不同算例基于CNM的潮流计算中该部分计算总耗时的差异。结果表明，在算例规模较小时采用CPU计算潮流右端项效率更高；而在算例规模较大时，GPU算法可取得明显加速效果，其加速比变化趋势如附录B图B3所示。

3.4.3前代回代计算部分

采用NICSLU计算库与cuSPARSE计算库分别完成前代回代求解，比较不同算例基于CNM的潮流求解中该部分计算总耗时，结果如附录B图B4所示。NICSLU库中的前代回代计算在各种规模下均更加高效。

3.4.4整体计算效率

根据前文测试，设计切换规则，针对病态潮流求解所涉计算内容可选择不同实现方法，使得算法执行总体效率最优。具体包括：①对于小于1 000节点的小规模算例，潮流右端项计算在CPU上完成，求解更大规模的算例时，则在GPU上完成潮流右端项计算；②前代回代求解部分均在CPU上完成，其中大于1 000节点的算例求解中涉及CPU与GPU间的通信，但此类通信耗时占比极小，不影响整体算法效率。

根据以上规则，对算法进行整体耗时测试。其中病态潮流算例仍由固定比例同步增长方法得到。值得注意的是，步长Δt的选取对算法收敛性及收敛结果有较大影响，步长过大可能会造成无法收敛的结果。对于本文算法，选取Δt=1.0是对于所有算例可行的一个参数值。为进一步加快迭代收敛的速度，本文根据不同系统的具体情况，对Δt进行了一定的修正，修正原则为尽量选取使得结果正确且迭代次数最少的Δt值。

整体效率测试结果及步长修正情况如表3所示。表中Δt为不同算例整定的步长参数值。可以看出，整体算法具有较高的效率，对于10 000节点以上规模的系统，可以在100 ms左右完成普通潮流和病态潮流求解。

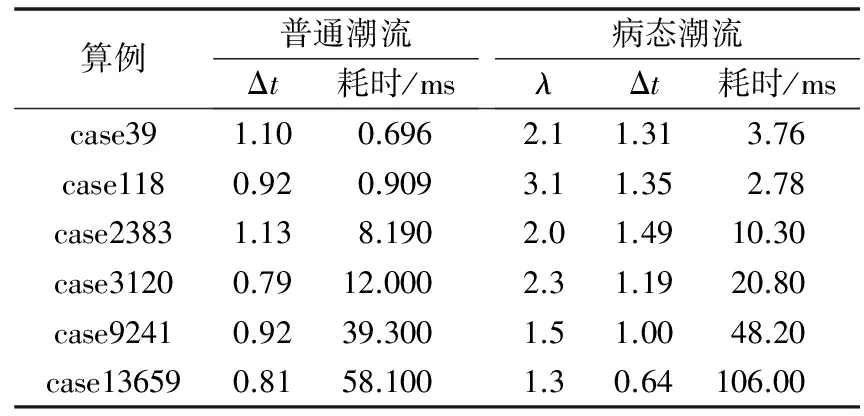
表3 整体计算效率测试Table 3 Efficiency test of all calculations

以case13659的普通潮流计算为例，各部分计算占比如附录B图B5所示。经优化，潮流右端项计算占比已经非常小；而LU分解计算虽仅一次，仍占据了大量时间，这也证明了采用定雅可比矩阵的必要性。减少LU分解次数和耗时对于提高整体算法效率十分重要。

4 结语

本文设计并完成了适用于CPU+GPU协同架构的大规模病态潮流计算方法。将CNM应用于大规模病态潮流求解中并进行相关改进，形成高效大规模病态潮流计算方法，并验证了所提方法的正确性和高效性。本文研究仅针对病态负荷水平下潮流的单次计算过程，没有解决在负荷增加过程中的潮流连续求解问题。在本文算法基础上，后续工作将开展大规模连续潮流GPU加速并行计算的相关研究。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参 考 文 献

[1] 李立浧,张勇军,陈泽兴,等.智能电网与能源网融合的模式及其发展前景[J].电力系统自动化,2016,40(11):1-9.DOI:10.7500/AEPS20150912002.

LI Licheng, ZHANG Yongjun, CHEN Zexing, et al. Merger between smart grid and energy-net: mode and development prospects[J]. Automation of Electric Power Systems, 2016, 40(11): 1-9. DOI: 10.7500/AEPS20150912002.

[2] 于宏文,郑春伟,汪洋,等.智能电网调度控制系统中历史数据服务优化方案[J].电力系统自动化,2016,40(19):113-118.DOI:10.7500/AEPS20150928001.

YU Hongwen, ZHENG Chunwei, WANG Yang, et al. Historical data service optimization scheme for smart grid dispatching and control systems[J]. Automation of Electric Power Systems, 2016, 40(19): 113-118. DOI: 10.7500/AEPS20150928001.

[3] IWAMOTO S, TAMURA Y. A load flow calculation method for ill-conditioned power systems[J]. IEEE Transactions on Power Apparatus and Systems, 1981, 100(4): 1736-1743.

[4] 杜正春,周佃民,董继民.考虑负荷电压静特性的最佳乘子牛顿潮流算法[J].中国电机工程学报,2002,22(1):102-105.

DU Zhengchun, ZHOU Dianmin, DONG Jimin. Optimal multiplier Newton method of load flow with static load characteristics[J]. Proceedings of the CSEE, 2002, 22(1): 102-105.

[5] 胡泽春,王锡凡.基于最优乘子潮流确定静态电压稳定临界点[J].电力系统自动化,2006,30(6):6-11.

HU Zechun, WANG Xifan. Determination of static voltage collapse critical point based on load flow method with optimal multiplier[J]. Automation of Electric Power Systems, 2006, 30(6): 6-11.

[6] 张道天,严正,徐潇源,等.采用隐式Cholesky分解的大规模病态潮流计算[J].电网技术,2016,40(4):1197-1203.

ZHANG Daotian, YAN Zheng, XU Xiaoyuan, et al. Large-scale ill-conditioned power flow calculation using implicit Cholesky factorization method[J]. Power System Technology, 2016, 40(4): 1197-1203.

[7] SHAHRIARI A, MOKHLIS H, BAKAR A H A, et al. The calculation of low voltage solution based on state space search method in ill-conditioned system[J]. Corrosion Science, 2012, 20(8/9): 1059-1066.

[8] 周佃民,廖培金.电力系统病态潮流的同伦方法求解[J].电力系统及其自动化学报,1999,11(5/6):67-71.

ZHOU Dianmin, LIAO Peijin. Homotopy method for ill-conditioned power system load flow calculation[J]. Proceedings of the CSU-EPSA, 1999, 11(5/6): 67-71.

[9] MILANO F. Continuous Newton’s method for power flow analysis[J]. IEEE Transactions on Power Systems, 2009, 24(1): 50-57.

[10] RAMM A G, SMIRNOVA A B, FAVINI A. Continuous modified Newton’s-type method for nonlinear operator equations[J]. Annali Di Matematica Pura Ed Applicata, 2003, 182(1): 37-52.

[11] AIRAPETYAN R. Continuous Newton method and its modification[J]. Applicable Analysis, 1999, 73(3/4): 463-484.

[12] BUTCHER J C. The numerical analysis of ordinary differential equations: Runge-Kutta and general linear methods[J]. Mathematics of Computation, 1987, 51(183): 693.

[13] SCHENK O, GRTNER K, FICHTNER W. Efficient sparse LU factorization with left-right looking strategy on shared memory multiprocessors[J]. Bit Numerical Mathematics, 2000, 40(1): 158-176.

[14] FORD W. Chapter 11—Gaussian elimination and the LU decomposition[M]// Numerical Linear Algebra with Applications, 2015: 205-239.

[15] CHEN X, WANG Y, YANG H. NICSLU: an adaptive sparse matrix solver for parallel circuit simulation[M]. Piscataway, USA: IEEE Press, 2013.

[16] SCHENK O, GRTNER K. PARDISO[M]. Boston: Springer, 2011: 1458-1464.

[17] NVIDIA. CUDA toolkit documentation v8.0[EB/OL]. [2017-06-23]. http://docs.nvidia.com/cuda/index.html.