分布式协同控制模式下配电网信息物理系统脆弱性评估

李培恺, 刘 云, 辛焕海, 齐冬莲

(1. 浙江大学电气工程学院, 浙江省杭州市 310027; 2. 深圳大学机电与控制工程学院, 广东省深圳市 518060)

0 引言

当前,低碳经济、能源多样化和可持续发展成为了电力系统关注的焦点[1]。在此背景下,可再生新能源分布式发电技术凭借其清洁、效率高等优点逐渐广泛地应用于电力系统中,成为了传统集中式发电形式的有效补充[2]。分布式电源(distributed generator,DG)通常接入于配电网侧,并可通过减小电能传输损耗、改善电能质量和满足本地负荷需求等方式提升系统的性能[3]。

然而,当DG逐渐大规模地接入电网后,考虑到其单机容量小、出力波动性大以及地理位置分布广泛的特点,电力调度中心难以继续按照传统集中式控制模式对它们逐一进行管理。为此,分布式协同控制仅通过信息局部传递即可完成全局调度目标,具有经济性好、通信鲁棒性强以及能够满足分布式终端即插即用特性等优点,为这一问题的解决提供了有效途径。基于上述优越性,分布式协同控制方法于近年来得到了逐渐广泛的关注和研究。具体地,在满足系统总有功出力调度目标的前提下,文献[4-5]提出的协同控制方法通过协调各光伏机组的实际出力使之与各自的最大允许出力的比值相等,以实现出力的公平分配;文献[6-8]则针对经济调度问题,研究一种基于新能源发电机组等成本微增率的协同控制算法,以使出力经济性达到最优。

为实现分布式协同控制模式在电网中的应用,需构建电力信息物理系统(cyber-physical system,CPS),从而加强系统对物理设备的即时感控能力,并促使网络信息的双向流动和高效利用。电力CPS融合了信息技术、通信技术和控制技术[9],适应于现代电网对信息共享和协作能力的需求,正成为当今电力系统建设发展的目标。但同时,其信息物理紧密融合的特点,也方便了网络攻击者通过电力信息层威胁物理系统的安全稳定运行,即为电网引入了诸多威胁因素[10]。因此,研究建立电力CPS在网络攻防环境下的系统脆弱性评估体系就具有了理论价值和实际意义。

然而,目前国内外所采用的电力系统脆弱性评估方法普遍是以复杂网络理论[11-13]、暂态能量函数[14-15]、概率统计[16-17]等数学理论为基础,直接分析电力一次侧物理设备或二次侧信息节点被破坏后系统抗干扰及持续运行的能力,少有结合CPS信息物理融合特点及网络攻击者动态行为开展的研究工作。在现阶段的有关研究中,文献[18-20]在复杂网络理论的基础上进行延伸,建立了电力信息—物理相互依存模型,以表征信息物理耦合影响机理,在此基础上研究探讨网络攻击威胁下电力CPS的脆弱性影响因素。文献[21-23]运用攻击图理论,依据通信网络拓扑、信息元件状态以及攻击者入侵算法等构建网络攻击者潜在攻击路径概率模型,并对电力CPS中的脆弱节点进行综合评价量化得到脆弱性评估指标,以定量评估系统遭受网络攻击时的脆弱性。为规避上述方法无法充分计及攻防双方动态决策的缺陷,文献[24-26]从博弈论角度出发,建立攻防模型以表征攻击者和防御者策略,设计博弈函数以模拟实际攻防互作用场景,最终根据博弈过程造成的电网损失情况评估电力CPS的脆弱性。但上述基于博弈论的研究工作仍存在一定的局限性:①对电力CPS脆弱性的分析仍处于起步阶段,仅从宏观层面对网络攻防博弈过程进行了梳理,并未结合实际中电网控制调度模式及控制算法动态展开研究;②仅直接考虑网络攻击对电力CPS物理层的影响,未能结合通信网络拓扑进行综合考量;③攻防博弈模型侧重于以电网防御者视角进行构建,缺少对于攻击成功率及攻击成本效益等网络攻击方约束条件的考虑。

为破除现阶段工作的局限性并实现对于网络攻击威胁下采用分布式协同控制模式的配电网CPS脆弱性的量化评估,本文提出了一种基于动态攻防博弈的评估方法。该方法首先基于CPS风险评估框架,结合DG协同控制策略及实际网络攻防策略的特点,建立含协同控制的配电网CPS风险评估模型;在此基础上,进行动态攻防博弈以对系统风险进行评估,从而得到分布式协同控制模式下配电网CPS脆弱性的量化结果;最后,基于仿真测试系统对该量化评估方法的有效性进行了验证。

1 DG协同控制策略

1.1 图论基础

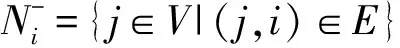
(1)

式中:aij为A中第i行第j列元素。

1.2 DG的等输出比协同控制策略

在配电网CPS中,可通过虚拟发电厂(virtual power plant,VPP)技术将众多小型分布式发电单元聚合为一个可控整体参与到电网运行中[27],实现对配电网侧高密度异构DG的统筹管理,其结构如图1所示(Ci为通信节点)。其中,信息层同时包含虚拟发电厂内部通信及其与配电网之间的通信联系。

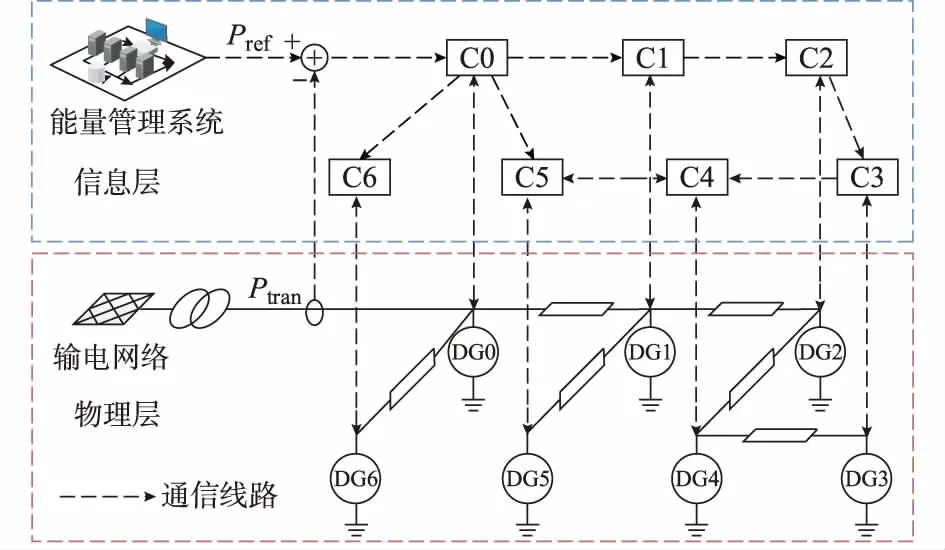
图1 虚拟发电厂协同控制结构图Fig.1 Structure diagram of cooperative control for VPP

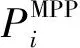
(2)

式中:α*为一致性输出比;Ptran为各DG输出功率P=[P0,P1,…,Pn]T的函数(当配电网向输电网输出功率时Ptran为正,否则为负),并可通过在配电网总馈线处直接采集[4]或分布式地搜集各DG实际出力及负荷信息[5]来获取Ptran的实时数值。

为分布式地实现上述控制目标,各DG的输出比αi(k)采用离散时间的领导—跟随一致性算法进行计算,其中领导DG具有获取Ptran(k)信息以及调度指令Pref(k)的权限。不失一般性,选取DG0作为领导DG,其输出比可按照如下原则进行更新:

α0(k+1)=min(max(α0(k)+

ε(Pref-Ptran(k)),0),1)

(3)

式中:ε>0为算法的收敛系数。

在每个迭代周期内,领导DG根据反馈信息Pref-Ptran(k)来调节自身输出比,进而调整虚拟发电厂的总体出力。式(3)将输出比α0(k)控制在区间[0,1]内,即可保证其能够被DG0所实现。

对于跟随DG,其输出比信息根据其接收邻居的状态加权进行更新,即

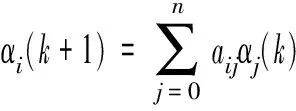
(4)

令α(k)=[α0(k),α1(k),…,αn(k)]T,在满足输出比约束α0(k)∈[0,1]的条件下,可将迭代更新规则(式(3)和式(4))写成统一的矩阵形式:

α(k+1)=Aα(k)+εB(Pref-Ptran(k))

(5)

式中:B=[1,0,…,0]T∈R(n+1)×1。

一般性地,通信网络权重矩阵将根据系统管理者的需求来进行设计。常见的选取方法可参考文献[28],其不同的选取方式将对分布式协同控制算法的收敛进程产生影响。

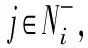
等输出比协同控制的收敛特性可以总结为定理1[29]。

定理1:在满足假设1的条件下,当采用式(5)所示的离散协同控制律时,虚拟发电厂中各DG能够渐近一致地收敛到式(2)的最优解。

2 基于分布式协同控制策略的配电网CPS风险评估模型

DG的协同控制包含频繁的信息传递以及分布式计算过程,因此易于遭受网络攻击的威胁。若电网防御者不事先采取有效的防御措施,则当协同控制系统受到攻击时可能会导致控制目标无法实现。

本节充分考虑网络攻击影响因素,通过在CPS风险评估框架的基础上对网络攻防策略的分析建模,构建出完整的配电网CPS风险评估模型。

2.1 CPS风险评估框架

在遭受网络攻击威胁的环境下,CPS风险评估方法为:

R=PAPDL

(6)

式中:PA为网络攻击成功入侵的概率;PD为若元件遭受攻击,其最终失效的概率;L为元件失效后带来的实际损失大小;R为系统最终损失的期望值,即风险。

式(6)所示的评估方法同时计及了信息层中网络攻击者和主动防御者双方行为对CPS风险水平的影响,并以物理层中的实际损失量作为评判网络攻击对系统危害程度的标准,符合CPS及其攻防环境的特点。在设定适当的网络攻击形式下,该框架可用于对CPS的脆弱性进行评估。

2.2 网络攻防策略模型

实际中,网络攻防双方通常具有各自的攻击/防御资源(包括网络攻击/电网防御行为所需耗费的人力、技术、物理设备以及资金等)。网络攻防双方在各元件上所分配的攻击/防御资源数量的不同,将会影响各元件自身的脆弱性,进而影响整个系统的风险水平。因此,对于一个具有ns个受威胁元件(如DG、通信线路、保护装置和变压器等)的配电网CPS,网络攻击者/电网防御者需决定如何在这些元件之间分配有限的攻击/防御资源,以达到其特定的攻击/防御目的。由此,便构成了网络攻防双方的决策。

2.2.1网络攻击者策略模型

设网络攻击者的攻击策略集合为CA,集合中的每个元素cAi∈CA(i=1,2,…,nA;nA为攻击资源分配方式总数)均代表一种攻击资源的分配方式,即

(7)

(8)

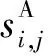
对于网络攻击者而言,其在某一元件上投入的攻击资源越多,则该元件被入侵的概率就越大,二者之间的关系可建模为[26]:

(9)

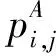
通过式(9),攻击资源在系统元件间的分配情况即可等价为网络攻击入侵成功概率的分布。

2.2.2电网防御者策略模型

与网络攻击者策略类似,电网防御者也需要决定如何分配其有限的数量为SD的防御资源到系统ns个受威胁元件之中。设电网防御者的防御策略集合为CD,集合中的每个元素cDi∈CD,(i=1,2,…,nD;nD为防御资源分配方式总数)均代表一种防御资源的分配方式。那么同样地,电网防御者的策略可以建模为:

(10)

(11)

(12)

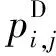
2.2.3调度功率稳定缺额

在配电网CPS中,元件失效后可能带来的损失包括设备停运经济损失、失负荷量、停电时间以及设备维修费用等。本文假设网络攻击者只选取DG信息节点为攻击目标,且忽略自然资源影响因素。考虑到分布式协同控制方式的特点及控制目标,现提出调度功率稳定缺额ΔPstab作为衡量系统损失L的指标,下面进行说明。

为保障系统安全,当信息层中某一信息节点遭受网络攻击时,其通信邻居均须断开与之相连的通信线路以阻止恶意信息的进一步扩散。据此,则有定义1。

定义1(调度功率稳定缺额):当协同控制系统遭受网络攻击时,受攻击节点被隔离;在此新的通信拓扑下,所有节点仍按照控制策略(式(5))更新出力。当DG出力均稳定后,此时调度指令Pref与实际注入功率Ptran之差即定义为调度功率稳定缺额ΔPstab。

根据该定义,在虚拟发电厂中各DG容量及通信拓扑确定的情况下,ΔPstab的取值只与网络攻击策略、控制调度命令Pref以及网络攻击时刻tA有关。

需要注意的是,在实际中,采取使用本地观测器进行实时监控等高安全等级的专门措施可以保障领导节点不受攻击,然而在经济上却不具备提高每个分布式受控对象安全等级的可行性,因此本文可只讨论跟随节点遭受攻击的情形。同时,依据更新原则式(4),在新的通信拓扑下,只有领导节点及与之仍保持连通的跟随节点可继续接受调度;其余未受攻击的孤岛节点(群)则维持其局部出力。

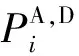
(13)

据此,风险评估框架式(6)可进一步表述为:

(14)

式中:LTj为失效元件组合Tj带来的实际损失量;Nj为Tj所有可能组合的总数。

3 配电网CPS动态攻防博弈模型

3.1 斯塔克尔伯格攻防博弈模型

基于第2节中所建立的策略模型,网络攻防双方在协同控制系统上可构成博弈,即二者均试图通过调整各自的资源分配策略以追求其最大化的效益。对于该攻防博弈,需要在约束条件(式(5)至式(13))下通过求解下述优化问题得到权衡结果:

(15)

对于一个给定的协同控制系统,风险R是一个关于攻防资源总量SA和SD、控制调度命令Pref以及网络攻击时刻tA的函数。在斯塔克尔伯格博弈模式下,该优化问题可通过如下攻防步骤进行求解。

步骤1:在对网络攻击策略未知但有预防的情况下,电网防御者首先制定资源分配策略,将防御资源分配到若干元件上以降低系统被攻击后失效的概率,如式(10)至式(12)所示。

步骤2:在虚拟发电厂根据分布式协同控制调度命令进行出力调整时,网络攻击者根据电网防御者所采取的防御资源分配策略制定攻击策略,在若干对象上分配适量攻击资源以提升成功入侵系统的概率,如式(7)至式(9)所示。

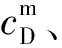
(16)

(17)

(18)

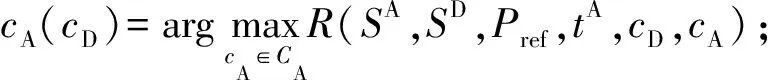
3.2 防御资源分配策略

由3.1节可知,在进行动态攻防博弈求解时,首先需要电网防御者制定防御资源的分配策略。为实现在对网络攻击策略不知情但有预防的情况下能够将有限的防御资源更有效地分配到系统受威胁元件中,本文提出了如下的分配策略。

步骤1:初始时,所有元件上的防御资源均为0;并根据精度要求,将总量为SD的防御资源分成为X份子防御资源。同时,设定电网防御者理想可接受阈值U,并令i=1。

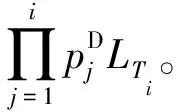
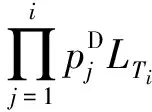
(19)

若无符合条件的元件组合,则直接进入步骤4。

上述防御资源分配策略是基于文献[24]中的分配方法提出的,并考虑了多受攻击对象以及电网可容忍损失程度,使得分配结果更贴合配电网CPS攻防环境的实际。

4 仿真研究及结果分析

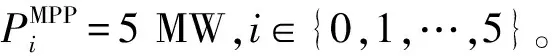
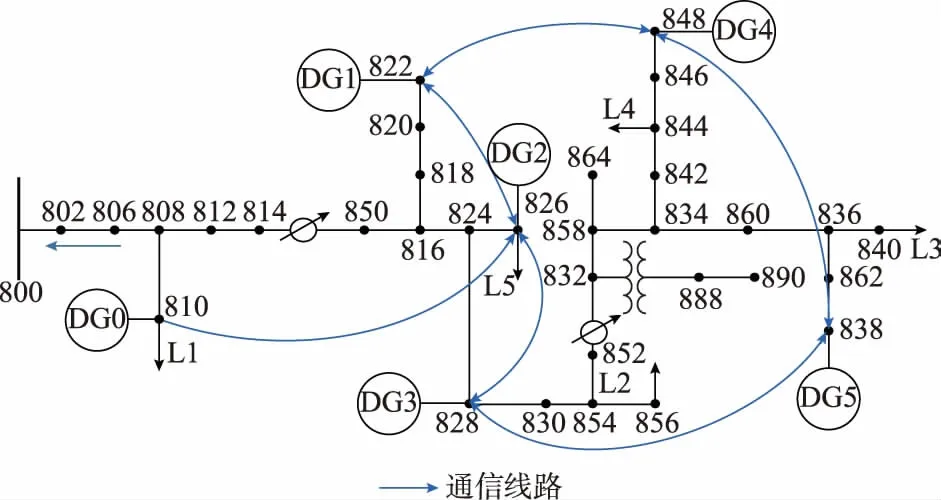
图2 IEEE 34节点配电系统图Fig.2 Diagram of IEEE 34-bus distribution network

4.1 攻防博弈及脆弱性评估结果分析

初始时,上级能量管理系统下发的控制调度命令Pref=16 MW;按照本文的等输出比协同控制策略,此时对于虚拟发电厂中的DGi(∀i∈{0,1,…,5})均有Pi=3 MW,αi=0.6。网络攻击者攻击资源总量SA=10;电网防御者防御资源总量SD=10,防御资源分配精度X=100;电网防御者理想可接受阈值U=0.5 MW。

首先,电网防御者按照本文3.2节中的防御资源分配策略将防御资源分配到各个跟随DG上,最终的分配结果如表1所示。

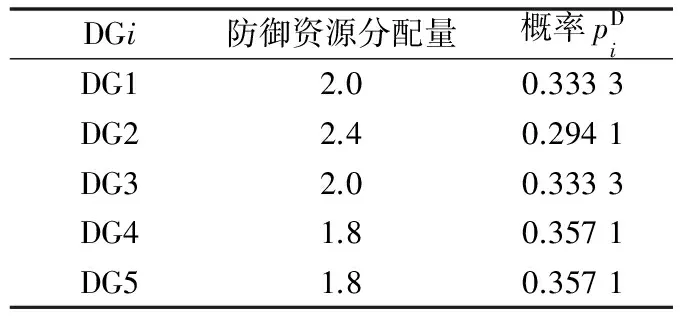
表1 防御资源分配结果Table 1 Result of defense resource allocation

可以看出,DG2被分配到了最多的防御资源。这是由于在虚拟发电厂通信网络中DG2的度数最大,且是与领导DG有直接通信联系的唯一跟随DG,当其被攻击导致失效后会造成最严重的后果,因此理应得到更多保护。

接着,根据上述防御策略,网络攻击者在虚拟发电厂出力稳定的某一时刻发动攻击,将攻击资源适当地分配到若干DG上。网络攻击者考虑可能采用的攻击资源分配策略及造成的风险结果如表2所示(由于数量过多,这里只展示部分结果)。

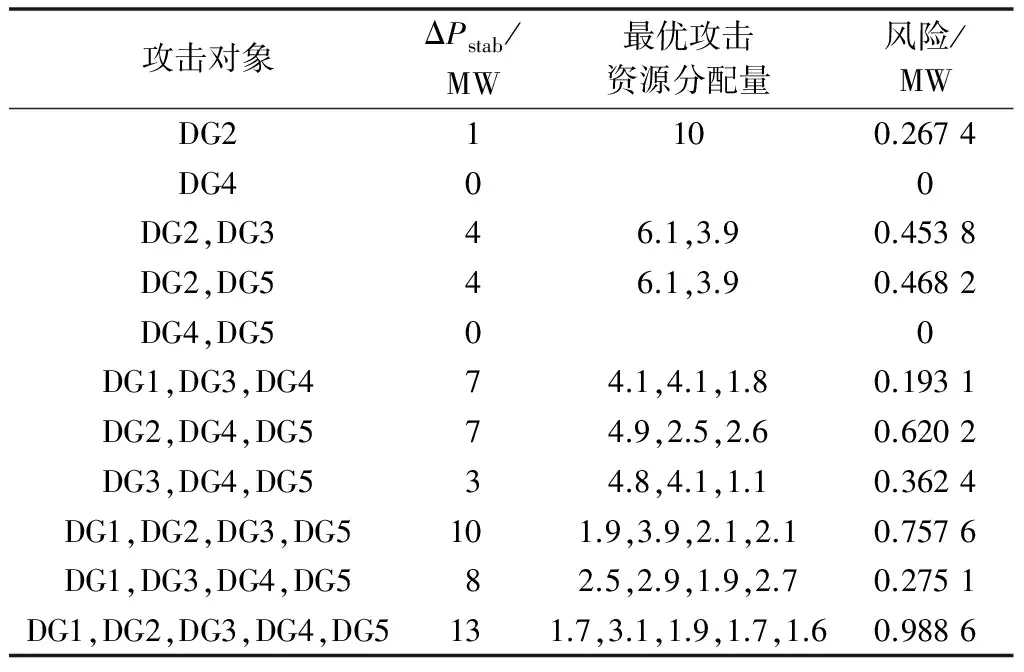
表2 攻击资源分配及风险评估结果Table 2 Results of attack resource allocation and risk assessment

由表2可知,在攻击策略中,即便网络攻击者的攻击对象数量及攻击资源分配方式相同,防御资源分配量及造成的ΔPstab不同仍会导致系统风险存在差异;且尽管当网络攻击者选取越多的攻击对象时造成的ΔPstab也会增大,但由于在选取的攻击对象上分配到的防御资源总量也随之增加,因此最终造成的系统风险未必随之增大。根据遍历计算结果,在已知电网防御者资源分配方案的情况下,网络攻击者采取cA={1.7,3.1,1.9,1.7,1.6}的攻击策略可获得最大化的效益,即当电网防御者采用如表1所示的防御策略后,无论网络攻击者如何分配其攻击资源,系统风险均不会超过0.988 6 MW。

在上述以追求最大效益为目的的蓄意网络攻击下,造成的系统风险R=0.988 6 MW即为该含DG协同控制系统的脆弱性评估结果。

4.2 分布式协同控制系统脆弱性灵敏度分析

在动态攻防博弈过程中,协同控制系统的脆弱性评估结果会受到诸多因素变化的影响,下面将对这些影响因素开展仿真分析。

4.2.1攻防资源总量变化影响因素分析

攻防资源总量SA和SD是在博弈阶段影响系统脆弱性水平的两个关键因素,需对二者进行灵敏度分析。仿真的初始条件与4.1节相同,仿真结果如图3所示。该图展示了随着攻防资源总量的分别变化,在每一资源数量组合(SA,SD)下进行攻防博弈时所对应的系统脆弱性。从图中可以看出,系统脆弱性随着SD的增加而减小,但减小的速度逐渐放缓;另一方面,尽管增加SA确实能增大系统脆弱性,但当SD的数量达到一定程度后,即便SA的大量增加也只能给网络攻击者带来极小的效益增量。这说明,相较于攻击资源总量,防御资源总量的变化更容易对协同控制系统的脆弱性产生影响。

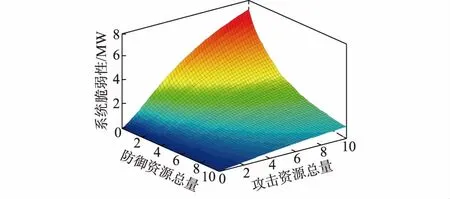
图3 攻防资源总量变化对系统脆弱性影响三维图Fig.3 Three-dimensional diagram of effect of resource amount variation of attacker and defender on vulnerability sensitivity

本小节的仿真结果及分析结论有助于指导采用分布式协同控制模式的配电网CPS防御者,如何根据其所在的CPS攻防环境选取投入适量的防御资源。

4.2.2分布式协同控制动态过程影响因素分析

在博弈阶段中,除了网络攻防双方影响因素,分布式协同控制本身的动态收敛过程也会对系统脆弱性评估结果造成影响。下面先通过仿真算例对影响机理进行说明,再进行灵敏度分析。

设在4.1节的初始条件下,虚拟发电厂按照控制调度命令Pref=21 MW调整出力。该情况下的协同控制动态过程如图4所示。可以注意到,各DG大约在80 s时完成输出比的一致性收敛,虚拟发电厂也同时完成了功率追踪。因此,凡若网络攻击发生在协同控制动态收敛过程的任一时刻,均有可能产生调度功率稳定缺额;在系统结构及攻防策略不变的前提下,该功率缺额的大小将主要取决于网络攻击时刻和控制调度命令变化量。

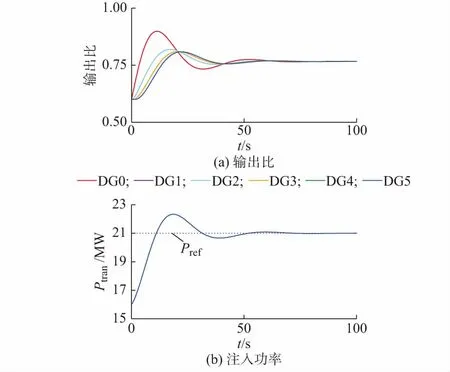
图4 协同控制动态收敛过程Fig.4 Dynamic convergence of cooperative control

不失一般性地,现基于4.1节的初始条件,仿真分析网络攻击时刻和控制调度命令对分布式协同控制脆弱性的影响。仿真结果如图5所示(调度比例指Pref与虚拟发电厂最大允许出力之比),展示了随着虚拟发电厂按照每一控制调度指令进行动态调整,在每一时刻下进行攻防博弈时所对应的系统脆弱性。由图5可知,在虚拟发电厂接受某一Pref调度的过程中,系统脆弱性在开始阶段变化明显,一段时间后则逐渐趋于定值;同时,随着Pref的增大,系统脆弱性也会逐渐提升。这是由于在新的调度命令下,初始时各DG会快速调整自身出力(如图4(a)所示),且ΔPstab与该调度命令取值正相关的缘故。据此,电网防御者可根据虚拟发电厂调度情况提前设防,并根据系统的脆弱性可容忍度合理规划防御资源的投入时机。

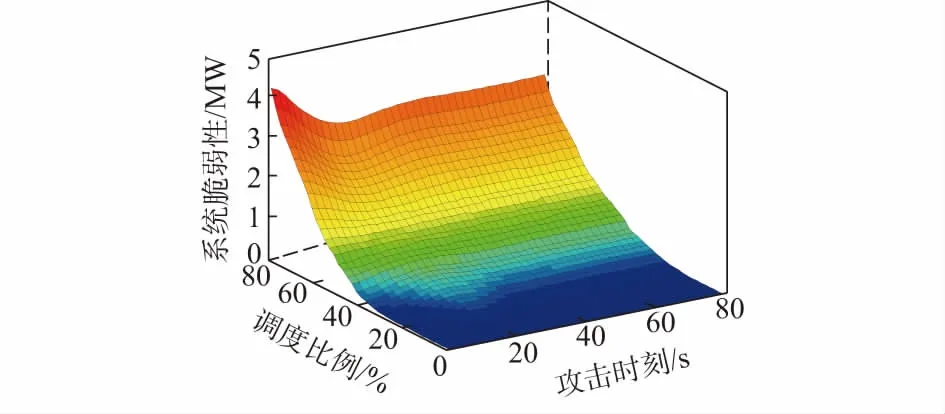
图5 协同控制动态过程对系统脆弱性影响三维图Fig.5 Three-dimensional diagram of effect of dynamic process of cooperative control on vulnerability sensitivity

5 结语

分布式协同控制作为一种未来含高渗透率异构DG配电网CPS的参考管理模式,其安全问题不容忽视。本文运用动态博弈方法对含DG协同控制策略的配电网CPS脆弱性进行量化评估,以从风险角度指导未来协同控制系统的设计。其中,首次结合电力系统实际控制调度方式构建了适用于配电网CPS的风险评估模型;考虑分布式协同控制的特点及其控制目标,提出了调度功率稳定缺额指标以衡量网络攻击对配电网CPS的危害程度;同时计及攻防双方包括可利用资源数量、资源理性分配方式、成本效益、受攻击节点数量等在内的约束条件,建立了更完善的网络攻防策略模型。随着研究的不断深入,CPS的信息物理融合机理必将逐步得到揭示。结合这些新的耦合因素进一步设计CPS脆弱性评估模型,以及由此从更多角度指导协同控制系统的构建将是下一步的研究重点。

本文受到浙江省电力公司科技项目(5211JY15001Q)和深圳大学新引进教师科研启动项目(2018033)资助,特此感谢!

参 考 文 献

[1] 康重庆,陈启鑫,夏清.低碳电力技术的研究展望[J].电网技术,2009,33(2):1-7.

KANG Chongqing, CHEN Qixin, XIA Qing. Prospects of low-carbon electricity[J]. Power System Technology, 2009, 33(2): 1-7.

[2] 王成山,李鹏.分布式发电、微网与智能配电网的发展与挑战[J].电力系统自动化,2010,34(2):10-14.

WANG Chengshan, LI Peng. Development and challenges of distributed generation, the micro-grid and smart distribution system[J]. Automation of Electric Power Systems, 2010, 34(2): 10-14.

[3] 王成山,王守相.分布式发电供能系统若干问题研究[J].电力系统自动化,2008,32(20):1-4.

WANG Chengshan, WANG Shouxiang. Study on some key problems related to distributed generation systems[J]. Automation of Electric Power Systems, 2008, 32(20): 1-4.

[4] XIN H, QU Z, SEUSS J, et al. A self-organizing strategy for power flow control of photovoltaic generators in a distribution network[J]. IEEE Transactions on Power Systems, 2011, 26(3): 1462-1473.

[5] XIN H, LU Z, LIU Y, et al. A center-free control strategy for the coordination of multiple photovoltaic generators[J]. IEEE Transactions on Smart Grid, 2014, 5(3): 1262-1269.

[6] 赵亦岚,陈彬,范元亮,等.虚拟发电厂分布式控制收敛速度分析及优化[J].电网技术,2016,40(8):2288-2295.

ZHAO Yilan, CHEN Bin, FAN Yuanliang, et al. Convergence speed analysis and optimization for distributed control of virtual power plant[J]. Power System Technology, 2016, 40(8): 2288-2295.

[7] YANG Z, XIANG J, LI Y. Distributed consensus based supply-demand balance algorithm for economic dispatch problem in a smart grid with switching graph[J]. IEEE Transactions on Industrial Electronics, 2017, 64(2): 1600-1610.

[8] YANG S, TAN S, XU J X. Consensus based approach for economic dispatch problem in a smart grid[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4416-4426.

[9] 赵俊华,文福拴,薛禹胜,等.电力信息物理融合系统的建模分析与控制研究框架[J].电力系统自动化,2011,35(16):1-8.

ZHAO Junhua, WEN Fushuan, XUE Yusheng, et al. Modeling analysis and control research framework of cyber physical power systems[J]. Automation of Electric Power Systems, 2011, 35(16): 1-8.

[10] 郭嘉,何宇斌,韩宇奇,等.考虑有效距离接近中心性的信息设备重要度评估[J].电力系统自动化,2016,40(23):42-48.DOI:10.7500/AEPS20160515021.

GUO Jia, HE Yubin, HAN Yuqi, et al. Importance assessment of cyber devices considering effective distance based closeness centrality[J]. Automation of Electric Power Systems, 2016, 40(23): 42-48. DOI: 10.7500/AEPS20160515021.

[11] CHOWDHURY T, CHAKRABARTI A, CHANDA C K. Analysis of vulnerability indices of power grid integrated DG units based on complex network theory[C]// Proceedings of 2015 Annual IEEE India Conference, December 17-20, 2015, New Delhi, India: 1-5.

[12] 刘涤尘,冀星沛,王波,等.基于复杂网络理论的电力通信网拓扑脆弱性分析及对策[J].电网技术,2015,39(12):3615-3621.

LIU Dichen, JI Xingpei, WANG Bo, et al. Topological vulnerability analysis and countermeasures of electrical communication[J]. Power System Technology, 2015, 39(12): 3615-3621.

[13] 魏震波,刘俊勇,朱国俊,等.基于电网状态与结构的综合脆弱评估模型[J].电力系统自动化,2009,33(8):11-14.

WEI Zhenbo, LIU Junyong, ZHU Guojun, et al. A new integrative vulnerability evaluation model to power grid based on running state and structure[J]. Automation of Electric Power Systems, 2009, 33(8): 11-14.

[14] 徐行,李华强,赵祥云,等.基于运行状态和网络结构的节点综合脆弱性评估[J].电网技术,2014,38(3):731-735.

XU Xing, LI Huaqiang, ZHAO Xiangyun, et al. Assessment on modal comprehensive vulnerability based on operational state and network structure[J]. Power System Technology, 2014, 38(3): 731-735.

[15] DEMARCO C L, OVERBYE T J. An energy based security measure for assessing vulnerability to voltage collapse[J]. IEEE Transactions on Power Systems, 1990, 5(2): 419-427.

[16] 陈为化,江全元,曹一家,等.基于风险理论的复杂电力系统脆弱性评估[J].电网技术,2005,29(4):12-17.

CHEN Weihua, JIANG Quanyuan, CAO Yijia, et al. Risk-based vulnerability assessment in complex power systems[J]. Power System Technology, 2005, 29(4): 12-17.

[17] MING N, MCCALLEY J D, VITTAL V, et al. Online risk-based security assessment[J]. IEEE Transactions on Power Systems, 2003, 18(1): 258-265.

[18] CHATTOPADHYAY S, DAI H. Estimation of robustness of interdependent networks against failure of nodes[C]// Proceedings of 2016 IEEE Global Communications Conference, December 4-8, 2016, Washington DC, USA: 1-6.

[19] 冀星沛,王波,董朝阳,等.电力信息-物理相互依存网络脆弱性评估及加边保护策略[J].电网技术,2016,40(6):1867-1873.

JI Xingpei, WANG Bo, DONG Zhaoyang, et al. Vulnerability evaluation and link addition protection strategy research of electrical cyber-physical interdependent networks[J]. Power System Technology, 2016, 40(6): 1867-1873.

[20] NGUYEN D T, SHEN Y, THAI M T. Detecting critical nodes in interdependent power networks for vulnerability assessment[J]. IEEE Transactions on Smart Grid, 2013, 4(1): 151-159.

[21] LIU N, ZHANG J, ZHANG H, et al. Security assessment for communication networks of power control systems using attack graph and MCDM[J]. IEEE Transactions on Power Delivery, 2010, 25(3): 1492-1500.

[22] 王宇飞,高昆仑,赵婷,等.基于改进攻击图的电力信息物理系统跨空间连锁故障危害评估[J].中国电机工程学报,2016,36(6):1490-1499.

WANG Yufei, GAO Kunlun, ZHAO Ting, et al. Assessing the harmfulness of cascading failures across space in electric cyber-physical system based on improved attack graph[J]. Proceedings of the CSEE, 2016, 36(6): 1490-1499.

[23] YAN J, GOVINDARASU M, LIU C C, et al. A PMU-based risk assessment framework for power control systems[C]// Proceedings of 2013 IEEE Power & Energy Society General Meeting, July 21-25, 2013, Vancouver, Canada: 1-5.

[24] 石立宝,简洲.基于动态攻防博弈的电力信息物理融合系统脆弱性评估[J].电力系统自动化,2016,40(17):99-105.DOI:10.7500/AEPS20160510002.

SHI Libao, JIAN Zhou. Vulnerability assessment of cyber physical power system based on dynamic attack-defense game model[J]. Automation of Electric Power Systems, 2016, 40(17): 99-105. DOI: 10.7500/AEPS20160510002.

[25] CHEN G, DONG Z Y, HILL D J, et al. Exploring reliable strategies for defending power systems against targeted attacks[J]. IEEE Transactions on Power Systems, 2011, 26(3): 1000-1009.

[26] WEI L, MOGHADASI A H, SUNDARARAJAN A, et al. Defending mechanisms for protecting power systems against intelligent attacks[C]// Proceedings of 2015 10th System of Systems Engineering Conference, May 17-20, 2015, San Antonio, USA: 12-17.

[27] 刘吉臻,李明扬,房方,等.虚拟发电厂研究综述[J].中国电机工程学报,2014,34(29):5103-5111.

LIU Jizhen, LI Mingyang, FANG Fang, et al. Review on virtual power plants[J]. Proceedings of the CSEE, 2014, 34(29): 5103-5111.

[28] KOKIOPOULOU E, FROSSARD P. Polynomial filtering for fast convergence in distributed consensus[J]. IEEE Transactions on Signal Processing, 2016, 7(1): 342-354.

[29] LIU Y, XIN H, QU Z, et al. An attack-resilient cooperative control strategy of multiple distributed generators in distribution networks[J]. IEEE Transactions on Smart Grid, 2016, 7(6): 2923-2932.

[30] KERSTING W H. Radial distribution test feeders[J]. IEEE Transactions on Power Systems, 1991, 6(3): 975-985.