面向产品投产比例的多Hoist调度研究
2018-05-23毛永年唐秋华张利平
毛永年,唐秋华,张利平
1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081; 2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081)
Hoist(行车)调度问题[1]来源于以制造印刷电路板为代表的电镀企业,其产品通常需要经历多个工作站(镀槽),工件在这些工作站中的处理时间有一定的变动范围(即时间窗口)。加工时间较长的工艺阶段常配有多个功能相同的工作站,以消除此阶段的生产瓶颈,提高系统整体加工效率。同时,为了克服由运输设备造成的生产瓶颈,在同一条轨道上通常安装有多个Hoist以协同完成线上运输作业,受计算机编程控制的Hoist必须在给定的时间窗口内,将工件从当前工作站转移到下一工序所在工作站。自动化电镀生产线一般采用周期性生产模式,Hoist在每一个生产周期内执行相同的搬运作业序列以完成大批量工件的生产。此外,电镀企业常常需要将多种不同类型产品按照一定的比例投产才能达到设计产能,实现较高的设备使用率,加快订单的响应速度。因此,面向产品投产比例的调度模式在电镀生产线上应用较广泛。
针对Hoist调度问题的研究主要集中在周期性调度领域。Phillips等[2]提出了该问题的第一个周期性调度模型。Liu等[3]构建一个混合整数线性规划(MILP)模型,以解决存在重入工艺和并行工作站的周期性调度问题。Lei等[4]指出,在一个生产周期内同时加工多个工件可以提升系统的平均产出,这种模式被称为“多度周期调度”(multi-degree cyclic scheduling)。Zhou等[5]建立了解决该类问题的MILP模型。El Amraoui等[6]研究由工件加工时间窗口带来的生产瓶颈问题,提出了考虑并行工作站的MILP模型,其在一个生产周期内只涉及两个不同类型的工件。Zhao等[7]研究基于产品投产比例的单Hoist调度问题,考虑了并行工作站使用能力约束。
增加Hoist的数量可以显著提高电镀生产线的生产效率。Yang等[8]将电镀生产线划分为若干个互不重叠的区域,且每个Hoist只负责一个区域内的搬运作业,然后使用模拟退火算法求解最佳区域划分方法。Leung等[9]提出了多Hoist周期性调度问题的MILP模型。针对具有双向工件运输流的电镀生产线,Jiang等[10]分析了多类Hoist避碰条件,构建了该问题的MILP模型并发展了基于混合整数规划的分支定界算法。针对多Hoist多度周期调度问题,Li等[11-12]也采用区域划分的方法构建MILP模型。
最近,Mao等[13]研究了运行区域存在重叠的多Hoist多度周期调度问题,构建了工件流为单向情形时的最优化MILP数学模型。基于该研究,本文将问题扩展到考虑产品投产比例的多工件调度领域,即在一个周期内考虑多个具有相同工艺路线的工件,区别于文献[13],本文研究的各工件的加工时间窗口参数可能相同也可能不同,各类型工件有一定的投产比例,并且加工时间较长的瓶颈工序配有并行工作站。针对此类实际生产问题,本文采用启发式策略实现多个不同类型工件在并行工作站上的分配,进而构建混合整数规划模型。该模型同时考虑时间窗口约束、工作站使用能力约束和Hoist无碰撞约束。最后,以某印刷电路板制造企业的生产实例验证所建数学模型的应用价值。
1 问题描述与符号定义
本文研究如图1所示的电镀生产线,包括H个Hoist、n+ω个镀槽。在镀槽上方的轨道上,多个Hoist同时运行,Hoist的编号从左至右依次为1,2,…,H;工作站的编号从左至右依次为0,1,2,…,n+ω,其中工作站0同时为装载站和卸载站,各镀槽呈线性排列,镀槽n至n+ω具有相同的工艺处理功能,即参数ω为线上并行工作站的数量。每个工件自工作站0进入生产线,依次经历n个处理工序后,从工作站0离开,因此,每个工件包含n个工艺处理阶段。装载站和卸载站的容量设为无限大,工作站1至n+ω为单工件处理能力机器,即在任何时候最多只能同时加工一个工件。由于工作站之间没有缓冲设施,工件在满足时间窗口约束条件下完成当前阶段的加工后,须由Hoist将其从当前工作站取出,并运送到下一阶段所在的工作站。
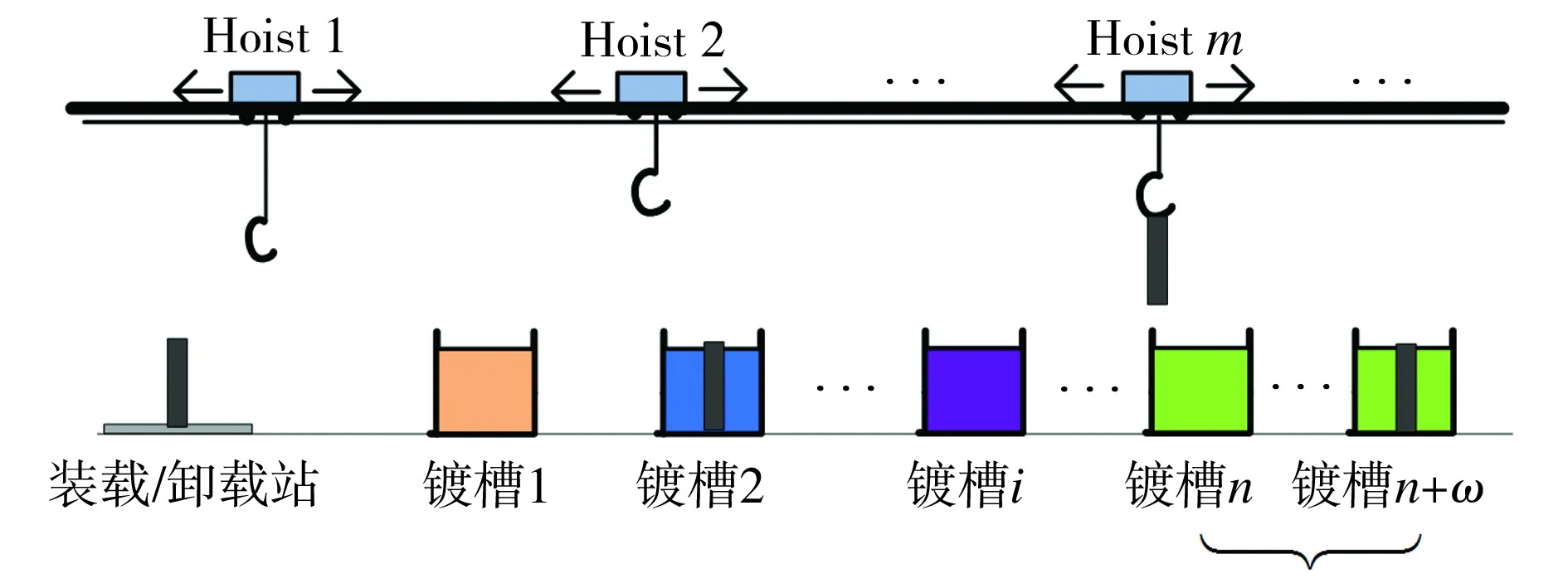
图1 典型的电镀生产线布局

由于所研究的各类型工件具有相同的工艺路线,本文根据进入时间的先后顺序将周期内的各工件依次编号为1,2,…,K。因此,面向产品投产比例的多Hoist调度问题可以用3个输入参数n、H、K来描述。
为了方便模型的表述,定义如下参数:
(1)mk,i:工件k的第i个阶段所在的工作站编号,1≤k≤K,0≤i≤n+1。
(2)搬运作业[k,i]:工件k完成第i个阶段的加工后,Hoist将工件从当前工作站取出,然后将其搬运到第i+1个阶段所在工作站,并卸载到该工作站上的全过程,1≤k≤K,0≤i≤n。
(3)Ci:加工第i个工艺阶段所能使用的工作站总数量。
(4)ak,i:工件k的第i个阶段的加工时间下限,1≤i≤n。
(5)bk,i:工件k的第i个阶段的加工时间上限,1≤i≤n。
(6)dk,i:执行搬运作业[k,i]所需的时间,其中包括Hoist将工件从工作站mk,i中取出的时间μ、Hoist将工件k从工作站mk,i运输到mk,i+1所需的时间,以及Hoist将工件k放入工作站mk,i+1的时间η,1≤k≤K,0≤i≤n。
(7)φ([k,i],[r,j],θ):当搬运作业[k,i]的优先级高于搬运作业[r,j]时,执行此两项搬运作业的最小间隔时间,其中θ=g-h,1≤h、g≤H,1≤k、r≤K,0≤i、j≤n,h与g分别为执行搬运作业[k,i]与[r,j]的Hoist编号。参数φ([k,i],[r,j],θ)用以避免Hoist之间的潜在碰撞冲突,其推导过程请参阅文献[10]和文献[13]。
(8)M:足够大的正数;ε:足够小的正数。
该问题的决策变量为:
(1)T:周期长度。
(2)sk,i:搬运作业[k,i]的开始时间,1≤k≤K,0≤i≤n。
(3)∂k,i:工件k的第i个阶段所使用的机器数量,1≤k≤K,1≤i≤n。
(4)zk,i,h:
1≤k≤K, 0≤i≤n, 1≤h≤H。
(5)yk,i;r,j:
1≤k、r≤K, 0≤i、j≤n。
2 混合整数规划模型的建立
面向产品投产比例的多Hoist调度混合整数规划模型构建如下:
minT
s.t.:
sk,i≥0, 1≤k≤K,1≤i≤n
(1)
sk,i+ε≤T, 1≤k≤K,1≤i≤n
(2)
s1,0=0
(3)
(4)
yk,i;r,j+yr,j;k,i=1, 1≤k、r≤K,1≤i (5) sr,j-sk,i≥φ([k,i],[r,j],g-h)- M(3-yk,i;r,j-zk,i,h-zr,j,g), 1≤i (6) sk,i-sr,j≥φ([r,j],[k,i],h-g)- M(2+yk,i;r,j-zk,i,h-zr,j,g), 1≤k、r≤K, 1≤i (7) sr,j+T-sk,i≥φ([k,i],[r,j],g-h)- M(2-zk,i,h-zr,j,g), 1≤k、r≤K, 1≤i (8) sk,i+T-sr,j≥φ([r,j],[k,i],h-g)- M(2-zk,i,h-zr,j,g), 1≤k、r≤K, 1≤i (9) ∂k,i=1, 1≤k≤K,1≤i≤n,Ci=1 (10) (11) sk,i-(sk,i-1+dk,i-1)+(∂k,i-1)T≥ ak,i-M(1-yk,i-1;k,i), 1≤k≤K,1≤i≤n (12) sk,i-(sk,i-1+dk,i-1)+(∂k,i-1)T≤ bk,i+M(1-yk,i-1;k,i), 1≤k≤K,1≤i≤n (13) (sk,i+T)-(sk,i-1+dk,i-1)+(∂k,i-1)T≥ ak,i-Myk,i-1;k,i, 1≤k≤K,1≤i≤n (14) (sk,i+T)-(sk,i-1+dk,i-1)+(∂k,i-1)T≤ bk,i+Myk,i-1;k,i, 1≤k≤K,1≤i≤n (15) (16) 1≤i≤n,Ci=1 (17) 模型的目标函数是最小化周期长度T。式(1)~式(3)为初始条件,其中式(1)~式(2)限定所有搬运作业的开始时间都在周期调度域[0,T)内;式(3)规定第一个工件的第一个搬运作业始于0时刻。式(4)强调任意一项搬运作业只能分配给一个Hoist。式(5)强调任意两项搬运作业之间只有唯一的一对优先关系存在。 式(6)~式(9)是Hoist的移动能力及无碰撞约束。假设搬运作业[k,i]、[r,j]分别由编号为h、g的Hoist执行,式(6)表示,当搬运作业[k,i]优先于搬运作业[r,j]时,为了保证此两项搬运作业不冲突,其开始时间间隔sr,j-sk,i必须不小于参数φ([k,i],[r,j],θ);式(7)表示,当搬运作业[r,j]优先于搬运作业[k,i]时,为了保证此两项搬运作业不冲突,其开始时间间隔sk,i-sr,j必须不小于参数φ([r,j],[k,i],-θ)。式(8)和式(9)确保了相邻周期之间的Hoist移动轨迹具有连续性且不存在碰撞冲突。 式(10)、式(11)为工件在工作站上的分配约束。对于那些不存在并行工作站的工艺阶段i,即Ci=1,式(10)表示每个工件k的每一个处理阶段只有相同的一个工作站可以分配。对于那些存在并行工作站的工艺阶段i,即Ci>1,式(11)表示分配处理工件的工作站数量不大于处理该阶段的工作站数量总和。 式(12)~式(15)为工件各阶段的加工时间窗口约束。此时根据是否存在并行工作站分两种情形讨论: (1)Ci=1。当yk,i-1;k,i=1时,工件k第i个阶段的加工都在一个周期内完成,因此其加工时长为sk,i-(sk,i-1+dk,i-1),式(12)、式(13)表示工件k第i个阶段的加工时长不小于其允许的下限值ak,i同时不大于上限值bk,i。当yk,i-1;k,i=0时,工件k第i个阶段的加工开始时间要晚于其结束时间,这意味着工件k第i个阶段的加工跨越了两个周期,那么工件k第i个阶段的实际加工时长为(sk,i+T)-(sk,i-1+dk,i-1)。式(14)、式(15)确保此种情形下工件的加工时间窗口约束。 (2)Ci>1。在整个周期内定有(∂k,i-1)个工作站被工件k完全占用,此时可视为工件k的第i个阶段已经加工了(∂k,i-1)个周期。因此,相对于Ci=1时的情形,Ci>1时工件k的第i个阶段存在额外的(∂k,i-1)个周期的加工时长。 式(16)~式(17) 为工作站使用能力约束。根据式(10)、式(11)可知,当Ci=1时,一个周期内多个工件共享一个工作站,此时工作站可能存在使用能力冲突;当Ci>1时,一个周期内每个工作站至多加工一个工件,此时不存在工作站使用冲突。因此,只需考虑第一种情形(Ci=1)对工作站使用能力约束进行建模。文献[5]中已构建了单Hoist多度周期调度问题的工作站使用能力约束,而文献[13]又将问题扩展至多Hoist多度周期调度领域。本文研究具有与上述研究相同的工艺路线且不存在重入工艺,针对式(16)、式(17)的详细解释请参阅文献[5]和文献[13]。 本文研究的实例来自于某印刷电路板制造企业。一般而言,印刷电路板需要经历3个电镀工艺环节:沉铜电镀、全板电镀、图形电镀。下面针对该企业的全板电镀生产过程进行实例分析。 该企业全板电镀生产线的工艺流程如图2所示。工件(印刷电路板)首先在1号工位(缸号1)上板,随后经历7个工艺阶段,包括除油(缸号5)、水洗1(缸号6)、水洗2(缸号7)、酸洗(缸号10)、镀铜(缸号11~25)、水洗3(缸号9)、高位水洗1(缸号8),最后,在1号工位下板。但是由于夹具(企业称之为“飞巴”)在卸载工件后需要经过退镀工艺环节(包括退镀、水洗4、高位水洗2)后返回1号工位,因此,全板电镀工艺必须以夹具为研究对象。此外,为了避免工件表面黏附的电镀液污染其它镀槽,Hoist将工件从电镀液中取出后还要停留一段时间(滴水时间),待工件表面的液体滴尽之后再开始移动。 图2 全板电镀工艺流程 本文研究该企业三种常见的工件类型,分别记为工件A、B、C,各工艺阶段加工时间在表1中列出。除了镀铜工艺之外,A、B、C三种产品的其它工艺加工时间相同。 表1 各工件的加工时间窗口 其它输入参数设置如下:Hoist空载移动速度χ=0.50 m/s,负载移动速度v=0.50 m/s。Hoist装载和卸载工件的时间μ=η=8 s。全板电镀生产线每个工作站间隔1 m,Hoist之间的安全距离为1 m。 在CPU主频为2.30 GHz的PC机上使用C++语言编写数学模型代码,并在Visual Studio 2010软件平台上调用优化软件IBM ILOG CPLEX(版本12.7)求解数学模型。该案例的求解结果如表2~表7所示,其中“—”表示在当前参数设置下问题无可行解。 表2给出了各类型工件单独生产时,最优周期长度T与镀铜工位使用数量(C5)的关系。总的来说,使用的镀铜工位数量越多,周期长度越短。考虑到工件A镀铜工序的加工时间参数,当镀铜工序使用8个镀槽时,该线上的生产能力已经饱和,继续增加镀铜工位不会缩减周期长度,因此剩余7个镀槽始终为空闲状态。 表2工件单独生产时的最优周期长度T Table2OptimalcycleTwhenthepartsareproducedindependently C5T/s工件A工件B工件C12344534471444587.51337.51787.58328670.25895.259—596.4796.44410—536.8716.811—488.36465212—447.667597.66713—413.5355214—384512.57115—358478 为了提高电镀槽的使用率,考虑将工件A分别与工件B及工件C联合生产,应用所建模型分别进行求解。表3和表4列出了这两种情形下镀铜工位所有可能的分配组合以及对应的最优周期长度T。观察结果可知,当工件A与B同时生产时,工件A使用4个镀铜槽、工件B使用9个镀铜槽可以实现最小的生产周期656 s;当工件A与C同时生产时,工件A使用4个镀铜槽、工件C使用11个镀铜槽可以实现最小的生产周期656 s,此时,所有的镀铜工位都被使用,使用率达到最高。 表3工件A与B同时生产时的最优周期长度T(单位:s) Table3OptimalcycleTwhenpartAandpartBareproducedsimultaneously 工件B使用的镀槽数量工件A使用的镀槽数量123415372———22682———323501790——4—1343——5—11751074—6——895—7——8957618——7836719———656 表4工件A与C同时生产时的最优周期长度T(单位:s) Table4OptimalcycleTwhenpartAandpartCareproducedsimultaneously 工件C使用的镀槽数量工件A使用的镀槽数量123423584———323892389——423441792——5—1434——6—11951195—7—11721024—8——896—9——79679610——78171711———656 图3给出了工件A与C按1∶1同时投产时的调度方案。由图3可知,各Hoist移动轨迹安排合理,每个搬运作业执行紧凑。调度周期内,一个工件A和一个工件C分别在0、328 s进入生产线。一个工件A和一个工件C分别在192、64 s离开生产线。在192 s离开的工件A是4个周期前进入该线并在此周期完成所有处理工序。在64 s离开的工件C是11个周期前进入该线并在当前周期完成所有处理工序。工件A离开生产线时夹具立即返回生产线执行退镀操作。工件C 图3 工件A与C同时生产时的调度方案 Fig.3SchedulingsolutionwhenpartAandpartCareproducedsimultaneously 离开生产线后,Hoist立即运送一个完成退镀工艺的夹具离开系统。一个周期内总有两个夹具随工件进入系统,并且有两个夹具独立完成退镀工艺后等待装夹工件。系统稳态运行时,生产线按照比例1∶1产出工件A与C。 此外,本文还研究了该生产线按照比例2∶1生产工件A与B以及A与C时的情形,其求解结果见表5、表6。针对工件A与B的组合生产,获得了2组可行的镀铜工位分配方案,最优调度方案可以在一个周期内使用12个镀铜工位,其对应的最优周期长度为984 s。针对工件A与C的组合生产,获得了3组可行的镀铜工位分配方案,最优调度方案可以在一个周期内使用14个镀铜工位,其对应的最优周期长度同样为984 s。两种最优方案稳态运行时,按照2∶1的比例产出工件。 表5工件A与B的投产比例为2∶1时的求解结果 Table5ResultsforthecombinationofpartAandpartBwithproductionratioof2∶1 镀铜工位分配方案镀铜工位使用数量AABT/s133510742336984 表6工件A与C的投产比例为2∶1时的求解结果 Table6ResultsforthecombinationofpartAandpartCwithproductionratioof2∶1 镀铜工位分配方案镀铜工位使用数量AACT/s13361197233710243338984 表7给出了工件A、B、C按照不同比例投产时镀铜工位的使用数量、周期长度以及模型的求解时间。当工件投产数量比为2∶1∶1时,其对应的最优周期长度为1352 s。此时,一个周期内2个工件A总计使用4个镀铜工位,工件B和工件C分别使用5个和6个镀铜工位,即15个镀铜工位全部被使用。该方案稳态运行时,每1352 s按比例产出4个工件,而当各工件单独生产时,每产出这4个工件平均需要328×2+358+478=1492s。因此,相对于各工件单独生产,按2∶1∶1联合投产模式可以获得9.38%的产出提升率。当工件的投产数量比为1∶2∶1时,同样使用了全部15个镀铜工位,其产出提升率为5.76%。当工件的投产数量比为2∶1∶3时,使用了14个镀铜工位,其产出提升率为2%。 表7工件A、B、C不同投产比例时的求解结果 Table7ResultsforthecombinationofpartA,partBandpartCwithdifferentproductionratios 投产比例(A∶B∶C)镀铜工位使用数量ABCT/s求解时长/s2∶1∶12×21×51×61352791∶2∶11×22×41×51439952∶1∶32×11×33×32399170 需要强调的是,在实际生产中,凭借工作经验、人工拼凑制定的调度方案往往不具有最优性,而使用本文所提出的模型可以快速获得问题的最优调度方案。更为重要的是,生产企业可以根据订单需求,利用本文方法研究适合企业的产品投产比例。这不仅可以加快订单响应速度,还可以提高生产效率。 本文将多Hoist多度周期调度问题拓展至多工件类型集成调度领域,构建了面向产品投产比例的多Hoist调度问题的混合整数规划模型,该模型基于工件所使用的并行工作站数量建立加工时间窗口约束,简化了存在并行工作站时的使用能力约束建模。通过对实际生产案例的研究表明,多工件调度可以提高加工设备使用率,而面向产品投产比例的调度模式可以更加灵活地应对多样化的实际生产需求。 参考文献 [1] Manier M A, Bloch C. A classification for hoist scheduling problems[J].International Journal of Flexible Manufacturing Systems,2003,15(1):37-55. [2] Phillips L W, Unger P S. Mathematical programming solution of a hoist scheduling program[J]. AIIE Transactions, 1976,8(2):219-225. [3] Liu J Y, Jiang Y, Zhou Z L. Cyclic scheduling of a single hoist in extended electroplating lines: a comprehensive integer programming solution[J]. IIE Transactions, 2002,34(10):905-914. [4] Lei L, Wang T J. Determining optimal cyclic hoist schedules in a single-hoist electroplating line[J]. IIE Transactions, 1994,26(2):25-33. [5] Zhou Z, Che A D, Yan P Y. A mixed integer programming approach for multi-cyclic robotic flowshop scheduling with time window constraints[J].Applied Mathematical Modelling,2012,36(8):3621-3629. [6] El Amraoui A, Manier M-A, El Moudni A, et al. Resolution of the two-part cyclic hoist scheduling problem with bounded processing times in complex lines’ configuration[J]. European Journal of Industrial Engineering, 2012,6(4):454-473. [7] Zhao C Y, Fu J, Xu Q. Production-ratio oriented optimization for multi-recipe material handling via simultaneous hoist scheduling and production line arrangement[J]. Computers and Chemical Engineering, 2013,50(7):28-38. [8] Yang Guangwen, Ju Dapeng, Zheng Weimin, et al. Solving multiple hoist scheduling problems by use of simulated annealing[J].软件学报,2001,12(1):11-17. [9] Leung J M Y,Zhang G Q,Yang X G,et al. Optimal cyclic multi-hoist scheduling: a mixed integer programming approach[J].Operations Research,2004, 52(6):965-976. [10] Jiang Y,Liu J Y. A new model and an efficient branch-and-bound solution for cyclic multi-hoist scheduling[J].IIE Transactions, 2014,46(3):249-262. [11] Li X, Fung R Y K. Optimal multi-degree cyclic solution of multi-hoist scheduling without overlapping[J]. IEEE Transactions on Automation Science and Engineering, 2017, 14(2):1064-1074. [12] LiX, ChanFTS, ChungSH. Optimalmulti-degree cyclic scheduling of multiple robots without overlapping in robotic flowshops with parallel machines[J]. Journal of Manufacturing Systems, 2015, 36:62-75. [13] Mao Y N, Tang Q H, Li Z X, et al. Mixed-integer linear programming method for multi-degree and multi-hoist cyclic scheduling with time windows[J]. Engineering Optimization, 2018:1-18. DOI:10.1080/0305215X.2017.1418865.3 实例研究
3.1 工艺介绍
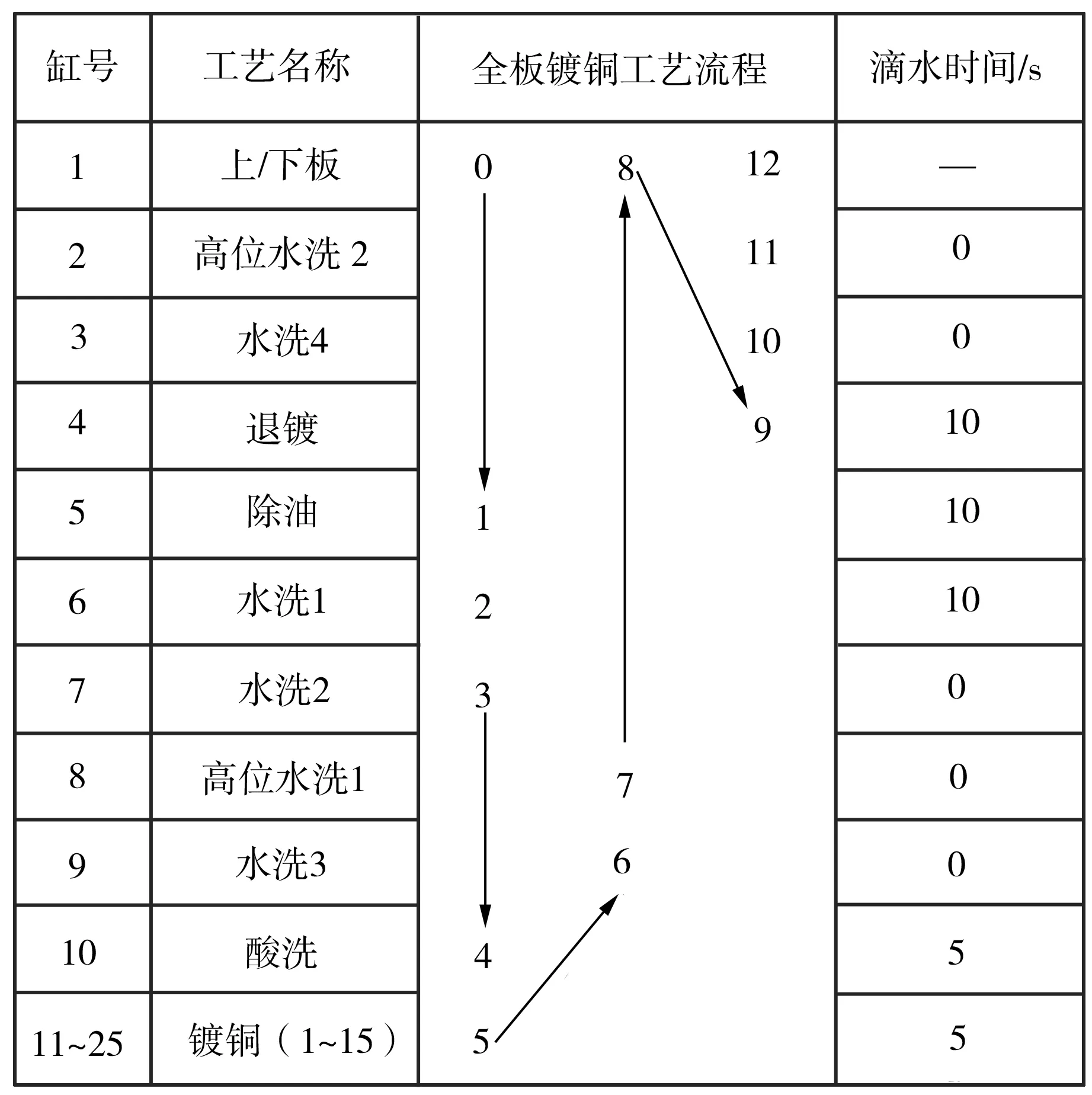
3.2 输入参数
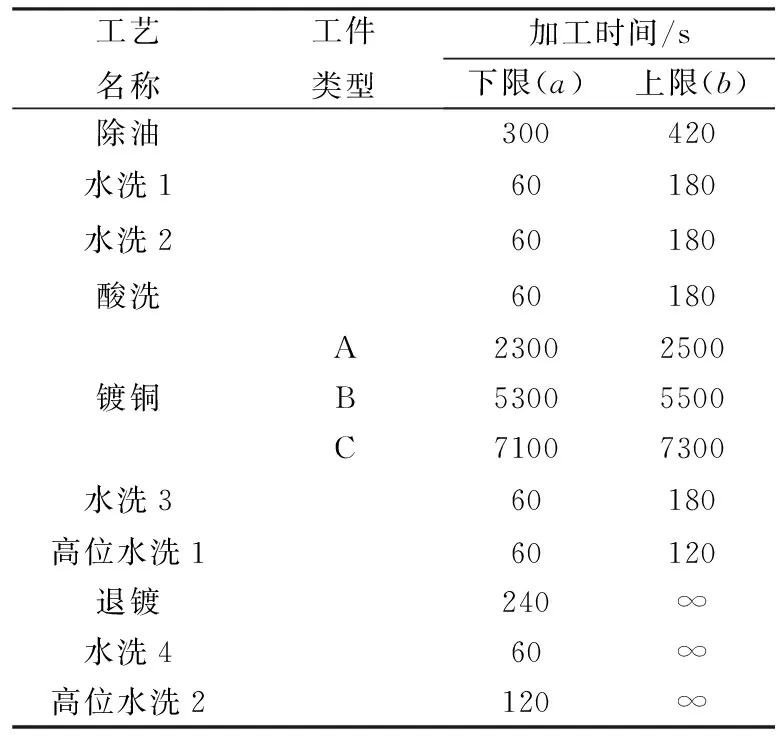
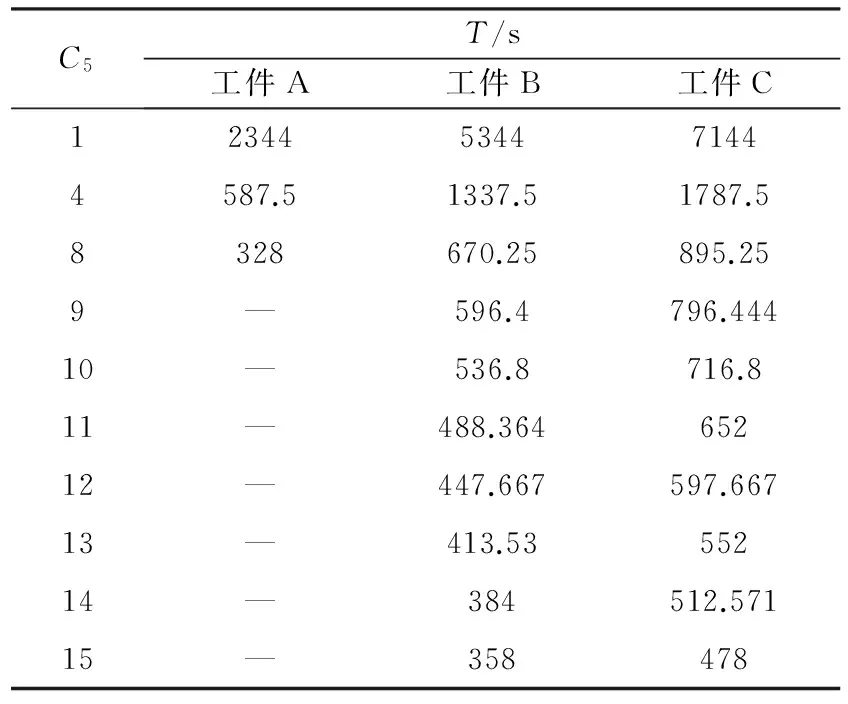
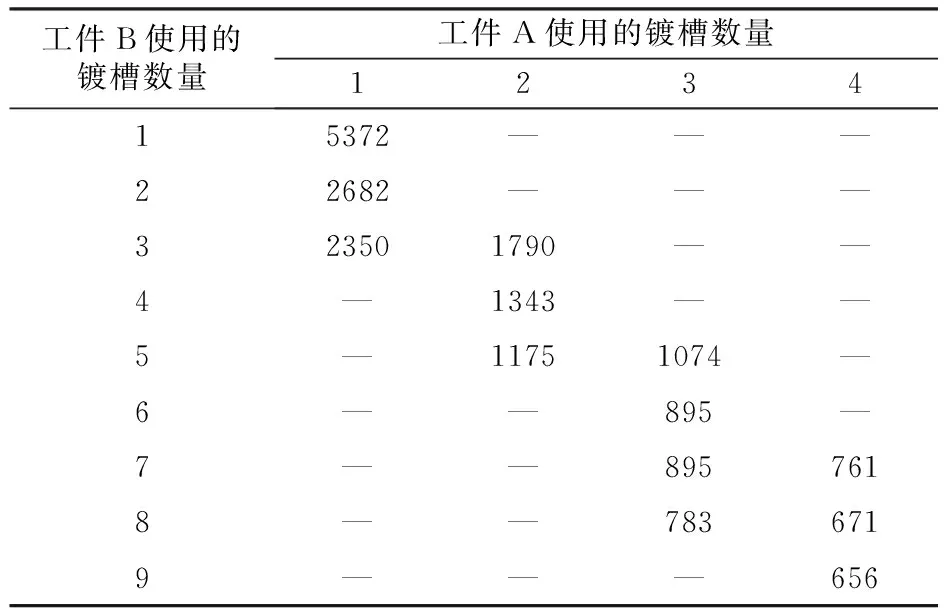
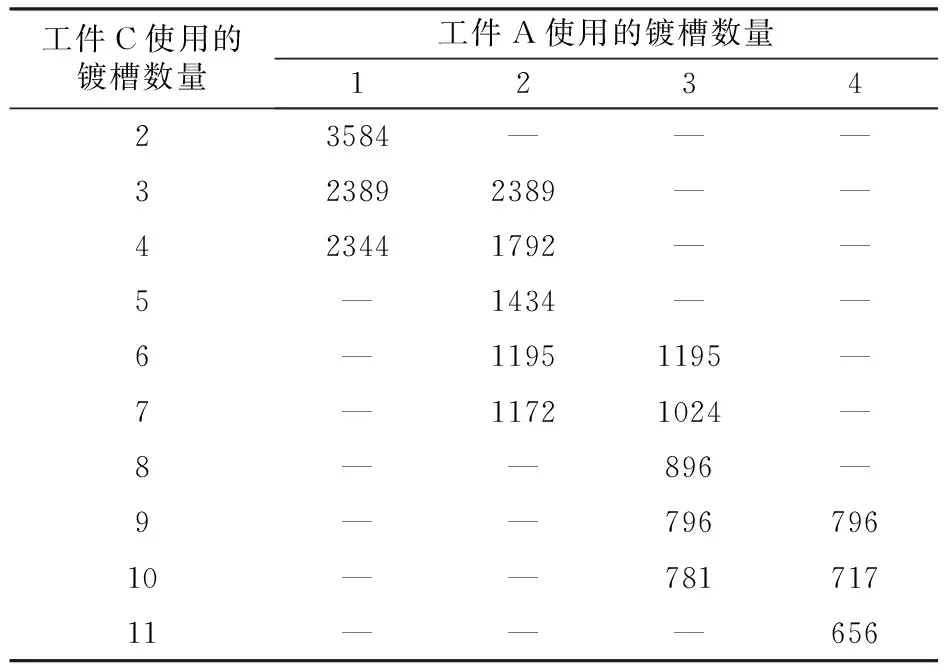
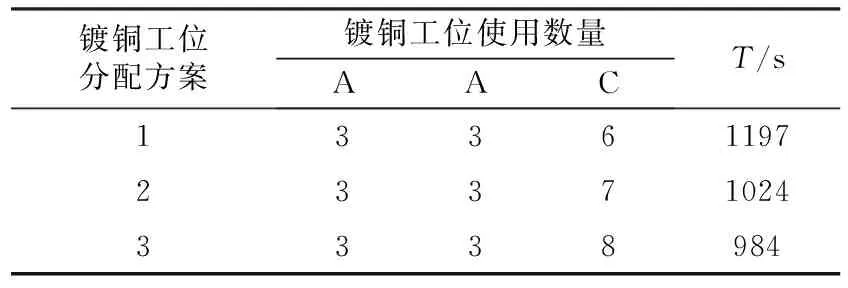
3.3 案例求解



4 结语
