悬臂输流单层碳纳米管的颤振失稳分析

李 明，方 康，郑华升

(武汉科技大学冶金工业过程系统科学湖北省重点实验室，湖北 武汉，430065)

碳纳米管(CNT)具有完美空心圆柱形几何结构，已成为纳米尺度下流体储藏与输运的重要载体，广泛应用于生物医药领域(如抗肿瘤药物的靶向输送)以及纳机电系统(NEMS)中[1-3]，与之相应的输流碳纳米管动力学特性也吸引了国内外研究者的大量关注。在这些研究中，非局部连续介质弹性理论作为一种分析手段亦已获得较为广泛的认可。Wang等[4]应用非局部欧拉-伯努利(Euler-Bernoulli)梁模型研究了输流双层碳纳米管的固有频率和屈曲失稳特性，发现了小尺度参数对其振动频率的影响。Lee等[5]利用非局部弹性理论研究了固支载流单层碳纳米管(SWCNT)的振动问题。此类研究结果综合表明，随着小尺度的增加，碳纳米管的振动频率会降低，在管内流体高速及高阶时更为明显。

然而，已有的相关研究多半针对两端具有支撑的输流碳纳米管动力学特性，对悬臂状况下输流碳纳米管的振动失稳特性研究较少。不同于其它边界情况，悬臂输流管道系统是一个非保守系统[6]，这意味着管道、流体之间耦合系统的能量将随时间而发生变化，管内流速较小时，流体对管道所做的功为负，但随着管道内流体流速的增加，流体作用在管道上的功可能为正，由此管道将从流体中吸收能量，在流速达到临界流速时会通过一个Hopf分岔发生颤振，造成系统的动态失稳，大量针对非微尺度、纳米尺度管道系统的研究已对这一特性做过多方面的探讨[7-8]。此外，管道自身的黏弹性特性在输流管振动中也是一个需要考虑的重要因素[9]。本文以非局部弹性理论为基础，采用欧拉-伯努利梁模型，考虑碳纳米管的小尺度效应以及碳纳米管的黏弹性特性，着重研究悬臂输流单层碳纳米管的颤振失稳问题。

1 振动控制方程与边界条件

图1所示为悬臂输流单层碳纳米管，其长度为L，外径为D，横截面积为A，弯曲刚度为EI，E为材料弹性模量，材料的黏弹性特性采用Kelvin-Voigt模型；每单位长度上纳米管的质量和内部流体的质量分别为mc和mf；流体流速不变且为U。振动中假定管道只发生横向面内振动，且不考虑重力以及管道外部拉、压力的影响。W(X,T)为纳米管振动的横向位移，其中，X为沿纳米管的轴向坐标，T为时间。

图1 悬臂输流单层碳纳米管

Fig.1Cantileverfluid-conveyingsingle-walledcarbonnanotube

输流SWCNT系统的总动能为

(1)

系统的应变能为

(2)

式中：εXX及σXX分别为X方向的应变及应力。

在小变形情况下，Euler-Bernoulli梁应变-位移关系为：

(3)

根据材料黏弹性本构关系[10]及非局部弹性理论，SWCNT应力-应变关系可表示为：

(4)

式中：e0a是纳米材料中引起结构小尺度效应的参数，E*为材料的黏弹性阻尼系数。

考虑到弯矩M与应力σXX的关系式：M=∬σXXZdA，应用哈密顿原理：

(5)

可以得到输流纳米管的运动方程为：

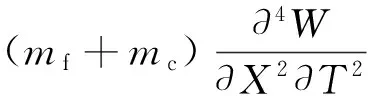
(6)

对于悬臂输流纳米管，考虑边界小尺度因素，其边界条件为：

X=L：

(7)

2 振动控制方程求解

微分变换法(DTM)是一种基于泰勒级数展开的半解析计算方法[11]，相较于Galerkin法、微分求积法(DQM)、有限元法(FEM)等，可以更精确而简单地对高阶偏微分方程进行求解，且随着方程阶数的增加，其求解过程并不会变得繁琐，DTM法部分基本运算法则如表1所示。

表1 微分变换法部分基本运算法则

本文将DTM法推广到纳米级别输流管系统的振动稳定性分析中，利用该法对上述高阶偏微分方程在悬臂边界条件下进行求解。为便于后续的数值计算与分析，本文引入下列无量纲化的变量和参数：

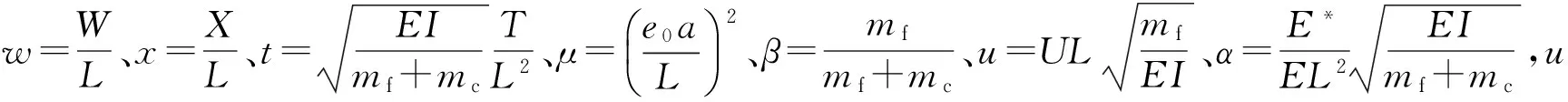
(8)

以及无量纲悬臂边界条件

x= 1：

(9)

(10)

基于DTM运算法则，可得到方程(10)的微分变换形式

[1-μu2](k+4)!Φ(k+4)+u2(k+2)!Φ(k

(11)

其相应的悬臂边界条件的微分变换形式

Φ(0)=Φ(1)=0

(12)

[αk(k-1)(k-2)-

(13)

令Φ(2)=C1,Φ(3)=C2，进而与式(12)一起代入式(11)，迭代求得Φ(k)，k=4,5,…,N,然后将Φ(k)，k=1,2,…,N代入式(13)，可得到以下方程：

(14)

其中aij是关于Ω0和其它系统参数的多项式，上式有平凡解的条件是其系数矩阵行列式为零，考虑Ω0=iΩ，即可获得系统的无量纲复频率Ω，其中Ω的实部Re(Ω)是系统的无量纲固有频率，其虚部Im(Ω) 与阻尼有关。已有研究表明[10]，系统的稳定性取决于Ω的虚部，如果Im(Ω)>0，系统稳定；如果Im(Ω) <0，系统不稳定。在Im(Ω)=0 时，对于悬臂纳米管系统将存在两类失稳类型：1) 若实部Re(Ω)=0，则系统将因发散而出现静态的屈曲失稳；2) 若实部Re(Ω)≠0，则系统将出现颤振表现为动态失稳。

3 系统颤振失稳分析

对于悬臂输流纳米管的颤振失稳分析，本文采用的参数为[12]：输流流体的密度ρf=1000kg/m3,碳纳米管密度ρc=2300 kg/m3，外层半径R0=3nm，壁厚td=0.1nm，弹性模量E=3.4 TPa，振动中为不计剪切变形与转动惯量[13]，长径比L/(2R0)=40，无量纲小尺度参数μ、无量纲黏弹性阻尼参数α以及无量纲质量参数β的取值在具体算例中给予说明。DTM的计算精度取决于截断项数N的取值，N的取值越大计算结果越接近精确解，本文取N=40，经验证此时已能保证前四阶模态的解足够精确。

图2、图3显示的是不同质量参数β下悬臂输流SWCNT前四阶无量纲复频率Ω的Argand图，此时小尺度参数μ=0，黏弹性阻尼参数α=0，图中各处所示数据为该处对应的无量纲流速值。由图2、图3可以看到，在不同质量参数下，管内流动流体在各阶模态中均会引起阻尼作用，且系统的各阶频率均随流速增加而降低。比较前四阶复频率Ω的变化规律可以发现，系统的第一阶模态始终不会出现颤振失稳。而当质量参数β较小时(β=0.2)，随着流速的增加，系统的第二阶模态在u=5.6时率先发生颤振失稳，其失稳时对应的流速称为系统的颤振失稳临界流速，记为ucr，即此时ucr=5.6,之后若继续增加流速，系统的第四阶模态亦会出现失稳(未示于图中)。然而，在质量参数较大(β=0.5)的系统中，可以发现系统的颤振失稳并不是在第二阶模态率先发生，此时，悬臂输流SWCNT系统的第三阶模态在流速ucr=9.3率先失稳，第二阶模态则是经历较为复杂的过程后最终失稳。以上结论与文献[10]相同，进而也验证了本文采用的DTM求解方法的正确性。另外，由图2、图3的分析可以得到，质量参数β较大时，系统的颤振失稳临界流速更高，系统更趋于稳定。

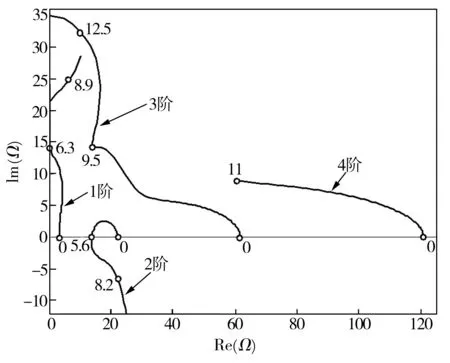
图2系统前四阶无量纲复频率实部与虚部随流速变化规律(β=0.2,μ=0,α=0)

Fig.2Thedimensionlesscomplexfrequencyofthefourlowestmodesofthecantileveredsystemasafunctionofthedimensionlessflowvelocity(β=0.2,μ=0,α=0)

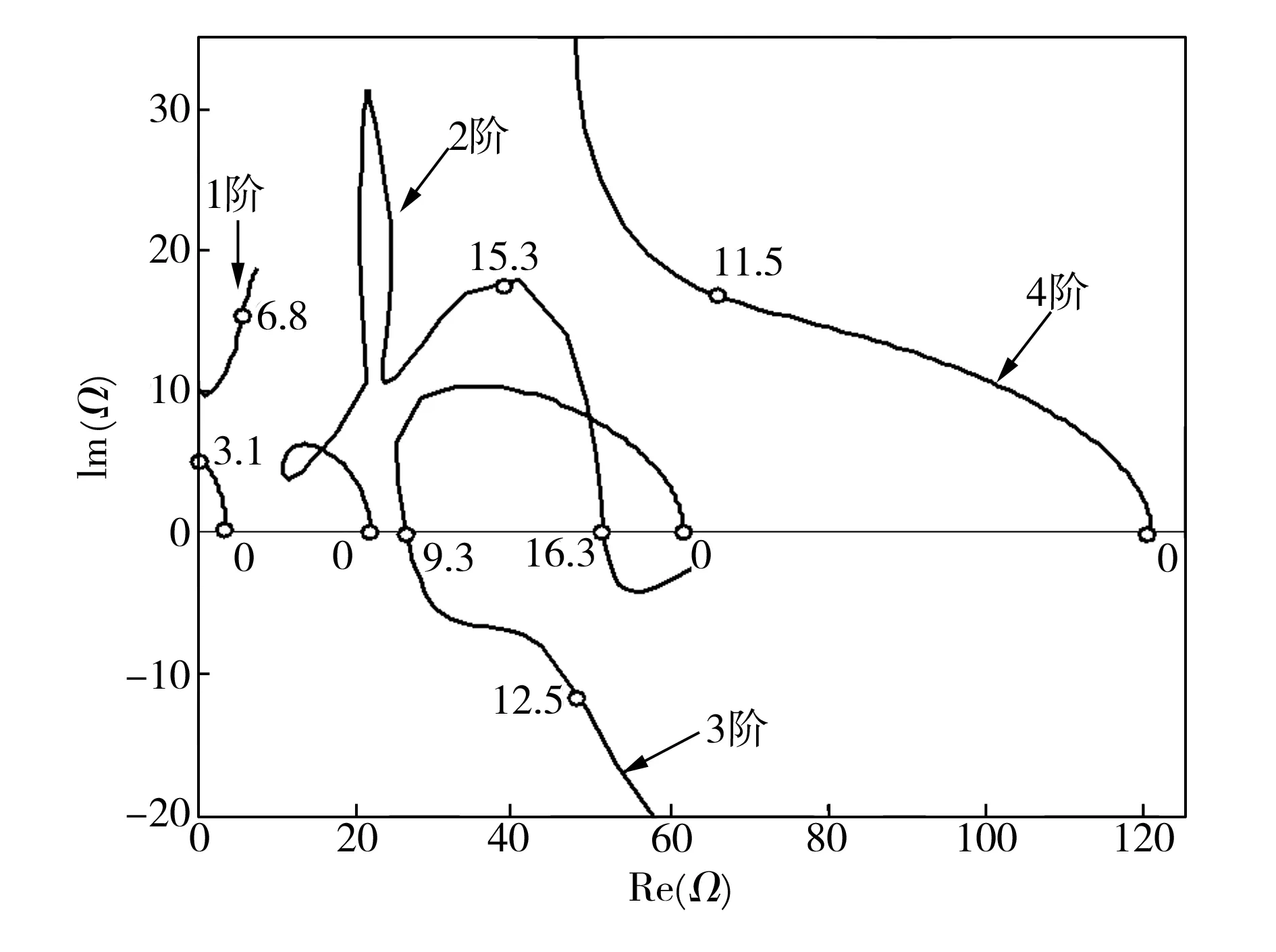
图3系统前四阶无量纲复频率实部与虚部随流速变化规律(β=0.5,μ=0,α=0)

Fig.3Thedimensionlesscomplexfrequencyofthefourlowestmodesofthecantileveredsystemasafunctionofthedimensionlessflowvelocity(β=0.5,μ=0,α=0)

图4和图5分别为不同质量参数条件下，悬臂输流纳米管考虑小尺度效应时，前四阶无量纲复频率Ω的Argand图，此时，小尺度参数μ=0.05，黏弹性阻尼参数α=0。将图4、图5与图2、图3进行比较可以看出，考虑小尺度情况下，前四阶模态随管内流体流速的变化规律保持不变。只是，在考虑小尺度效应时，系统的颤振临界流速减小(β=0.2时，二阶模态率先失稳，ucr=5.4；β=0.5时，三阶模态率先失稳，ucr=8.6)，说明小尺度效应降低了系统的稳定性，使悬臂输流系统更为柔软。从各图比较还可以得到，质量参数β越大，系统各阶模态无量纲复频率Ω的实部、虚部随流速的变化规律受小尺度效应的影响越明显。

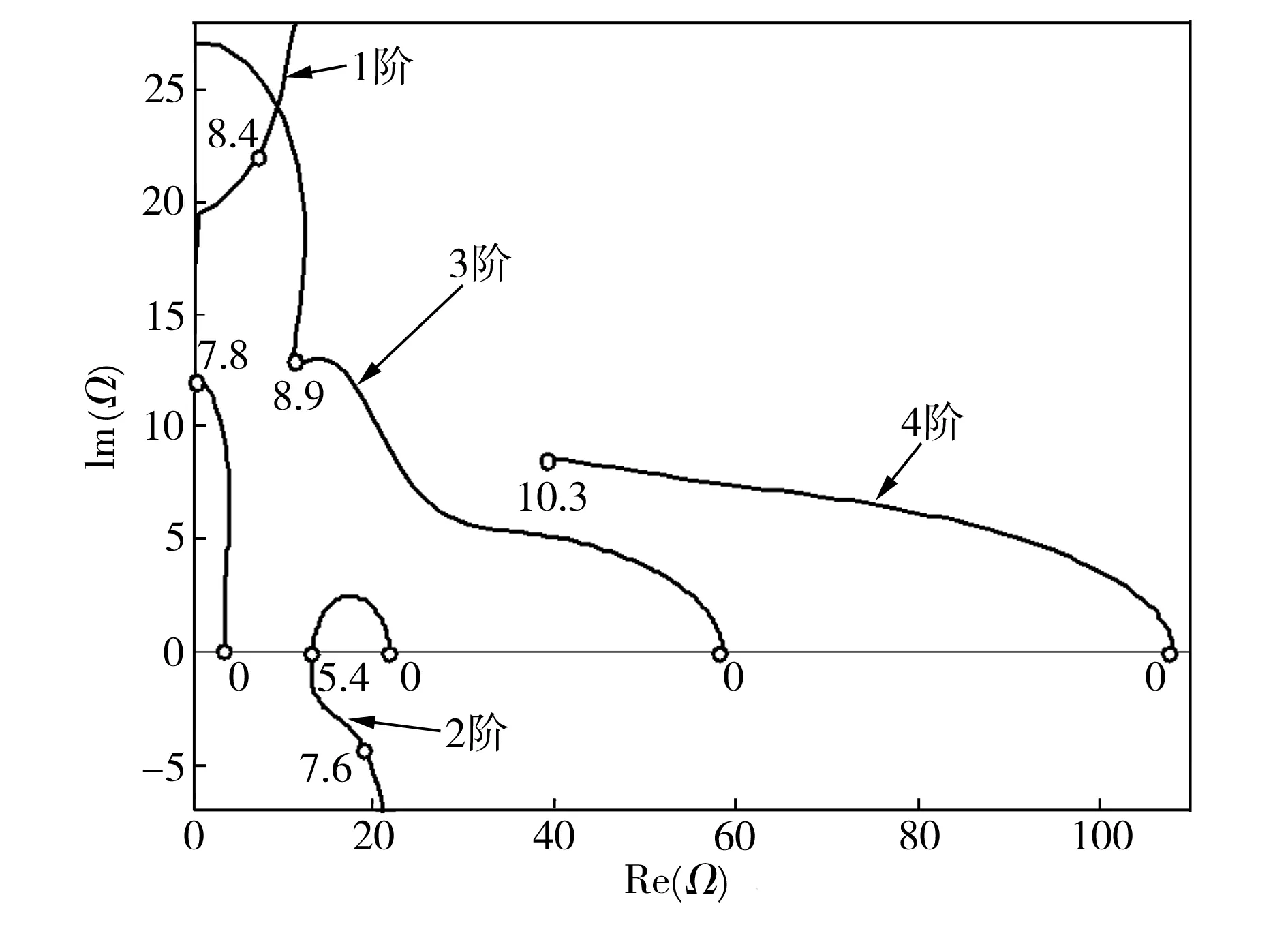
图4系统前四阶无量纲复频率实部与虚部随流速变化规律(β=0.2,μ=0.05,α=0)

Fig.4Thedimensionlesscomplexfrequencyofthefourlowestmodesofthecantileveredsystemasafunctionofthedimensionlessflowvelocity(β=0.2,μ=0.05,α=0)

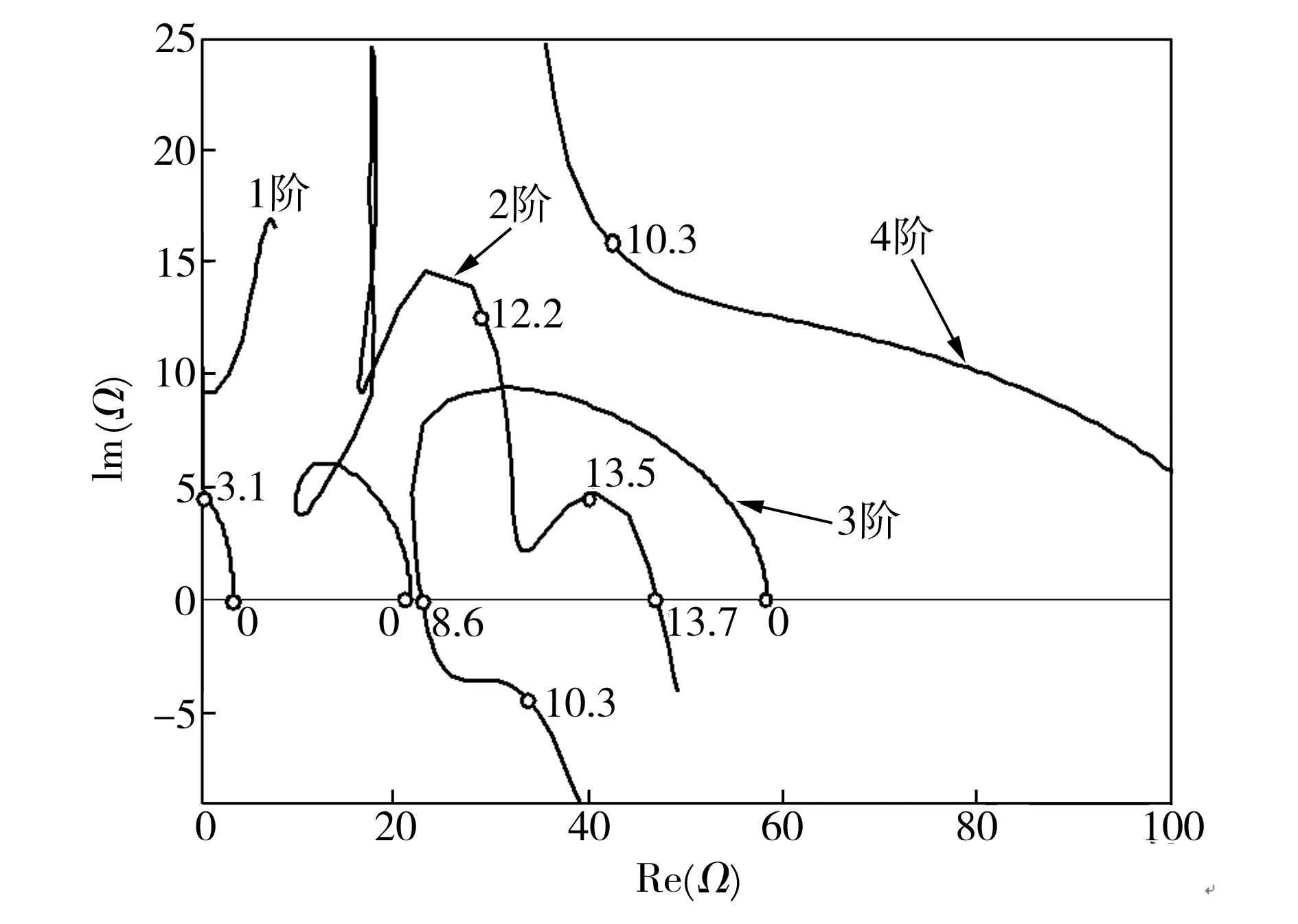
图5系统前四阶无量纲复频率实部与虚部随流速变化规律(β=0.5,μ=0.05,α=0)

Fig.5Thedimensionlesscomplexfrequencyofthefourlowestmodesofthecantileveredsystemasafunctionofthedimensionlessflowvelocity(β=0.5,μ=0.05,α=0)

图6和图7分别为不同质量参数条件下，管道黏弹性性质对悬臂输流碳纳米管系统颤振失稳的影响情况，此时黏弹性阻尼参数α均为1×10-3，小尺度参数μ均为0.05。将图6、图7与图4、图5进行比较可以发现，管道的黏弹性性质对悬臂输流管道各阶模态的影响程度不同，黏弹性阻尼参数对第一阶模态影响不大，但对其后几阶模态影响效果显著。首先，当黏弹性阻尼参数α不为0时，在管内流体流速极低时(u→0)后几阶模态已表现出较为明显的阻尼效果；其次，就黏弹性性质对系统颤振失稳的影响而言，比较上述各图可以看出，在较小的质量参数条件下，系统颤振失稳临界流速随黏弹性阻尼参数增加而升高，而在较大的质量参数条件下，系统颤振失稳临界流速则随黏弹性阻尼参数增加而降低。这就意味着管道系统储存的弹性能、管道黏弹性特性的振动耗散能以及管道由流体中的吸入能三者共同决定了悬臂输流系统的颤振失稳临界流速。

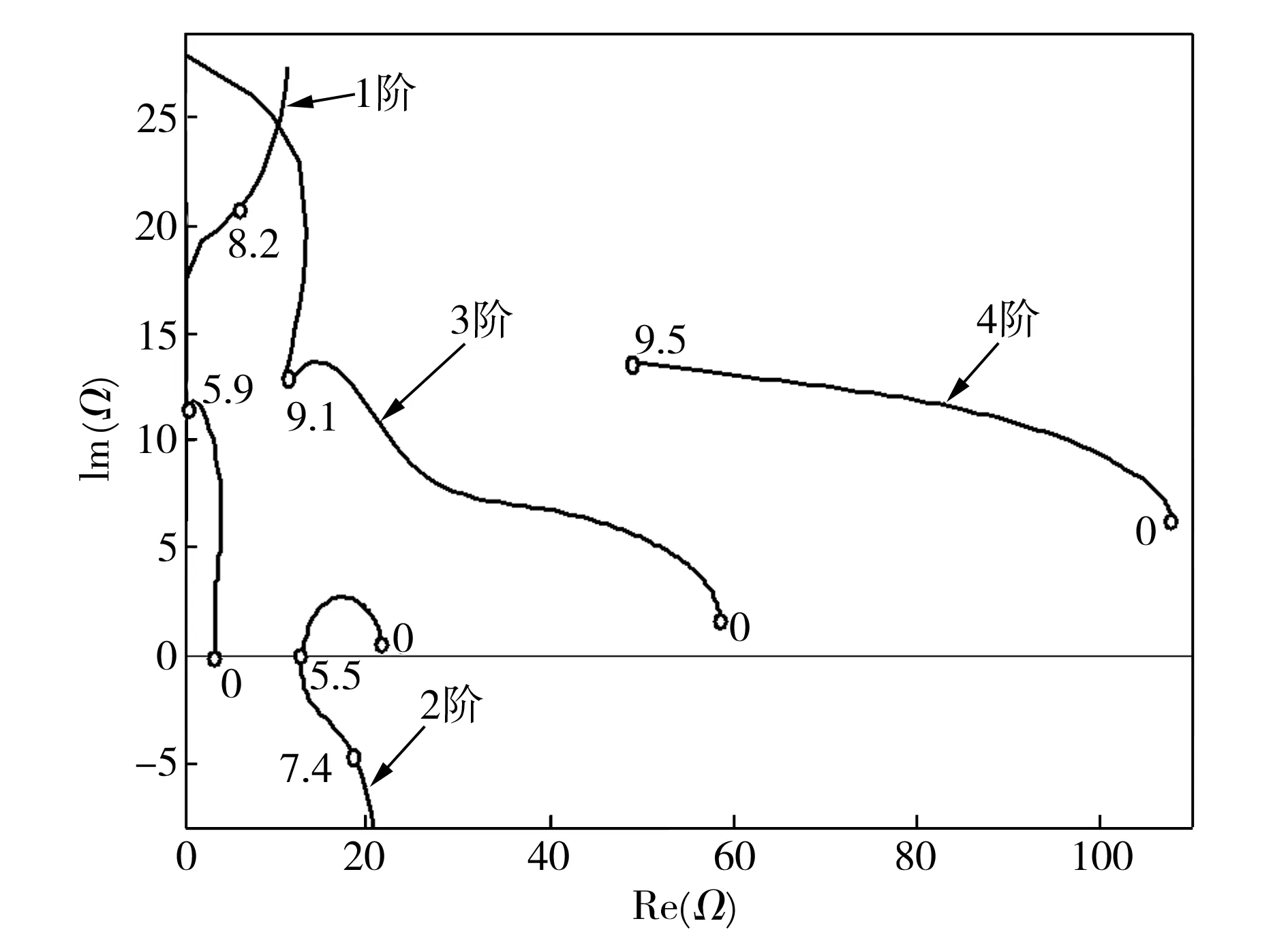
图6系统前四阶无量纲复频率实部与虚部随流速变化规律(β=0.2,μ=0.05,α=1×10-3)

Fig.6Thedimensionlesscomplexfrequencyofthefourlowestmodesofthecantileveredsystemasafunctionofthedimensionlessflowvelocity(β=0.2,μ=0.05,α=1×10-3)

图7系统前四阶无量纲复频率实部与虚部随流速变化规律(β=0.5,μ=0.05,α=1×10-3)

Fig.7Thedimensionlesscomplexfrequencyofthefourlowestmodesofthecantileveredsystemasafunctionofthedimensionlessflowvelocity(β=0.5,μ=0.05,α=1×10-3)

4 结语

本文基于非局部Euler-Bernoulli梁模型，采用DTM法对悬臂输流单层碳纳米管的高阶偏微分方程进行求解，分析了此类非保守系统的颤振失稳问题,分别讨论了系统质量参数、管道黏弹性参数以及小尺度参数对系统前四阶无量纲复频率以及系统无量纲颤振失稳临界流速的影响。结果表明输流纳米管小尺度效应将会降低系统的稳定性，使悬臂输流系统更为柔软；而管道黏弹性阻尼参数对系统颤振失稳临界流速的影响与系统质量参数相关：质量参数较小时，系统颤振失稳临界流速随黏弹性阻尼参数增加而升高，质量参数较大时，系统颤振失稳临界流速则随黏弹性阻尼参数增加而降低。本文所得结论可为工程纳米流体机械的设计分析提供一定的理论参考。

参考文献

[1] Iijima S. Helical microtubes of graphite carbon[J].Nature, 1991, 354(7):56-58.

[2] SoltaniP,FarshidianfarA.Periodicsolutionfor nonlinear vibration of a fluid-conveying carbon nanotube, based on the nonlocal continuum theory by energy balance method[J]. Applied Mathematical Modelling, 2012, 36 (8): 3712-3724.

[3] 李明，周攀峰，郑华升.纵向磁场中载流单层碳纳米管的振动与失稳[J].武汉科技大学学报，2017,40(1)：27-31.

[4] Wang L, Ni Q, Li M. Buckling instability of double-wall carbon nanotubes conveying fluid[J]. Computational Materials Science, 2008, 44(2):821-825.

[5] Lee H L, Chang W J. Vibration analysis of a viscous-fluid-conveying single-walled carbon nanotube embedded in an elastic medium[J]. Physica E, 2009, 41(4):529-532.

[6] 倪樵,王琳,黄玉盈. 吸流管道动力学模型的研究现状与展望[J].应用力学学报，2008,25(3)：450-454.

[7] Païdoussis M P, Li G X. Pipes conveying fluid:a model dynamical problem[J]. Journal of Fluids and Structures, 1993, 7(2): 137-204.

[8] 王忠民, 冯振宇, 赵凤群, 等. 弹性地基输流管道的耦合模态颤振分析[J]. 应用数学和力学，2000, 21 (10): 1060-1068.

[9] 王忠民，张战午，李会侠. 粘弹性地基上粘弹性输流管道的稳定性分析[J]. 计算力学学报，2005, 22 (5): 613-617.

[10] 齐欢欢. 输液管道颤振失稳的时滞控制[D].上海：同济大学，2009.

[11] Chen C K, Ho S H. Transverse vibration of a rotating twisted Timoshenko beams under axial loading using differential transform[J]. International Journal of Mechanical Science, 1999, 41(11): 1339-1356.

[12] Hosseini M, Sadeghi-Goughari M, Atashipour S A, et al. Vibration analysis of single-walled carbon nanotubes conveying nanoflow embedded in a viscoelastic medium using modified nonlocal beam model[J]. Archives of Mechanics, 2014, 66(4):217-244.

[13] Yoon J, Ru C Q, Mioduchowski A. Flow-induced flutter instability of cantilever carbon nanotubes[J]. International Journal of Solids and Structures, 2006, 43(11-12): 3337-3349.