岸礁地形对港内低频波浪共振影响的数值研究
2018-05-23高俊亮王志瑜周校军嵇春艳郑子波
高俊亮,王志瑜,周校军,嵇春艳,郑子波
(1.江苏科技大学 船舶与海洋工程学院,镇江 212003) (2.中交第一航务工程勘察设计院有限公司,天津 300222) (3.江苏科技大学 江苏省船舶先进设计制造技术重点实验室,镇江 212003) (4.大连理工大学 海岸和近海工程国家重点实验室,大连 116024) (5.河海大学 江苏省海岸海洋资源开发与环境安全重点实验室,南京 210098) (6.大连理工大学 船舶工程学院,大连 116024)
港湾共振是指当近岸海域的低频波浪传播到港湾内,如果其周期和港湾本征周期相一致,那么就会激起港湾内剧烈的水体共振的现象.港湾共振可以诱发港内泊船的剧烈运动,显著影响系泊安全和货物装卸[1].实际港口的本征周期大多在几分钟至1 h范围内.在自然界中,能够诱发显著的港湾共振的外力有多种.这些外力包括低频波浪、大气压力扰动、海啸波以及近岸滑坡或结构物坠落产生的冲击波等[2].然而,对于大部分港口,最常见的外力往往是从外海入射的波群.典型的风浪和涌浪总是以波群的形式向前传播,尽管它们的周期仅为几秒至十几秒,但由于波浪非线性,波群会产生二阶锁相长波,而这些长波往往会诱发港内长周期的水体共振现象[3].
文献[4]中通过对澳大利亚的Two Rocks港进行实地观测,证实了Two Rocks港内的水体共振现象是由伴随着入射波群传播的锁相长波导致的.他们还通过Boussinesq模型模拟发现:当外海波群向岸传播时,相对于外海低频波浪的能量,在近岸珊瑚礁系统上的低频波浪能量大约增大8~10倍,进而显著增大了Two Rocks港内水体发生长周期共振的风险[5].文献[6-7]中通过实验和数值模拟的方法也证实了近岸珊瑚礁地形能够显著增大低频波浪的能量.
文献[8]中提出了基于最小二乘法的分离港内低频波浪的方法,并基于此波浪分析技术,研究了在港湾发生第1共振模态条件下短波波长的变化对于港内锁相长波和自由长波波幅以及它们的相对成分的影响.随后,文献[9]中将此研究拓展到最低的4个共振模态,并进一步研究了入射短波波幅的变化对于它们的影响.然而,文献[8-9]中均将港外地形假设为平底,并未考虑近岸地形对于港湾长周期共振的影响.与此不同,文中不再假设港外地形为平底,而是将近岸珊瑚礁地形考虑在内.
文中将系统研究近岸珊瑚礁地形外坡坡度和形状变化对于港湾共振条件下港内自由长波、锁相长波以及它们相对成分的影响.受到文献[10]的启发,文中将使用斜坡地形、反正切型地形和双曲余弦型地形等不同形状地形作为近岸珊瑚礁外坡地形.文中的研究将对我国南海岛礁上的港口建设提供理论指导,以期能够降低这些港口发生港湾共振的风险.
1 数值模型和分析技术
1.1 数值模型
Boussinesq方程是近些年来被广泛地应用于模拟波浪在近岸的传播过程的一种数值模型.它可以精确地模拟波浪的色散性、非线性、浅水变形、破碎和波成流等一系列现象[11].文中采用FUNWAVE模型[12]来进行数值模型实验.该模型以文献[13]中提出的色散性精确到二阶的完全非线性Boussineq方程为基础开发.
采用笛卡尔坐标系,x和y轴位于静水面,z轴以垂直向上为正,则控制方程表达式为:
(1)
式中:
M= (h+η)u+(h+η)·


(2)
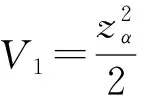
(3)
V2=[(zα-η)(uα·)(·(huα))+
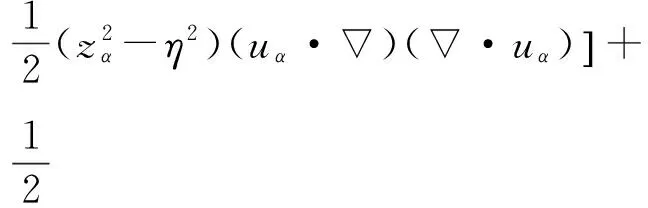
(4)
uα为zα=-0.531h时x和y方向的水质点速度,η为自由水面.对以上的控制方程采用文献[14]中提出的有限差分格式进行求解,对方程中空间的一阶和二阶导数分别采用五点和三点中心差分格式,边界附近的点采用相应的偏心差分格式.控制方程的时间离散则使用预估—校正法进行处理.预估步骤采用三阶显式Adams-Bashforth格式,校正步骤采用四阶隐式Adams-Moulton格式.为方便边界的处理,采用域内源造波与海绵层结合的方法.域内源造波采用文献[15]中提出的方法,即在计算域内设置造波区,产生向造波区一侧传播的波浪.海绵层即在固壁边界前设置1~2倍波长的人工阻尼区使波浪衰减.
文献[16]中采用FUNWAVE模型模拟了文献[17]中的物理实验,通过将模拟得到的港湾共振条件下1~3倍频波浪成分沿港内中轴线的分布与物理实验结果进行比较,发现它们之间吻合很好,表明该数值模型能够精确地模拟港湾共振现象.
1.2 分离方法
文中采用文献[8]中提出的港内低频波浪的分离程序来将港内的低频波浪成分进一步分解为低频锁相驻波和低频自由驻波成分.
图1呈现了港口平面和测点布置情况.港口长度L=50.0 m,宽度W=5.0 m.港池内的水深常数hI=1.0 m.沿着港口中轴线等间距地布置N=21个测点.相邻两个测点的间距D=2.5 m.测点G01布置在港口底墙处.海岸线和港内边墙均设置为全反射直墙.笛卡尔坐标系统(o,x,y,z)的原点取在静水面,z轴以垂直向上为正.

图1 实验布置和测点位置示意图Fig.1 Definition sketch of the experimental setupand the location of the wave gauges
在港外,由频率分别为f1和f2的自由短波组成的双色波群垂直于口门入射.根据文献[3]中对双色波垂直口门入射情况下狭长矩形港内波浪的公式描述,港内的低频波浪成分可以表示为:
ηL=ζbcos[(2πΔf)t-αb]cos(Δkx)+
ζfcos[(2πΔf)t-αf]cos(κx)
(5)
式中:
Δf=|f1-f2|
Δk=|k1-k2|
(2πf1)2=gk1tanh(k1hI)
(2πf2)2=gk2tanh(k2hI)
(2πΔf)2=gκtanh(κhI)
式(5)等号右端第1项为低频锁相驻波,第2项为低频自由驻波.ζb、ζf分别为低频锁相驻波和低频自由驻波的波幅.Δk、κ分别为低频锁相驻波和低频自由驻波的波数.αb、αf分别为低频锁相驻波和低频自由驻波的初始相位.k1和k2分别为港内短波f1和f2成分的波数.
对式(5)进行一系列的三角变换,可以得到港内低频波浪波幅沿着中轴线变化的解析表达式:
A(x)2=aφ0(x)+bφ1(x)+cφ2(x)
(6)
式中:
(7)

文献[8-9]中使用已知的解析信号对该低频波浪分离程序的精确性进行检验,证明了它能够在不同的共振模态条件下精确地将港内的低频波浪成分进一步分解为锁相长波和自由长波.
2 数值实验布置
使用针对狭长型矩形港口发生共振的线性解析解[18],可以计算出文中所用港口的放大因子曲线(图2).

图2 港口的放大因子曲线Fig.2 Amplification factor curve for the rectangle harbor
可见,图1所示港口的最低5个模态的共振频率分别为0.014、0.043、0.073、0.103和0.133 Hz.文中仅研究双色波群垂直于港口口门入射并诱发港内产生第1共振模态的情况.文中所有数值实验中,入射双色波群中的短波频率f1和f2均分别设置为0.250、0.264 Hz,则伴随波群传播的锁相长波的频率Δf=0.014 Hz,其与港口的第1模态的共振频率相一致,因此在双色波群的作用下港内将发生第1模态的水体共振[3].对于入射双色短波波幅,则考虑3种情况:①a1=a2=0.02 m;②a1=a2=0.05 m;③a1=0.05 m、a2=0.02 m.a1、a2分别为入射f1和f2短波成分的波幅.前两种情况下,入射双色波群为完全调制的,而对于第3种情况,波群为弱调制的.
图3为文中所用的数值波浪水池和港口内外地形布置示意图.数值波浪水池尺寸为1 257.8 m×2 084.2 m.港外的珊瑚礁礁坪的长度为50.0 m,礁坪处的水深与港内水深相同,均为hI=1.0 m.为了研究珊瑚礁外坡坡度对于港内低频波浪的影响,外坡设置为常坡度,在100.0 m≤x≤(100.0+b)m范围内,水深可解析表达为:
h(x)=hI+γ(x-100) (常坡度地形)
(8)
外坡宽度b在5.0~100.0 m之间变化.外海的水深常数h0=5.0 m,则外坡坡度γ在0.04~0.80的范围内变化.根据线性色散关系,频率Δf=0.014 Hz的低频自由长波在水深h0=5.0 m时的波长为499.9 m,为了充分吸收向外海辐射的低频长波,在数值波浪水池的右边界和上下边界分别布置了宽度分别为1 002.8 m和1 000.6 m的海绵层,均略大于低频自由长波波长的2倍.因为图1所示港口沿中轴线对称,为了节省计算网格和时间,仅模拟港口和外海的一半区域.港内等间距布置了N=21个测点.x方向网格尺寸Δx从港内至造波区均为0.5 m,而在海绵层内则从0.5 m逐渐增大到18.7 m;y方向网格尺寸Δy从港内的0.5 m逐渐增大至19.9 m.计算域中包含285 200个网格数和286 431个节点数.所有的实验中时间步长均取为0.025 s.数值模型模拟到2 000.0 s,总计80 000个时间步.
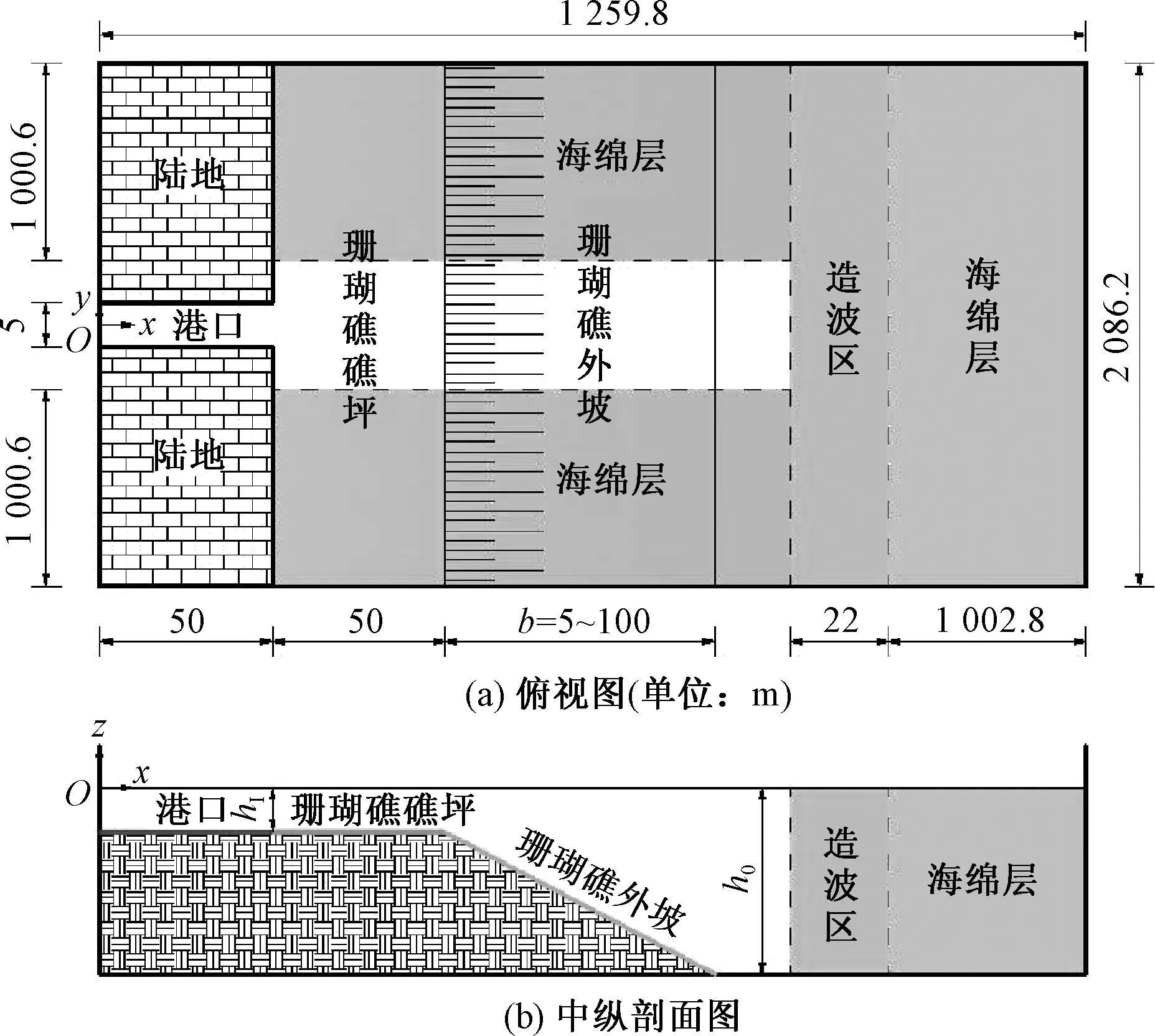
图3 数值波浪水池示意图Fig.3 Sketch of the numerical wave basin
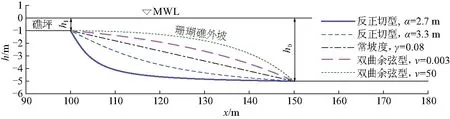
图4 当b=50.0 m时珊瑚礁外坡不同形状地形比较Fig.4 Comparison of various bottom shapes over the reef slope under the condition of b=50.0 m
为了研究珊瑚礁外坡形状对港内低频波浪的影响,在珊瑚礁外坡宽度b=50.0 m和100.0 m时,文中还考虑了反正切型地形和双曲余弦型地形,即在100.0 m≤x≤(100.0+b)m范围内,水深可解析表达为:
h(x)=hI+αatan[β(x-100)] (反正切型地形)
(9)
h(x)=hIcoshκ[μ(x-100)] (双曲余弦型地形)
(10)
几何参数α、β、ν和μ用于决定珊瑚礁外坡的形状,它们满足如下关系:
(11)
(12)

(13)


表1 珊瑚礁外坡形状参数Table 1 Geometric parameters of the reef slope inall the numerical experiments
3 结果和分析
3.1 珊瑚礁外坡坡度对于港内低频波浪的影响
当波群传播到港内时,水体将从初始的平静状态逐渐达到稳定状态.文中对于港内初始反应阶段的波况不予考虑,仅对达到稳定状态的港内波况进行研究[8-9].对各测点达到平稳的波面时间序列采用离散序列傅里叶级数展开的方法提取出差频成分的波幅,然后使用文中的波浪分离程序将差频成分进一步分解为锁相驻波和低频自由驻波成分.图5为当b=50.0 m时在珊瑚礁外坡形状分别为α=2.7 m的反正切型、常坡度型和ν=50的双曲余弦型条件下,由不同波幅双色波群入射产生的港内各测点实测的差频成分波幅和采用最小二乘法拟合得到波幅包络线.图中AL表示差频成分波幅,a=(a1a2)1/2为入射双色短波的平均波幅.可以看出,对于不同波幅的入射双色波和不同形状的珊瑚礁外坡,港内实测的数据点与拟合得到的曲线均吻合得很好,这表明使用文中的波浪分离方法计算得到港内低频自由长波和锁相长波的结果是精确可靠的.文中以a1=a2=0.02 m时的情况为例.当珊瑚礁外坡形状为α=2.7 m的反正切型时(图5(a)),分离得到的锁相驻波波幅ζb=4.61×10-3m,低频自由驻波波幅ζf=9.99×10-3m,相位差|αb-αf|=97.16°;当珊瑚礁外坡形状为常底坡型时(图5(b)),ζb=4.64×10-3m,ζf=9.12×10-3m,|αb-αf|=86.70°; 当珊瑚礁外坡形状为ν=50的双曲余弦型时(图5(c)),ζb=4.75×10-3m,ζf=9.02×10-3m,|αb-αf|=74.09°.文中用振幅比ζb/ζf来定量表示锁相驻波和低频自由驻波的相对成分.在以上3组实验中,振幅比分别为46.12%、50.75%和52.72%.

图5 当b=50.0 m时港内各测点实测的差频成分波幅(点)和使用最小二乘法拟合得到的波幅包络线Fig.5 Subharmonic component amplitudes (dot) in all gauges and their envelope line obtained by usingthe separation procedure under the condition of b=50.0 m
图6为当珊瑚礁外坡为常坡度地形时港内低频自由驻波波幅ζf和锁相驻波波幅ζb随着珊瑚礁外坡坡度系数(即坡度的倒数)的变化.由图可知,对于文中所考虑的3种入射波波幅,珊瑚礁外坡坡度的变化对于港内低频自由驻波成分的影响较大.具体来说,港内低频自由驻波的波幅随着珊瑚礁外坡坡度的增大而增大,而港内锁相驻波成分则对珊瑚礁外坡坡度的变化并不敏感.在文中所研究的外坡坡度变化范围内,港内锁相驻波波幅仅随着外坡坡度的增大略有减小.同时,由于低频自由长波在港内被共振放大,其波幅始终显著大于港内锁相长波的波幅,这与文献[8-9]中的发现相一致.图7为在不同入射波波幅条件下振幅比ζb/ζf随着外海珊瑚礁外坡坡度系数的变化.可以发现,无论入射双色短波波幅的大小以及双色波群是否为完全调制的,振幅比ζb/ζf均随着外坡坡度系数的减小(即珊瑚礁外坡坡度的增大)而减小.另外,还可以发现随着入射短波波幅的增大,振幅比ζb/ζf略有减小.对于入射波波幅a1=a2=0.02 m的情况,ζb/ζf在44.39%~55.29%;当a1=0.05 m、a2=0.02 m时,ζb/ζf则在38.25%~53.17%;当a1=a2=0.05 m时,ζb/ζf则在33.37%~48.52%.

图6 港内低频自由驻波和锁相驻波波幅随着珊瑚礁外坡坡度系数的变化Fig.6 Variations of amplitudes of bound and free longstanding waves with the slope coefficient of thereef slope
3.2 珊瑚礁外坡形状对于港内低频波浪的影响

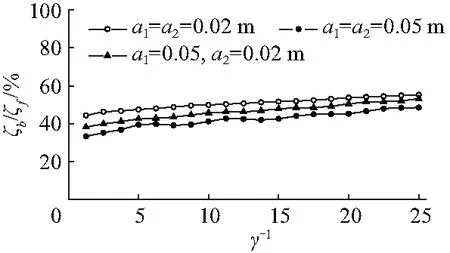
图7 振幅比ζb/ζf随着珊瑚礁外坡坡度系数的变化Fig.7 Variations of the amplitude ratios, ζb/ζf, with the slope coefficient of the reef slope
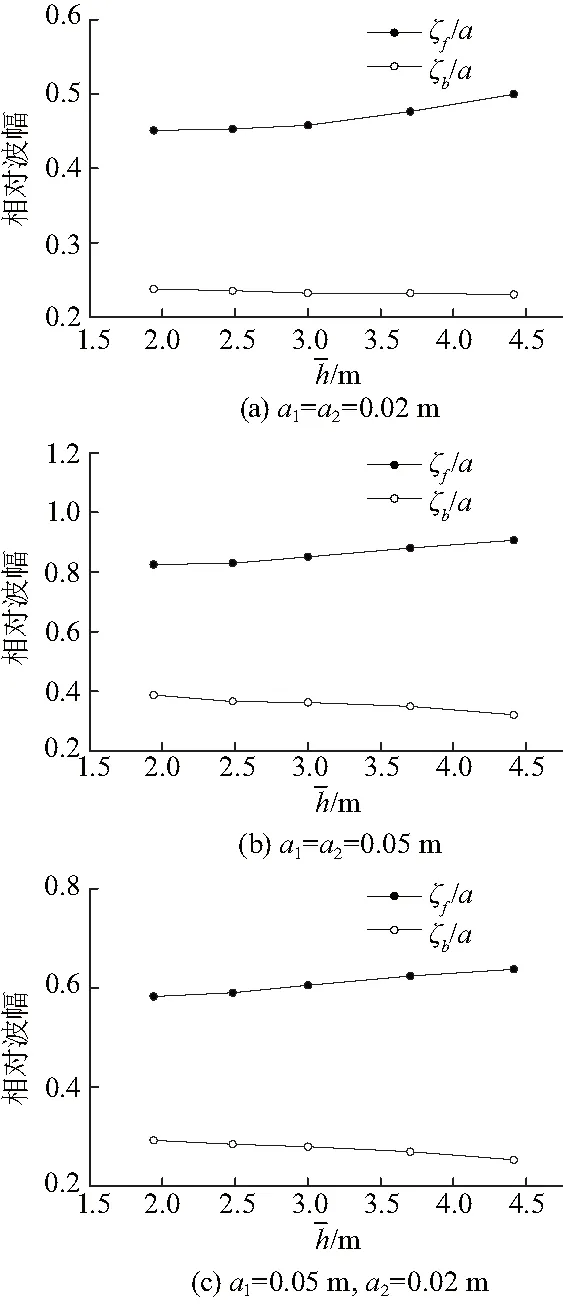
图8 当b=50.0 m时,港内低频自由驻波和锁相驻波波幅随着珊瑚礁外坡平均水深的变化Fig.8 Variations of amplitudes of bound and free longstanding waves with the mean water depth overthe reef slope, under the condition of b=50.0 m

图9 当b=50.0 m时,振幅比ζb/ζf随着珊瑚礁外坡平均水深的变化Fig.9 Variations of the amplitude ratios, ζb/ζf,withthe mean water depth over the reef under the condition of b=50.0 m


图10 当b=100.0 m时,港内低频自由驻波和锁相驻波波幅随着珊瑚礁外坡平均水深的变化Fig.10 Variations of amplitudes of bound and free longstanding waves with the mean water depth overthe reef under the condition of b= 100.0 m

图11 当b=100.0 m时,振幅比ζb/ζf随着珊瑚礁外坡平均水深的变化Fig.11 Variations of the amplitude ratios, ζb/ζf, with the mean water depth over the reef under the condition of b=100.0 m
4 结论
使用FUNWAVE模型模拟了由双色波群诱发的狭长矩形港内的二阶长波共振现象.文中考虑了近岸珊瑚礁地形对于港湾共振的影响.采用一个基于最小二乘法的分离港内低频波浪的方法,对港口发生第一共振模态时,港内锁相长波和自由长波成分及其它们的相对成分随着珊瑚礁外坡坡度和形状变化进行了系统研究,并得到以下结论:
(1) 对于文中所研究的特定港口和珊瑚礁外坡坡度的变化范围,港内自由长波的波幅随着珊瑚礁外坡坡度的增大而增大,而港内锁相驻波成分则对珊瑚礁外坡坡度的变化并不敏感.前者由于在港内被共振放大,其波幅始终要显著大于后者的波幅.振幅比ζb/ζf随着珊瑚礁外坡坡度的增大而减小.
(2) 珊瑚礁外坡形状对港内自由长波和锁相长波的影响有所不同.对于港内自由长波,珊瑚礁外坡形状对它的影响还与珊瑚礁外坡宽度有关.当b=50.0 m时,港内自由长波波幅随着珊瑚礁外坡平均水深的增大而增大;而当b=100.0 m时,港内自由长波波幅随着珊瑚礁外坡平均水深的增大出现了先减小后增大的变化趋势.对于港内锁相长波,当b=50.0、100.0 m时,它均随着珊瑚礁外坡平均水深的增大而逐渐减小.
以上结论仅针对文中所使用的特定港口、珊瑚礁外坡坡度和形状变化范围.
参考文献(References)
[ 2 ] RABINOVICH A B.Seiches and harbor oscillations[M].Handbook of Coastal and Ocean Engineering, 2009: 193-236.DOI:10.1142/9789812819307-0009.
[ 3 ] BOWERS E C. Harbour resonance due to set-down beneath wave groups[J]. Journal of Fluid Mechanics,1977,79:71-92.DOI:10.1017/s0022112077000044.
[ 4 ] THOTAGAMUWAGE D T, PATTIARATCHI C B. Observations of infragravity period oscillations in a small marina[J]. Ocean Engineering, 2014, 88: 435-445. DOI:10.1016/j.oceaneng.2014.07.003.
[ 5 ] THOTAGAMUWAGE D T, PATTIARATCHI C B. Influence of offshore topography on infragravity period oscillations in Two Rocks Marina, Western Australia[J]. Coastal Engineering, 2014, 91: 220-230. DOI:10.1016/j.coastaleng.2014.05.011.
[ 6 ] NWOGU O, DEMIRBILEK Z. Infragravity wave motions and runup over shallow fringing reefs[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2010, 136(6): 295-305. DOI:10.1061/(asce)ww.1943-5460.0000050.
[ 7 ] YAO Y, HUANG Z, MONISMITH S G, et al. 1DH Boussinesq modeling of wave transformation over fringing reefs[J]. Ocean Engineering, 2012, 47: 30-42. DOI:10.1016/j.oceaneng.2012.03.010.
[ 8 ] DONG G, GAO J, MA X, et al. Numerical study of low-frequency waves during harbor resonance[J]. Ocean Engineering, 2013, 68: 38-46. DOI:10.1016/j.oceaneng.2013.04.020.
[ 9 ] GAO J, JI C, GAIDAI O, et al. Numerical study of infragravity waves amplification during harbor resonance[J]. Ocean Engineering, 2016, 116: 90-100. DOI:10.1016/j.oceaneng.2016.02.032.
[10] GAO J, JI C, LIU Y,et al. Numerical study on transient harbor oscillations induced by solitrary waves[J]. Ocean Engineering,2016,126:467-480.
[11] KIRBY J T. Boussinesq models and applications to nearshore wave propagation, surf zone processes and wave-induced currents[J]. Elsevier Oceanography Series,2003,67(3):1-41.
[12] KIRBY J T, LONG W, SHI F. Funwave 2.0 fully nonlinear boussinesq wave model on curvilinear coordinates [R]. [S.l.]:University of Delaware, 2003.
[13] WEI G, KIRBY J T, GRILLI S T, et al. A fully nonlinear Boussinesq model for surface waves. I. highly nonlinear, unsteady waves[J]. Journal of Fluid Mechanics, 1995,294(294):71-92.
[14] WEI G, KIRBY J T. Time-dependent numerical code for extended boussinesq equations[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1995, 121(5): 251-261. DOI:10.1061/(asce)0733-950x(1995)121:5(251).
[15] CHAWLA A, KIRBY J T. A source function method for generation of waves on currents in Boussinesq models[J]. Applied Ocean Research, 2000, 22(2): 75-83. DOI:10.1016/s0141-1187(00)00005-5.
[16] DONG G, WANG G, MA X, et al. Numerical study of transient nonlinear harbor resonance[J]. Science China Technological Sciences, 2010, 53(2): 558-565. DOI:10.1007/s11431-009-0409-5.
[17] ROGERS S R, MEI C C. Nonlinear resonant excitation of a long and narrow bay[J]. Journal of Fluid Mechanics, 1978, 88(1): 161. DOI:10.1017/s0022112078002037.
[18] MEI C C. The applied dynamics of ocean surface waves[M]. New York:Wiley,1983.
