夹杂物尺寸对粉末高温合金低周疲劳寿命影响的机制

刘新灵，胡春燕，王天宇

(1.中国航发北京航空材料研究院，北京 100095；2.航空工业失效分析中心，北京 100095；3.航空材料检测与评价北京市重点实验室，北京 100095；4.材料检测与评价航空科技重点实验室，北京 100095)

0 引言

在采用粉末冶金工艺制备高温合金的过程中，不可避免地会引入缺陷。粉末高温合金中的缺陷主要包括气孔、原始颗粒边界(PPB)、夹杂物等，其中夹杂物是最主要的缺陷[1]。粉末高温合金中的夹杂物通常可分为两类，一类是外来非金属夹杂物，另一类是异金属其他金属夹杂物。这两类夹杂物都与材料制备过程密切相关。外来非金属夹杂物多为脆性的陶瓷夹杂物，主要是含有Al、Si、Ca、Mg、O等元素的氧化物或复合氧化物，它们来源于母合金熔炼及制粉过程。另一类塑性较好的异金属夹杂物中，Nb、Mo、W等元素含量较高，它们来源于制粉过程中粉体快速凝固时遗留下来的母合金中高熔点偏析物。粉末高温合金中夹杂物以脆性的陶瓷夹杂为主[2-4]。

大量研究已经证明，外来非金属夹杂物对粉末高温合金的力学性能有显著的影响，它们易成为裂纹源，大大降低粉末高温合金的低周疲劳性能[5-6]。有关夹杂物对疲劳性能的研究是从断口裂纹源处发现的夹杂物开始的。通过对大量低周疲劳断口裂纹源的观察，得到了有关夹杂物的许多基本信息，对夹杂物所进行的研究工作包括对夹杂物的鉴别、评价以及夹杂物对粉末高温合金性能的影响，特别是对低周疲劳性能(LCF) 的影响，还有如何减少夹杂物数量、减小夹杂物尺寸的措施，以及考虑夹杂物因素的粉末高温合金寿命预测方法等[7-10]。

夹杂物对粉末高温合金低周疲劳性能的影响是夹杂物在基体中力学效应的最终结果，这种影响规律是建立在多种因素综合作用下的，主要与夹杂物尺寸、位置和形状密切相关。缺陷尺寸对疲劳性能的影响，主要是通过对试样断口进行观察分析，将缺陷的尺寸、位置与试样的疲劳寿命进行统计分析，得到缺陷尺寸对寿命影响的大致规律[11-15]，它属于特定试验条件下的统计结果，缺乏从力学角度分析缺陷尺寸变化对寿命影响的机制研究。

为了探讨夹杂物在基体中的作用规律，首先从解析角度分析夹杂物与合金基体界面问题。考虑到解析分析无法应用在复杂边界条件下，用计算机模拟的方法分析夹杂物与基体完好连接和夹杂物上含有孔洞两种情况下对界面应力、应变分布的影响，探索夹杂物尺寸变化对合金疲劳寿命影响的机理。

1 试验方法

试验用材料为FGH95粉末高温合金，将基体材料看作弹塑性材料，其弹性模量为193 GPa。夹杂物为Al2O3夹杂物，看作是全弹性材料，其弹性模量为400 GPa。

基体材料在500 ℃下的循环应力-应变曲线见图1，其循环应力-应变关系式为

(1)

式中：E为基体的弹性模量，193 GPa；K为硬化系数，1 730 MPa；n为硬化指数，0.051。

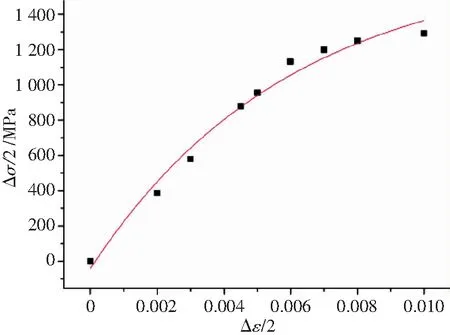
图1 合金基体材料循环应力-应变曲线(500 ℃,R=-1)Fig.1 Cyclic stress-strain curve of the basal body alloy

模拟方案：将二维平面的3个应力分量转换成极坐标系下的2个应力分量，将有限元软件在直角坐标系下的计算结果σx、σy和τxy转换成极坐标系下的应力分量σn、τt(图2)。建立图2所示微元的平衡方程：

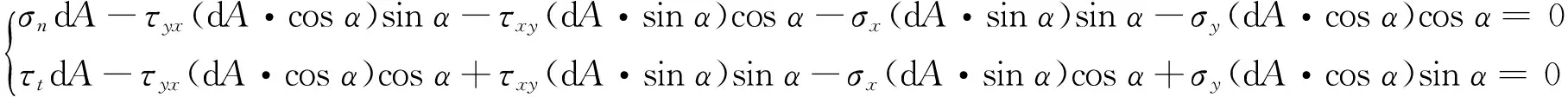
(2)

舍去dA，根据三角函数的平方公式得到：

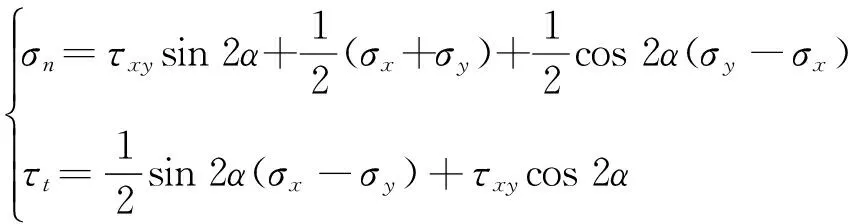
(3)

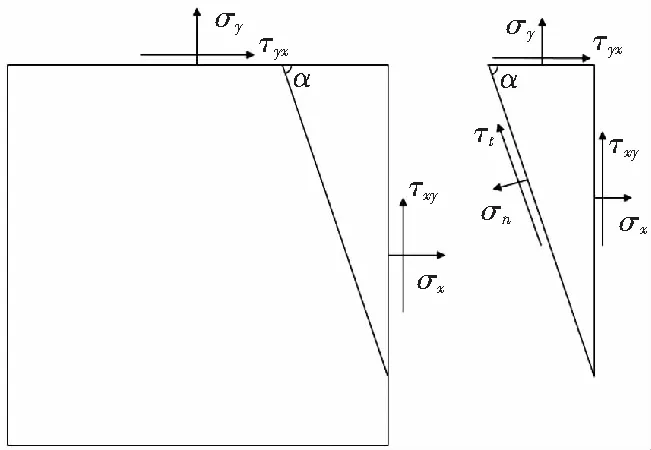
图2 局部坐标转换示意图Fig.2 Sketch of transformation of local coordinates

已经给出了无限大基体中圆形异质夹杂物的解析解，表明夹杂物界面应力在基体中的分布规律，但是此解析解无法计算有限边界基体条件和夹杂物位置的影响，因此需要进行有限元仿真。

2 界面应力分布模拟结果

将夹杂物设为圆形，通过改变夹杂物的大小，观察应力分布变化，分别考虑夹杂物在材料中心、表面和亚表面3种情况。利用ANSYS有限元进行模拟，ε=0.85%。

1)夹杂物在中心。

二维平板尺寸为10 mm×10 mm，在平板中心存在一个半径R的圆形夹杂物，根据粉末高温合金实际夹杂物尺寸范围，R分别取50、100、200 μm。其几何形式如图3a所示。有限元计算时，利用其对称性取1/4建立模型。为保证计算精度，选择使用ANSYS8节点二次平面单元PLANE82，网格划分为四边形结构网格。为控制计算规模并保证关键区域计算精度，采取在缺陷处局部加密，然后经过渡区到基体逐渐稀疏的方式划分网格。计算规模共157 849节点，52 288单元。缺陷局部网格划分情况如图3b所示。

图3 中心夹杂物示意图及模型网格划分Fig.3 Schematic diagram and grid partitioning of center inclusion

3种尺寸夹杂的界面径向应力和切应力按圆周角分布对比图见图4。当夹杂物位于内部时，不同夹杂物尺寸对应力分布的影响很小，基本保持不变。计算模型中夹杂与基体特征尺寸比例为1：50～1：200之间，在这一尺度范围内最大径向应力差别为2.1%，最大切应力差别小于1%，可以忽略不计。

2)夹杂物在表面。

二维平板尺寸为10 mm×10 mm，在平板左右表面各存在1个半径为R的半圆形夹杂物，R分别取50、100、200 μm。其几何形式如图5所示。有限元计算时利用其对称性使用1/4模型，单元与网格划分形式同夹杂在中心的情况。

3种尺寸夹杂的界面径向应力和切应力按圆周角分布对比见图6。可知，当夹杂物位于材料表面时，不同夹杂物尺寸对应力分布的影响同样很小。计算模型中夹杂与基体特征尺寸比例为1：50～1：200，在这一尺度范围内界面最大径向应力差别为0.8%，最大切应力差别为0.6%，可以忽略不计。

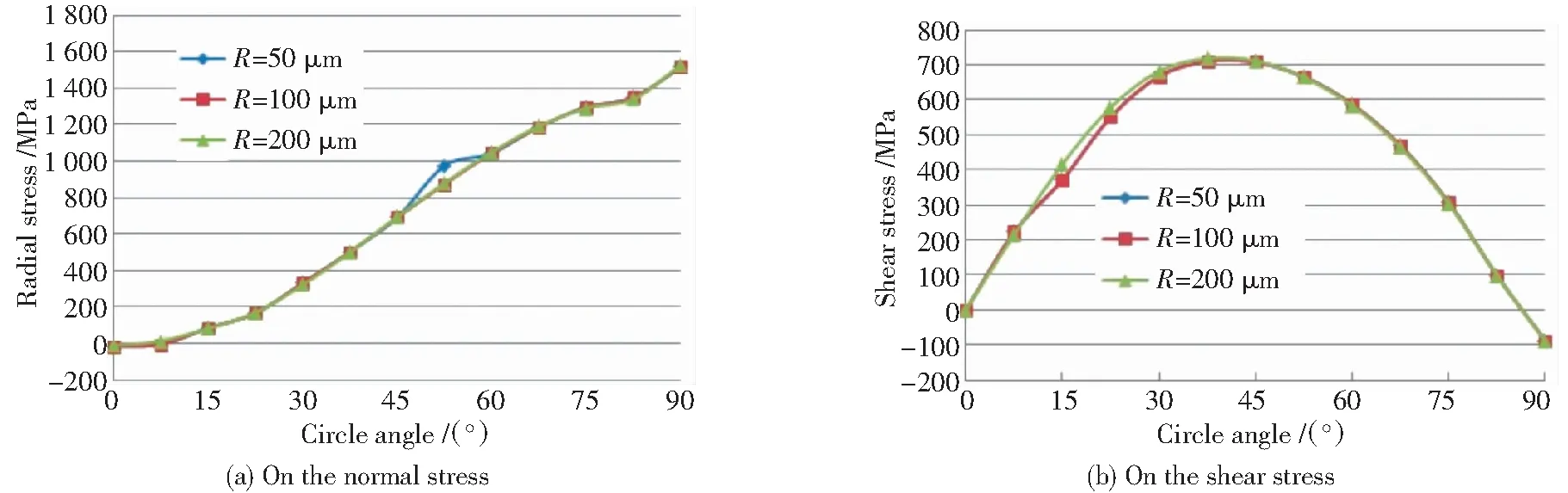
图4 不同尺寸的中心夹杂物对界面应力分布的影响Fig.4 Influence of center inclusion size on the stress distribution of the interface

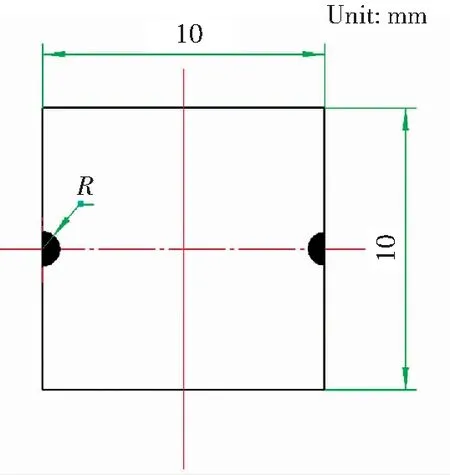
图5 夹杂位于表面的示意图Fig.5 Schematic diagram of surface inclusion

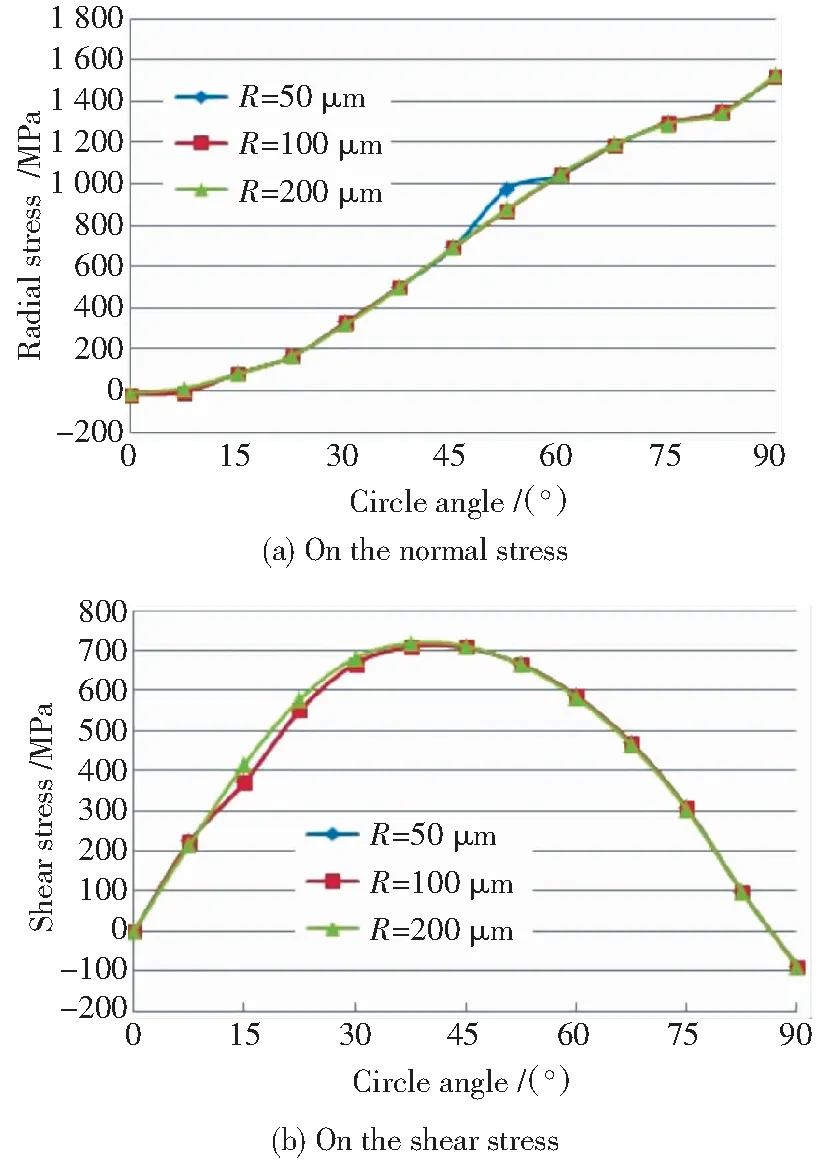
图6 不同尺寸的表面夹杂物对界面应力分布的影响Fig.6 Influence of surface inclusion size on the stress distribution of the interface

3)夹杂物在亚表面。

二维平板尺寸为10 mm×10 mm，在平板左边界0.1 mm深度处存在一个半径为R的圆形夹杂物，R分别取50、100、200 μm。其几何形式如图7a所示。有限元计算时利用其对称性使用1/2模型。同样，选择使用8节点二次平面单元PLANE82，网格划分为四边形结构网格。类似地，采用分区控制网格密度方式划分。计算规模共80 609节点，26 624单元。缺陷局部网格划分情况如图7b所示。

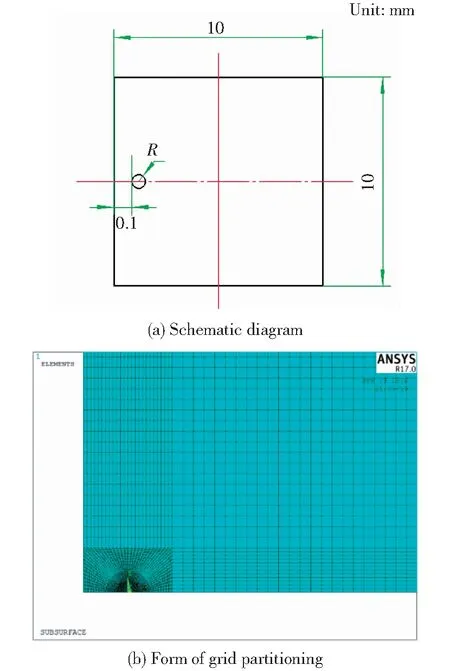
图7 中心夹杂物示意图及模型网格划分Fig.7 Schematic diagram and grid partitioning of subsurface inclusion

3种尺寸夹杂的界面径向应力和切应力按圆周角分布对比见图8。可知，当夹杂物位于材料亚表面时，不同夹杂物尺寸对应力分布的影响同样很小。计算模型中夹杂与基体特征尺寸比例为1：50～1：200之间，在这一尺度范围内界面最大径向应力差别为1.2%，最大切应力差别为1.1%，可以忽略不计。

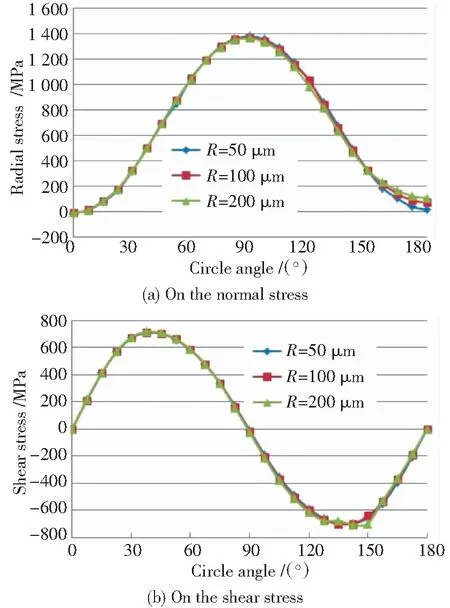
图8 不同尺寸的亚表面夹杂物对界面应力分布的影响Fig.8 Influence of subsurface inclusion size on the stress distribution of the interface

3 分析与讨论

从以上结果可以发现，对于界面完好连接的圆形夹杂物，无论夹杂物处在材料内部、表面还是亚表面，其几何尺寸大小对界面应力分布的影响都非常微小，其中最大应力的差别都小于2%，可以忽略不计。出现这种现象的根本原因是夹杂物特征尺寸与基体材料的特征尺寸相差很大，达到了1：50以上。这样在力学原理上，相当于无限大板带的夹杂问题，夹杂物尺寸在一定范围内变化时并不影响基体对于夹杂的尺寸优势。因此，无论夹杂物半径取50、100、200 μm，都不影响力学问题的本质。

然而，也可以发现，夹杂物位于亚表面时最大应力差别较其他两种情况相差较大。这是因为侧面边界对于夹杂物承载的影响，在改变夹杂物尺寸时，并没有改变它与表面的距离，导致模型没有等比例变化，造成应力分布的微弱变化；但夹杂物尺寸在实际范围内变化时，应力变化并不敏感。

可以发现，随着夹杂尺寸增大，界面正应力和切应力皆呈微小减小趋势，这种微小变化是由每个圆周角界面上点到有限边界条件的距离变化造成的。为了能够更为详尽反映夹杂物尺寸对界面应力的影响，定义夹杂物半径R与平板半长a的尺寸比例，其中a=5 mm。并继续进行更多尺寸比例的计算，且只取圆周角θ为90°的点的正应力σrr进行分析，变化趋势见图9， 图中直接以应力集中系数Kt表示。

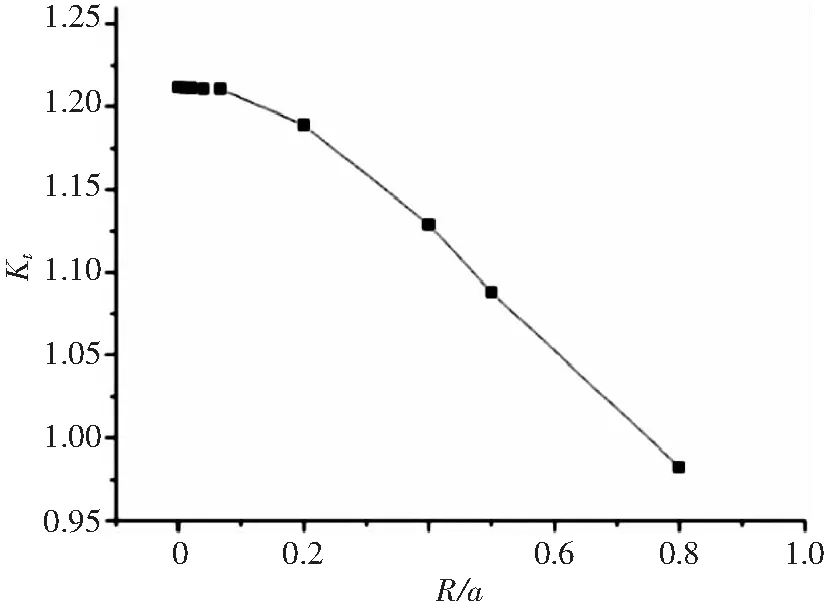
图9 圆周角θ为90°不同夹杂尺寸比例下σrr分量的应力集中系数Fig.9 Stress concentration factor of different inclusion size proportion(R/a) at the 90° angle for center inclusion

一般来说，夹杂物与基体材料的尺寸比例从实验室尺度到工程尺度约在1：50～1：10 000之间，图9显示了在这一尺度范围内，夹杂物尺寸对界面应力分布的影响时候非常微小的，几乎可以忽略不计。

实际上，夹杂物尺寸对结构的疲劳寿命有一定影响，对FGH99粉末高温合金在650 ℃、应变范围Δεt=0.82%，应变比R=0.05下进行低周疲劳试验，并对试验断口源区进行分析，统计源区存在缺陷的情况，包括源区缺陷形貌、缺陷尺寸和位置等(图10)。分析缺陷位于内部时对试样疲劳寿命的影响(图11)，可见，随着缺陷面积的增加，疲劳寿命呈幂函数下降。

缺陷尺寸对寿命影响的原因：异质夹杂物由于与基体材料物理上的不兼容性，容易在材料生产过程中出现不连续界面；夹杂物尺寸越大，它与

图10 FGH99粉末高温合金棒形试样源区夹杂物的形貌Fig.10 Morphology of inclusions in the source area of FGH99 powder superalloy bar

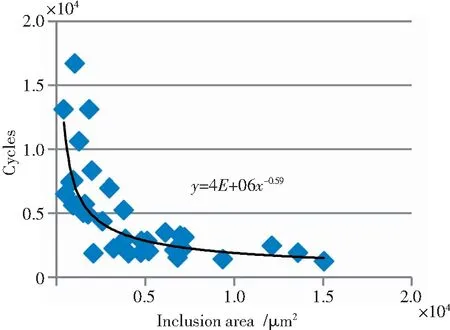
图11 缺陷位于内部情况下缺陷面积对寿命的影响Fig.11 Influence of internal inclusion area on fatigue life

基体的连接界面越大，则在界面上产生局部不连续的可能性就越大。相对于基体材料的连续性，这种不连续界面在力学模型中可以将其简化为初始裂纹或微孔。下面分析夹杂物/基体界面存在微孔缺陷时的尺寸效应。

二维平板宽10 mm，长10 mm，平板中心存在一个圆形硬夹杂物Al2O3。夹杂物圆心到试样表面的距离为5 mm，夹杂物尺寸分别取R=50、100、200 μm，在夹杂物圆周角θ=45°处存在一个孔洞，孔洞半径随着夹杂物尺寸变大也以相同比例变大。

同一位置夹杂物，在含有界面微孔洞情况时不同夹杂物尺寸仿真计算结果见图12，从图中可分析界面正应力和界面切应力随着圆周角呈不同的变化趋势。

可以看出，对于界面正应力，在圆周角0°～90°范围内均随着夹杂物尺寸增大而增大，且在θ=42.5°、47.5°和90°时增幅明显；对于界面切应力，在圆周角0°～30°和60°～90°范围内基本相当，在靠近圆周角42.5°和圆周角47.5°时随着夹杂物尺寸增大而微弱减小。

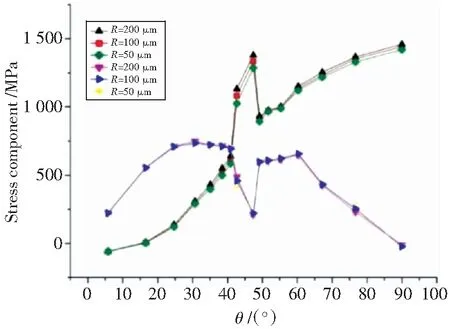
图12 界面存在微孔缺陷时的尺寸效应Fig.12 Inclusion size effect of the microporous defect in the interface

造成这一规律变化的主要原因是，夹杂物和基体在圆周角42.5°和圆周角47.5°形成非奇异界面端，使得该处的应力集中增大，自由表面处σrθ=0、σθ=0的边界条件使得界面正应力和界面切应力呈相反规律。

4 结论

1)研究了同一位置下，不同夹杂物尺寸对应力应变分布的影响，计算结果表明：当夹杂物/基体界面完好连接、不含微孔洞时，夹杂物与基体尺寸比例在实验室尺度(1：25)到工程尺度(1：10 000)范围内，夹杂物尺寸对应力应变影响很小，尺寸的改变，对最大径向应力与最大切向应力的影响一般不超过2%。

2)当夹杂物界面上含有微孔洞时，随着夹杂

物尺寸变大，界面正应力明显增大，界面切应力微弱减小，基体最大正应力和最大塑性应变均明显增大。夹杂物尺寸对疲劳寿命的影响，很可能是夹杂与集体的边缘并非完好连接，常常在界面处存在初始损伤破坏导致的。

参考文献

[1] 刘新灵,陶春虎. FGH96粉末高温合金损伤行为与寿命预测[J]. 失效分析与预防,2011,6(2):124-129.

[2] 张义文,上官永恒. 粉末高温合金的研究与发展[J]. 粉末冶金工业,2004,14(6):30-43.

[3] 邹金文,汪武祥. 粉末高温合金研究进展与应用[J]. 航空材料学报,2006,26(3):244-250.

[4] 国为民,吴剑涛,张凤戈,等. FGH95镍基高温合金粉末中的夹杂及其对合金疲劳性能的影响[J]. 粉末冶金工业,2000,10(3):23-28.

[5] 何承群,余泉茂,胡本芙. FGH95合金LCF断裂寿命与夹杂特征关系的研究[J]. 金属学报,2001,37(3):247-252.

[6] 张丽娜,张麦仓,李晓,等. 粉末高温合金中非金属夹杂物问题的研究进展[J]. 兵器材料科学与工程,2001,24(3):64-68.

[7] 国为民,冯涤,吴剑涛,等. 镍基粉末高温合金冶金工艺的研究与发展[J]. 材料工程,2002(3):44-48.

[8] Lautridou J C. Effect of inclusions on LCF life of PM superalloys for tuerboengine discs[C]. Conference: High Temperature Materials for Powder Engineer,1990(II):1163.

[9] Huron E S，Roth P G. The influence of inclusion on low cycle fatigue life in a P/M nickel-base disk superalloy[J]. Superalloys,1996:359-368.

[10] 邹金文,汪武祥. 粉末高温合金中夹杂物特性及其质量控制[J]. 粉末冶金技术,2001,19(1):7-11.