巧用“数学计算模型”计算20以内退位减法

新疆生产建设兵团第三师图木舒克市49团第一中学 赵 烨

笔者从教二十多年，一直以来都是教高年级数学，今年是第一次教一年级。在教学数数以及十以内加减法的内容时，学生都能轻松愉快地学习并掌握这些知识，可是对于20以内退位减法内容的学习、师生都下了很大功夫、收效还是不尽如人意。我又去问那些曾经教过一年级数学的老师，他们也说教学这块内容时，确实下了很大力气，但都没收到满意的效果。在计算20以内退位减法时，理论上学生都能背得烂熟（当个位不够减时，从十位退一、在个位上加十再减）。可是在实践运用时，学生每做一道题都要把退位减法的计算法则背一遍，这样学生做得又慢，错误率又高。但笔者在课堂上发现，一年级的孩子，喜欢获得直观性知识经验。于是积极引导学生去进行抽象、概括，建立数学模型，探求问题解决的方法，使学生进一步体验数学建模思想与方法。教学中，笔者始终坚持以学生发展为本的新理念，依据教材内容和学生的年龄特征，在课堂教学中和学生一起大胆实践、探索，通过观察、实验、分析等活动，终于发现并建立了20以内退位减法的计算模型，培养了学生解决问题的能力，增强学生的探究能力和创新意识。由原来学生厌烦的枯燥的理论说教转变成学生喜闻乐见的直观计算模型，孩子们利用自己发现并建立的计算模型很快学会了20以内退位减法的计算。现把我们的发现与大家一起分享，希望这一“模型计算法”能给曾经为学习退位减法的计算而犯难的师生们提供一种新的思想，一种新的方法。

数学“模型”计算法，它的算理仍旧是“破十法”。比如13-9，因为13是由一个10和一个3组成的，可以先用10减9，剩下的1和个位上的3合在一起就是4，所以13-9=4，但这是纯理论的东西，学生不容易理解也不喜欢接受。我们通过观察、实验、分析等活动，建立了20以内退位减法的计算模型、就能把这种理论变成直观的模型，学生看得懂，就学得会了。

首先以十几减9为例吧：在计算十几减9时，当个位不够减时，首先从十位退1（即10），用10-9=1，把这个1加在被减数的个位上，就是得数。请看下面十几减9的计算模型：

在计算十几减8时，算理同十几减9，当个位不够减时，先从十位退1（即10），用10-8=2，这个2加在被减数的个位上，就是得数。计算十几减8的模型：

同样的道理计算十几减7时，当个位不够减时，先从十位退一（即10），用10-7=3，这个3加在被减数的个位上，就是得数，计算十几减7的计算模型：

同样的道理建立以十几减6的计算模型：

再比如下面的十几减5的模型：

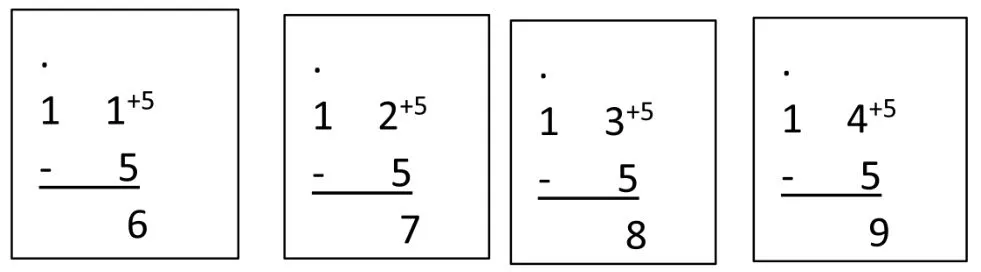
同理，利用“破十法”的减法算理还可以建立十几减4的计算模型、十几减3的计算模型……只要是20以内退位减都可以应运这种模型来进行计算。学生都能通过观察这个算式模型迅速而又准确地算出得数。这种计算方法不但适用于20以内退位减法，也可以推广到其他数位的退位减法上，只要能把这种计算方法掌握，就能大大提高同学们的计算速度和正确率。

数学建模思想是一种新的教学思想和教学手段，通过建模，把无形的抽象的理论转化成一种有“型”的“模子”。让学生在观察中发现、在观察中感悟、在观察中得出结论，既激发了学生的学习兴趣，又培养了学生爱动脑，爱思考，爱观察，爱发现的好习惯，同时也培养了学生解决问题的能力。

我们师生在学习实践中发现并建立的20以内退位减法计算模型给我们的教学和学习带来很大帮助，希望我们的这种模型计算法能得以推广，使更多师生掌握并应用。