空间摆动RCCC机构动力学分析

侍威， 赵国平， 王春明， 王华坤

（北京精密机电控制设备研究所研发中心，北京 100076）

0 引言

RCCC机构[1-8]作空间运动的基本构型，能够实现给定空间位置输出，与自由度的机器人机构相比，具有稳定性好、可靠性高、节省成本等优势，成为研究的重点方向。目前国内外学者主要针对RCCC机构位姿、运动精度与可靠性等方向[9-15]开展研究，基本没有开展RCCC机构构型与特性研究。

本文将RCCC空间机构进行演化，实现转动到摆动运动转换，提出空间摆动RCCC机构，为伺服电动舵机提供满足空间输出需求的新机构，在此基础上，针对空间摆动RCCC机构开展动力学分析，找出空间摆动RCCC机构各构件受力特点，为空间摆动机构的优化设计奠定了基础。

1 空间摆动RCCC机构演化

将典型的RCCC机构（如图1）进行参数设置（令h1=h2=h3=h0=0，s1=s2=s3=s0=0，轴间夹角α12=α23=α30=90°，α01为预设值，20°），推导出空间摆动RCCC机构（如图2），该机构可实现摆杆输出与旋转输出两种输出形式，满足多构型输出的需求。

图1 典型的RCCC机构

2 空间摆动RCCC机构动力学分析

图2 空间摆动RCCC机构构型图

图3 空间摆动RCCC机构运动分析坐标系

建立空间摆动RCCC机构运动分析坐标系如图3所示，图3中摆杆1绕Z轴旋转，作为输出,曲柄4作为输入。O-xyz是原点为O的固定坐标系。O-x″y″z″为连杆（叉子）的固连坐标系。O-x′y′z′的z′与z重合，x′与x″重合。图3（a）表示摆杆1处于中间位置，图3（b）表示曲柄4转过α角及摆杆摆过β角的位置姿态。

空间摆动RCCC机构中摆杆1和销轴2为定轴转动，连杆3为定点运动，曲柄4为定轴转动。现假设曲柄为匀速定轴转动。

1）将摆杆和销看做一个示力体，其受力情况如图4所示。

图4 摆杆和销轴受力图

列出动力学方程如下：

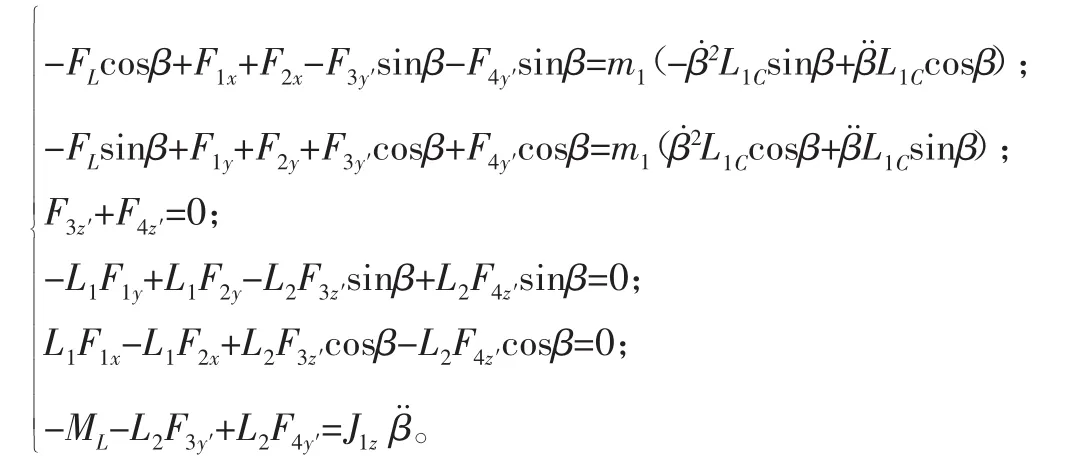
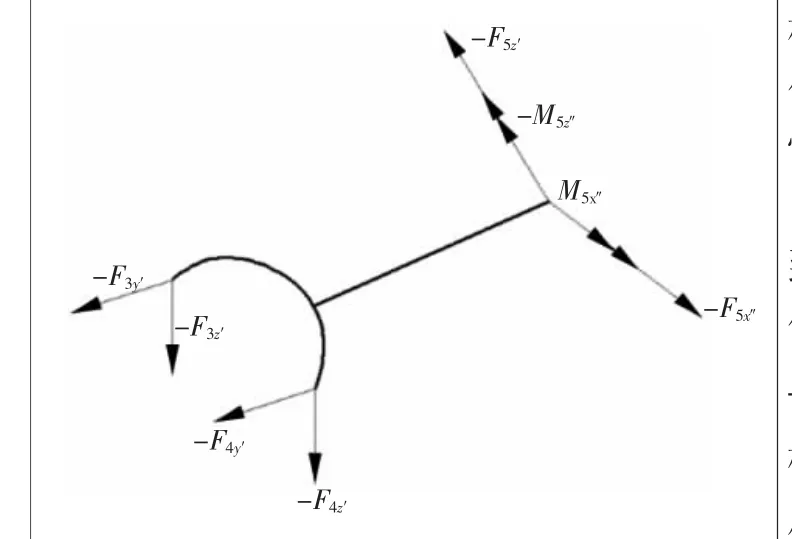
图5 连杆受力图

2）将连杆作为示力体，其受力情况如图5。

连杆受到销对它的作用力－F3、－F4，以及曲柄对它的作用力F5和力矩M5。－F3、－F4和这两个力对O之矩在O-x′y′z′中表示为：

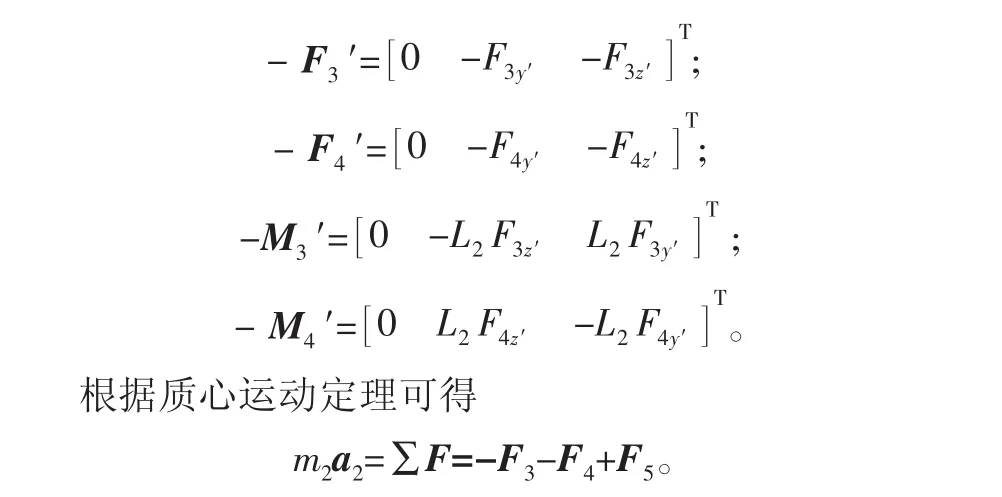
由于O-x″y″z″是连杆的惯量主轴系，所以根据刚体绕定点转动欧拉动力学方程可得：

其中，A、B、C分别指连杆对x″、y″、z″的转动惯量。

从O-x′y′z′到连杆固连坐标系O-x″y″z″与固定坐标系O-xyz的坐标变换矩阵分别为：

设连杆质心到O的距离为L2C，则连杆质心可以表示为

3）把曲柄作为受力体，其受力情况如图6。

图6 曲柄受力图

曲柄质心加速度为

其中L3C为曲柄质心到回转轴线的距离。建立曲柄的动力学方程组如下：

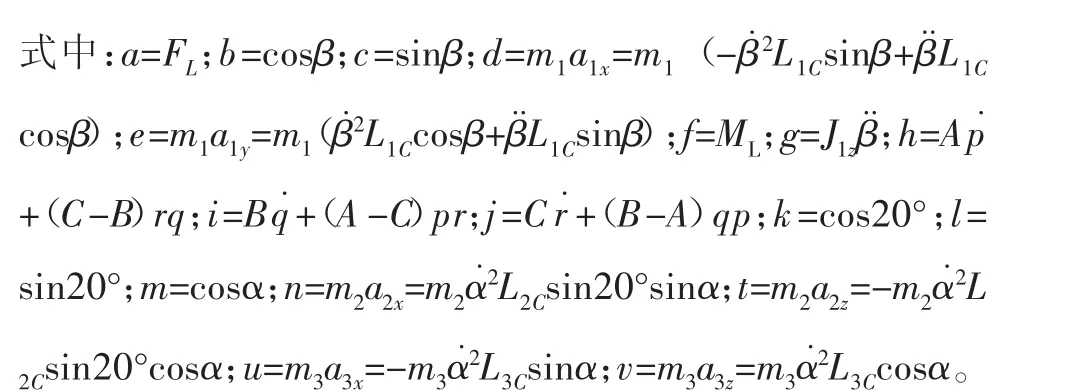
3 实例分析

设曲柄转速为75 r/min匀速输入，求得α˙=2.5πrad/s，L1=0.024 m，L2=0.017 m，L3=0.034 m，m1=1.1836 kg，m2=0.18926 kg，m3=0.52426 kg，J1z=2.3803×10－2kg·m2，ML=500 N·m，FL=500/0.3=1666.7 N，A=1.1056×10－4kg·m2，B=3.8229×10－5kg·m2C=1.2729×10－4kg·m2。将数据代入方程组，求得各处的反力与反力矩如图7～图14所示。

由图可见，销轴受连杆的作用力较大，峰值力达到15 600 N，且两端支撑受力一致；曲柄对连杆作用力比较小，峰值低于0.073 N，波动幅值低于0.01 N，曲柄对连杆的转矩相对较大，峰值达到532 N·m，波动幅值为33 N·m；壳体对曲柄的作用力最小，峰值低于0.0252 N，但对其转矩值达到501.35 N·m，其波动周期为其他受力周期的2倍。

4 结论

图7 摆杆受壳体的力F1-t变化曲

1）基于典型RCCC机构进行演化，得到紧凑型舵机用空间摆动RCCC机构，可实现摆动输出、旋转输出两种输出形式。2）通过空间摆动RCCC机构动力学分析，得出机构各构件之间的相互作用力大小与趋势，从而为空间摆动RCCC机构的结构设计提供理论依据。

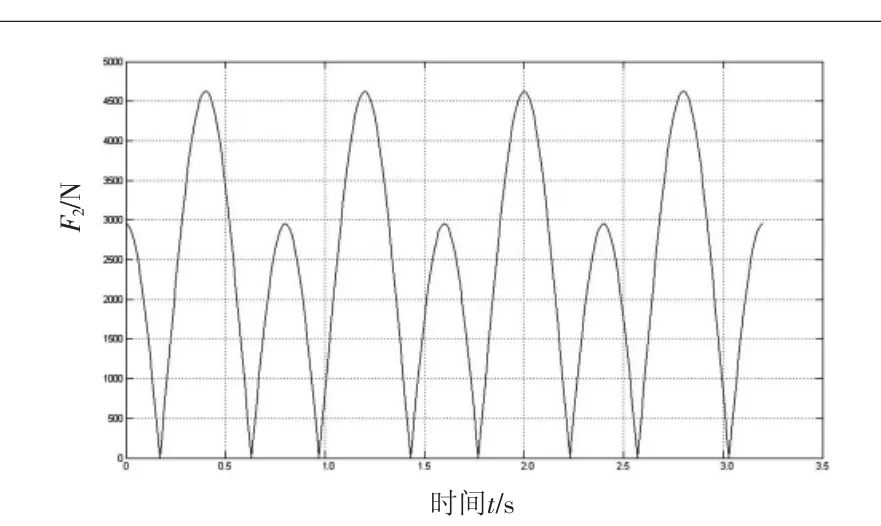
图8 摆杆受壳体的力F2-t变化曲线

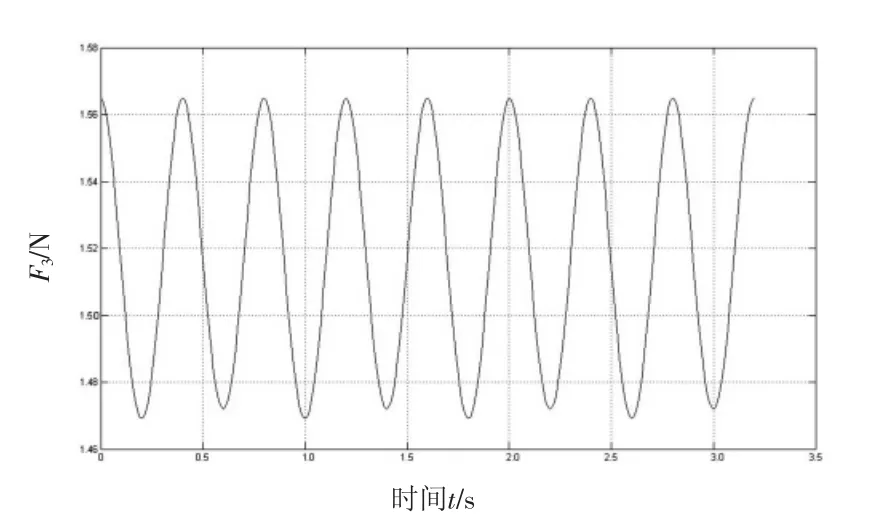
图9 销轴受连杆的力F3-t变化曲线

图10 销轴受连杆的力F4-t变化曲线

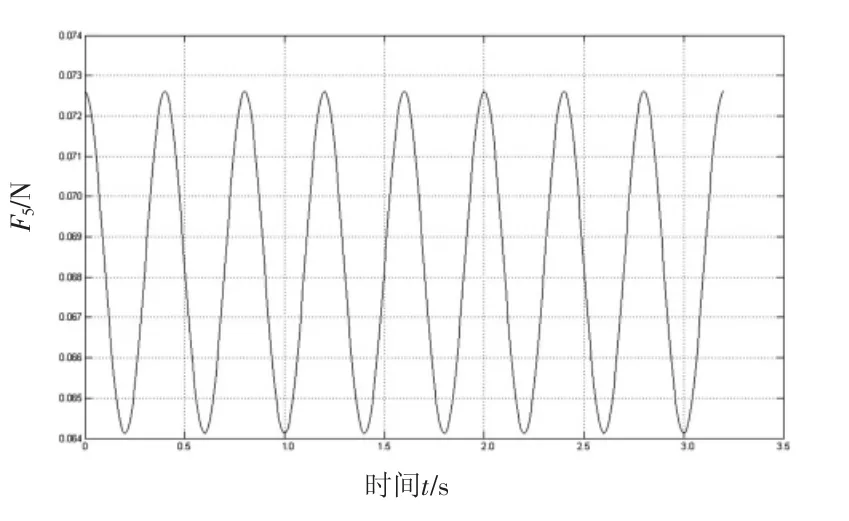
图11 曲柄对连杆的力F5-t变化曲线

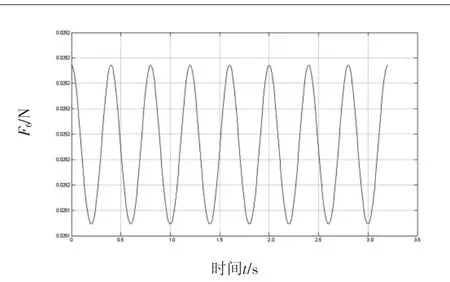
图12 壳体对曲柄的力F6-t变化曲线

图13 曲柄对连杆的力矩M5-t变化曲线

图14 壳体对曲柄的力矩M6-t变化曲线

[参考文献]

[1] 奥博连斯基,叶尔马科夫,苏霍鲁科夫.航空舵机系统设计理论[M].北京.航空工业出版社,2013.

[2] 张佑忠.简化快速电动舵机方案[J]航天控制,1985(1):48-53.

[3] 沈引中.大功率机电舵机设计研究[D].南京:南京航空航天大学,2012.

[4] 余波.飞行器舵机传动机构设计与性能分析[D].重庆:重庆大学,2014.

[5] 陆红.飞行器电动舵机系统的设计与实现[D].哈尔滨:哈尔滨工程大学,2012.

[6] 从强.空间机构技术发展趋势及展望[J].载人航天,2016(22):1-8.

[7] 杨维垣.空间机构分类及可靠性研究[J].航天器工程,1994(3):31-39.

[8] 王文魁.空间机构运动行为模拟概念研究[J].载人航天,2013(19):59-66.

[9] 褚金奎，孙建伟.RCCC机构轨迹综合的数值图谱法[J].中国机械工程,2009(20):1024-1028.

[10] 孙建伟，路贺，褚金奎.基于傅里叶级数的RCCC机构运动综合[J].中国机械工程,2014(21):2841-2847.

[11] 刘平，陈思专，张佩文.空间RCCC机构三维位形动态模拟[J].机械设计,2005(8):60-62.

[12] 史天录,邓洪洲,冯元生.RCCC空间机构的运动精度和可靠性分析[J].机械科学与技术,1995(1):47-51.

[13]黄胜兴.用线性方程组作空间机构的速度和加速度分析[J].武汉工学院学报,1998(2):53-67.

[14] 曹阳.基于解域的四位置空间RCCC机构综合[J].农业机械学报,2016(8):399-405.

[15] 孙建伟.利用数值图谱法进行RCCC机构的函数综合[J].中国机械工程,2008(6):713-717.