采用俞茂宏统一强度理论求解套管的极限外压强

田红亮, 何孔德, 陈从平, 钟先友, 郤能

(三峡大学机械与动力学院, 443002, 湖北宜昌)

强度理论用于判断材料在复杂应力下是否遭受破坏。对于各向同性材料,强度理论可以表述为3个主应力的标量函数。某种强度理论是否成立,在什么条件下能够成立,需要经受科学试验和生产实践的检验。1961年,西安交通大学的俞茂宏教授提出了双剪应力屈服准则[1]和十二面体广义双剪应力强度理论[2];1985年,他在双剪屈服准则的基础上引入拉压强度比α,提出了考虑拉压强度差和静水应力效应的广义双剪应力强度理论[3-4];1991年,他又在广义双剪强度理论的基础上引入中间主应力系数b,提出了静水应力型广义双剪应力屈服准则[5],从而创建了统一强度理论。俞茂宏统一强度理论的发展过程前后历经了30年。令人感兴趣的是,虽然各个阶段从不同的数学建模方程出发,但是得出的数学方程十分相似,这些十分简洁的表达式反映了它们之间的内在联系:双剪屈服准则是广义双剪强度理论在α=1时的特例,并且也是统一强度理论在b=1和α=1时的特例,而广义双剪强度理论则是统一强度理论在b=1时的特例。2002年,俞茂宏教授在著名的力学期刊《Applied Mechanics Reviews》上独撰发表了关于材料强度理论进展的论文[6],篇幅达50页之多。俞茂宏统一强度理论在强度理论的发展史上具有突出的贡献,得到了国内外同行的高度评价。

本文基于俞茂宏统一强度理论,研究油气井用套管的极限外压强。油气井的深度一般大于1 km,为保证安全生产及延长套管使用寿命,套管与地层间的空隙一般用水泥填充,套管、水泥以及地层三者间要紧密胶结。在油气田开发过程中,苛刻的工况往往会使套管腐蚀加剧,从而给生产安全带来隐患,可能造成生命财产损失和环境污染等问题[7]。受腐蚀及外压力的相互作用,套管的服役安全面临着严峻的挑战,尤其对高温高产油气井,套管还面临着高温高压的作用。多年以来,科技人员在试验和理论上对套管的极限压力进行了许多研究。例如:张微敬等为研究纵筋套筒挤压连接的预制柱抗震性能,给出了偏心受压承载力的计算表达式[8];杨睿月等采用蒙特卡罗方法预测了岩屑颗粒进入割缝筛管与连接油管之间环空的情况,并计算了环空中被岩屑颗粒堵塞的临界参数[9];刘波等对TBM斜井围岩应力场和渗流场进行耦合分析,基于统一强度理论对斜井围岩进行弹塑性力学研究,考虑中间主应力、侧压力系数、斜井倾角和渗流作用的影响,推导出了TBM斜井衬砌和围岩中应力、位移的解析表达式和塑性区半径计算公式[10];朱瑞林等在分析热应力与总应力特性的基础上,得出了最佳设计条件,提出了基于第四强度理论的热预应力自增强厚壁圆筒设计方法[11];陈梁等基于德鲁克-普拉格屈服准则和非关联流动法则,考虑中间主应力、塑性区弹性应变及岩体剪胀性的影响,推导了深部圆形巷道围岩应力、变形及塑性区半径的封闭解析解[12];Fang等计算了多层胶接套管的挤毁阻力[13];Deng等计算了套管的挤毁强度[14];刘奎等建立了套管在局部载荷作用下的应力计算模型,讨论了局部载荷范围、套管壁厚、套管外径对现场使用的P110套管受力与变形的影响[15];李宁波等为研究部分竖向分布钢筋套筒挤压连接的预制剪力墙的抗震性能,完成了3个预制墙试件和1个现浇墙试件的拟静力试验[16];齐昌广等考虑到路堤柔性荷载下刚性桩复合地基桩土存在沉降差,采用明德林应力解计算了塑料套管桩群在复合地基中产生的附加应力[17];曹雪叶等将冻结壁等效为弹性模量、黏聚力呈抛物线分布的功能梯度材料厚壁圆筒,基于统一强度理论并考虑中间主应力的影响,推导出了冻结壁的弹性极限荷载、弹塑性应力场及塑性极限荷载的解析解[18];Yin等预测了页岩气水平井中套管的压强[19];Huang等基于精细减缩模量计算方法,研究了套管挤毁的临界外压强[20];Xu等推导了地下圆孔围岩的统一强度理论解[21];Chen等基于大变形的弹塑性理论,提出了预测套管爆破压强的三维有限元模型[22];Zhang等考虑了弹性参数的匹配,用有限元方法获得了套管外压强的分布规律和影响[23]。

分析以上文献中套管极限压强的研究成果,发现存在4个方面的不足:①对理论模型方面的研究尚不多见,现有文献直接给出的公式大多缺乏实用性,理论上的原创性偏少,没有根据套管极限压强的产生机理构建其极限压强的公式,不同文献提出的理论公式存在相互矛盾或冲突;②有些假设和前提条件过于简化、苛刻和牵强,例如假定材料在弹性和塑性阶段皆为不可压缩,即假定泊松比ν=1/2[24],实际上,由热力学原理可以给出各向同性材料泊松比的取值范围为-1≤ν≤1/2;③没有严格区别闭端、开端和平面应变套管,应该分别解算这3种约束条件下的套管极限压强;④没有给出理论计算结果与公认权威试验数据或自己试验数据之间的绝对误差和相对误差。

本文采用俞茂宏统一强度理论分别求解了承受外压强时闭端、开端和平面应变套管弹塑性极限外压强的统一解,然后将理论计算结果与试验值进行了对比,验证了计算结果的准确性。

1 套管的弹性极限外压强

物体由于发生弹性形变而产生的力称为弹力。放在桌面上的水杯受到桌面对它的支持力,支持力是弹力;桌面受到水杯的压力,压力也是弹力。在物理学中,物体所受的压力与受力面积之比称为压强。考虑一个承受外压强p的套管,如图1所示,其内、外半径分别为ra和rb,塑性外边界半径为rp。

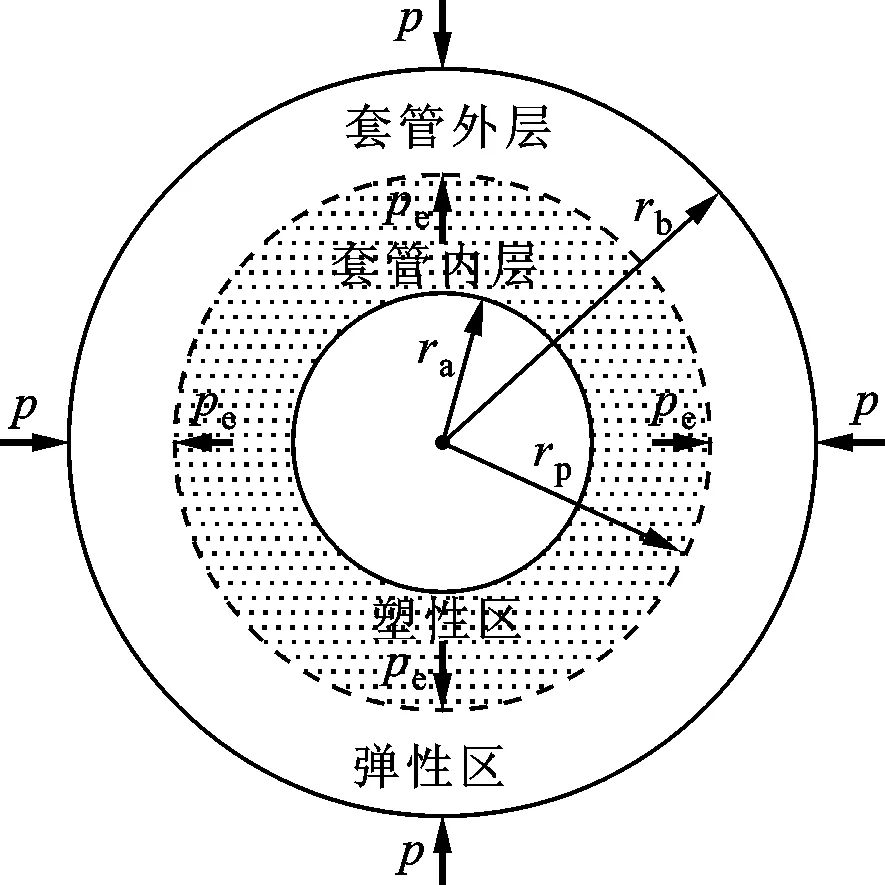
(b)弹性区和塑性区图1 承受外压强的套管

根据广义虎克定律,套管在弹性阶段的纵向应力

σz=Eεz+ν(σr+σθ)

(1)

式中:E为弹性模量;εz为纵向应变;σr为径向正应力;σθ为环向正应力。

拉梅弹性应力解为

(2)

(3)

如果套管上作用有纵向载荷F,则轴向应力

(4)

套管的3种约束条件为

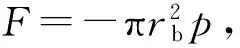
(5a)

F=0, 开端

(5b)

εz=0, 平面应变

(5c)

将式(5a)和(5b)分别代入式(4),得

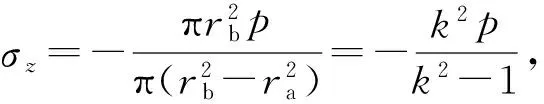
(6a)

σz=0, 开端

(6b)

式中:k为套管的外内半径比,k=rb/ra。

将式(2)(3)和(5c)代入式(1),得

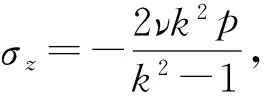
(6c)

将式(2)(3)和(6a)代入式(1),得

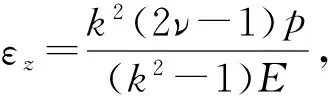
(7a)

将式(2)(3)和(6b)代入式(1),得

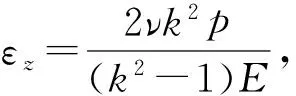
(7b)

由式(4)与式(6c)相等,得

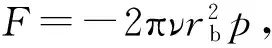
(7c)

由式(2)(3)和(6a)～(6c),得3种约束条件下的3个主应力

σ1=σr,σ2=σz,σ3=σθ, 闭端

(8)

由式(2)(3)(6a)和(8)得

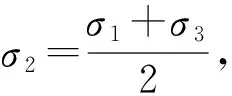
(9a)

由式(2)(3)(6b)和(8)得

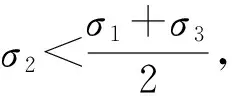
(9b)

由式(2)(3)(6c)和(8)得

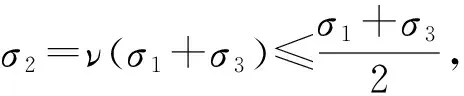
(9c)

对于0≤α≤1,以下不等式恒成立

(10)

双剪单元体由单剪单元体发展而来,其形成过程如图2所示。

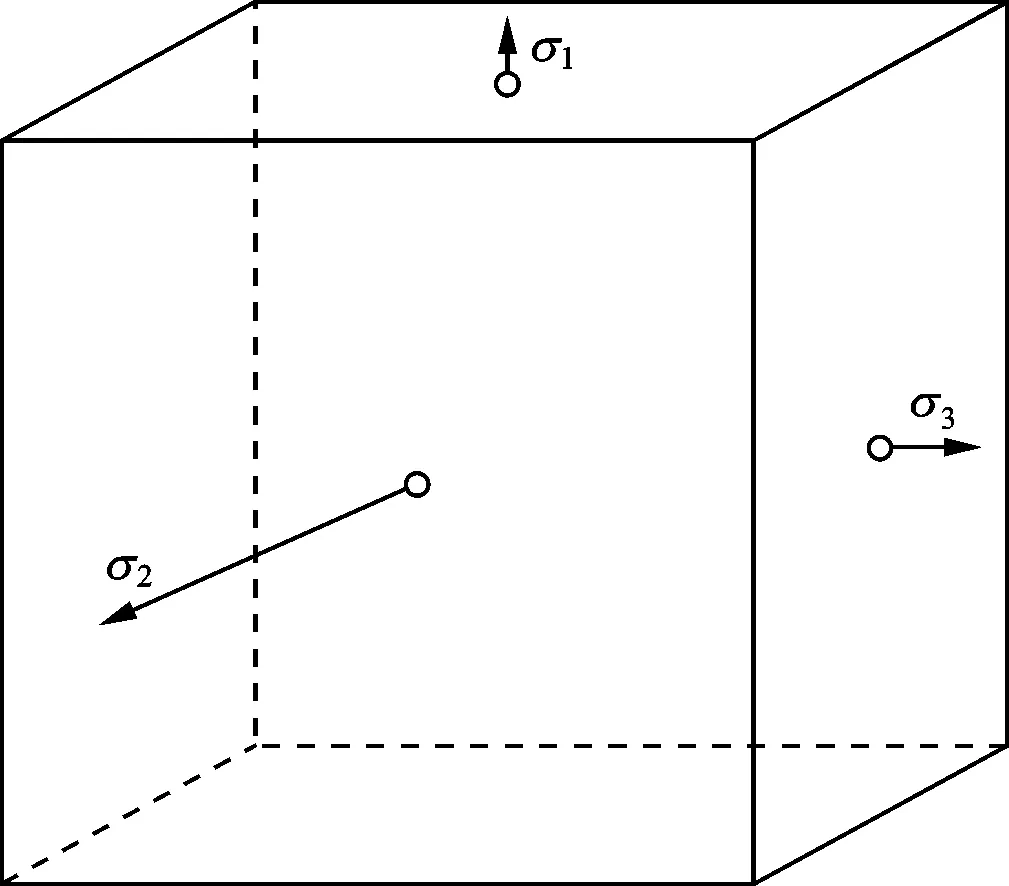
(a)主应力六面体单元体

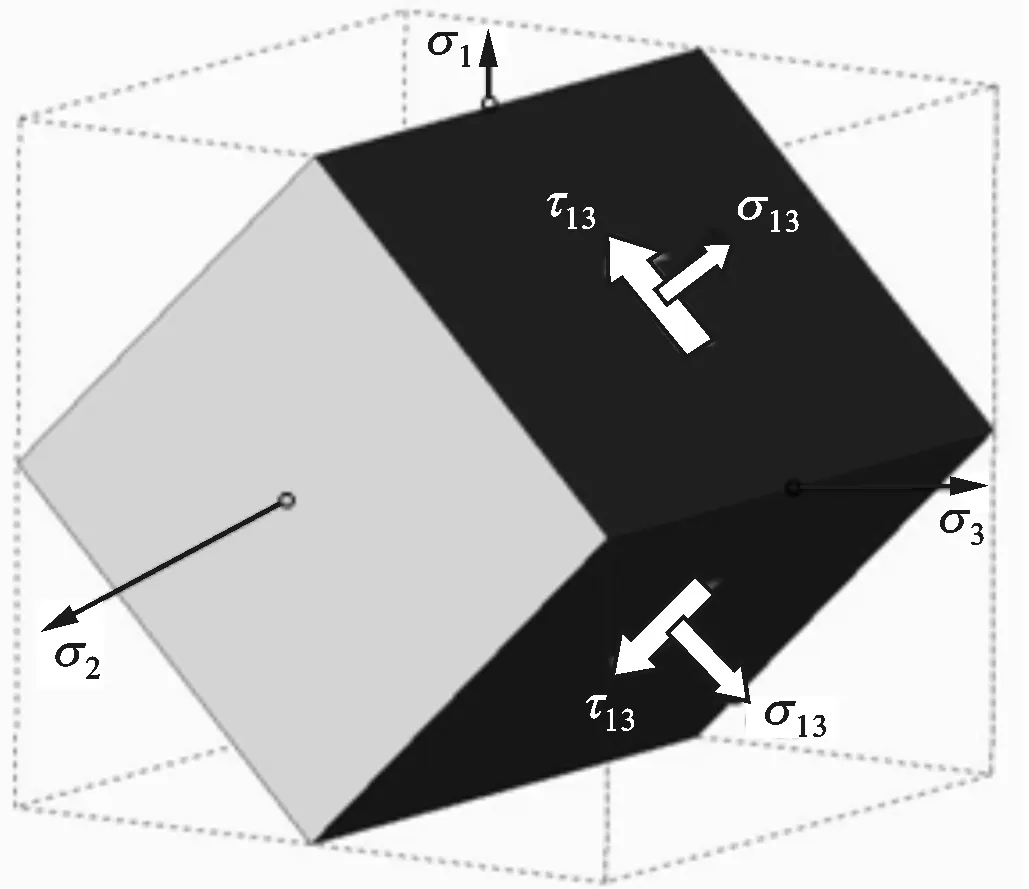
(b)同时与σ1和σ3成45°的单剪六面体单元体

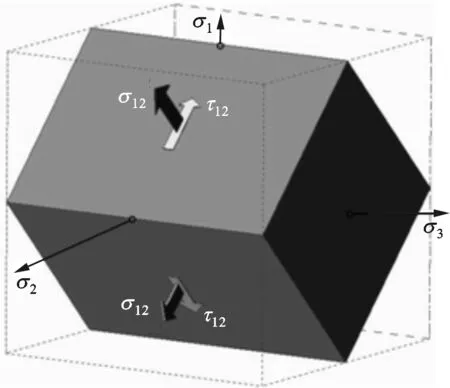
(c)同时与σ1和σ2成45°的单剪六面体单元体

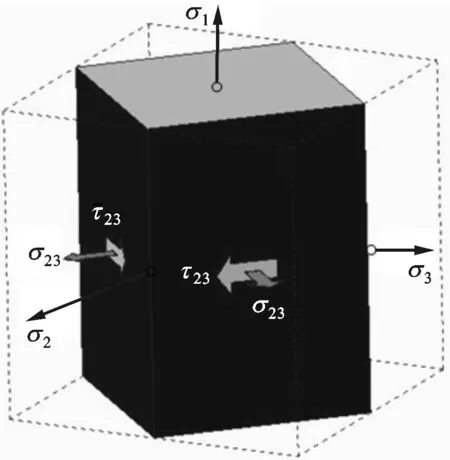
(d)同时与σ2和σ3成45°的单剪六面体单元体

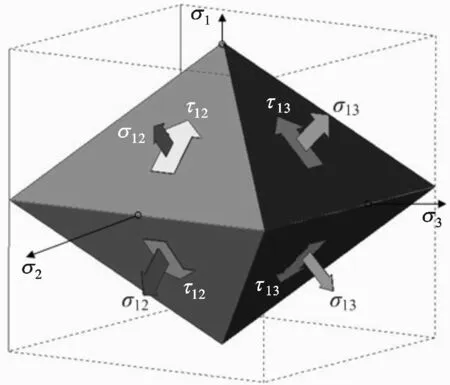
(e)在τ12作用时的双剪正交八面体单元体

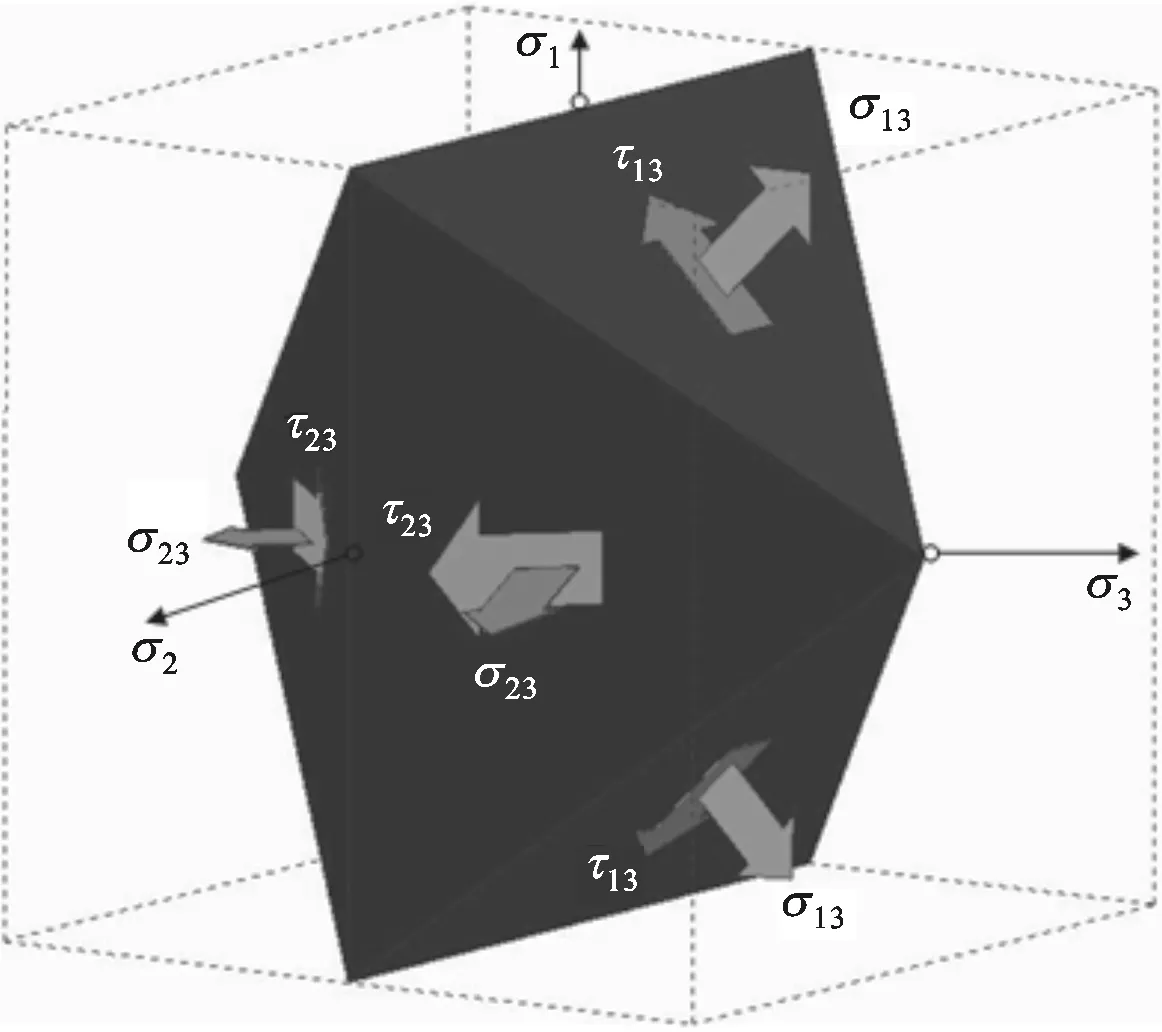
(f)在τ23作用时的双剪正交八面体单元体

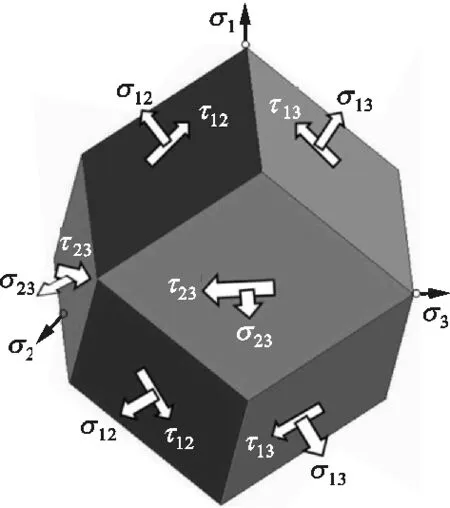
(g)三剪菱形十二面体单元体图2 应力单元体的形成过程

俞茂宏统一强度理论的2个数学表达式[25]为

(11a)

(11b)

式中:σt为抗拉强度。

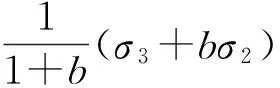
将式(8)和(9a)代入式(11a),得

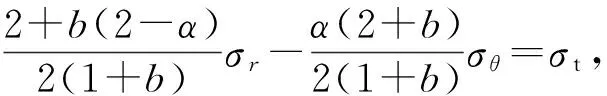
(12a)

将式(8)和(9b)代入式(11a),得

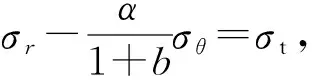
(12b)

将式(8)和(9c)代入式(11a),得

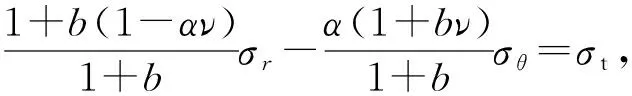
(12c)

将式(2)和(3)代入式(12a),得

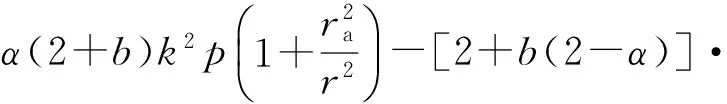
(13a)

将式(2)和(3)代入式(12b),得

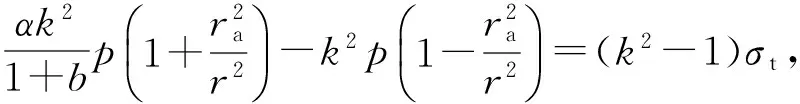
(13b)

将式(2)和(3)代入式(12c),得

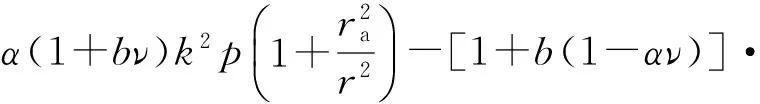
(13c)

令r=ra,由式(13a)～(13c),可得弹性极限外压强分别为

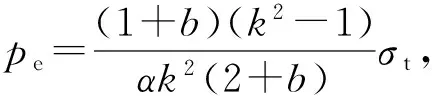
(14a)

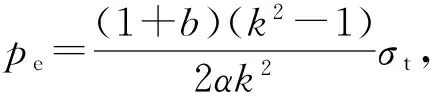
(14b)

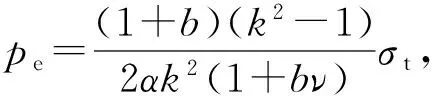
(14c)

对于拉压同性材料,α=1,由式(14a)得

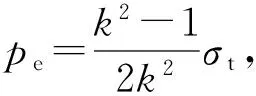
(15a)

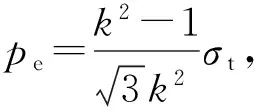
(15b)

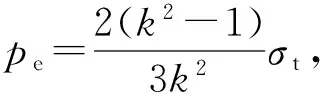
(15c)

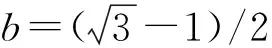
对于拉压同性材料,α=1,由式(14b)和(14c)分别得

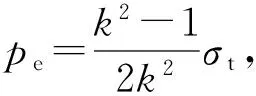
(16a)

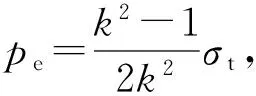
(16b)

令人惊奇的是,式(15a)(16a)与(16b)是一致的。

经典第四强度理论的屈服准则为

(17)

将式(2)(3)(6a)和(8)代入式(17),得

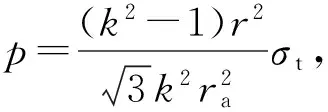
(18a)

将式(2)(3)(6b)和(8)代入式(17),得

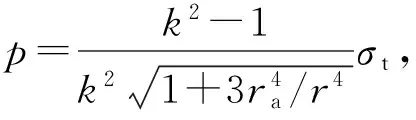
(18b)

将式(2)(3)(6c)和(8)代入式(17),得

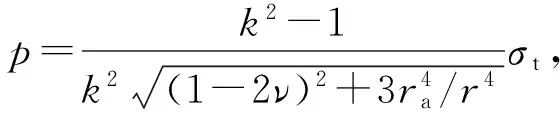
(18c)

设r=ra,由式(18a)～(18c),可得经典第四强度理论的弹性极限外压强分别为

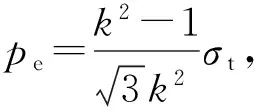
(19a)

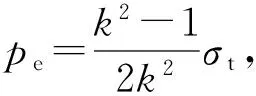
(19b)

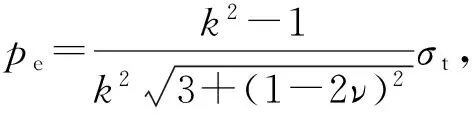
(19c)

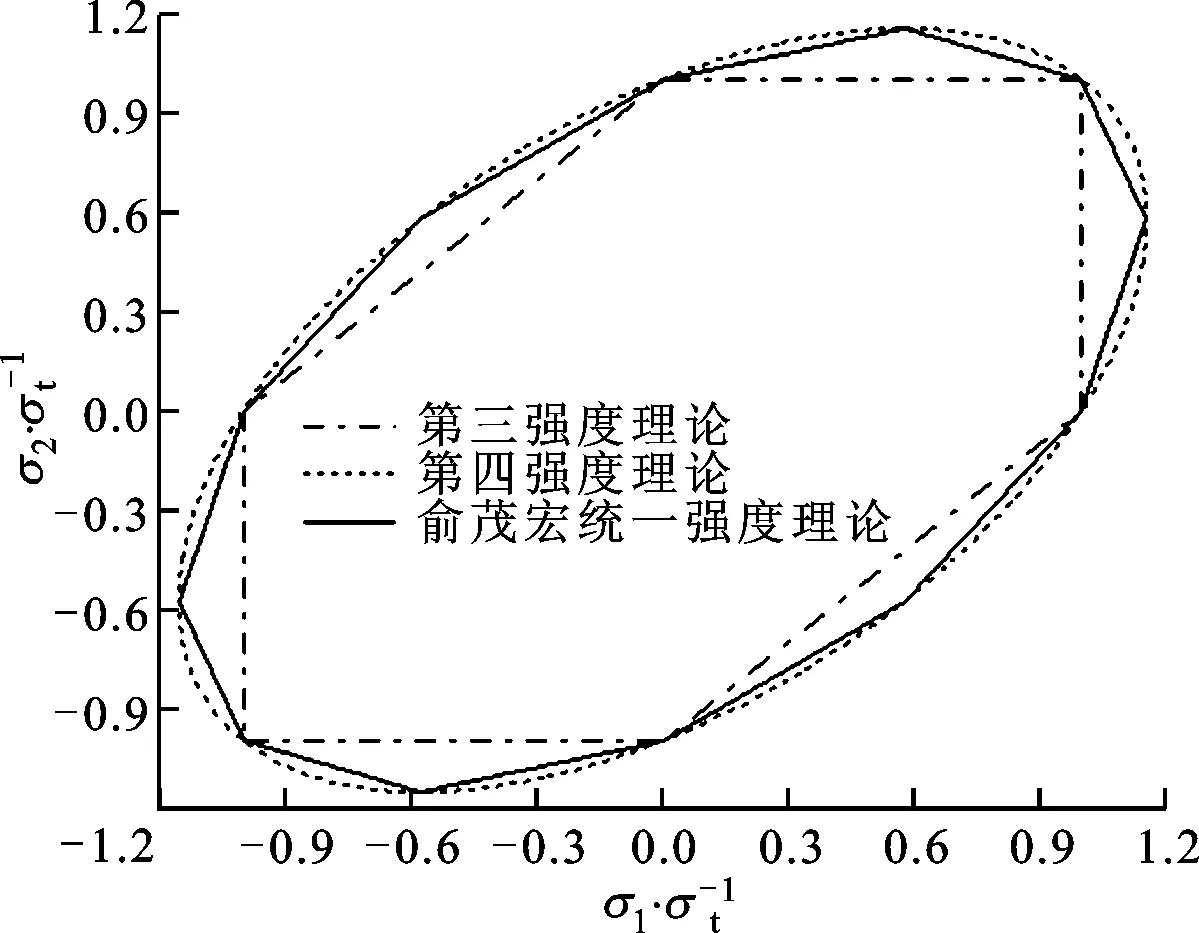
图3 3种强度理论对应的极限迹线

2 套管的塑性极限外压强

2.1 套管弹塑性阶段的弹性区分析

当作用于套管的外压强超过弹性极限外压强pe时,在套管的内壁将开始出现塑性区,并向外部扩展。当塑性区达到套管外表面时,套管的外压强达到最大值,即为塑性极限外压强。如图1b所示,弹性区的范围为rp≤r≤rb,在弹性区的内壁作用有压强pe,在外壁作用有压强p。

拉梅弹性应力解为

(20)

(21)

将式(5c)(20)和(21)代入式(1),得

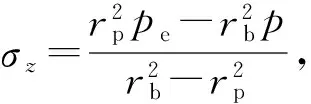
(22a)

σz=0, 开端

(22b)

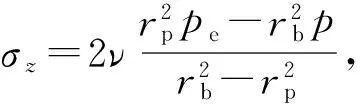
(22c)

将式(8)(20)(21)和(22a)代入式(11a),得

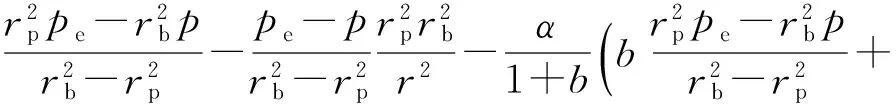
(23a)

将式(8)(20)(21)和(22b)代入式(11a),得

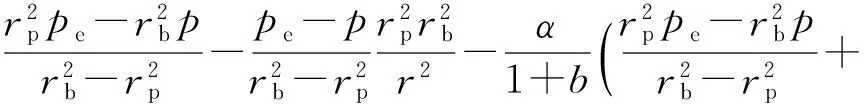
(23b)

将式(8)(20)(21)和(22c)代入式(11a),得

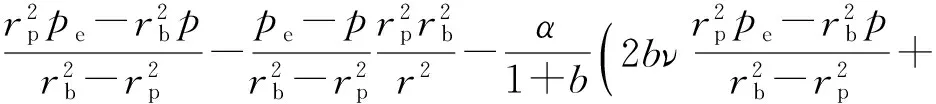
(23c)

令r=rp,由式(23a)～(23c)分别得

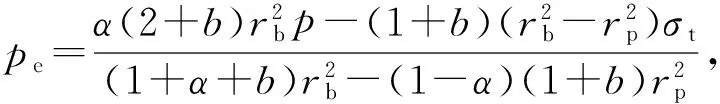
(24a)

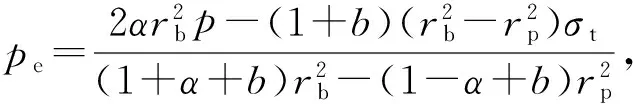
(24b)

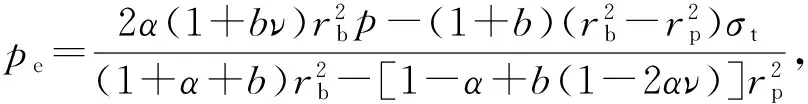
(24c)

2.2 套管弹塑性阶段的塑性区分析

如图1b所示,塑性区的范围为ra≤r≤rp,在塑性区的外壁作用有压强pe。在极坐标中,将微元体所受各力投影到微元体中心的径向轴上,得

(25)

由式(12a)～(12c)分别得

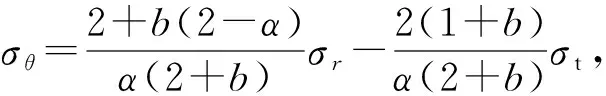
(26a)

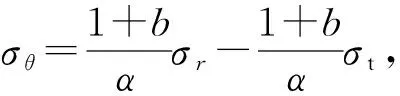
(26b)

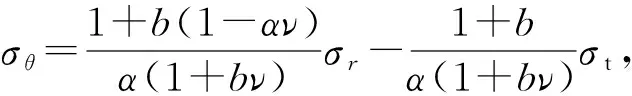
(26c)

将式(26a)代入式(25),得

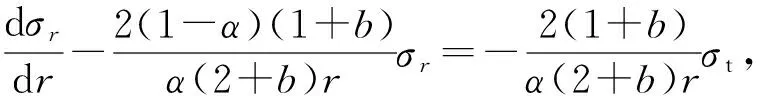
(27a)

将式(26b)代入式(25),得

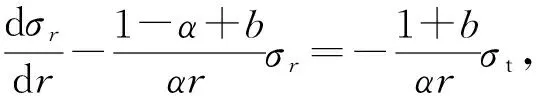
(27b)

将式(26c)代入式(25),得

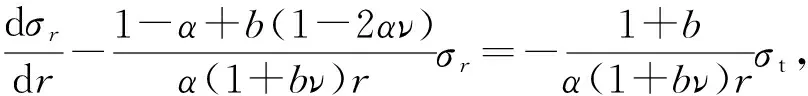
(27c)

一阶非齐次线性微分方程(27a)的通解为

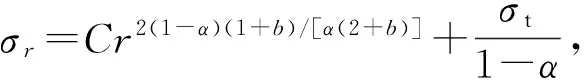
(28a)

式中:C为任意常数。

一阶非齐次线性微分方程(27b)的通解为

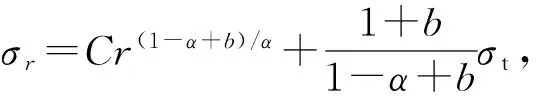
(28b)

一阶非齐次线性微分方程(27c)的通解为

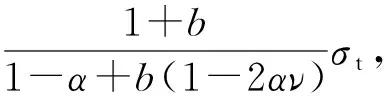
(28c)

边界条件为

σr|r=ra=0

(29)

将式(28a)～(28c)分别代入式(29),得

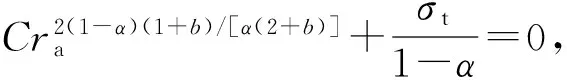
(30a)

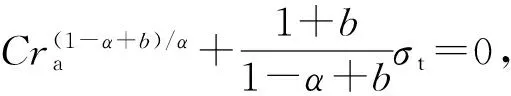
(30b)

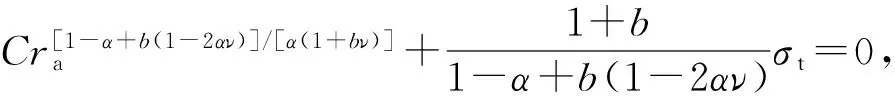
(30c)

由式(30a)～(30c)分别得

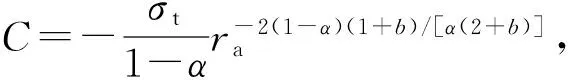
(31a)

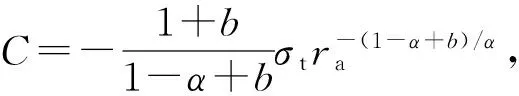
(31b)

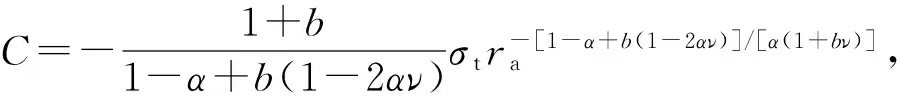
(31c)

将式(31a)～(31c)分别代入式(28a)～(28c),得

(32a)

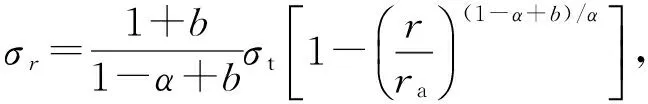
(32b)

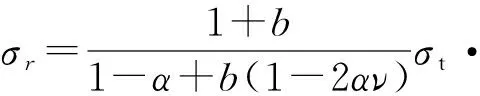
(32c)

将式(32a)～(32c)分别代入式(26a)～(26c),得

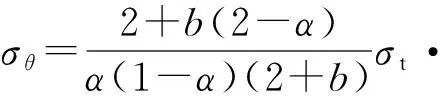
(33a)

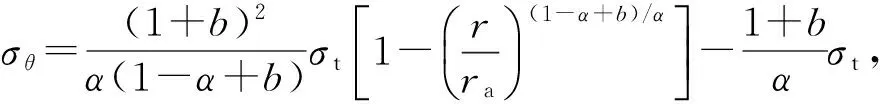
(33b)

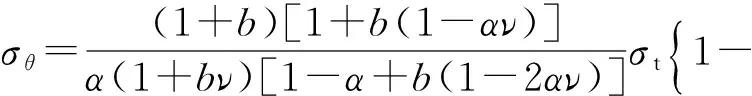
(33c)

2.3 套管弹塑性阶段的塑性区半径

径向正应力在塑性区半径rp处的连续性为

σr|r=rp(弹性区)=σr|r=rp(塑性区)

(34)

将式(20)(24a)和(32a)代入式(34),得

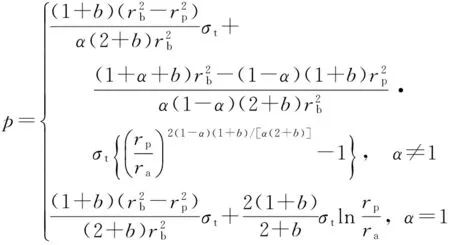
(35a)

将式(20)(24b)和(32b)代入式(34),得

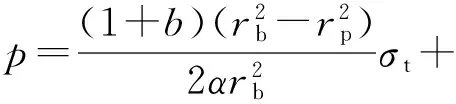
(35b)

将式(20)(24c)和(32c)代入式(34),得

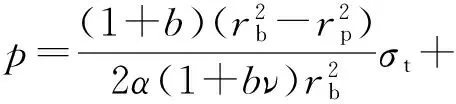
(35c)

由式(35a)～(35c)分别得

闭端

(36a)

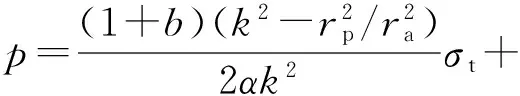
(36b)

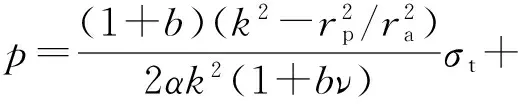
(36c)

2.4 套管的塑性极限外压强

当套管塑性区半径rp达到套管的外半径rb,即rp=rb时,套管处于完全塑性状态,由式(36a)～(36c),可得塑性极限外压强分别为

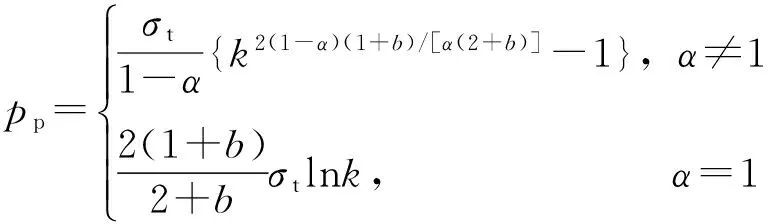
(37a)

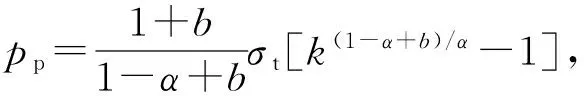
(37b)

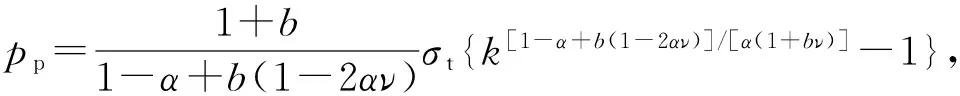
(37c)

将r=rb代入式(20)和(32a),也可得式(37a);将r=rb代入式(20)和(32b),也可得式(37b);将r=rb代入式(20)和(32c),亦可得式(37c)。

对于拉压同性材料,α=1,由式(37a)得

pp=σtlnk, 闭端(b=0,第三强度理论)

(38a)

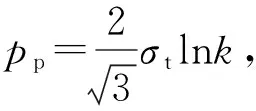
(38b)

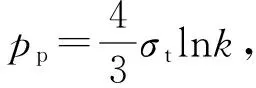
(38c)

式(38c)比式(38a)的计算值大33.33%,式(38c)比式(38b)的计算值大15.47%。令人惊奇的是,这2个数据与对式(15)的分析结果一样。俞茂宏统一强度理论与传统的单剪强度理论相比能更好地发挥材料的强度潜力,应用于工程可以使材料和结构的强度潜力提高15%～33%,可取得显著的经济效益。

对拉压同性材料,α=1,由式(37b)和(37c)得

pp=σtlnk, 开端(b=0,第三强度理论)

(39a)

pp=σtlnk, 平面应变(b=0,第三强度理论)

(39b)

同样,式(38a)(39a)与式(39b)也一致。

3 套管极限外压强的分析与讨论

3.1 拉压强度比对弹性极限外压强的影响

令泊松比ν=0.3。图4给出了一个外内半径比k=2的套管的弹性极限外压强与拉压强度比α和中间主应力系数b的关系,可见弹性极限外压强随拉压强度比的减小而增大,即抗压强度与抗拉强度之差越大,弹性极限外压强也越大;弹性极限外压强随中间主应力系数的增大而增大;开端套管的弹性极限外压强最大,平面应变套管的次之,闭端套管的最小。

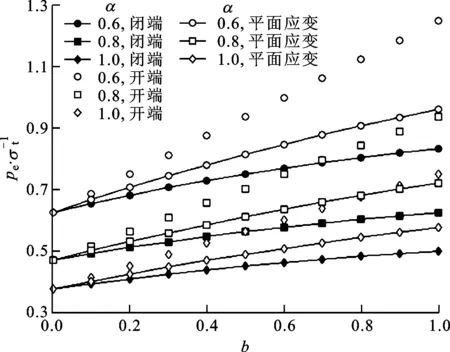
图4 弹性极限外压强与中间主应力系数的关系

3.2 外压强对塑性区半径的影响

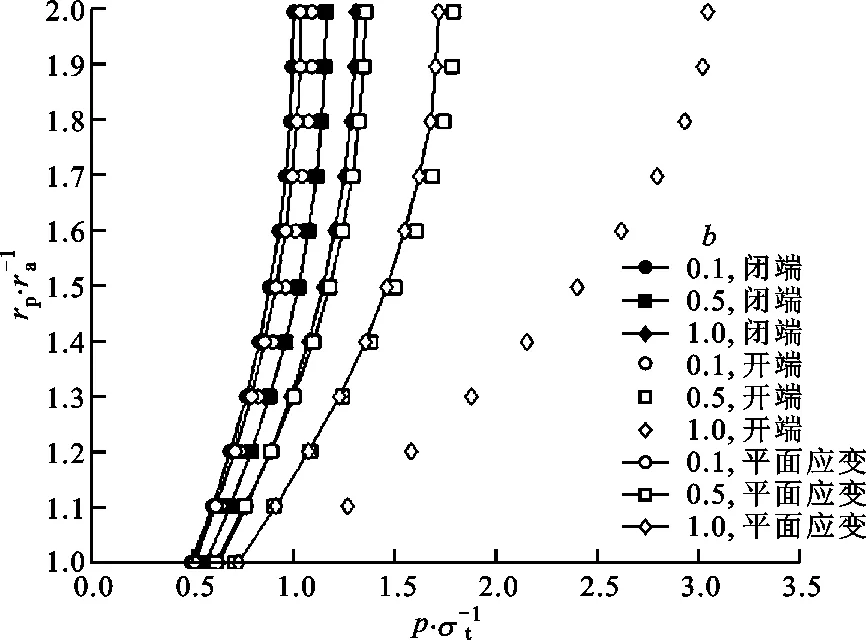
(a)塑性区半径与中间主应力系数的关系(α=0.8)

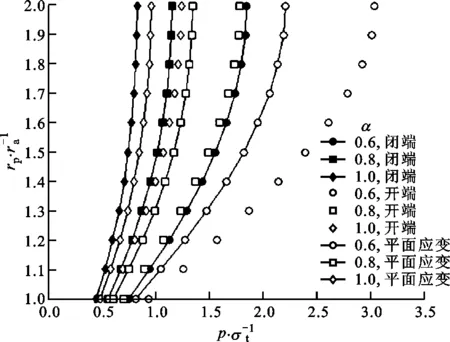
(b)塑性区半径与拉压强度比的关系(b=1/2)图5 塑性区半径与外压强的关系

令泊松比ν=0.3。图5给出了一个k=2的套管的rp与p、b、α的变化关系。由图5可知,rp随p的增大而增大。因为当rp=ra时,式(36a)变为式(14a),式(36b)变为式(14b),式(36c)变为式(14c),所以当p增大时,套管由弹性状态进入弹塑性状态,rp逐步从ra扩大到rb。由图5a可见,在同类条件(闭端、开端或平面应变)和相同外压强作用下,套管在b=1.0时的塑性区半径最小,在b=0.1时的塑性区半径最大;由图5b可见,在同类条件下,α=0.6时的塑性区半径最小,α=1.0时的塑性区半径最大。

3.3 中间主应力系数对塑性极限外压强的影响

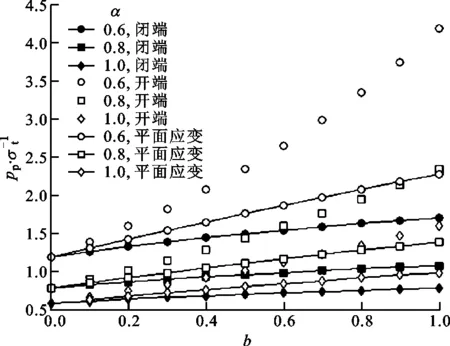
(a)k=1.8

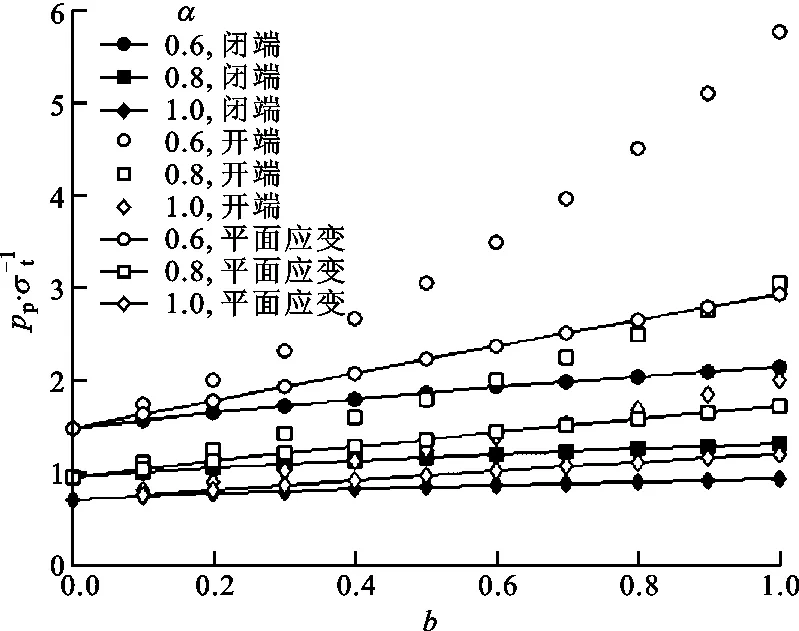
(b)k=2.0

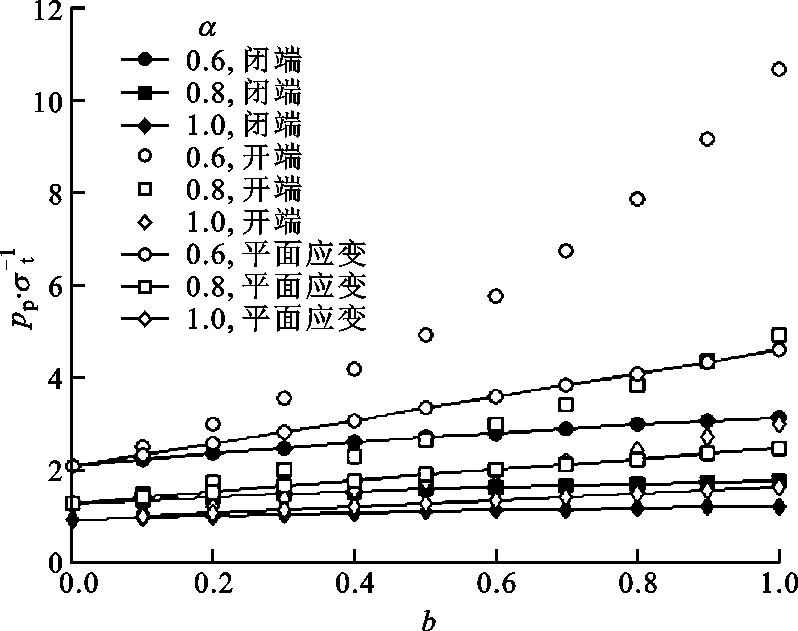
(c)k=2.5

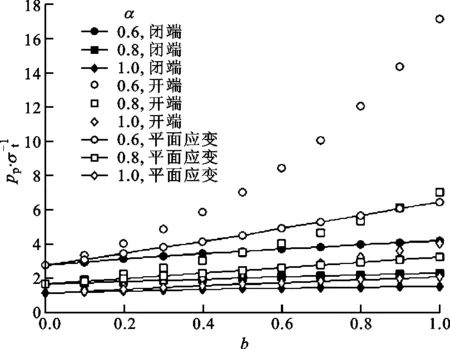
(d)k=3.0图6 塑性极限外压强与中间主应力系数的关系

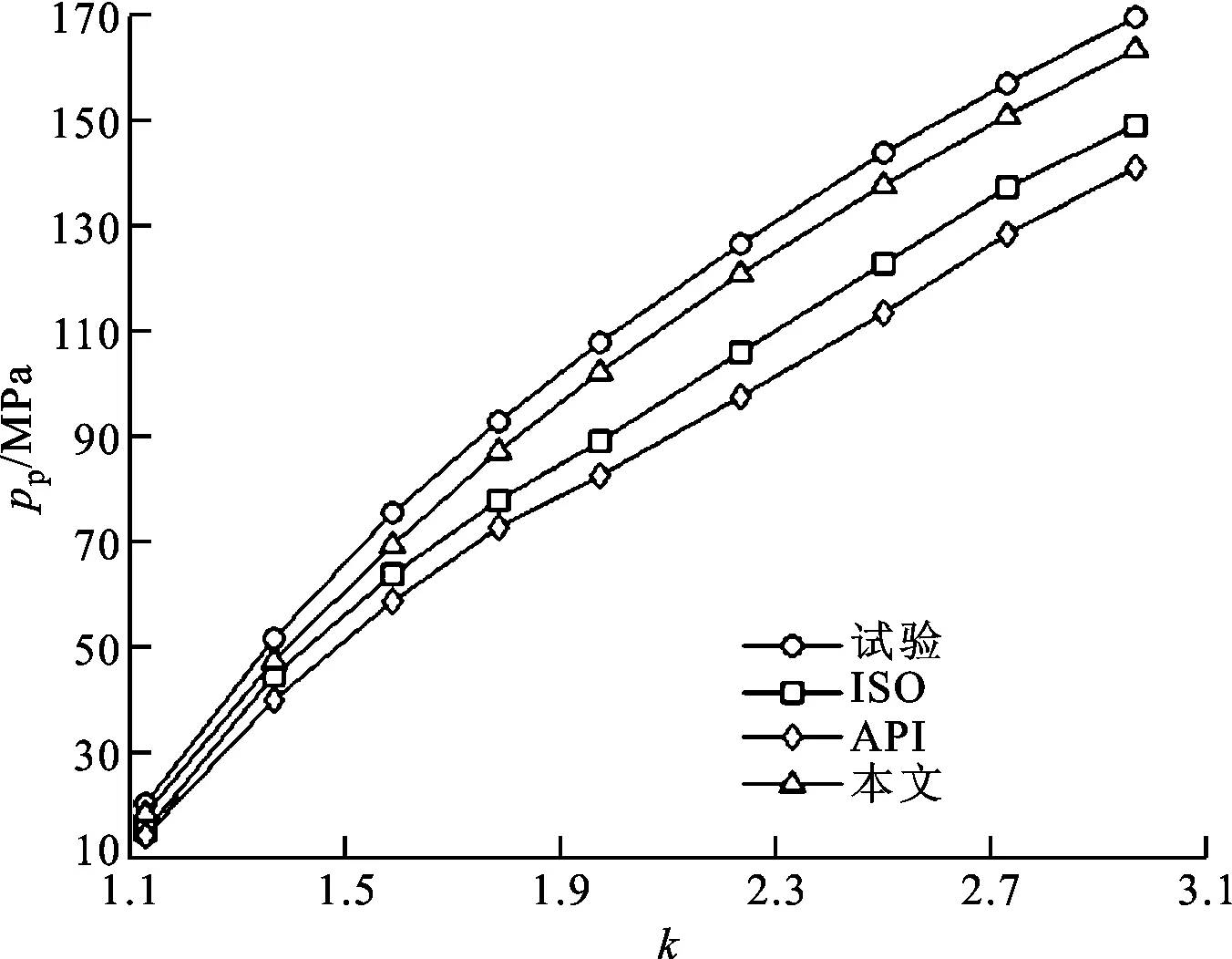
图7 本文计算值、ISO和API推荐数据与试验值的对比

令泊松比ν=0.3。具有不同外内半径比的套管的塑性极限外压强与中间主应力系数的关系如图6所示,可见塑性极限外压强随拉压强度比的减小而增大,即抗压强度与抗拉强度的差越大,塑性极限外压强越大;随外内半径比的增大,在相同参数下,闭端、开端和平面应变套管塑性极限外压强之间的差异增大。对比图4与图6b可知,套管的塑性极限外压强大于弹性极限外压强。

4 试验验证

图7显示了本文的塑性极限外压强计算值、国际标准化组织(ISO)样板数据[26]、美国石油协会(API)推荐数据[27]与试验测试数据[28]的比较情况,可见本文的计算值最接近试验值,而ISO和API的数据皆远远小于试验值。通过分析可知,双剪屈服准则对应公式(38c)的计算值可作为塑性极限外压强设计的上限。

图7中本文、ISO和API的塑性极限外压强计算数据与试验测试数据的相对误差见表1,可见本文的计算值与试验测试值之间的相对误差在-4%～-9%的范围内,相对误差最小;ISO样板数据与试验测试值之间的相对误差在-12%～-25%的范围内,相对误差较大;API推荐数据与试验测试值之间的相对误差在-17%～-30%的范围内,相对误差最大。

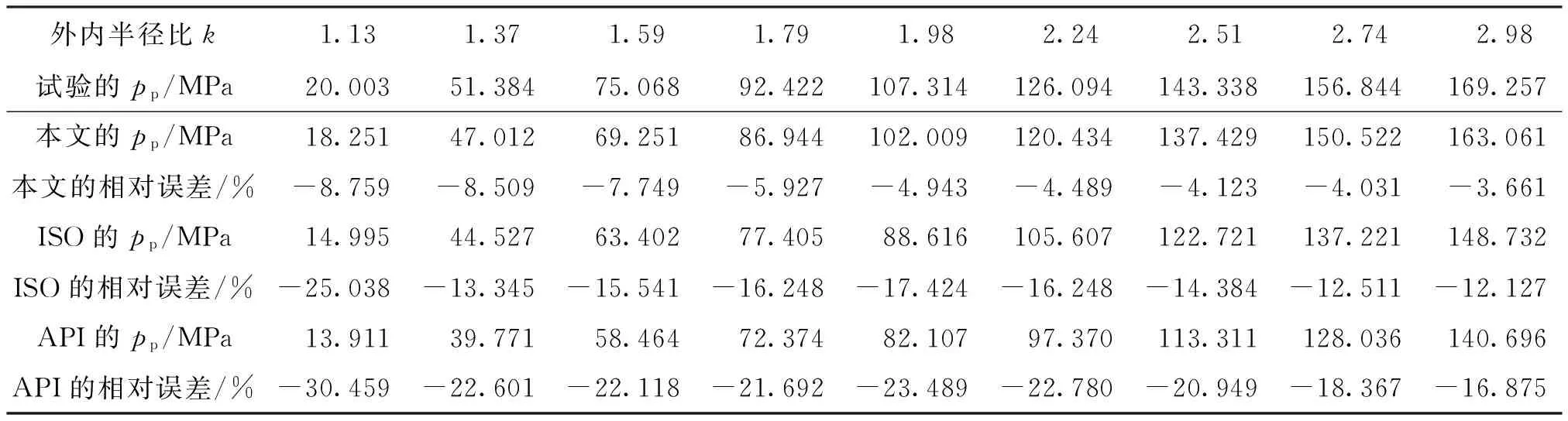
表1 本文和2个机构的塑性极限外压强与试验值的定量误差

5 结 论

本文采用俞茂宏统一强度理论求解了承受外压强时闭端、开端和平面应变套管弹塑性极限外压强的统一解,分析了塑性区半径的作用,获得的具体结论如下。

(1)推导出了承受外压强时闭端、开端和平面应变套管弹性与塑性极限外压强的统一解。

(2)弹性极限外压强随拉压强度比的减小而增大,随中间主应力系数的增大而增大;开端套管的弹性极限外压强最大,平面应变套管的次之,闭端套管的最小。

(3)塑性区的半径随外压强的增大而增大;当外压强增大时,套管由弹性状态进入弹塑性状态,塑性区的半径逐步从内半径扩大到外半径。

(4)塑性极限外压强随拉压强度比的减小而增大;随外内半径比的增大,在相同的统一强度理论参数下,闭端、开端和平面应变套管塑性极限外压强之间的差异增大;套管的塑性极限外压强大于弹性极限外压强。

参考文献:

[1] YU Maohong. Twin shear stress yield criterion [J]. Elsevier International Journal of Mechanical Sciences, 1983, 25(1): 71-74.

[2] 俞茂宏, 宋凌宇, 陈萍. 双剪应力准则的一个推广 [J]. 西安交通大学学报, 1983, 17(3): 65-69.

YU Maohong, SONG Lingyu, CHEN Ping. A generalization of the twin-shear-stress-yield-criterion [J]. Journal of Xi’an Jiaotong University, 1983, 17(3): 65-69.

[3] 俞茂宏, 何丽南, 宋凌宇. 双剪应力强度理论及其推广 [J]. 中国科学: A辑, 1985, 28(12): 1113-1120.

[4] YU Maohong, HE Linan, SONG Lingyu. Twin shear stress theory and its generalization [J]. Scientia Sinica: Series A, 1985, 28(11): 1174-1183.

[5] 俞茂宏, 何丽南, 刘春阳. 广义双剪应力屈服准则及其推广 [J]. 科学通报, 1992, 37(2): 182-185.

[6] YU Maohong. Advances in strength theories for materials under complex stress state in the 20th century [J]. ASME Applied Mechanics Reviews, 2002, 55(3): 169-218.

[7] 张智, 刘志伟, 谢玉洪, 等. 井筒载荷-腐蚀耦合作用对碳钢套管服役寿命的影响 [J]. 石油学报, 2017, 38(3): 342-347, 362.

ZHANG Zhi, LIU Zhiwei, XIE Yuhong, et al. Influence of shaft load-corrosion coupling on the service life of carbon steel casing pipe [J]. Acta Petrolei Sinica, 2017, 38(3): 342-347, 362.

[8] 张微敬, 郭媛媛, 刘时伟. 钢筋套筒挤压连接的预制RC柱抗震性能试验研究 [J]. 工程力学, 2016, 33(12): 119-127.

ZHANG Weijing, GUO Yuanyuan, LIU Shiwei. Experimental research on seismic behavior of precast RC columns with steel bars spliced by compressive sleeves [J]. Engineering Mechanics, 2016, 33(12): 119-127.

[9] 杨睿月, 黄中伟, 李根生, 等. 连续油管带筛管双重管柱岩屑运移模型研究 [J]. 中国石油大学学报(自然科学版), 2016, 40(5): 87-95.

YANG Ruiyue, HUANG Zhongwei, LI Gensheng, et al. Slotted liner sheathing coiled tubing: a dual-pipe model for cuttings transport [J]. Journal of China University of Petroleum(Edition of Natural Science), 2016, 40(5): 87-95.

[10] 刘波, 刘璐璐, 徐薇, 等. 基于统一强度理论的TBM斜井围岩弹塑性解 [J]. 采矿与安全工程学报, 2016, 33(5): 819-826.

LIU Bo, LIU Lulu, XU Wei, et al. Elastic-plastic analytical solution of TBM inclined shaft based on unified strength criterion [J]. Journal of Mining & Safety Engineering, 2016, 33(5): 819-826.

[11] 朱瑞林, 朱国林. 热预应力自增强厚壁圆筒研究 [J]. 机械工程学报, 2016, 52(17): 168-175.

ZHU Ruilin, ZHU Guolin. Study on autofrettaged thick-walled cylinders with thermal pre-stresses [J]. Journal of Mechanical Engineering, 2016, 52(17): 168-175.

[12] 陈梁, 茅献彪, 李明, 等. 基于Drucker-Prager准则的深部巷道破裂围岩弹塑性分析 [J]. 煤炭学报, 2017, 42(2): 484-491.

CHEN Liang, MAO Xianbiao, LI Ming, et al. Elastoplastic analysis of cracked surrounding rock in deep roadway based on Drucker-Prager criterion [J]. Journal of China Coal Society, 2017, 42(2): 484-491.

[13] FANG Jun, WANG Yanbin, GAO Deli. On the collapse resistance of multilayer cemented casing in directional well under anisotropic formation [J]. Elsevier Journal of Natural Gas Science and Engineering, 2015, 26: 409-418.

[14] DENG Kuanhai, LIN Yuanhua, QIANG Hu, et al. New high collapse model to calculate collapse strength for casing [J]. Elsevier Engineering Failure Analysis, 2015, 58: 295-306.

[15] 刘奎, 高德利, 王宴滨, 等. 局部载荷对页岩气井套管变形的影响 [J]. 天然气工业, 2016, 36(11): 76-82.

LIU Kui, GAO Deli, WANG Yanbin, et al. Effects of local load on shale gas well casing deformation [J]. Natural Gas Industry, 2016, 36(11): 76-82.

[16] 李宁波, 钱稼茹, 刘时伟, 等. 部分竖向分布钢筋套筒挤压连接的预制剪力墙抗震性能试验研究 [J]. 土木工程学报, 2016, 49(7): 36-48.

LI Ningbo, QIAN Jiaru, LIU Shiwei, et al. Experimental study on seismic behavior of pre-cast shear walls with partial vertical distributed steel bars pressed sleeve splicing [J]. China Civil Engineering Journal, 2016, 49(7): 36-48.

[17] 齐昌广, 刘汉龙, 陈永辉, 等. 塑料套管混凝土桩承载试验及沉降计算方法研究 [J]. 岩土工程学报, 2016, 38(12): 2302-2308.

QI Changguang, LIU Hanlong, CHEN Yonghui, et al. Bearing capacity tests and settlement calculation method of plastic tube cast-in-place concrete pile [J]. Chinese Journal of Geotechnical Engineering, 2016, 38(12): 2302-2308.

[18] 曹雪叶, 赵均海, 张常光. 基于统一强度理论的冻结壁弹塑性应力分析 [J]. 岩土力学, 2017, 38(3): 769-774, 809.

CAO Xueye, ZHAO Junhai, ZHANG Changguang. Elastoplastic stress analysis of frozen soil wall based on unified strength theory [J]. Rock and Soil Mechanics, 2017, 38(3): 769-774, 809.

[19] YIN Fei, GAO Deli. Prediction of sustained production casing pressure and casing design for shale gas horizontal wells [J]. Elsevier Journal of Natural Gas Science and Engineering, 2015, 25: 159-165.

[20] HUANG Wenjun, GAO Deli. A theoretical study of the critical external pressure for casing collapse [J]. Elsevier Journal of Natural Gas Science and Engineering, 2015, 27: 290-297.

[21] XU S Q, YU M H. The effect of the intermediate principal stress on the ground response of circular openings in rock mass [J]. Springer Rock Mechanics and Rock Engineering, 2006, 39(2): 169-181.

[22] CHEN Zhanfeng, ZHU Weiping, DI Qinfeng, et al. Numerical and theoretical analysis of burst pressures for casings with eccentric wear [J]. Elsevier Journal of Petroleum Science and Engineering, 2016, 145: 585-591.

[23] ZHANG Hongkun, SUN Baojiang, YAN Guomin, et al. Distribution laws and effects analysis of casing external pressure taking elastic parameters matching into account [J]. Elsevier Petroleum, 2016, 2(1): 108-115.

[24] 林元华, 邓宽海, 孙永兴, 等. 基于统一强度理论的套管全管壁屈服挤毁压力 [J]. 石油勘探与开发, 2016, 43(3): 462-468.

LIN Yuanhua, DENG Kuanhai, SUN Yongxing, et al. Through-wall yield collapse pressure of casing based on unified strength theory [J]. Petroleum Exploration and Development, 2016, 43(3): 462-468.

[25] 田红亮, 彭文昱, 何孔德, 等. 采用俞茂宏统一强度理论求解圆筒和球壳的极限值 [J]. 西安交通大学学报, 2018, 52(3): 1-11.

TIAN Hongliang, PENG Wenyu, HE Kongde, et al. Solving limit values of cylinder and spherical shell adopting Yu’s unified strength theory [J]. Journal of Xi’an Jiaotong University, 2018, 52(3): 1-11.

[26] Petroleum and natural gas industries: formulae and calculation for casing, tubing, drill pipe and line pipe properties: ISO 10400 [S]. 6th ed. Geneva, Switzerland: International Organization for Standardization, 2007.

[27] Bulletin on formulas and calculations for casing, tubing, drill pipe, and line pipe properties: API Bulletin 5C3 [S]. 6th ed. Washington, USA: American Petroleum Institute, 1994.

[28] ASBILL W T, CRABTREE S, PAYNE M L. DEA-130 modernization of tubular collapse performance properties [R]. San Antonio, USA: Southwest Research Institute, 2002.

[本刊相关文献链接]

陈保家,汪新波,严文超,等.采用品质因子优化和子带重构的共振稀疏分解滚动轴承故障诊断方法.2018,52(4):70-76.[doi:10.7652/xjtuxb201804010]

田红亮,彭文昱,何孔德,等.采用俞茂宏统一强度理论求解圆筒和球壳的极限值.2018,52(3):1-10.[doi:10.7652/xjtuxb201803001]

田红亮,董元发,钟先友,等.圆锥微凸体在粗糙表面接触分析中的应用.2017,51(11):71-78.[doi:10.7652/xjtuxb2017 11011]

马朝,何雅玲,袁帆,等.高温套管式熔融盐相变蓄热器蓄热性能实验研究.2017,51(5):1-8.[doi:10.7652/xjtuxb2017 05001]

田红亮,郑金华,陈甜敏,等.直线运动滚动导轨副的法向接触力学模型.2016,50(5):1-11.[doi:10.7652/xjtuxb201605 001]

李乃一,彭宗仁,刘鹏.直流电压下环氧浇注绝缘子的表面电场分析.2016,50(2):73-79.[doi:10.7652/xjtuxb201602013]

田红亮,陈甜敏,郑金华,等.平行轴圆柱副接触分析.2016,50(1):8-15.[doi:10.7652/xjtuxb201601002]

田红亮,赵美云,郑金华,等.新的柔性结合部法向接触刚度和接触阻尼方程.2015,49(1):118-126.[doi:10.7652/xjtuxb201501020]

张施令,彭宗仁,刘鹏.特高压干式油气套管内绝缘结构的优化设计.2014,48(8):116-121.[doi:10.7652/xjtuxb201408 020]