迷宫型声学超表面可调参数及其全相位调节
2018-05-16侯明明吴九汇
侯明明, 吴九汇
(1.西安交通大学机械工程学院, 710049, 西安;2.西安交通大学机械结构强度与振动国家重点实验室, 710049, 西安)
近20年来,声学超材料[1-5]得到了人们的广泛关注,声学超表面[6]已经成为声学超材料领域的研究热点。超表面最早是在电磁波领域发展起来的,随后扩展到声学领域。Li等制作了用于反射声波调控的声学超表面,并在此基础上实现了声学超棱镜[7]。Zhao等提出了通过非均匀阻抗及可调控的反常声波反射来操控声波波前的方法[8],并且通过所提出的声学超表面实现了声波的重新定向[9]。Ma等通过实验实现了具有低频完美吸声能力的声学超表面[10]。Xie等通过迷宫型声学超表面,实现了波前调控和亚波长声衍射[11]。从2014年开始,声学超表面已经引起了研究人员的广泛关注,也取得了丰硕的研究成果,同时还有部分学者探索了声学超表面在声学隐身等方面的应用[12-14]。
迷宫结构是以不同于局域共振型声学超材料的方式来实现亚波长声学特性的新型声学超材料结构。Liang等在2012年首次提出了一种二维空间卷曲的迷宫型声学超材料,可以实现双负等效材料参数、准零质量和较大的折射率,属于一种非共振式亚波长结构[15]。Xie等通过实验验证了迷宫型声学超材料的宽频负折射特性[16]。Li Yong等提出一种超薄的迷宫型声学超材料,实现了非凡的声透射和声波波前幅值及相位的调控[17]。Frenzel等设计了三维迷宫型声学超材料,并通过实验表明,在1~4 kHz的宽频范围内相速度和群速度都比在空气中低约8倍[18]。Cai等采用3D打印技术制作了迷宫型声学超材料,获得了优异的共振吸声效果[19]。Li Jing等设计了一种含有多层开缝管道的赫姆霍兹共振声子晶体,得到了比较宽的低频带隙[20]。Guan等提出了一种赫姆霍兹共振结构,获得了较好的低频降噪效果[21]。Li Yong等提出了一种具有完美吸声能力的迷宫型声学超表面,对所建模型的声阻抗进行了理论推导,并进行了仿真验证[22],但不足之处是对各个参数与完美吸声器间的关系没有进行深入细致的分析,且没有提及声学超表面对反射相位的调节作用。
本文提出了一种穿孔型迷宫声学超表面结构,深入细致地分析了各个几何参数与该声学超表面的关系和声学超表面对反射相位的调节作用,揭示了声学超表面与各个参数之间的内在联系,逐个剖析了每个可调参数影响声学超表面吸声系数和反射相位的物理机理。最后,设计了一种具有10个超表面原胞、结构简单紧凑的迷宫型周期结构,实现了从0到2π跨度上的相位调节。
1 模型及验证
本文设计的亚波长迷宫型声学超表面可以看作是由多个超表面原胞构成的超薄二维阵列平面,而超表面原胞则由1个迷宫和1个穿孔盖板构成,如图1所示。这种结构小巧紧凑,可以显著减小系统的厚度。
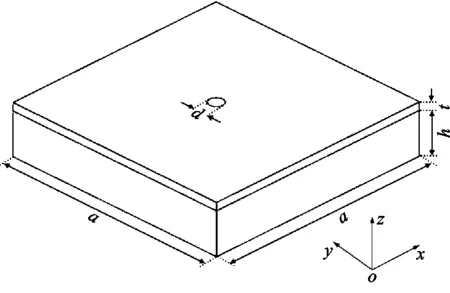
(a)声学超表面原胞三维图
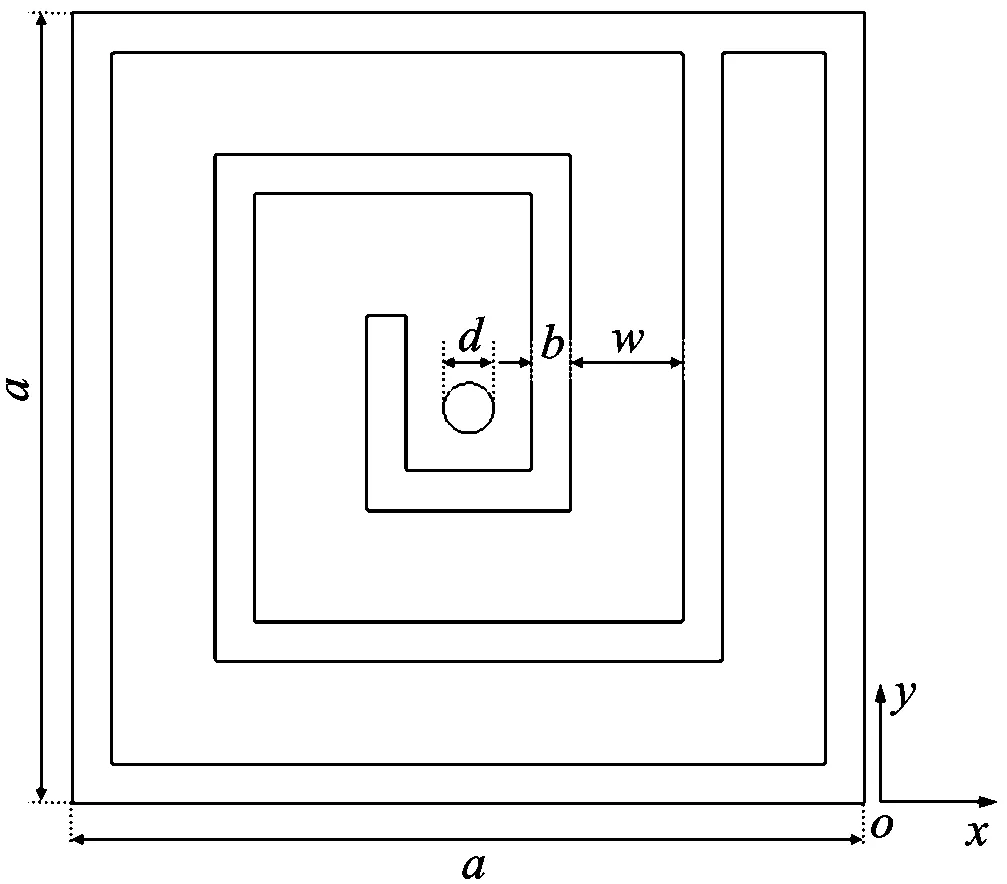
(b)声学超表面原胞二维图图1 声学超表面原胞的三维和二维图
图1中,a为超表面原胞的边长,d为迷宫盖板的小孔直径,w为迷宫槽宽,b为迷宫棱宽,t为盖板的厚度,h为迷宫槽深。本文所设计的迷宫型声学超表面结构由完全相同的超表面原胞周期性排列而成。为了方便,选取超表面原胞为对象来研究迷宫型声学超表面结构的物理现象及其机理。
在一般情况下,这种迷宫型声学超表面系统边界的声学特性阻抗Zs=Rs+iYs,其中Rs和Ys分别为声阻和声抗。声阻就是小孔声阻,主要由小孔直径决定;声抗由小孔声抗(取决于小孔直径)和迷宫内空气腔的声抗(取决于空气腔的有效长度)共同决定[22]。空气阻抗Za=ρ0c0/S,其中ρ0和c0分别为空气密度和空气中的声速,S是入射端声学超表面原胞的面积。这种边界下的吸声系数[20]
(1)
式(1)表明,吸声系数α=1(声完全吸收)需要同时满足2个条件:①Ys=0,表示共振状态;②Rs=1,表示阻抗匹配。α=1意味着声能量被声阻完全耗散。假定入射波沿着负z轴方向射入声学超表面结构,并穿透小孔到达迷宫内空气腔,其相位
(2)
为了验证本文所建模型的正确性,首先采用Li Yong模型的几何参数[22],即h=10 mm,w=12 mm,a=100 mm,b=1 mm,d=3.3 mm,t=0.2 mm。取空气密度为1.21 kg/m3,声速为343 m/s,动力黏度为15.6 μPa·s。迷宫材料为环氧树脂,迷宫盖板材料为不锈钢,材料参数见表1。利用商业有限元软件COMSOL MultiphysicsTM4.3b,对本文所建模型的吸声系数进行仿真计算,平面波辐射边界条件加在入射声波的边界,周期性边界条件加在y方向,以便计算反射波相位的幅值。仿真结果如图2所示,可见本文模型与Li Yong模型的吸声系数曲线几乎重合,从而证明了本文模型的正确性,而存在偏差是由于仿真中能量方程采用了简化的声特性阻抗。
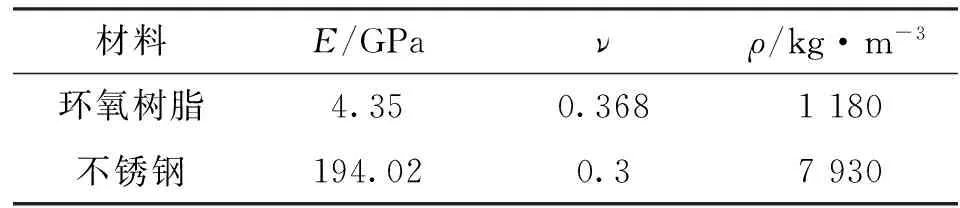
表1 声学超表面原胞的材料参数
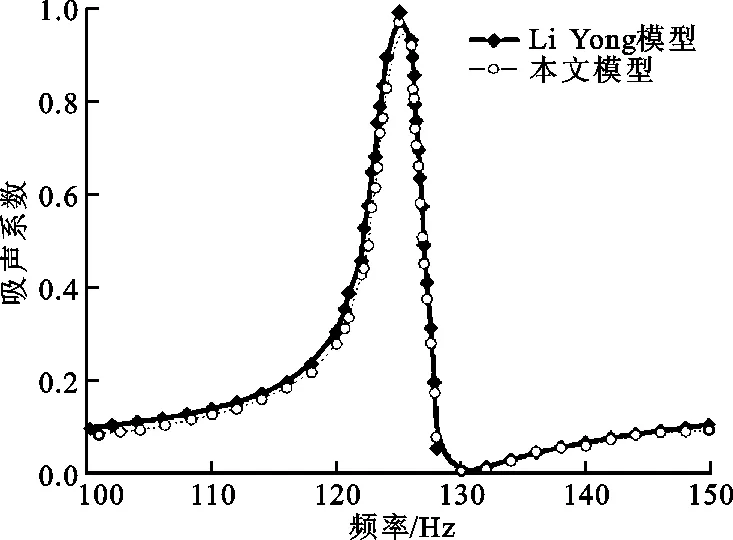
图2 系统吸声系数与频率的关系曲线
为了解考虑和不考虑固体对声学超表面结构物理特性的影响,分别计算了在声固耦合和压力声学2种情况下迷宫结构的吸声系数α(α=1-R2,其中R为反射系数)和反射相位,结果如图3所示。由图3可知,当其他条件(材料参数见表1,几何参数见表2)相同时,声固耦合情况下吸声系数达到峰值的频率要比压力声学情况下的频率低一些,这一现象说明,柔性固体结构对迷宫型超表面物理特性(吸声系数和反射相位)有很大的影响。

表2 声学超表面原胞的几何参数 mm
图3a表明,在很多频段吸声系数都达到了最大值,这是由于声学超表面通过干涉具有适当频段相位和振幅的入射波来消除共振频率处的散射波,从而实现了声波的完全吸收。图3b显示出声固耦合和压力声学2种情况下反射相位随频率的变化情况,可见低频段相位变化不大,但在高频段声固耦合情况下的共振频率要比压力声学的低一些,而且相位变化要大一些,这是由于声固耦合使系统的共振频率降低,高频段相位变化的灵敏度提高,是由声波的频率特性决定的。
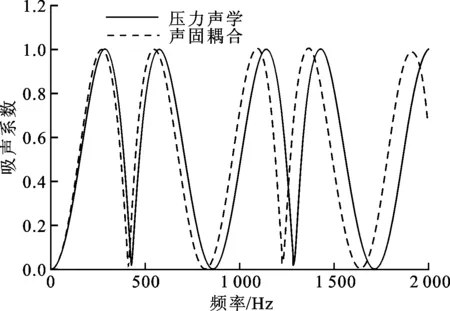
(a)系统吸声系数与频率的关系
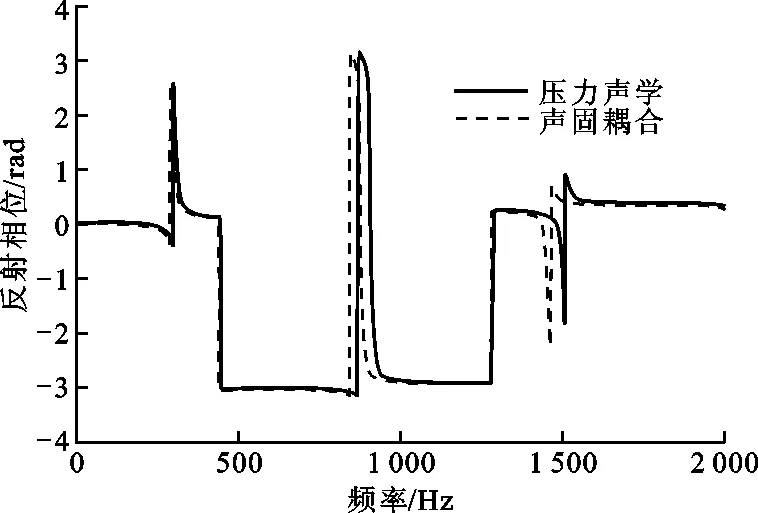
(b)系统反射相位与频率的关系图3 压力声学与声固耦合2种情况下系统吸声系数和反射相位随频率的变化曲线
2 参数对声学超表面吸声系数和反射相位的影响
如前所述,随着超表面在声学领域的应用越来越广泛,声学超表面结构的设计已经成为研究热点,而分析所设计模型的参数对声学超表面物理特性的影响,探究影响机理,对设计出更符合工程实际的声学超表面结构大有裨益。影响迷宫型声学超表面物理特性的因素很多,这一节主要研究本文所设计结构的主要参数——迷宫盖板上的小孔直径d、超表面原胞边长a、迷宫槽宽w、迷宫棱宽b和迷宫盖板厚度t的影响。
本文设计的亚波长迷宫型声学超表面原胞结构由一个穿孔盖板和一个正方迷宫构成,正方迷宫可以看作是一个折叠的赫姆霍兹共鸣器。赫姆霍兹共鸣器的共振频率[23]
(3)
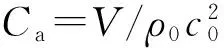
(4)
式中:l是赫姆霍兹共鸣器的空气管长度;V是迷宫内部空腔的体积。
本文模型的几何参数取值如下:h=10 mm,w=10 mm,a=60 mm,b=1.5 mm,d=3.8 mm,t=0.26 mm。空气密度为1.25 kg/m3,声速为343 m/s,动力黏度为17.9 μPa·s。迷宫材料为环氧树脂,迷宫盖板材料为不锈钢,具体材料参数见表1。为了便于发现和总结影响规律,在讨论特定参数时,其他参数取表2中的值。
2.1 迷宫盖板小孔直径的影响
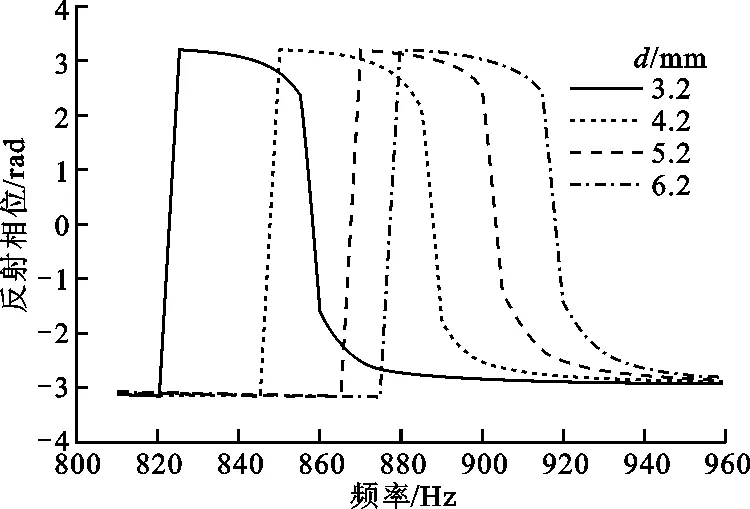
在其他参数不变的情况下,小孔直径d取不同的值,通过计算得到一组吸声系数和反射相位随频率的变化曲线,如图4所示。
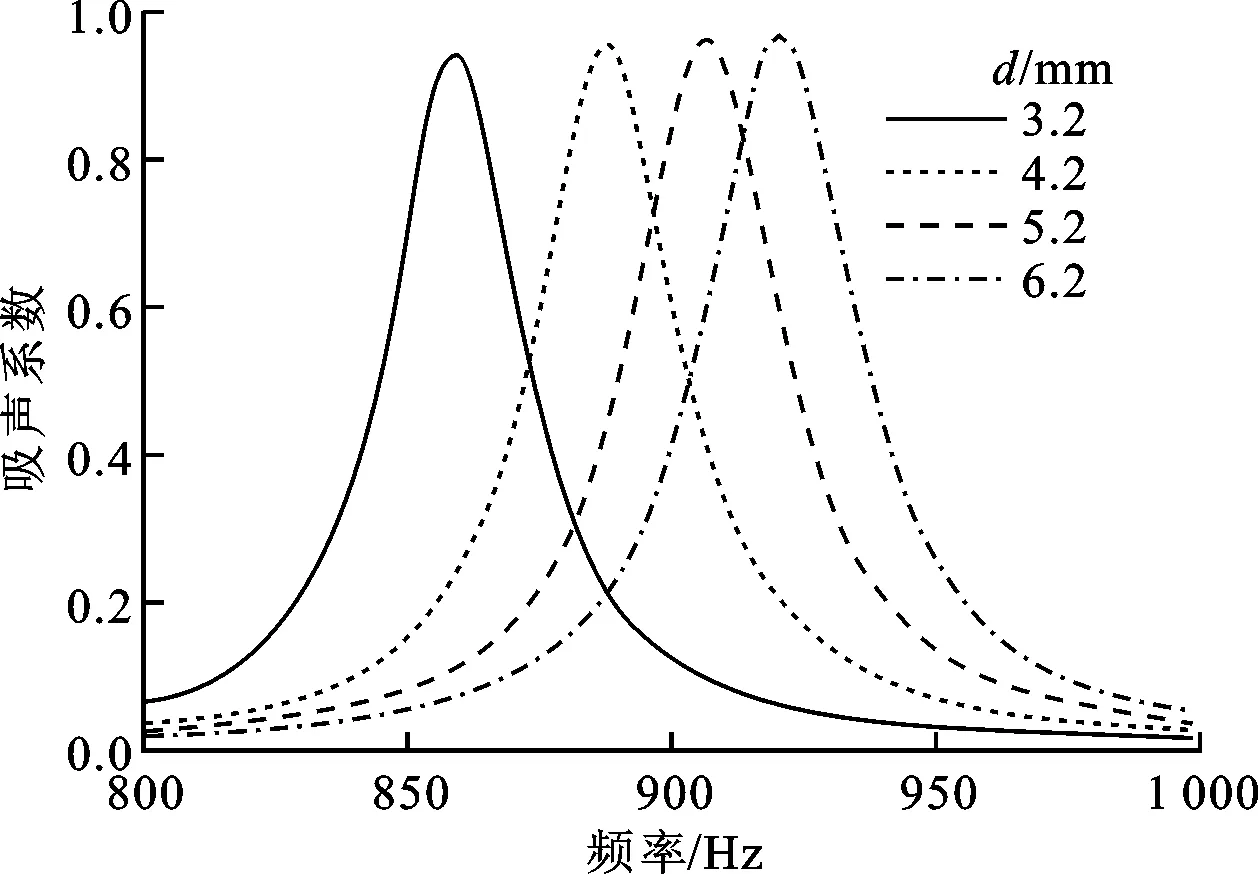
(a)小孔直径对吸声系数的影响
(b)小孔直径对反射相位的影响图4 小孔直径对声学超表面原胞吸声系数和反射相位的影响
从图4可以看出,小孔直径对系统的吸声系数和反射相位影响很大。由图4a可知,在800~1 000 Hz频段内,随着孔径变小,相应的共振频率降低,吸声系数曲线向低频移动但峰值保持不变。这主要是因为随小孔直径变小,相应的小孔横截面积也变小了,但迷宫空气腔的体积没有变,小孔长度也没有变,所以共振频率会向低频移动,这是由赫姆霍兹吸声的共振原理公式决定的;吸声系数峰值保持不变的原因主要是,小孔直径变小会使小孔内空气的黏性效应变大,从而使整个系统的声能量耗散更充分,但是小孔横截面积减小会增大声阻,而声阻影响声能量的耗散,所以总体上吸声系数峰值保持不变。
由图4b可知,在810~960 Hz频段内小孔直径对反射相位有很好的调节作用,随着孔径变小,反射相位曲线向低频移动但相位幅值保持不变。这主要是因为小孔直径减小使相应的小孔横截面积变小,但迷宫空气腔的体积没有变,小孔长度也没有变,所以共振频率会向低频移动;相位幅值保持不变的原因是小孔直径越小,小孔的黏性效应就越大,从而使声阻变大,但同时声抗也随之变大,所以相位幅值保持了同幅平移。
综上所述,小孔直径会影响小孔里空气的黏性,而空气黏性会影响声能量的耗散;小孔直径也会影响小孔的声阻和声抗,声阻和声抗又会影响系统的反射相位,并且声阻还会影响能量的耗散。
2.2 超表面原胞边长的影响
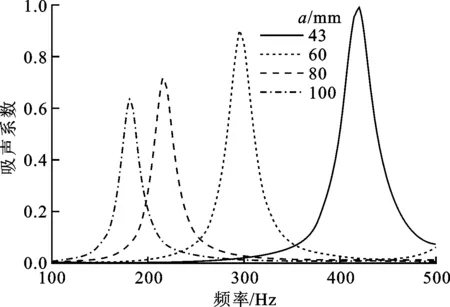
其他参数不变,超表面原胞边长a取不同值,通过计算得到一组吸声系数和反射相位随频率的变化曲线,如图5所示。
从图5可以看出,超表面原胞边长对元胞的吸声系数和反射相位影响很大。由图5a可知,在100~500 Hz频段内,随着超表面原胞边长变小,相应的共振频率向高频移动,吸声系数峰值逐渐变大。这主要是由于超表面原胞边长变小使原胞的面积变小,从而使声质量变小,相应地共振频率就会升高,这是由赫姆霍兹吸声的共振原理公式决定的。当超表面原胞边长很大时,迷宫内空气的黏性效应可以忽略不计,声能量在较宽的频段内可以充分耗散,而当超表面原胞边长很小时,不仅要考虑迷宫内空气的黏性效应,还要考虑迷宫内空气腔弥补实现阻抗匹配的小孔的黏性效应所引起的声阻抗,加之由于共振频率升高使散射波也增多等因素,所以吸声系数峰值变大,而部分峰值处声波没有达到完美吸收的原因是散射与耗散之间动态平衡的结果。
(a)超表面原胞边长对吸声系数的影响
(b)超表面原胞边长对反射相位的影响图5 超表面原胞边长对原胞吸声系数和反射相位的影响
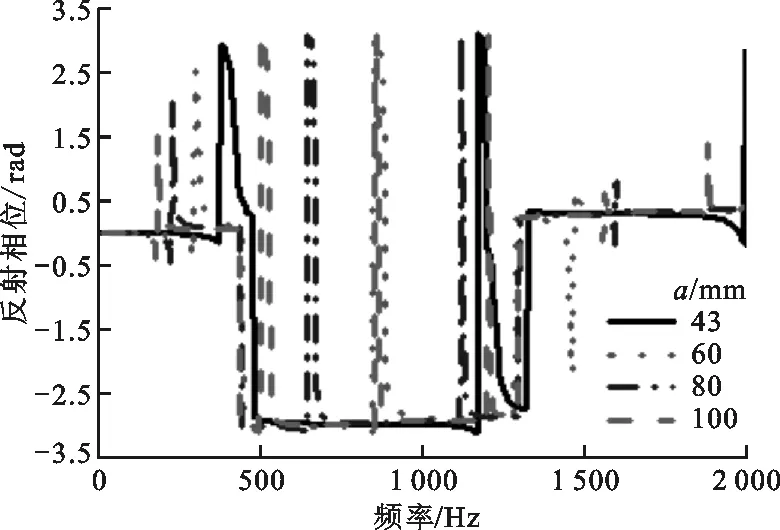
由图5b可知,在0~2 000 Hz频段内,超表面原胞边长对反射相位有很明显的调节作用,随着超表面原胞边长变小,反射相位曲线向高频移动,相位幅值基本不变但是跨度小幅增大。这主要是由于超表面原胞边长变小使原胞的面积减小,从而使声质量变小,而相应的共振频率则会提高,相位幅值基本保持不变但是跨度小幅增大;随超表面原胞边长减小,迷宫空气腔的横截面积变小,声抗增大,同时空气腔的气体黏性增大,声阻也随之增大。
2.3 迷宫槽宽的影响
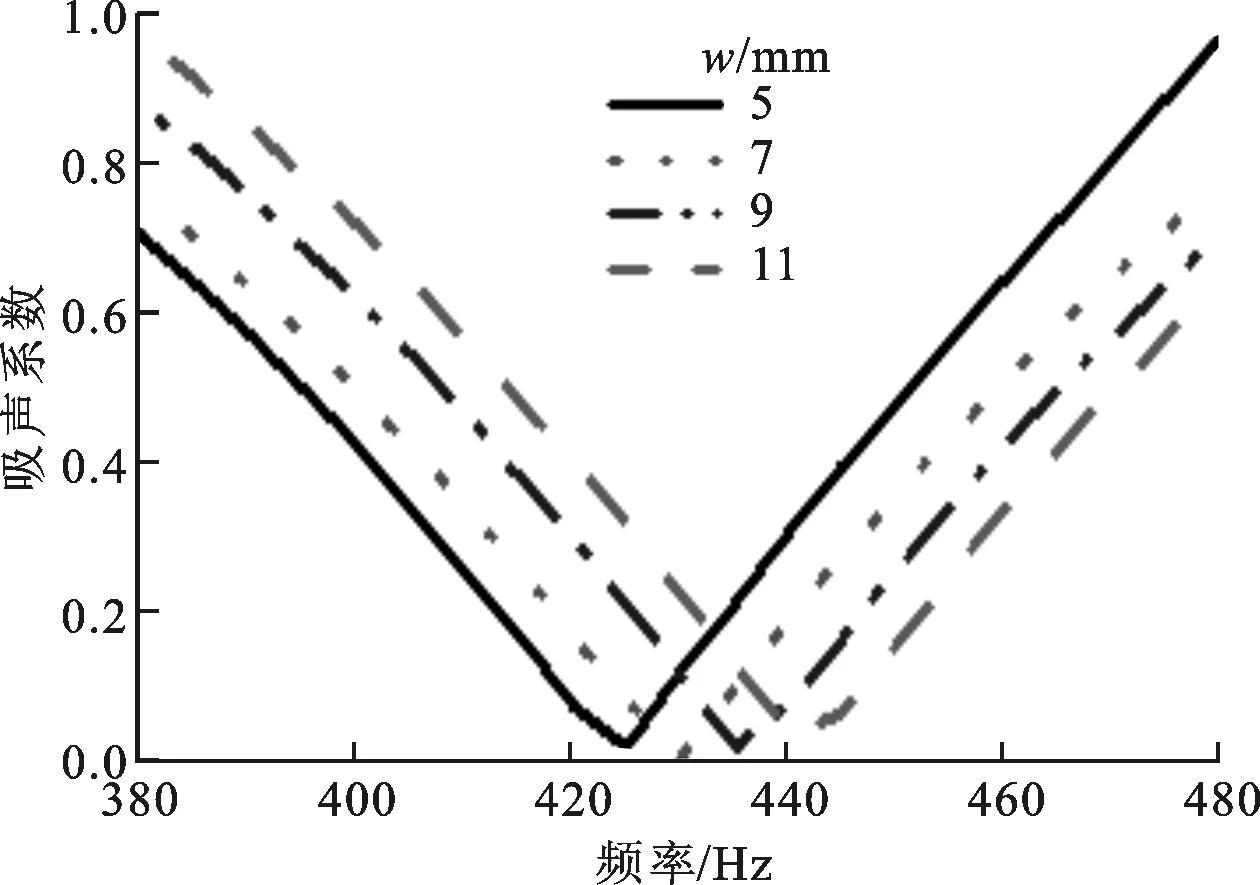
在其他参数不变的情况下,迷宫槽宽w取不同值,通过计算得到吸声系数和反射相位随频率的变化曲线,如图6所示。
从图6可以看出,迷宫槽宽对系统的吸声系数和反射相位有很大的影响。由图6a可知,在380~480 Hz频段内,随着迷宫槽宽变小,相应的共振频率向低频移动,吸声系数峰值变大。共振频率变低主要是由于迷宫槽宽减小使相应的空气腔面积变小,而吸声系数峰值变大主要是由于迷宫槽宽减小使迷宫空气腔的特性声抗及相应的有效长度leff变小所导致的。
(a)迷宫槽宽对吸声系数的影响
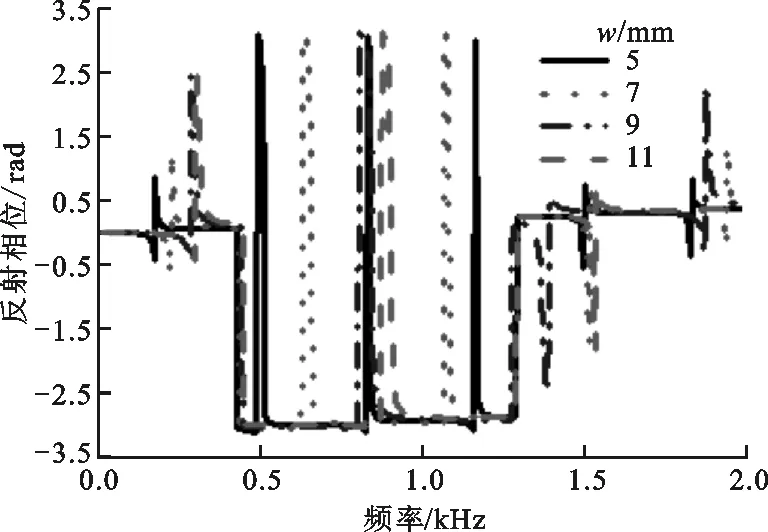
(b)迷宫槽宽对反射相位的影响图6 迷宫槽宽对声学超表面原胞吸声系数和反射相位的影响
由图6b可知,在0~2 000 Hz频段内迷宫槽宽对反射相位有很好的调节作用,随着迷宫槽宽的减小,反射相位曲线向低频移动,而相位幅值不变但跨度小幅减小。这主要是因为随迷宫槽宽减小,相应的空气腔有效长度leff变小,声抗变大,而且迷宫槽宽越小,迷宫内空气腔和迷宫盖板上小孔的空气黏性效应就越强,声能量耗散效果就越好,声阻也会变大,因此相位幅值保持不变而相位跨度变小。
2.4 迷宫棱宽的影响
在其他参数不变的情况下,迷宫棱宽b取不同值,通过计算得到吸声系数和反射相位随频率的变化曲线,如图7所示。
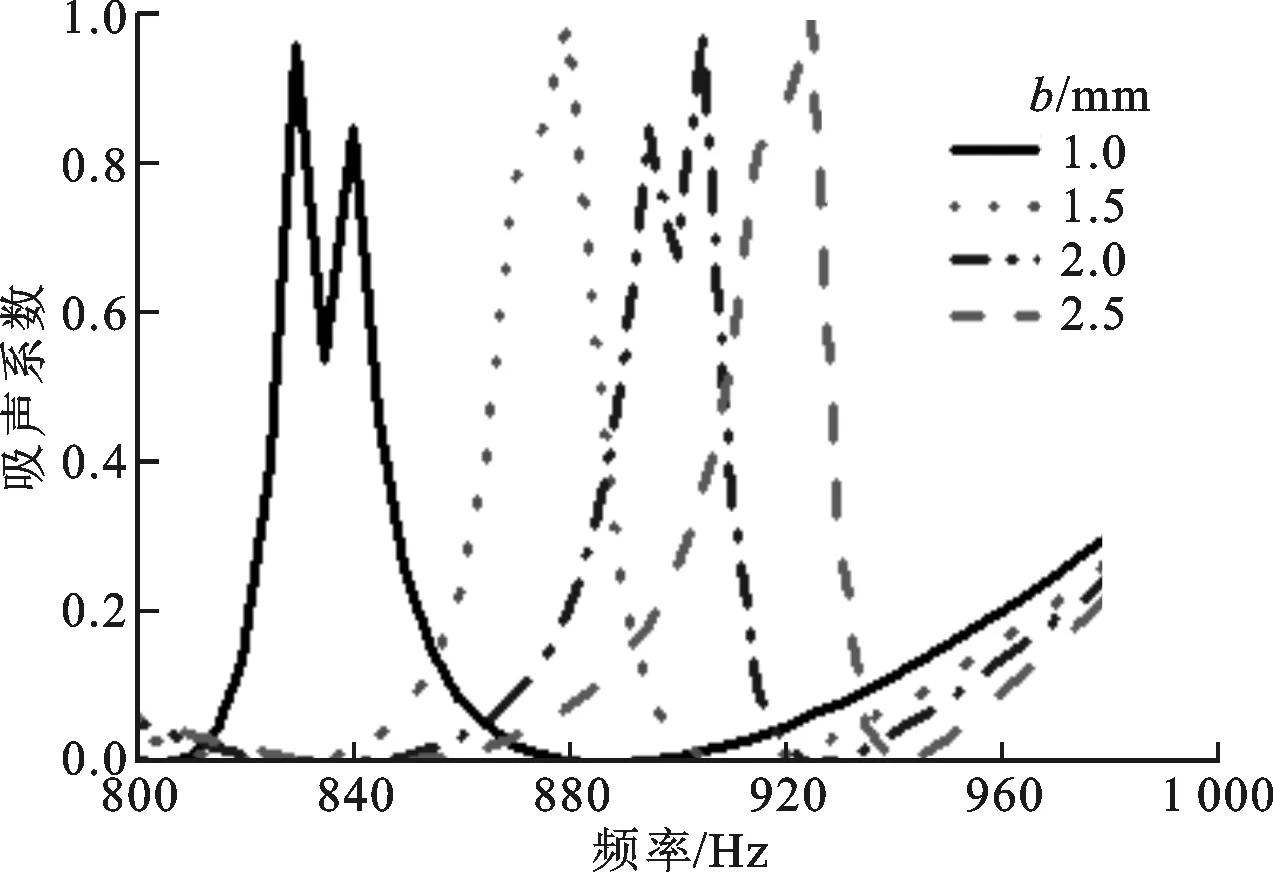
(a)迷宫棱宽对吸声系数的影响
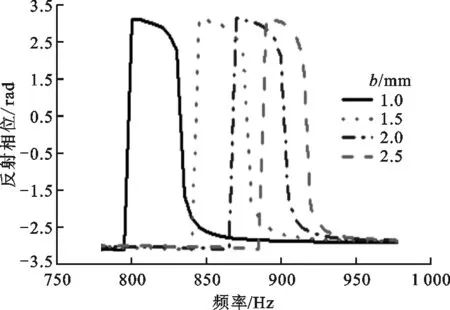
(b)迷宫棱宽对反射相位的影响图7 迷宫棱宽对声学超表面原胞吸声系数和反射相位的影响
从图7可以看出,迷宫棱宽对系统的吸声系数和反射相位有一定的影响。由图7a可知,在810~980 Hz频段内,随着迷宫棱宽变小,相应的吸声系数曲线向低频移动,但峰值几乎不变,同时还可发现,棱宽b为1.0和2.0 mm时的吸声系数峰值比1.5和2.5 mm时的峰值多了一个下落点。随迷宫棱宽变小相应的共振频率向低频移动,主要是因为迷宫棱宽变小使超表面原胞的空气腔体积增大,从而引起共振频率降低;吸声系数峰值几乎不变主要是因为虽然空气腔体积变大使空气的黏性效应变大,但同时声能量耗散效果改善,所以吸声系数峰值几乎不变;吸声系数峰值多了一个下落点,是由于当棱宽为1.0和2.0 mm时,超表面原胞空气腔体积变大所引起的空气黏性效应增强的程度不如空气腔有效长度leff减小所引起的声抗变大的程度所致。
由图7b可知,在780~980 Hz频段内,迷宫棱宽对反射相位有一定的调节作用,随着迷宫棱宽变小,反射相位曲线向低频移动,相位幅值几乎相等,但b为2.5 mm时的相位比b为1.0 mm时的相位滞后。随迷宫棱宽变小反射相位曲线向低频移动,主要是因为迷宫棱宽减小使声质量变大的缘故;相位幅值几乎相等且b为2.5 mm时的相位比b为1.0 mm时的滞后,主要原因是两者声抗与声阻的比值几乎相等,而b=2.5 mm时共振发生在高频区域。
2.5 迷宫盖板厚度的影响
在其他参数不变的情况下,迷宫盖板厚度t取不同值,通过计算得到吸声系数和反射相位随频率的变化曲线,如图8所示。

(a)盖板厚度对吸声系数的影响
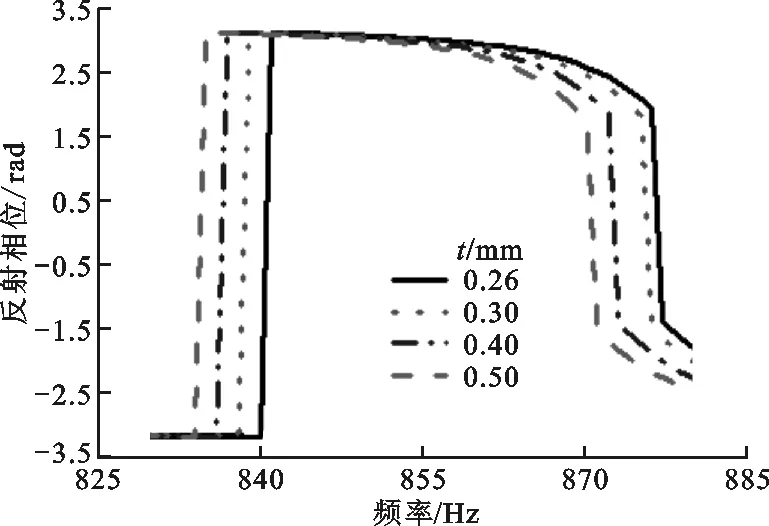
(b)盖板厚度对反射相位的影响图8 迷宫盖板厚度对声学超表面原胞吸声系数和反射相位的影响
从图8可以看出,迷宫盖板厚度对声学超表面原胞的吸声系数和反射相位有一定的影响。由图8a可知,在850~900 Hz频段内,随着迷宫盖板厚度变小,相应的吸声系数曲线向高频移动,但峰值几乎不变。这主要是由于随迷宫盖板厚度变小,盖板上小孔的厚度也变小,相当于亥姆霍兹共鸣器的管长变短,共振频率必然升高,而小孔厚度变小使小孔单位面积的黏性变大,吸声系数峰值本应该变大,但因为黏性效应的影响太小,所以吸声系数峰值几乎不变。
由图8b可知,在825~890 Hz频段内迷宫盖板厚度对反射相位有一定的调节作用,随着迷宫盖板厚度变小,反射相位曲线向高频移动,而且相位幅值保持不变。随着迷宫盖板厚度变小反射相位曲线向高频移动,主要是因为迷宫盖板厚度减小使盖板上小孔的厚度及小孔内空气的体积也变小,声质量亦随之变小,从而使共振频率提高;相位幅值保持不变是因为迷宫盖板厚度减小使盖板上小孔的厚度也变小,小孔内空气的黏性效应增强,导致声阻增大,但同时声抗也随之变大,所以相位幅值保持了同幅平移。
综上所述,通过调节迷宫盖板小孔直径、超表面原胞边长、迷宫槽宽和棱宽以及迷宫盖板厚度,都可以在一定频段内影响迷宫型超表面的吸声系数和反射相位,但相比之下,迷宫盖板小孔直径、超表面原胞边长和迷宫槽宽对系统的影响比较大,因此可以利用这3个参数方便地实现对吸声系数和反射相位的调节:通过控制吸声系数使声能量完全耗散,制作出迷宫型完美吸声器;通过控制反射相位使其在360°度内可以任意调控,制作出声隐身装置。考虑到操作的难易程度,通过改变超表面盖板上小孔的直径不失为一个简单而有效的办法,从这一点来看,本文的研究非常有意义。
3 结构设计及全相位调节
本文设计了一种具有10个沿着x轴正方向列阵的声学超表面原胞(如图1所示)的迷宫复合结构,10个原胞的其他参数均相同,只有孔的直径不同。这种结构虽然简单,却实现了从0到2π跨度上的相位调节。这种结构小巧紧凑,操作简单易行,还可以进一步拓展为由许多超表面原胞构造的超薄二维阵列平面,从而实现声隐身。
采用有限元软件COMSOL MultiphysicsTM4.3b中的声固耦合模块,对本文所设计的迷宫型复合结构的吸声系数、反射系数和相位进行计算。传播媒介为空气,平面波辐射边界条件加在入射声波的边界,平面波沿着z轴反方向入射,周期性边界条件加在y方向,以便于计算不同孔径时的反射波相位。复合结构的几何尺寸如下:h=10 mm,w=10 mm,a=60 mm,b=1.5 mm,t=0.26 mm,d=3.0,3.5,4.0,4.5,4.8,5.0,5.5,6.0,6.5,6.8 mm。空气密度取1.293 kg/m3,声速取343 m/s,动力黏度取17.9 μPa·s。迷宫材料为环氧树脂,盖板材料为不锈钢,材料参数见表2。计算结果如图9所示。
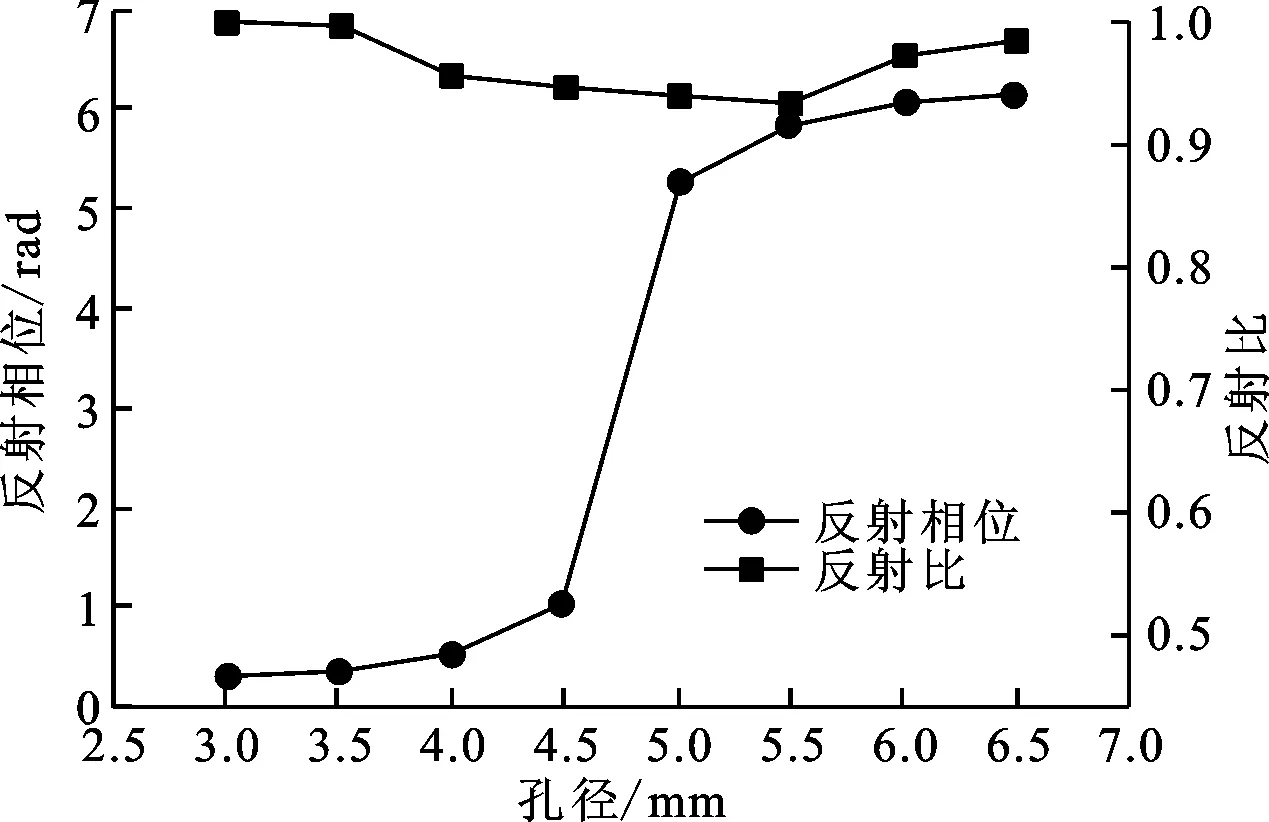
(a)反射相位和反射比随孔径的变化

(b)10个声学超表面原胞的反射波声压场云图图9 迷宫复合结构反射相位、反射比随孔径的变化曲线和10个声学超表面原胞的反射波声压场云图
从图9a可以看出,在本文所设计的迷宫复合结构中,仅仅改变1个一维几何参数——迷宫盖板小孔直径,就可以在频率为900 Hz时实现反射相位从0到2π的任意调控。因为工作频率900 Hz不是声学超表面迷宫复合结构的共振频率,所以可以有效地避免由共振引起的能量损失。这10个声学超表面原胞反射波的平均反射比高达93%,满足声学斗篷的条件[24],因此可为进一步设计声学斗篷提供依据。从图9b可以看出,10个声学超表面原胞的反射波声压场云图很直观地反映了同一时刻10个原胞的反射波从0到2π的相位调节。上述结果表明,这种通过改变小孔直径来调节迷宫复合结构反射相位的方法非常有效,操作简单易行,具有实际应用价值。
4 结 论
本文设计了一种亚波长迷宫型声学超表面结构,通过改变迷宫超表面盖板上的孔径来调节反射相位,与常见的通过改变周期单元的边长尺寸来调节相位的方法相比,结构紧凑,简单易行。从迷宫型声学超表面的研究实际出发,分析了各个结构参数与所建声学超表面结构的关系,重点分析了声学超表面对反射相位的调节作用,从而实现了对声学超表面反射相位的人工调控。研究结果表明:
(1)迷宫盖板上小孔的直径、超表面原胞边长和迷宫槽宽对吸声系数和反射相位有决定性的影响,相对而言,迷宫棱宽和迷宫盖板的厚度对吸声系数和反射相位影响较小;
(2)随迷宫盖板上的孔径减小,相应的共振频率降低,吸声系数峰值保持不变,反射相位曲线也向低频移动,但相位幅值保持不变;
(3)随超表面原胞边长减小,相应的共振频率升高,同时吸声系数峰值增大,反射相位曲线向高频移动,相位幅值基本不变但是跨度增大;
(4)随迷宫槽宽减小,共振频率向低频移动,吸声系数峰值随之小幅增大,反射相位曲线也向低频移动,相位幅值不变但是跨度减小。
本文的声学超表面设计方法实现了把庞大的结构缩小到深亚波长尺度。同时,对声学超表面进行了逆向设计,实现了反射相位从0到2π的任意调节。本文的研究可为声隐身和超薄声学棱镜的实现提供支持,具有工程应用价值。
参考文献:
[1] 倪旭, 张小柳, 卢明辉, 等. 声子晶体和声学超构材料 [J]. 物理, 2012, 41(10): 655-662.
NI Xu, ZHANG Xiaoliu, LU Minghui, et al. Phononic crystals and acoustic metamaterials [J]. Physics, 2012, 41(10): 655-662.
[2] 梁彬, 程建春. 声波的“漩涡”: 声学轨道角动量的产生、操控与应用 [J]. 物理, 2017, 46(10): 658-668.
LIANG Bin, CHENG Jianchun. Acoustic vortices: production, manipulation and application of acoustic orbital angular momentum [J]. Physics, 2017, 46(10): 658-668.
[3] 陈怀军, 赵文霞, 郝长春. 一种具有宽频效应的声学超构材料 [J]. 西北师范大学学报(自然科学版), 2015, 51(4): 26-30.
CHEN Huaijun, ZHAO Wenxia, HAO Changchun. A kind of acoustic metamaterial with broadband effect [J]. Journal of Northwest Normal University (Natural Science), 2015, 51(4): 26-30.
[4] 陈怀军, 赵文霞, 郝长春. 亥姆霍兹共振器孔径长度对声学超构材料性能的影响 [J]. 西安文理学院学报(自然科学版), 2015, 18(3): 55-66.
CHEN Huaijun, ZHAO Wenxia, HAO Changchun. Influence on aperture length of Helmholtz resonators on performance of acoustic metamaterials [J]. Journal of Xi’an University (Natural Science Edition), 2015, 18(3): 55-66.
[5] 程营, 吴大建, 刘晓峻. 表面声学超构材料中的非对称声传输研究 [J]. 声学技术, 2013, 32(6): 33-34.
CHENG Ying, WU Dajian, LIU Xiaojun. Asymmetrical transmission of sound wave in acoustic surface metamaterials [J]. Technical Acoustics, 2013, 32(6): 33-34.
[6] 江雪, 李勇, 梁彬, 等. 基于声学超表面的声波操控 [J]. 声学技术, 2015, 34(6): 17-19.
JIANG Xue, LI Yong, LIANG Bin, et al. The manipulation of the reflected and transmitted acoustic wave based on the subwavelength acoustic metasurfaces [J]. Technical Acoustics, 2015, 34(6): 17-19.
[7] LI Yong, LIANG Bin, GU Zhongming, et al. Reflected wavefront manipulation based on ultrathin planar acoustic metasurfaces [J]. Scientific Reports, 2013, 3: 2546.
[8] ZHAO Jiajun, LI Baowen, CHEN Zhining, et al. Manipulating acoustic wavefront by inhomogeneous impedance and steerable extraordinary reflection [J]. Scientific Reports, 2013, 3: 2537.
[9] ZHAO Jiajun, LI Baowen, CHEN Zhining, et al. Redirection of sound waves using acoustic metasurface [J]. Applied Physics Letters, 2013, 103(15): 151604.
[10] MA Guancong, YANG Min, YANG Zhiyong, et al. Acoustic double negativity with coupled-membrane metamaterial [C]∥Proceedings of Meeting on Acoustics. Montreal, Canada: The Acoustical Society of America, 2013: 065039.
[11] XIE Yangbo, WANG Wenqi, CHEN Huanyang, et al. Wavefront modulation and subwavelength diffractive acoustics with an acoustic metasurface [J]. Nature Communication, 2014, 5: 5553.
[12] YANG Yihao, WANG Huaping, YU Faxin, et al. A metasurface carpet cloak for electromagnetic, acoustic and waterwaves [J]. Scientific Reports, 2016, 6: 20219.
[13] ZHU Yifan, ZOU Xinye, LI Ruiqi, et al. Dispersionless manipulation of reflected acoustic wavefront by subwavelength corrugated surface [J]. Scientific Reports, 2015, 5: 10966.
[14] FAURE C, RICHOUX O, FÉLIX S, et al. Experiments on metasurface carpet cloaking for audible acoustics [J]. Applied Physics Letters, 2016, 108(6): 064103.
[15] LIANG Zixian, LI Jensen. Extreme acoustic metamaterial by coiling up space [J]. Physical Review Letters, 2012, 108(11): 114301.
[16] XIE Yangbo, POPA B I, ZIGONEANU L, et al. Measurement of a broadband negative index with space-coiling acoustic metamaterials [J]. Physical Review Letters, 2013, 110(17): 175501.
[17] LI Yong, LIANG Bin, ZOU Xinye, et al. Extraordinary acoustic transmission through ultrathin acoustic metamaterials by coiling up space [J]. Applied Physics Letters, 2013, 103(6): 063509.
[18] FRENZEL T, BREHM J D, BÜCKMANN T, et al. Three-dimensional labyrinthine acoustic metamaterials [J]. Applied Physics Letters, 2013, 103(6): 061907.
[19] CAI Xiaobing, GUO Qiuquan, HU Gengkai, et al. Ultrathin low-frequency sound absorbing panels based on coplanar spiral tubes or coplanar Helmholtz resonators [J]. Applied Physics Letters, 2014, 105(12): 121901.
[20] LI Jing, WU Jiuhui, GUAN Dong, et al. Multilayer-split-tube resonators with low-frequency band gaps in phononic crystals [J]. Journal of Applied Physics, 2014, 116(10): 103514.
[21] GUAN Dong, WU Jiuhui, HOU Mingming, et al. Application of a Helmholtz structure for low frequency noise reduction [J]. Noise Control Engineering Journal, 2015, 63(1): 20-35.
[22] LI Yong, ASSOUAR B M. Acoustic metasurface-based perfect absorber with deep subwavelength thickness [J]. Applied Physics Letters, 2016, 108(6): 063502.
[23] 杜功焕, 朱哲民, 龚秀芬. 声学基础 [M]. 3版. 南京: 南京大学出版社, 2012: 84-87.
[24] ZHAI Shilong, CHEN Huaijun, DING Changlin, et al. Ultrathin skin cloaks with metasurfaces for audible sound [J]. Journal of Physics: D Applied Physics, 2016, 49: 225302.
[本刊相关文献链接]
王亚洲,秦国良,包振忠,等.时空耦合谱元方法求解刚性圆柱体表面的声传播问题[J].2017,51(7):24-29.[doi:10.7652/xjtuxb201707004]
包振忠,秦国良,耿艳辉,等.谱元法应用于涡声传播问题的研究[J].2016,50(11):110-114.[doi:10.7652/xjtuxb201611 017]
楼京俊,李海峰,邹明松,等.低频桨-轴-壳体耦合振动声辐射机理研究[J].2016,50(11):144-149.[doi:10.7652/xjtuxb 201611022]
邵卫东,李军.计算气动声学中的伽辽金玻尔兹曼方法研究[J].2016,50(3):134-140.[doi:10.7652/xjtuxb201603021]
方源,章桐,陈霏霏,等.电动车动力总成噪声品质粒子群-向量机预测模型[J].2016,50(1):41-46.[doi:10.7652/xjtuxb 201601007]
侯明明,吴九汇,姜宁.旋转封闭薄壁球壳辐射噪声的多极展开方法[J].2014,48(7):102-108.[doi:10.7652/xjtuxb2014 07018]
沈承,辛锋先,金峰,等.对边简支加筋三明治板隔声性能研究[J].2011,45(7):22-29.[doi:10.7652/xjtuxb201107005]
张荣欣,秦国良.用切比雪夫谱元方法求解均匀流场中的声传播问题[J].2009,43(7):120-124.[doi:10.7652/xjtuxb 200907026]
朱昌允,秦国良,徐忠.谱元方法求解波动方程及影响其数值精度的相关因素[J].2008,42(1):56-59.[doi:10.7652/xjtuxb200801013]
