极限状态法在游乐设施结构设计上的应用

2018-05-15邓贵德沈功田宋伟科徐永生

中国特种设备安全 2018年4期

邓贵德沈功田张勇宋伟科徐永生

（中国特种设备检测研究院北京 100029）

目前，我国游乐设施的基础设计标准为GB 8408—2008 《游乐设施安全规范》。该标准规定游乐设施结构的设计计算应包括应力计算、刚度计算、疲劳强度计算、稳定性计算、抗倾覆计算、防侧滑计算等，其中应力计算采用单一安全系数的许用应力设计法，要求游乐设施零部件及焊缝承受的最大应力不超过材料抗拉强度与许用安全系数之比，对于重要的轴、销轴及重要焊缝，许用安全系数≥5；对于一般构件，许用安全系数≥3.5（脆性材料≥8）[1]。

上述许用安全系数不但较大于欧盟和美国游乐设施标准中规定的安全系数，也大于起重机械、压力容器等特种设备规范标准规定的对应安全系数。因此，我国目前的游乐设施普遍存在结构设计笨重的问题，这一方面直接增加了承载结构的材料消耗和自重，另一方面运动构件自重增大会导致游乐设施电机、传动、制动等系统的成本大大增加，并加大了游乐设施运行过程中的能源消耗和运营成本。

极限状态法是一种以概率理论为基础、以分项系数表达、不使结构超越某种规定极限状态的设计方法，在建筑、铁路、公路、港口、水利水电等工程结构设计方面逐渐取代了传统的许用应力设计法，近年来也陆续被欧盟、美国、澳大利亚等国外游乐设施标准采纳。本文介绍了极限状态法的基本概念和应用现状，并对2个国外主要游乐设施设计标准EN 13814：2004和ASTM F2291—17中采纳的极限状态法进行了分析和比较，着重对比了极限状态、载荷组合、抗力系数等内容，在此基础上提出了在中国游乐设施标准中引入极限状态设计法的建议，并指出了需要进一步开展研究的内容。

1 极限状态设计法

1.1 极限状态

根据ISO 2394：2015《结构可靠性通用准则》[2]、GB 50153—2008 《工程结构可靠性设计统一标准》[3]等标准，极限状态是指整个结构或者结构构件进入的某种特定状态，超过该状态后整个结构或结构构件就不再满足设计规定的某一功能要求。简而言之，极限状态就是区分结构或构件失效与否的临界状态。

结构极限状态分为承载能力极限状态和正常使用极限状态。承载能力极限状态对应于结构或构件达到最大承载力或进入不适于继续承载的变形状态，当结构或构件出现如下状态之一时，应认为超过了承载能力极限状态[3]：

1）结构构件或连接因超过材料强度而破坏，或因过度变形而不适于继续承载；

2）整个结构或其一部分作为刚体失去平衡；

3）结构转变为机动体系；

4）结构或其构件丧失稳定；

5）结构因局部破坏而发生连续倒塌；

6）地基丧失承载力而破坏；

7）结构或构件疲劳破坏。

正常使用极限状态对应于结构或构件达到正常使用或耐久性能的某项规定限值的状态，当结构或构件出现如下状态之一时，应认为超过了正常使用极限状态[3]：

1）影响正常使用或外观的变形；

2）影响正常使用或耐久性能的局部损伤；

3）影响正常使用的振动；

4）影响正常使用的其他特定状态。

结构设计时应对结构的不同极限状态分别进行计算，当某一极限状态的计算起控制作用时，可仅对该极限状态进行计算。

1.2 设计计算原理

结构的极限状态可用如下极限状态方程描述[3]：

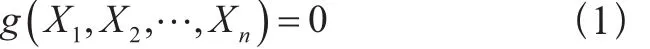
式中：

g(·)——结构的功能函数；

——基本变量，指作用在结构上的各种载荷和环境影响、材料性能参数、几何尺寸参数等。

结构按极限状态设计时应符合下式要求：

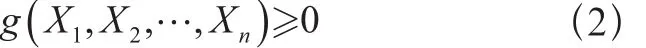
当采用结构的载荷效应和结构的抗力作为综合基本变量时，结构按照极限状态设计应符合下列要求：

式中：

R——结构的抗力，即结构承受载荷效应的能力；

S——载荷或载荷组合在结构中产生的效应，广义的载荷效应包括结构应力、应变、挠度、转角、内力、力矩或者其他极限状态控制值，狭义的载荷效应可以选定为应力。

结构抗力通常是所用材料力学性能和结构几何参数的函数，载荷效应则与结构可能承受的各种载荷特性有关。R和S都是与基本变量相关的随机变量，因此Z也是一个随机变量，随机变量Z以某一概率的形式满足式（3）的要求，这个概率值就是结构的可靠度，与之相对的则是结构的失效概率。

1.3 结构可靠度与失效概率

结构可靠度是度量结构可靠度的指标，定义为结构在规定的时间内和规定的条件下，完成预定功能的概率。与之相对，失效概率则是指结构不能完成预定功能的概率。

失效概率Pf表达式如下：

式中：

fR(r)——结构抗力的概率密度函数；

fS(s)——载荷效应的概率密度函数。

根据失效概率Pf，可以计算结构可靠度Pre：

除了结构可靠度Pre外，可靠指标β也常用于衡量结构的可靠性，可靠指标与可靠度和失效概率的关系如下：

式中：

Φ−1(·)——标准正态分布函数的反函数。

当抗力R和载荷效应S都为服从正态分布的随机变量且相互独立时，可靠指标β有如下表达式[4]：

式中：

μR、μS——结构抗力和载荷效应的平均值；

σR、σS——结构抗力和载荷效应的标准差。

1.4 载荷组合

载荷按照随时间的变化，可以分为永久载荷、可变载荷和偶然载荷。永久载荷如结构自重，随时间变化很小，通常可按照随机变量进行统计分析。可变载荷如风载荷、雪载荷和乘员活载荷等，载荷随时间变化量大，属于随机过程，但是考虑到随机过程处理复杂，通常采用简化的随机过程概率模型描述，即将设计基准期内载荷的标准值作为随机变量代替随机过程来进行统计分析。偶然载荷如地震载荷、爆炸载荷等，在结构设计使用年限内不一定出现，一旦出现其量值很大但持续时间很短。偶然载荷按照可能出现的最大值确定设计值，如地震载荷可按照地震载荷的重现期确定设计值[3]。

当结构承受两种或两种以上的可变载荷作用时或者可变载荷和偶然载荷作用时，考虑到这些载荷同时出现最大值的概率很小，通常可以对起主导作用外的伴随可变载荷乘以小于1的组合系数，折减后进行载荷组合。

在进行承载能力极限状态设计时，通常需要考虑基本组合和偶然组合两种载荷组合工况，其中基本组合适用于结构使用过程中一定出现且持续期很长的设计状况，以及施工和使用过程中出现概率较大但持续期很短的设计状况；偶然组合适用于结构使用过程中出现概率很小且持续期很短的设计工况，两种载荷组合形式见式（8）和式（9)；在进行正常使用极限状态设计时，可根据不同情况采用载荷的标准组合、频遇组合或准永久组合，组合形式分别见式（10）～式（12)[3]。

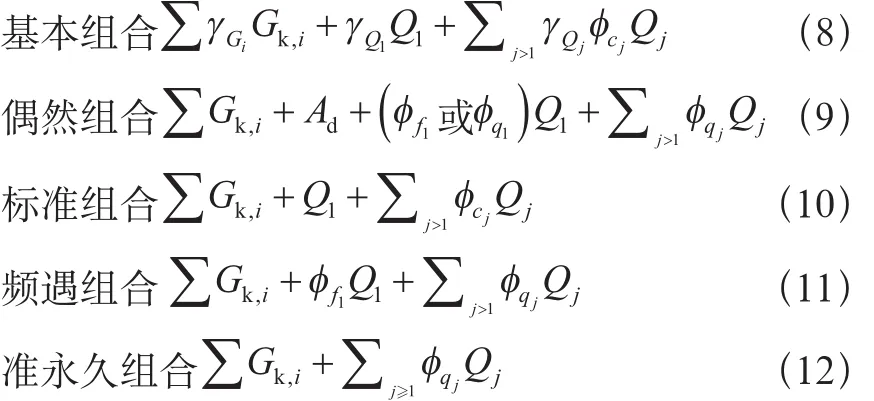
式中：

Ad——偶然载荷的设计值；

Gk,i——第i个永久载荷标准值；

Q1——第1个可变载荷（主导可变载荷）标准值；

Qj——第j个可变载荷标准值；

γGi——永久载荷分项系数；

γQ1——第1个可变载荷分项系数；

γQj——第j个可变载荷分项系数；

φcj——第j个可变载荷的组合值系数；

φf1——第1个可变载荷的频遇值系数；

φq1——第1个可变载荷的准永久值系数；

φqj——第j个可变载荷的准永久值系数。

需要指出的是，上述载荷组合表达式中符号“∑”和“+”均表示组合，即同时考虑所有载荷对结构的共同影响，而不表示代数相加。

1.5 分项系数

极限状态法被认为是一种先进的结构设计方法，但是直接采用1.3节介绍的可靠度方法进行结构设计需要概率和数理统计学基础且涉及概率运算，对于大多数设计人员来说应用存在困难。为此，国内外研究人员通过人为引入分离函数的方式将可靠指标分解换算，表达成设计人员习惯采用的分项安全系数，使极限状态设计法与传统单安全系数设计方法形式相近，这样既内含了结构可靠性设计基本要求，又不直接涉及统计参数、概率模型和概率计算，便于工程实际应用。

式（13）是一种典型的采用分项系数表示的承载能力极限状态设计表达式[3]：

式中：

Rd——抗力设计值；

Sd——载荷组合效应值；

γ0——结构的重要性系数；

γM——抗力分项系数；

σM——材料力学性能标准值。

式（13）中包含的抗力分项系数γM，以及式（8）～式（12）中的载荷分项系数γGi、γQ1、γQj、φcj、φf1、φq1和φqj，由标准规范的研制人员根据结构承受载荷、所用材料以及几何尺寸等各变量的概率模型、统计特性，在规定的失效概率或者目标可靠指标条件下，按照结构可靠度方法针对有代表性的典型结构计算分析得到。如果未给出具体的目标可靠度，则宜用校准法对按传统许用应力法设计的已有结构进行反演计算，求得已有结构可靠指标，并经综合分析判断决定。

1.6 应用现状

目前，欧盟境内所有的建筑和土木工程结构设计均采用基于《欧洲结构规范》的极限状态设计法，以消除妨碍欧盟成员国市场自由的技术壁垒，并确保欧盟境内的工程结构具有一致的安全可靠性[5]。欧洲起重机械标准规定的首选设计校核方法为极限状态法，但是对于载荷和载荷效应成线性关系的MDC1级起重机械可以采用许用应力法[6]。美国公路桥梁设计规范从20世纪80年代后期引入了基于结构可靠性和极限状态设计理论的载荷抗力系数法（LRFD），1994年至2006年与许用应力法并行使用，2007年后完全采用极限状态法设计规范[7]。

目前，我国房屋建筑、铁路、公路、港口、水利水电等工程结构设计均已引入极限状态设计方法。为了统一这些工程结构设计的基本原则、要求和方法，我国制定颁布了《工程结构可靠性设计统一标准》，规定工程结构设计宜采用以概率理论为基础、以分项系数表达的极限状态设计方法，当缺乏统计资料时也可采用容许应力或单一安全系数等经验方法[3]。我国的《起重机设计规范》规定起重机结构设计计算可采用许用应力设计法或极限状态设计法，当结构在外载荷作用下产生了较大变形，以致内力与载荷呈非线性关系时，宜采用极限状态设计法[8]。

2 欧美游乐设施设计标准比较

EN 13814：2004 《游乐场所机械和结构安全》[9]、ASTM F2291—17 《游艺机和游乐设施设计标准惯例》[10]是欧盟和美国现行最新的游乐设施设计标准。这两个标准均引入了极限状态设计方法用于游乐设施结构设计，其中EN 13814：2004只规定了极限状态设计法，ASTM F2291—17规定可以采用许用应力法或载荷抗力系数法，其中载荷抗力系数法实质就是一种以分项系数表达的极限状态设计法。

2.1 针对的极限状态

EN 13814: 2004在第5.1.4条明确规定，设计验算应当包括承载能力极限状态，疲劳极限状态，屈曲极限状态，变形极限状态（必要时），抗倾覆、抗滑移和抗提升安全验证以及动态分析。参照GB 50153—2008对于承载能力极限状态的规定，疲劳、屈曲、抗倾覆、抗滑移和抗提升以及过度变形均属于承载能力极限状态，因此可以进一步归纳认为，EN 13814：2004针对的极限状态主要是承载能力极限状态，以防止结构出现静强度失效、疲劳失效、稳定性失效、过度变形等失效模式。

ASTM F2291—17的设计部分规定，设计人员应当分析校核结构不会出现显著塑性变形或者垮塌，应当采用强度和疲劳两个准则来评价应力结果；对于移动式游乐设施，还规定要确保其不会发生倾覆；如果结构部件或者结构整体变形对结构正常运行有影响时，还应当进行变形分析。同样，参照GB 50153—2008的规定，ASTM F2291—17针对的极限状态有承载能力极限状态和正常使用极限状态，承载能力极限状态校验主要是防止静强度失效、疲劳失效、稳定性失效等失效模式，正常使用极限状态是防止出现影响正常工作的变形。

2.2 规定的载荷组合

●2.2.1 EN 13814: 2004

EN 13814: 2004第5章要求游乐设施承载结构极限状态应当考虑基本组合、偶然组合和疲劳组合三种载荷组合，其中基本组合中包括2种载荷组合。标准给出了基本组合和偶然组合的表达式，规定了疲劳组合需要考虑的载荷但未给出表达式。

基本组合1：

基本组合2：

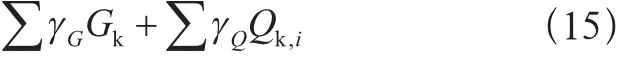
式中：

γG——永久载荷分项系数，式（14）中取1.35，

式（15）中取1.1；

γQ——可变载荷分项系数，1.35；

Gk——永久载荷标准值；

Qk,i——第i个可变载荷标准值。偶然组合：

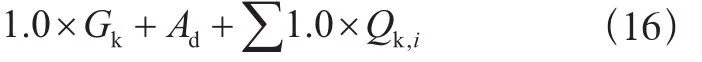
式中：

Ad——偶然载荷的设计值。

偶然载荷，例如地震载荷，只在有特殊要求时才需考虑。考虑偶然载荷时，采用式（16）所示组合，但考虑地震载荷时不需要同时考虑风载荷。

EN 13814: 2004规定，在进行结构疲劳分析时应当考虑作用位置变化的永久载荷、移动的外加载荷、驱动力和制动力、冲击和振动载荷、预设碰撞力、离心力、科氏力等载荷，但是无须考虑雪载荷、温度载荷、装配载荷、不改变作用位置的永久载荷、不产生振动的风载荷，以及可变载荷中不随时间和位置变化的分量；对于疲劳载荷产生的、组成疲劳设计应力谱的每一个应力分量的波动范围，应乘以一个不小于1的疲劳载荷分项系数γFf，应力分量波动范围之间不再施加组合系数；在疲劳强度校核部分，标准明确规定γFf取1.0。

在整体结构稳定性方面，EN 13814: 2004给出了防止倾覆、侧滑和提升的设计表达式和分项安全系数。

防止倾覆：

防止侧滑（无地脚螺栓）：

防止侧滑（有地脚螺栓）：

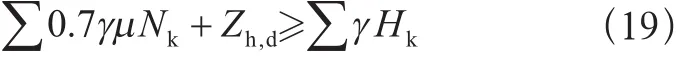
防止提升（无地脚螺栓）：

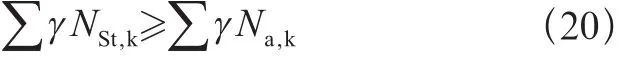
防止提升（有地脚螺栓）：

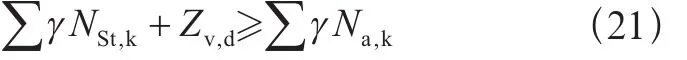
式中：

Hk——水平载荷分量；

Nk——垂直载荷分量；

Na,k——垂直提升载荷；

NSt,k——垂直稳定载荷；

MK,k——倾覆力矩；

MSt,k——稳定力矩；

Zh,d——地脚螺栓的水平承载能力；

Zv,d——地脚螺栓的垂直承载能力；

μ——摩擦系数；

γ——分项安全系数，见表1。

表1 稳定性分析分项安全系数

●2.2.2 ASTM F2291—17

ASTM F2291—17没有明确给出极限状态法的载荷组合公式，设计人员可以参考游乐设施使用地认可的、现行国家建筑标准中的载荷组合公式，这些标准包括但不限于：《国际建筑规范》第16章“结构设计”、ANSI/ AISC 360—05 《美国钢结构设计规范》、ASCE/SEI 7—05 《美国建筑载荷设计规范》、《加拿大建筑规范》、《欧洲结构规范》等。如果当地没有认可的国家建筑规范，载荷组合按照ASCE/ SEI 7—05《美国建筑载荷设计规范》。

下面以ASCE/SEI 7—05 《美国建筑载荷设计规范》为例，介绍其载荷组合。该规范第2章规定了7种基本载荷组合[11]。

基本组合1：

基本组合2：

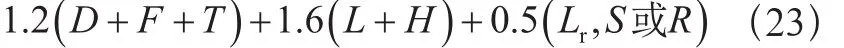
基本组合3：

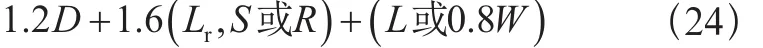
基本组合4：

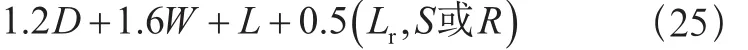
基本组合5：

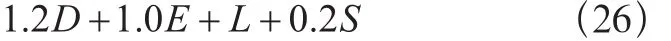
基本组合6：

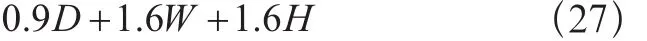
基本组合7：

式中：

D——永久载荷；

E——地震载荷；

F——流体压力和液柱静压力载荷；

H——侧向土、地下水或散装物料压力载荷；

L——活载荷（指乘员或用户载荷）；

Lr——屋顶活载荷；

R——雨载荷；

S——雪载荷；

T——温度载荷；

W——风载荷。

除了上述7种基本组合外，ASCE/SEI 7—05 《美国建筑载荷设计规范》还规定了包含洪水载荷的载荷组合和包含环境冰载荷的载荷组合。

当结构位于洪水高危区域时，应采用1.6W+2.0Fa代替式（25）和式（27）中的1.6W；当结构位于洪水区域但非高危区域时，应采用0.8W+1.0Fa代替式（25）和式（27）中的1.6W，其中Fa为洪水载荷。

当结构承受环境冰载荷时，应采用0.2Di+0.5S代替式（23）中的0.5(Lr，S或R)，采用Di+Wi+0.5S代替式（25）中的 1.6W+0.5(Lr，S 或 R)，采用 Di+Wi代替式（27）中的1.6W，其中Di为冰载荷、Wi为考虑结构裹冰后的风载荷。

疲劳分析时，应当考虑可能产生最大应力、应变波动范围的载荷组合形式；除动载荷冲击系数不小于1.2外，对所有其他疲劳载荷施加1.0的载荷分项系数。该标准明确指出采用1.0的载荷分项系数是因为疲劳相关载荷都是取预计可能出现的最大值，并且疲劳许用应力值不是平均值或者典型值，而是平均值减去2倍标准差后的设计值。

对于稳定性分析，ASTM F2291—17仅原则规定移动式游乐设施在安装和运行时应能保持稳定、防止倾覆，并且需要考虑所有最不利的工况，例如不平衡载荷、风载荷等。但是，标准未对固定式游乐设施的稳定性提出要求，也未规定移动式游乐设施稳定性分析的设计表达式和安全系数。

2.3 规定的抗力系数

●2.3.1 EN 13814: 2004

对于静强度，EN 13814: 2004强度校核部分规定，钢制机械部件的抗力设计值应当满足：

式中：

fy——标准规定的材料屈服强度；

fu——标准规定的材料抗拉强度；

γMy——抗力分项系数（屈服强度），取1.1；

γMu——抗力分项系数（抗拉强度），取1.35。

材料抗力设计值采用两式中的较小者。对于横向力和扭矩产生的剪切应力，材料抗力设计值还应当乘以α=0.58的系数。

对于疲劳强度，EN 13814: 2004强度校核部分规定，钢材的疲劳抗力分项系数应根据断裂后果和定期检验难度，按表2取值。

表2 疲劳抗力分项系数

●2.3.2 ASTM F2291—17

ASTM F2291—17并未明确给出材料静强度抗力系数的值，只是规定可以从合适的载荷抗力系数法参考文献中选取材料抗力系数和名义强度。如果按照美国钢结构协会的《载荷和抗力系数设计规范》[12]，抗拉钢结构的抗力设计值等于0.9倍屈服强度或者0.75倍抗拉强度，相当于屈服强度抗力分项系数取1.11、抗拉强度抗力分项系数取1.33；对于抗弯钢梁，按照屈曲极限状态设计，屈服强度抗力分项系数也为1.11。

关于钢材疲劳强度，ASTM F2291—17规定可以直接采用美国焊接学会或者其他被美国认可标准中的疲劳强度数据，这些数据中已经包含了疲劳抗力安全系数。但是，对于其他基于平均值的疲劳数据，使用前应当进行修正，例如采用疲劳应力平均值减去2倍标准差的方法调整可以将疲劳失效概率降低至2.3%。

2.4 标准比对

ASTM F2291—17规定可以采用极限状态设计法或者许用应力法，两种方法并行可用，具体选择哪种方法由用户决定；标准未明确规定载荷组合公式、设计分项系数等设计所需关键信息；引用的相关设计标准范围很广，选用不同引用标准设计的结构难以保证具有一致的安全可靠度。上述情况可能与ASTM标准属性有关，ASTM标准实质上是自愿性团体标准[13]，本身不具备强制力，因此标准中保留了多种方法和并行选项，具体选择由标准用户决定，只要保证设备安全即可。

EN 13814: 2004只允许采用极限状态设计法，并明确给出了载荷组合公式、载荷分项系数和抗力分项系数等关键设计信息，这样可以保证设计出来的游乐设施具有尽可能一致的安全可靠度。原因一方面很可能是由于EN标准的主要目标就是致力于消除欧盟境内贸易技术障碍以构建统一市场，另一可能的原因是欧洲建筑、土木等工程结构行业均已经强制采用极限状态法，极限状态法在欧洲已有很好的应用基础和接受程度。总体上来说，EN 13814: 2004标准在极限状态法方面更加系统和明确，并且有《欧洲结构规范》作为强有力的技术支撑。

3 建议和意见

鉴于目前欧洲和美国两大国际主要游乐设施标准以及国内建筑、钢结构、起重机械等工程结构设计标准均已采纳引入了极限状态设计方法，我国应当加快开展基于极限状态法的游乐设施设计计算方法研究，建立典型游乐设施承载结构的极限状态设计计算方法并应用示范，在此基础上推动中国游乐设施标准中引入极限状态设计法，为设计建造安全轻量、节材节能的游乐设施提供重要技术支撑。

为了建立基于极限状态法的游乐设施设计计算方法，有以下工作需要进一步开展研究：

1）消化吸收国内外已有极限状态设计方法，掌握极限状态法的理论基础和前提假设，特别是要弄清基本随机变量的概率分布类型和特性、目标失效概率等用于确定分项安全系数的关键依据。

2）开展我国游乐设施主要载荷和典型材料性能的数据收集、试验测试和统计分析，确定主要载荷参数和典型材料性能参数的概率分布类型和统计特征值，提出规范设计值。

3）开展我国游乐设施极限状态设计计算模型研究，确定游乐设施承载极限状态和正常使用极限状态设计表达式，基于目标可靠指标提出游乐设施极限设计分项系数。

4）开展游乐设施极限状态设计法应用示范，通过数值仿真、试验测试等方法综合验证设计安全性。

上述研究工作中如何科学合理确定游乐设施复杂动态载荷的概率分布和统计特征值，进而确定合适的分项安全系数将会是游乐设施极限状态设计方法研究的难点，需要重点研究。

参考文献

[1]GB 8408—2008 游乐设施安全规范[S]．

[2]ISO 2394： 2015 General principles on reliability for structures[S]．

[3]GB 50153—2008 工程结构可靠性设计统一标准[S]．

[4]武清玺．结构可靠度、理论、方法及应用[M]．北京：科学出版社，2014：39-44．

[5]European Commission．Time line[EB/OL]．http：//eurocodes．jrc．ec．europa．eu/showpage．php?id=12．