超空泡航行体的扰动观测器补偿设计
2018-05-14庞爱平何朕
庞爱平 何朕
摘 要:针对水下高速超空泡航行体尾部与空泡壁周期性碰撞的现象,提出了采用扰动观测器来补偿和消除重力的影响。推导了扰动观测器方程,给出了补偿器设计方案。仿真验证了扰动补偿能够避免超空泡航行体前进中周期性碰撞空泡壁的现象,并且控制面偏转角满足正常工作范围的要求。接入扰动估计和补偿控制后,航行体由原来的周期性拍打空泡壁能很快恢复到平稳工作状态。结论是扰动观测补偿的设计能够避免超空泡航行体产生滑行,使运动更为平稳,并且减少了前进的阻力。所提的扰动估计和补偿的控制思想,避免了直接补偿时执行机构行程过大的问题,可用于一般的控制系统设计。
关键词:超空泡;超空泡航行体;扰动观测器;补偿;滑行
中图分类号:TP 273
文献标志码:A
文章编号:1007-449X(2018)01-0107-07
0 引 言
水下航行体因受到水的阻力作用而极大限制了其速度。超空泡技术的应用突破了水下航行体速度的瓶颈,提高了水下武器的战斗力,具有重大的科研意义和军事应用前景[1]。已成为国内外学者关注的热点[2-4]。
超空泡航行体的流体动力特性极其复杂,俄罗斯和乌克兰首先对超空泡航行体的建模与控制开展研究。乌克兰学者Savchenko[5]首先研究了航行体与空泡的作用关系,仿真分析超空泡航行体的开环运动,在开环状态下,航行体无法维持运动,必须采用主动控制来保证航行体的运动稳定。Kirschner等[6]提出可以采用尾翼和空化器作为控制面来联合控制航行体的运动稳定性,设计了LQR前馈反馈控制,可以维持航行体的运动稳定性。俄罗斯学者Dzielski等[7]在研究中提出了一种超空泡航行体的标准设计,建立了超空泡航行体的基准模型并给定相应参数,该模型既相对简化,又保留了超空泡航行体的基本特性,被之后的研究者所广泛采用[7-9]。Dzielski在文献[7]中还给出了一个线性状态反馈控制律,在这个控制律的作用下,航行体尾部周期性地拍打着空泡下壁高速前行。在Dzielski的研究基础上,Lin等在文献[9]中讨论了反馈增益对航行体极限环振荡的影响。
由于航行体被空泡包裹,失去水的浮力作用,在重力的作用下自然下沉,当尾部接触并刺穿空泡壁时产生反弹的滑行力,所产生的滑行力又将航行体推回空泡内,航行体受到重力作用再次下沉而与空泡壁再次碰撞,如此反复形成周期性的滑水现象。虽然这种周期性滑水的极限环稳态运行模式也是超空泡航行体一种典型的工作模式,但由于空泡的内径有限,当滑行力这个扰动外力过大时,会将航行体推向空泡的另一侧,来回冲撞导致航行体最终失去稳定,这就要求控制设计具有良好的抗扰动能力。此外航行体与空泡壁频繁的碰撞也产生阻力,消耗能量,不但影响前进速度,还有可能破坏空泡的稳定性,故良好的工作状态应该是避免滑行力的产生,消除这种周期性滑水现象。为了消除重力的影响,文献[7]和文献[9]中都采用反馈线性化或直接对消的方法设计了避免滑行力产生的控制方案,但是其设计的结果所要求的控制面偏转角过大,达到了1.5 rad,显然超出了正常的工作范围,因而无法得到实际应用。此外反馈线性化还要求精确的数学模型,这在实际中也是难于实现的。
这里需要指出的是,对于超空泡航行体来说,需要补偿的并不仅仅是简单的一个重力,还包含其轨迹控制中的航迹变化问题,需要补偿的是一个未知的常值扰动。本文分析了超空泡航行体的常值扰动,采用扰动观测器的方法对这个常值扰动进行估计和补偿[10]。文中推导了扰动观测器算法,设计了基于扰动观测和补偿的超空泡航行体反馈控制方案, 避免了超空泡航行体的周期性滑水现象,无需加大执行机构的行程,且具有一定的鲁棒性。
1 超空泡航行体动力学模型
本文采用文献[7]中给出的超空泡航行体的基准模型和参数。超空泡航行体的示意图如图1所示,其整体为长度比为1:2的梭形,總长度为L0,半径为R,与水的密度比为m。超空泡航行体的头部与空化器相连,空化器除了产生和维持空泡,还能偏转一定的角度而产生流体动力,空化器和尾翼共同控制航行体的运动稳定。
3 仿真验证
为了说明反馈控制器(20)在加上扰动观测器后的补偿效果,下面分3种情况进行验证说明。第1种情况是在航行体初始下沉速度w(0)=1,这种情况是文献[7]和文献[9]为了避免产生滑行而给出的典型算例,最终都以δc超出实际可能值而放弃了这个方案,而在本文设计的扰动补偿下,δc完全可以在正常工作范围内消除滑行。第2种情况是航行体在反馈控制作用下典型的拍打着滑水前进的情况,在接上扰动观测器并进行补偿后,航行体很快就平稳了下来。第3种情况则是航行体按照航迹要求航行的例子,可以看到,估计器随航迹要求的xeq给出不同的扰动估计值。这3种情况都表明补偿后航行体能平稳运行,不再产生滑水的拍打现象。
第1种情况:初始速度w(0)=1,航迹输入xeq=0。各个状态变量的响应曲线如图5所示, 对应的控制输入及滑行力如图6所示,观测器输出如图7所示。从图中可见,航行体仅与空泡壁碰撞1次,经过1个波的振荡后就逐渐收敛到平衡点,相应的控制偏转角均小于0.2 rad。约0.4 s后观测器输出趋于稳定值,航行体恢复稳定运行状态。
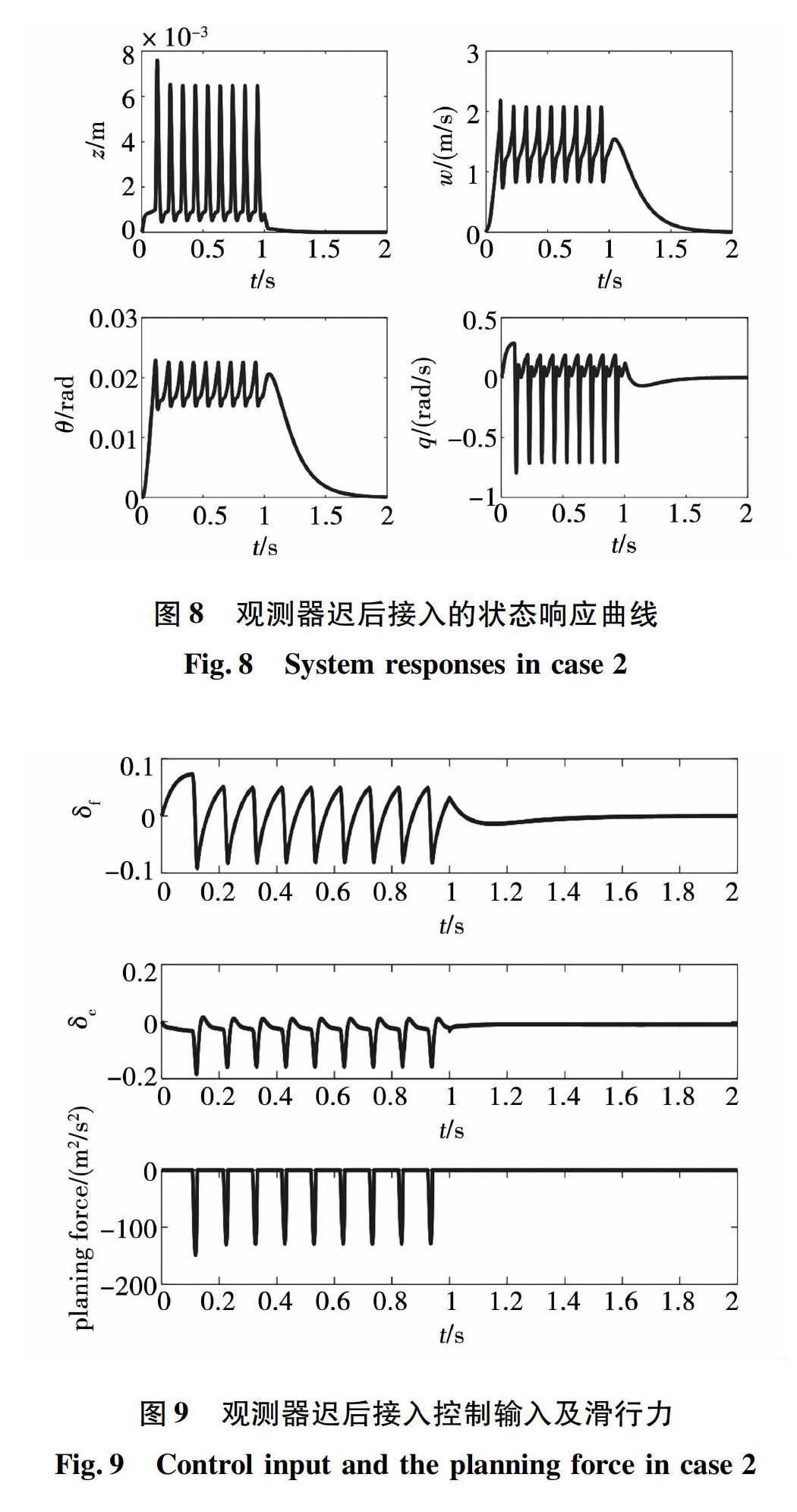
第2种情况:初始速度w(0)=0,航迹输入xeq=0,并迟后一秒接入观测器补偿。各个状态变量的响应曲线如图8所示,对应的控制输入及滑行力如图9所示。从图中可见,在未接入扰动观测器前,w在1 m/s和2 m/s之间波动,即在无滑行力和有滑行力之间波动(参见图2),而俯仰角θ的平均值为0.02 rad,即航行体是微微的抬着头,尾部周期性的拍打着空泡下壁高速前进,这就是当前的航行体在重力影响下典型工作模式。接入扰动补偿后,航行体很快平稳下来,体现了补偿的效果。在此过程中控制面的偏转角均小于0.2 rad,满足正常工作的范围。
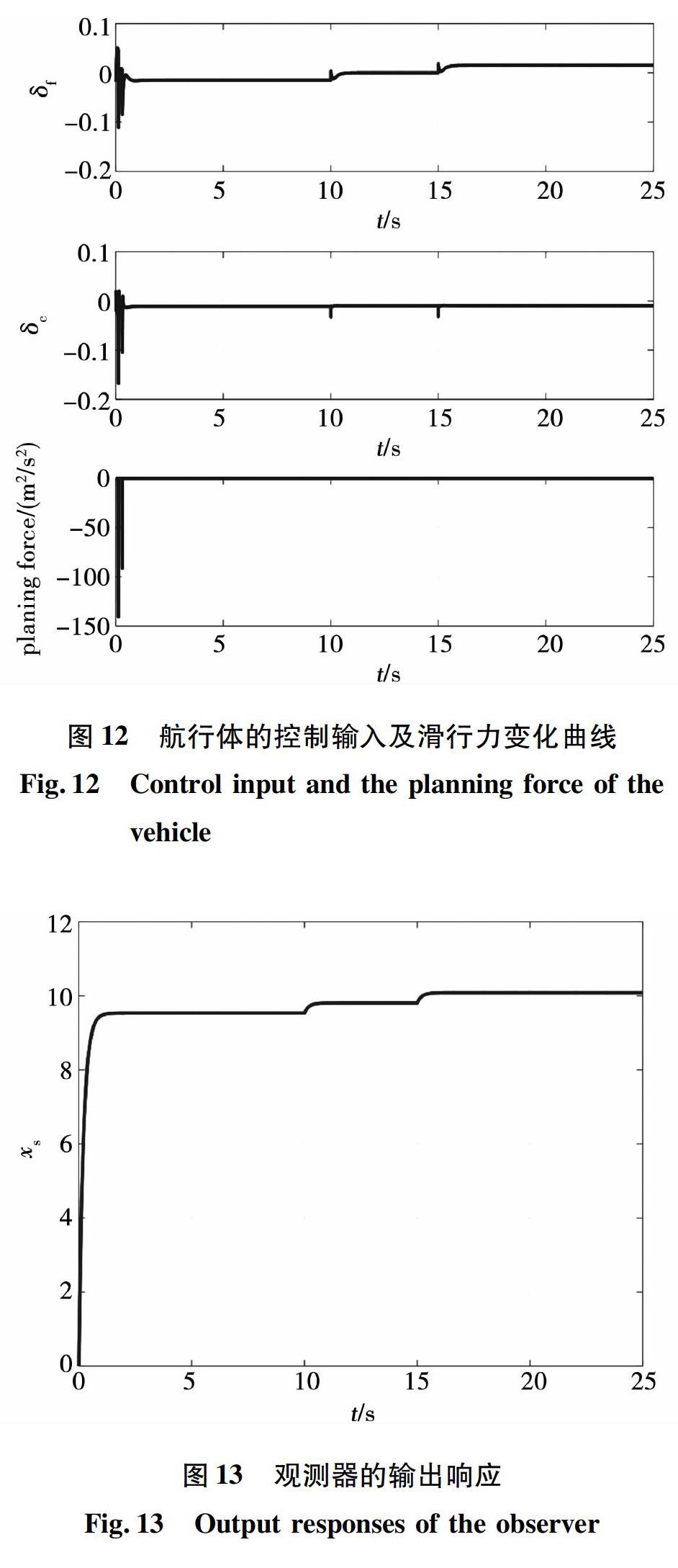
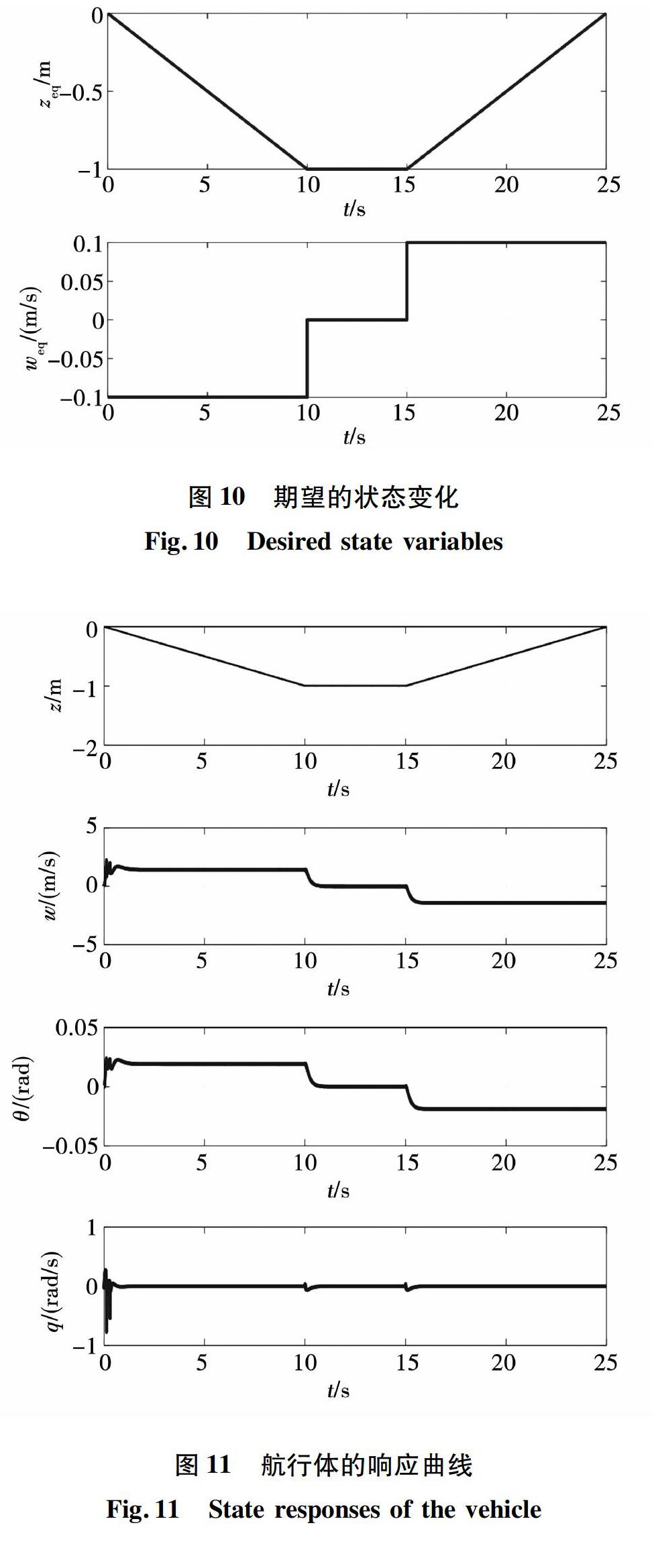
第3种情况:初始速度w(0)=0,轨迹输入xeq变化曲线如图10所示,即航行体以0.1 m/s的速度爬坡 (注:w、z向下为正方向),爬升至1 m后,保持5 s后,再以0.1 m/s的速度下降回到原来的深度。各个状态变量的响应曲线如图11所示, 从图中可见,除初始的过渡过程外,航行体按照预定的深度航迹平稳运行,不与空泡壁碰撞。对应的控制输入及滑行力如图12所示,图中显示,在此过程中控制面的偏转角均小于0.2 rad,满足实际工作要求。观测器输出如图13所示,从图中可见,x^s曲线在10 s和15 s上均有一个变化,这是由于航迹变化引起的。图11和图12表明,在整个航迹变化过程中已没有拍打现象,体现了补偿的效果。
4 结 论
超空泡航行体典型的工作模式是周期性拍打空泡壁高速前行的。这种周期性滑水现象产生的根源是重力的作用,如果补偿了重力,即可以避免航行体下沉与空泡壁碰撞产生滑行力。对于超空泡航行体来说,常值扰动还包含航迹控制中的平衡点变化问题,所以这个扰动是一个未知的变化着的扰动。采用扰动观测估计来补偿系统的常值扰动,可以避免滑行力的产生,从而消除周期性滑水的运行模式。本文所设计的控制器能够保证航行体与空泡壁不会连续碰撞,在空泡内平稳运行,且能够保证控制面的偏转角在正常工作范围内。
参 考 文 献:
[1] VASIN A D. The principle of independence of the cavity sections expansion (Logvinovich's principle) as the Basis for investigation on cavitation flows[C]// National Tax,AssociationTax,America. 2001:161-162.
[2] SANABRIA D E, BALAS G J, ARNDT R E A.Modeling, control, and experimental validation of a highspeed supercavitating vehicle[J]. IEEE Journal of Oceanic Engineering, 2015,40(2):362.
[3] SANABRIA D E, BALAS G J, ARNDT R E A. Planing avoidance control for supercavitating vehicles[C]// American Control Conference, 2014: 4979-498zz.
[4] MAO Xiaofeng, WANG Q. Delaydependent control design for a timedelay supercavitating vehicle model[J]. Journal of Vibration & Control, 2011,17(3):431.
[5] SAVCHENKO Y N. Control of supercavitation flow and stability of supercavitating motion of bodies[C]// Vki Lecture Series Supercavitating Flows, 2001:11.
[6] KIRSCHNER I N, KRING D C, STOKES A W, et al. Control strategies for supercavitating vehicles[J]. Journal of Vibration and Control, 2002, 8:219.
[7] DZIELSKI J, KURDILA A. A benchmark control problem for supercavitating vehicles and an initial investigation of solutions[J]. Journal of Vibration and Control, 2003:791.
[8] DZIELSKI J. Longitudinal stability of a supercavitating vehicle[J]. IEEE Journal of Oceanic Engineering, 2011:562.
[9] GUO Jianlin, BANACHANDRAN B, ABED E H. Dynamics and control of supercavitating vehicles[J]. Journal of Dynamic Systems, Measurement, and Control, 2008, 130(1):1.
[10] 王廣雄,何朕. 控制系统设计[M]. 北京:清华大学出版社,2005.
[11] LOGVINOVICH G V. Hydrodynamics of flows with free boundaries[M]. New York: Halsted Press, 1972.
(编辑:刘琳琳)
