基于可变温度模型的锂电池SOC估计方法

何耀　曹成荣　刘新天　郑昕昕　曾国建

摘 要：动力电池的荷电状态（stateofcharge，SOC）是电动汽车的重要参数之一，而准确的电池模型是提高SOC估算精度的前提。温度对电池相关参数的影响是目前研究的热点，然而现有的电池模型难以适应连续变化的温度环境，且测试工作量大。基于Nernst电化学方程，提出了一种新型的电池建模方法，运用统计学原理，通过测量较少的数据得到较为精确的电池模型，相关参数能够用包括连续变化的温度等多因素进行拟合。通过在不同温度环境下模拟电动汽车实际工况，对锂电池进行放电实验，通过试验设计的方法建立电池模型，结合扩展卡尔曼滤波算法实现对锂电池SOC的动态估计，仿真和实验结果验证了所提方法的优越性。

关键词：动力锂电池；荷电状态；Nernst模型；试验设计；扩展卡尔曼滤波

中图分类号：TM 315

文献标志码：A

文章编号：1007-449X（2018）01-0043-10

0 引 言

动力电池作为电动汽车的核心部件，其性能影响到整车性能。锂离子动力电池的荷电状态（stateofcharge，SOC）反映了其剩余电量的多少[1]。准确的估计电池的SOC能更有效地进行电池和整车管理，对预测电动车的行驶里程以及电池组的使用和維护有重要的意义[2-3]。

电池变化的电量为电流和时间的积分，根据SOC的定义，其等于电池初始电量与变化电量差值相对于电池总电量的百分比[4]；因此采用安时积分法能够实现SOC的实时估计，其也是目前应用最为广泛的一种SOC估计方法[5]。

然而，安时积分法是一种开环预测方法，受到采样误差、噪声干扰等因素的影响，根据安时积分法计算得到的SOC与实际值之间会存在一定的误差，并会随时间累积逐渐增大[6]。为解决该问题，先进的滤波算法被应用于SOC估计中，其实质是引入了输出反馈机制，将SOC的估计结果带入所建立的电池模型，将电池模型的理论输出值和检测到的实际值进行比较，误差信号经过调节后对输出SOC进行补偿，从而提高SOC估计的精度。文献[7]给出了一种神经网络法，具有实时在线估计的优势，但需要大量的训练数据。文献[8]提出了一种基于坐标变换的改进算法。文献[9]运用了采样点卡尔曼滤波算法。这些方法都从改进滤波算法的角度实现了SOC的高精度估算，然而，根据反馈机制，滤波算法的准确性在根源上取决于所建立的电池模型能否反应真实的电池特性。目前针对锂电池的建模主要包括等效电路模型和电化学模型，等效电路模型将电池内部等效为电压源、电阻和电容的串并联组合，文献[10-12]分别提出了Rint模型、Thevenin模型、PNGV模型；然而这些模型中的参数并非定值，不易进行参数辨识。电化学模型则直接通过电池内部的化学反应得到输入输出变量的关系式，各参量变化的影响因素明确，容易进行辨识；但是这些模型未考虑温度对电池SOC的重要影响，故具有一定的局限性。文献[13]通过温度补偿系数来改善了SOC估计模型，提高了SOC准确度，但未考虑电池内阻受温度影响这个重要因素。此外，在进行模型参数辨识时，需要进行大量实验，尤其是在考虑温度影响后，实验工作量成倍增加，这也是制约电池模型准确度的原因之一。

针对上述问题，本文提出了一种基于锂电池电化学模型的新型建模方法，利用统计学思想，通过尽量少的实验数据得到较为精确电池模型，在提高模型准确度的同时，减少了测试数据的工作量，缩短了建模周期。

文中首先通过电池的电化学模型分析了影响参数变化的因素，并采用试验设计（design of experiment，DOE）方法对各参数进行拟合，在此基础上，以电池SOC为状态变量，以电池端电压作为观测变量，采用扩展卡尔曼滤波（extended kalman filter，EKF）方法实时在线估计锂电池SOC。最后通过仿真和实验验证了所提出方法的准确性。

2 锂电池等效内阻的拟合方法

2.1 试验设计原理

若采用常规的数据拟合方法分析Rin和SOC、T的关系，需要大量的测试数据，通常测量一个特定温度和SOC下的内阻需要进行HPPC实验，即通过大电流放电测量某一温度下不同SOC时的电池内阻值；因此不同温度不同SOC需要耗费大量时间。但不同类型的锂电池等效内阻并不相同，耗费大量的测试时间无法得到通用的锂电池模型；因此并没有实际的工程意义。为解决该问题，可采用DOE方法，通过测量尽可能少的数据点得到较为精确的模型，在很大程度上缩短了建模周期，在参数拟合方面具有普适性，能够为不同类型的锂电池建模提供通用方案。

DOE是一种安排实验和分析实验数据的数理统计方法，目前多应用于数据统计，通过分析系统的各影响因素，以一个或多个设计目标为输出量，建立系统模型[16]。在建模过程中可以不需要考虑输入量和输出量之间的原理性关系，仅需设定不同的输入量值进行有限次数的试验，得到相应的输出量值，通过输入、输出量值进行关系式拟合。当实际输出量与输出量拟合值之差满足正态分布时，即可认为输入和输出的拟合关系（即系统模型）是准确的。这种方法建模所需实验量较少、结果较为精确，在航空航天、生物学、药学、企业产品生产和评估中有着广泛的应用。而中心复合设计（central composite designs，CCD）具有设计简单、系统性强等优点，在DOE应用中最为常见[17]。本文将基于CCD的DOE方法建立内阻模型，如图2所示，模型的输入量为SOC和温度T，输出量为等效内阻Rin。

输入量SOC的范围为[SOCmin，SOCmax]，输入量T的范围为[Tmin，Tmax]，在SOC和T组成的坐标系上，选取边界点和中心点进行试验。其中，边界点又分为平方点和轴向点。平方点处于两个输入量的边界上，对应图2中的A～D四个点；轴向点处于单个输入量的边界上，对应图中的E～H四个点；中心点处于两个输入量的中心处，对应图中的O点。各点的坐标分别为：

在统计学原理中，在一定的范围内的任何模型都可近似看作二次曲面，而验证范围选取合理性和模型精确性的方法则是计算拟合曲面和实验结果的残差，校检其是否符合6σ（六西格玛）正态分布[18]；因此，CCD的实质是通过试验测量各点对应的等效内阻Rin，并将试验结果拟合成表征Rin和SOC、T关系的二次曲面，并通过残差分布进行验证。

2.2 等效内阻的建模

等效内阻模型有两个输入变量SOC和T，因此可采用两水平因子试验设计。拟合的等效内阻模型包含SOC和T的交叉乘积项和一、二次项，其表达式为

Rin=Con+aT+bSOC+cT2+

dSOC2+eT·SOC+ε。（16）

其中：Con为常数项；ε为误差；a～e为常系数。

在DOE中，为了得到更加接近实际值的拟合曲面，需要在边界点和中心点的基础上对试验点进行适当的增补，因此所进行的试验并不局限于式（7）～式（15）对应的SOC和T值。图3给出了不同SOC和T对应的等效内阻Rin变化关系。图3（a）所示为不同温度对应的RinSOC曲线，在相同温度下，Rin随着SOC的减小而逐渐增大，但其变化并不明显。图3（b）所示为不同SOC和T对应的Rin等值线图，可以看出，不同温度下内阻的变化较大，因此，Rin不仅与SOC有关，还跟温度T有关。

图4为SOC和T对Rin的作用效应图，图4（a）为SOC和T的独立效应图，其表示单个因子在不同水平下的变化导致输出变量的平均变化，图中T对内阻均值的斜率高于SOC对内阻均值的斜率，说明温度T对Rin的作用更为显著。图4（b）为SOC和T的交互效应图，当一个因子的效应依赖于其他因子所处的水平时，则称两个因子间有交互效应，图中不同温度下SOC与Rin均值直线近似平行，在温度不同的情况下，SOC对电池内阻的影响方式不变，（温度变化时，并不会改变SOC对电池内阻的影响），说明T与SOC的交互效应并不显著，直观表现在式（16）中交叉乘积项的常系数e近似为0。

基于上述分析，在式（7）～式（15）对应的9个基本数据点的基础上，随机增加4个数据点，即通过13次测试进行等效内阻建模。其中，SOC的上下限分别为90%和10%，环境温度T的上下限分别为40 ℃和-20 ℃，表1给出了对应的测试数据。其中，ΔU为HPPC试验中所测得的电流脉冲导致的电池端电压压降，Rin可用ΔU除以电流脉冲幅值的计算结果进行等效。

将表1中的测试数据和相应的Rin计算结果进行CCD建模，可得到式（16）中各系数与常数项的拟合值。可以看出，交叉乘积项的常系数e近似为0，拟合结果与理论分析相一致。表2给出了各项系数。

图5为基于所建模型的Rin响应曲面。可以看出，Rin随SOC和T的增加而增加，且T变化对Rin的影响更加明显。

图6为Rin的残差直方分布图，残差为观测值与拟合值之差。图中残差值呈近似的正态分布，表明在所选取的范围内，计算出的内阻的模型对连续变化的输入变量T和SOC都适用。

3 适应温度变化的辨识参数k1、k2

为辨识参数k1和k2，应在不同条件下给出式（6）中其他参数的值，采用最小二乘法进行辨识。各参数的值需要在稳态下测定以保证辨识的准确性，对于式（6），IcRin（SOC，T）代表了电流流过电池内阻产生的压降，在充放电过程中，该项不可忽略。为保证稳态下测量，Ic和Rin都应为稳态值，Ic的稳态值即为恒流充放电的电流值，而Rin与SOC有关，恒流充放电时SOC始终在变化，无法得到Rin的稳态值。同理，式（6）中的ln（SOC）和ln（1-SOC）都无法在充放电过程中获得稳态值。

为解决SOC在充放电过程中始终变化而导致各参数稳态值无法获得的问题，需要通过测量开路电压进行k1和k2的辨识。电池在长时间静置的条件下，其开路电压与SOC有相对固定的函数关系，且SOC值近似不变；因此通过改变环境温度，对不同SOC下开路电压进行测量，可以得到各参数的稳态值，进而通过最小二乘法进行k1和k2的辨识[19]。且测量开路电压时Ic为0，可以省去IcRin（SOC，T）项，进一步简化计算量，此时式（6）可以简化为

U=E0+k1lnSOC+k2ln（1-SOC）。（17）

式中U即为电池的开路电压。通过对-15 ℃、-10 ℃、10 ℃、15 ℃、30 ℃下的电池放电数据进行分析，使用最小二乘法可以得出式（6）的参数拟合值，如表3所示。其中RMSE为均方根相对误差，其值较小，证明了拟合结果的精确性。

4 基于EKF的SOC估算方法

Kalman滤波算法是由Kalman提出的一种递推滤波方法，用于解决线性系统状态变量的最优估计问题。对于非线性系统的状态估计，首先建立系统的离散状态空间模型，用一阶Taylor近似展开使该状态空间模型线性化，进而应用Kalman算法实现对状态变量的最小方差估计，称为扩展Kalman滤波法（EKF）[20]。

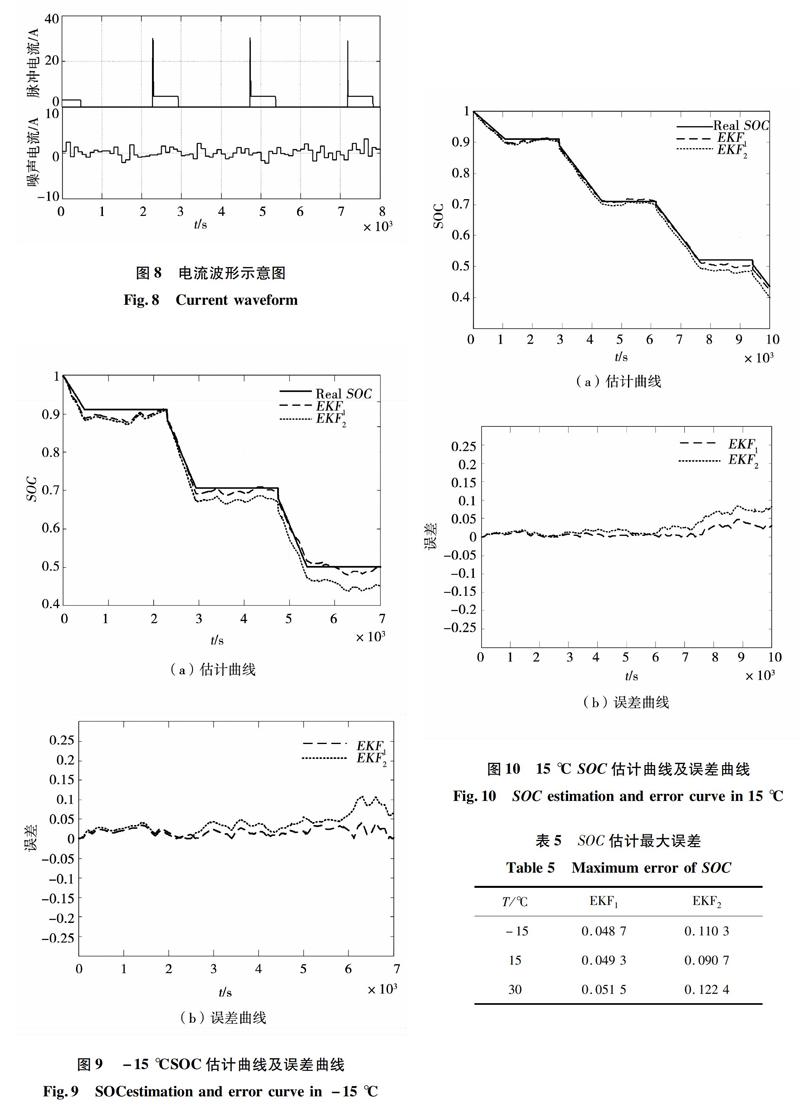
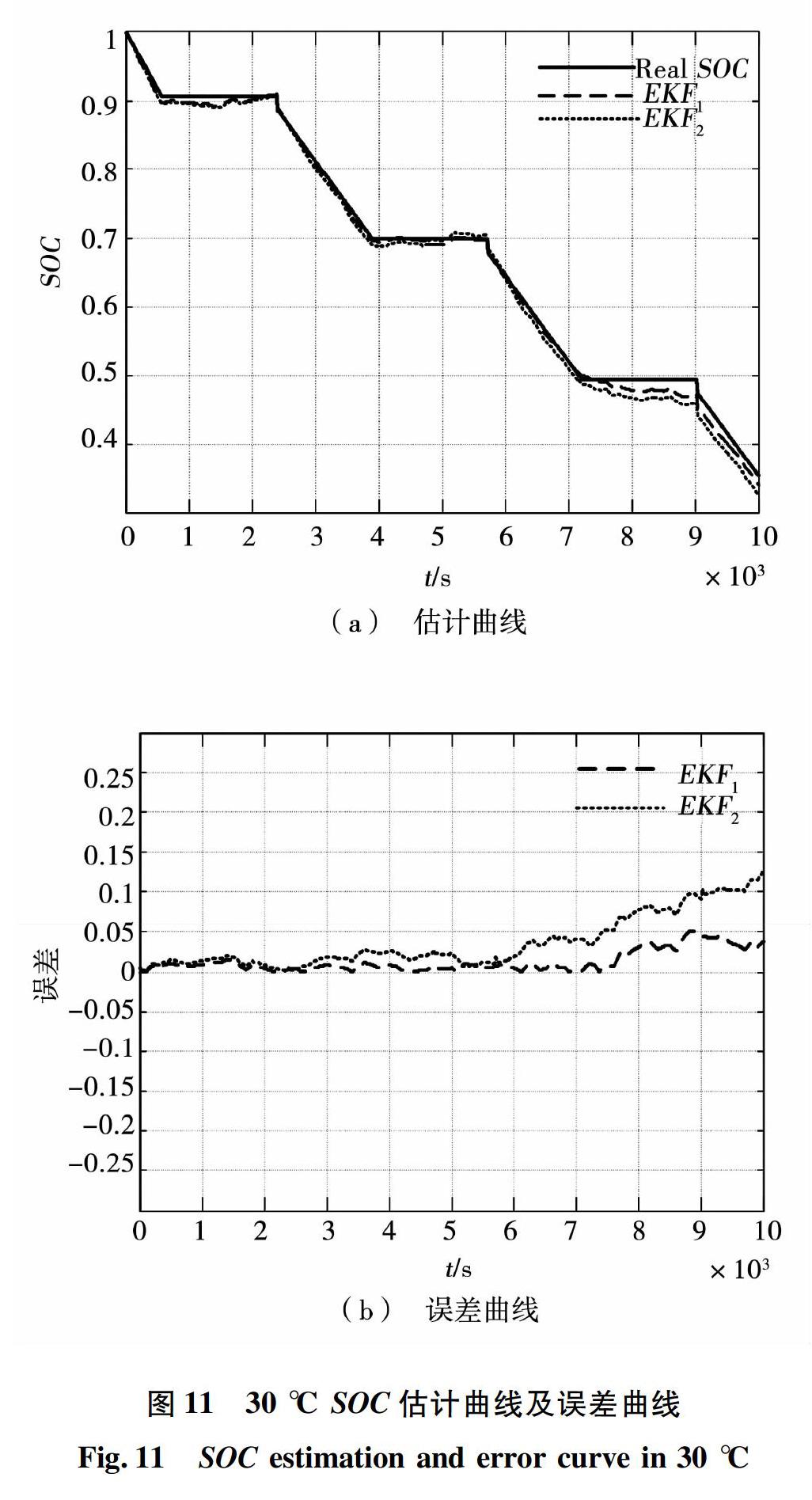
使用卡尔曼滤波算法估计电池SOC时，首先建立电池的离散状态空间模型，进而完成初始值設定、更新、测量更新以及求取卡尔曼增益等步骤。以上述放电过程中的得到的电池放电电流、电池端电压数据为基础，利用表2和表4中的参数，在Matlab/SIMULINK中建立电池SOC估算模型，分别在-15 ℃、15 ℃、30 ℃的温度下进行仿真验证，并将由所提出估算方法获得的SOC估计值（EKF1）与传统基于Nernst模型的SOC估计值（EKF2）进行比较，结果如图9～图11所示。

表5给出了对应的SOC估计最大误差值，可以看出，基于改进的Nernst模型，在使用相同估算方法EKF条件下，SOC估算精度均提高。特别是当环境温度较低或较高时，温度对电池性能的影响远高于常温时温度对电池性能的影响，并且根据上述各图可以看出，适应可变温度的估计方法能明显减小SOC估计误差。

6 结 论

本文针对温度对电池性能的影响，在单体电池的电化学模型基础上，运用了DOE试验设计方法分析了电池內阻的变化规律，进而得到改进的Nernst模型，并使用EKF算法估计电池SOC。所提出的方法具有以下优势：

1）采用DOE方法能够通过测量较少的数据得到较为精确的模型，在减少测试所需工作量的同时提高了SOC估算精度；

2）在环境温度处于较高或较低时，电池模型的修正效果更为明显；

3）电池模型能够更加精确的适应连续变化的温度，增大了该模型的使用范围，为SOC的估计带来方便。

参 考 文 献：

[1] XING Yin， HE Wei， PECHT M， et al. State of charge estimation of lithiumion batteries using the opencircuit voltage at various ambient temperatures[J]. Applied Energy， 2014， 11（3）：106.

[2] ZHONG Liang， ZHANG Chenbin， HE Yao， et al. A method for the estimation of the battery pack state of charge based on inpack cells uniformity analysis[J].Applied Energy，2014，1（13）：558.

[3] MICHELP H， HEIRIES V. An adaptive sigma point Kalman Filter hybridized by support vector machine algorithm for battery SOC and SOH estimation[C]//Boston：Vehicular Technology Conference，2015：1-7.

[4] 冯飞， 宋凯， 逯仁贵， 等. 磷酸铁锂电池组均衡控制策略及荷电状态估计算法[J]. 电工技术学报， 2015， 30（1）： 22.

FENG Fei， SONG Kai， LU Rengui，et al. Equalization control strategy and SOC estimation for LiFePO4 battery pack[J]. Transactions of China Electrotechnical Society， 2015， 30（1）： 22.

[5] 李哲， 卢兰光， 欧阳明高. 提高安时积分法估算电池SOC精度的方法比较[J]. 清华大学学报（自然科学版）， 2010，50（8）：1293.

LI Zhe， LU Languang， OUYANG Minggao. Comparison of methods for improving SOC estimation accuracy through an amperehour integeration approach[J]. Journal of Tsinghua University Science & Techrwlogy，2010，50（8）：1293.

[6] HE Yao， ZHANG Chenbin， LIU Xintian， et al. SOC estimation for LiFePO4 highpower batteries based on the information fusion[J]. Control and Decision， 2014， 29（1）： 189.

[7] CHARKHGARDM， FARROKHI M. Stateofcharge estimation for lithiumion batteries using neural networks and EKF[J]. IEEE Transactions on Industrial Electronics， 2010， 57（12）： 4178.

[8] 陈健， 万国春， 毛华夫. 基于多模型的电池SOC估计算法的研究[J].电源技术，2013，37（2）：251.

CHEN Jian， WAN Guochun， MAO Huafu. Study of battery SOC prediction based on multimodel[J].Chinese Journal of Power Source，2013，37（2）：251.

[9] 高明煜， 何志伟， 徐杰. 基于采样点卡尔曼滤波的动力电池SOC估计[J]. 电工技术学报， 2011， 26（11）： 161.

GAO Mingyu， HE Zhiwei， XU Jie.Sigma Point Kalman Filter based SOC estimation for power supply battery[J]. Transactions of China Electrotechnical Society， 2011， 26（11）：161.

[10] HE Hongwen， ZHANG Xiaowei， XIONG Rui， et al. Online modelbased estimation of stateofcharge and opencircuit voltage of lithiumion batteries in electric vehicles[J]. Energy， 2012， 39（1）： 310.

[11] 魏克新， 陈峭岩. 基于多模型自适应卡尔曼滤波器的电动汽车电池荷电状态估计[J]. 中国电机工程学报， 2012， 32（31）： 19.

WEI Kexin， CHEN Qiaoyan. Electric vehicle battery SOC estimation based on multiplemodel a daptive Kalman Filter[J].Proceedings of the CSEE， 2012， 32（31）： 19.

[12] LESLIEK， DEMIRKIRAN I， RASK E， et al. An investigation into the PNGV battery model with the addition of a dynamic temperature range[C]//Norfolk：Southeastcon，2013 Proceedings of IEEE，2013：1-6.

[13] HUSSEINA A. Experimental modeling and analysis of lithiumion battery temperature dependence[C]//Charlotte：Applied Power Electronics Conference and Exposition（APEC），2015：1084-1088.

[14] 毕军，康燕琼， 邵赛. 纯电动汽车动力锂电池Nernst模型参数辨识[J]. 汽车工程，2015，37（6）：725-730.

BI Jun， KANG Yanqiong， SHAO Sai. Parameters identification of nernst model for power Liion battery of pure electric vehicles[J].Automotive Engineering，2015，37（6）：725-730.

[15] 刘记. 全钒液流电池双极板流道的优化及流量控制研究[D].吉林：吉林大学， 2011.

[16] ZHENG Xinxin， XIAO Lan， MENG Xin， et al. Optimization of LCL filter based on THD estimation model[C].Denver， Colorado：Energy Conversion Congress and Exposition（ECCE）， 2013.

[17] 杨铭. Minitab用于中心复合设计与数据处理[J]. 药学服务与研究， 2007， 7（3）： 231.

YANG Ming. Minitab for central composite design and data processing[J]. Pharmaceutical Care and Research， 2007， 7（3）： 231.

[18] GIJO E V，SCARIA J，ANTONY J.Application of six sigma methodology to reduce defects of a grinding process[J]. Quality and Reliability Engineering International， 2011， 27（8）：1221.

[19] 梁志國， 朱振宇. 非均匀采样正弦波形的最小二乘拟合算法[J]. 计量学报， 2014， 35（5）：494.

LIANG Zhiguo， ZHU Zhenyu. The sinewave fit algorithm based on total leastsquare method with nonuniform sampling[J].Acta Metrologica Sinica， 2014， 35（5）： 494.

[20] 刘新天， 刘兴涛.基于VminEKF的动力锂电池组SOC估计[J]. 控制与决策， 2010， 3（25）：445.

LIU Xintian， LIU Xingtao. BasedVminEKF SOC estimation for power Liion battery pack[J].Control and Decision， 2010， 3（25）： 445.

[21] CHARKHGARDM， FARROKHI M. Stateofcharge estimation for lithiumion batteries using neural networks and EKF[J].IEEE Transactions on Industrial Electronics，2010， 57（12）： 4178.

（编辑：张 楠）