基于内含传感器的两电机调速系统神经网络左逆张力辨识
2018-05-14刘国海陈杰赵文祥袁骏徐亮
刘国海 陈杰 赵文祥 袁骏 徐亮

摘 要:针对两电机调速系统高精度张力传感器价格昂贵、安装要求高、材料和环境限制多的问题,提出基于“内含传感器”的神经网络左逆张力软测量方法。为实现两电机调速系统张力辨识,基于“内含传感器”的概念,建立“内含传感器”张力子系统,并证明其数学模型的左可逆性。考虑到逆系统模型较为复杂,存在参数时变的特点,采用BP神经网络精确逼近张力左逆模型,并串联在原系统之后,实现张力的辨识。基于两电机实验平台,对张力辨识效果进行仿真及实验验证,研究结果表明,该策略能够快速、精确地跟踪张力实际值,且易于实现。
关键词:内含传感器;神经网络左逆;两电机调速系统;张力辨识
中图分类号:TM 343
文献标志码:A
文章编号:1007-449X(2018)01-0023-06
0 引 言
多电机变频调速系统具有多输入多输出、高阶、非线性、强耦合的特点,被广泛应用于冶金、造纸、纺织、轨道交通、印刷等现代工业领域[1-4],这类系统需要多台电机来传送和抓取物料,张力的稳定是保证传送和抓取效率的重要因素。稳定的张力不仅能够保证物料不会因过紧而拉断,而且能够保证物料不因松弛而堆积。传统的方法是通过安装张力传感器来实现张力的检测和控制;但是高精度的张力传感器价格比较昂贵,且安装要求高,材料和环境限制因素多,严重限制系统的应用与推广。所以,实现张力的软测量是多电机协调控制领域需要解决的问题。
为此,国内外许多相关领域的学者对多电机变频调速系统的张力辨识做了很多工作。文献[5]和文献[6]使用摩擦转矩、电磁转矩和惯性转矩来辨识双鼓式复卷机的张力;文献[7]根据两电机直流驱动系统时变偏差方程设计了张力非线性降阶状态观测器;文献[8]通过复卷机的卷径、转速、加速度和动态转矩的全阶状态观测器对系统张力进行辨识;文献[9]基于纸复卷机收卷和放卷变量建立观测模型对张力进行辨识,并通过监控当前辨识值与前一时刻参数估计值的误差来保证张力观测的准确性。但是,上述方法都基于系统精确的数学模型,运行过程中受到参数变化和各种内外干扰,影响辨识的准确性。
多电机变频调速系统是一个多输入多输出、高阶、强耦合的非线性系统,难以得到精确的数学模型,且存在模型参数变化和受到各种内外扰动的情况[10-11],因此有必要研究不依赖系统精确数学模型的辨识策略。近年来提出的基于“内含传感器”的左逆软测量方法[12]可以通过函数逼近来实现不可测变量的辨识。神经网络可以以任意精度逼近非线性函数[13-15],本文利用基于神经网络左逆的张力辨识策略,把神经网络逼近任意非线性函数的特点与逆系统方法具有解耦和线性化的特点相结合,不依赖系统精确的数学模型,克服建模误差,具有清晰直观的物理意义。本文以两电机变频调速系统为例,首先证明系统的可逆性,在理论上验证该策略的可行性。然后构建两电机变频调速系统模型,通过仿真对张力进行辨识。最后通过实验验证该策略的实际可行性。
1 基于“内含传感器”的神经网络左逆软测量原理
考虑如下的非线性系统:
x·=f(x,u)。(1)
設x^=[x1,x2,…,xl]T为不直接可测变量,z=[xl+1,xl+2,…,xn]T为直接可测变量,为了实现利用直接可测变量来估计不直接可测变量,假设系统中存在一个“内含传感器”子系统,其输入为不直接可测变量x^,输出为直接可测变量z,若“内含传感器”左可逆,则可得到“内含传感器”左逆系统,将其串联在“内含传感器”子系统之后得到复合系统,输出为不直接可测变量x^,如图1所示,即其复合系统能够对不直接可测变量进行观测,具有软测量仪表的功能。
但在实际应用中,多数非线性系统都比较复杂,很难得到其精确的数学模型;而神经网络是一种能够对数据进行并行处理的算法,具有很强的学习和自适应能力,能够以任意精度逼近非线性函数。因此使用神经网络来逼近“内含传感器”左逆系统,可以有效解决精确的数学模型无法获取的问题。常用神经网络有径向基函数神经网络(radial basis function neural network,RBFNN)和反向传播神经网络(back propagation neural network,BPNN)等,由于RBF网络的训练需要动态确定网络结构和隐含层节点数目,考虑到实际硬件的限制,本文选择BP网络来逼近“内含传感器”左逆系统,BP网络结构如图2所示,对于具有p维输入q维输出的三层BP网络,隐含层节点数为N,其输出为
yok=f2(∑Nj=1(f1(∑pi=1Riwij+θj)wjk+θk),k=1,2,…,q。(2)
式中f1(·)和f2(·)分别为隐含层和输出层激活函数,每个神经元具有相应的权值w、阈值θ,权值和阈值可通过神经网络学习算法自动调整,从而使整个神经网络逼近目标非线性函数。
2 数学模型
考虑典型的两电机变频调速系统,其物理模型如图3所示。
由于无法得到系统精确的数学模型,且存在模型参数变化以及未建模动态部分,如矢量变频器的转子角速度误差,因此“内含传感器”的左逆系统难以实现,限制了其应用。神经网络能够以任意精度逼近非线性函数,且不依赖系统精确的数学模型,因此将神经网络与“内含传感器”左逆方法相结合,可以有效解决左逆方法依赖精确数学模型的问题,并且能够学习系统的未建模动态的规律,增强系统的抗干扰能力。神经网络左逆软测量模型结构如图5所示。
4 仿真验证
在Matlab环境中使用SFUNCTION函数构建两电机调速系统的数学模型,分别设计转速和张力PID控制器使系统稳定,为充分激励出两电机调速系统在各频段的动静态特性,使输入输出尽可能覆盖整个工作区间,转速给定为150~500 r/min的随机方波,张力给定为100~600 N的随机方波,同时采集相应的输入输出信号{ω1,ω2,ωr2,ω·r2,F}。张力的激励和响应波形如图6所示。
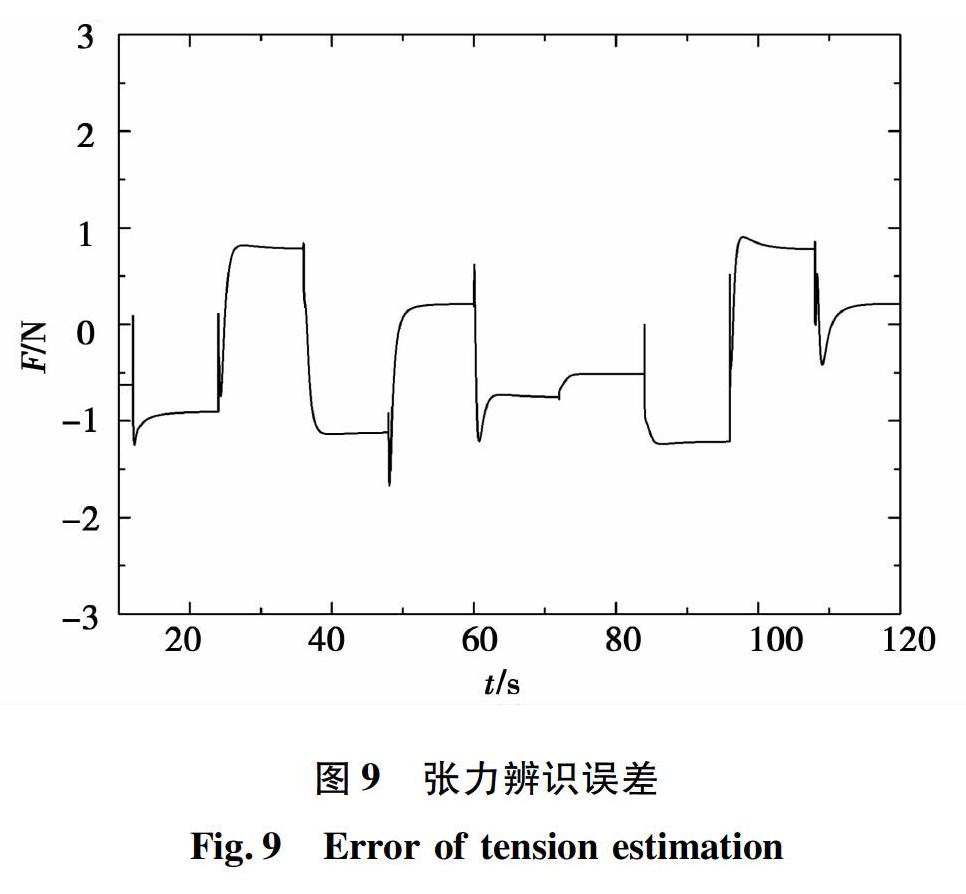
本文采用3层BP网络,隐含层节点数为15个,对采样数据进行掐头去尾,使用Matlab工具箱对神经网络进行训练,将得到的神经网络串联两电机调速系统之后,实现对张力的软测量。神经网络左逆张力辨识框图如图7所示。转速给定为200~400 r/min随机方波,张力给定为150~400 N随机方波,采集两电机调速系统实际张力与神经网络左逆辨识的张力进行比较,如图8所示,辨识张力与实际张力间误差如图9所示。
5 实验验证
实验平台包括研华上位机、西门子WinCC V6.0、西门子S7-300 PLC、数字量输入模块SM321、模拟量输入模块SM335、计数器模块FM350、2台2.2 kW的三相异步电机以及2台西门子MW440变频器。平台及其结构如图10所示。
实验平台通讯采用Profibus DP通讯协议,可在不同的兼容设备运行。实验过程中,在PLC中编写程序实现两电机调速系统的PID控制算法,并通過Profibus DP控制变频器,变频器设置为矢量模式。为充分激励出系统在各频段的动静态特性,使输入输出尽可能覆盖整个工作区间,采样过程中转速给定为150~500 r/min的随机方波,张力给定为120~400 N的随机方波,WinCC通过MPI接口将{ω1,ω2,ωr2,F}从PLC采集到Excel中,Matlab调用Excel中采样数据离线计算ωr2的一阶导数,对采样数据掐头去尾,并使用Matlab工具箱进行训练,训练完成后将神经网络权阈值导入至PLC中实现对张力的软测量。
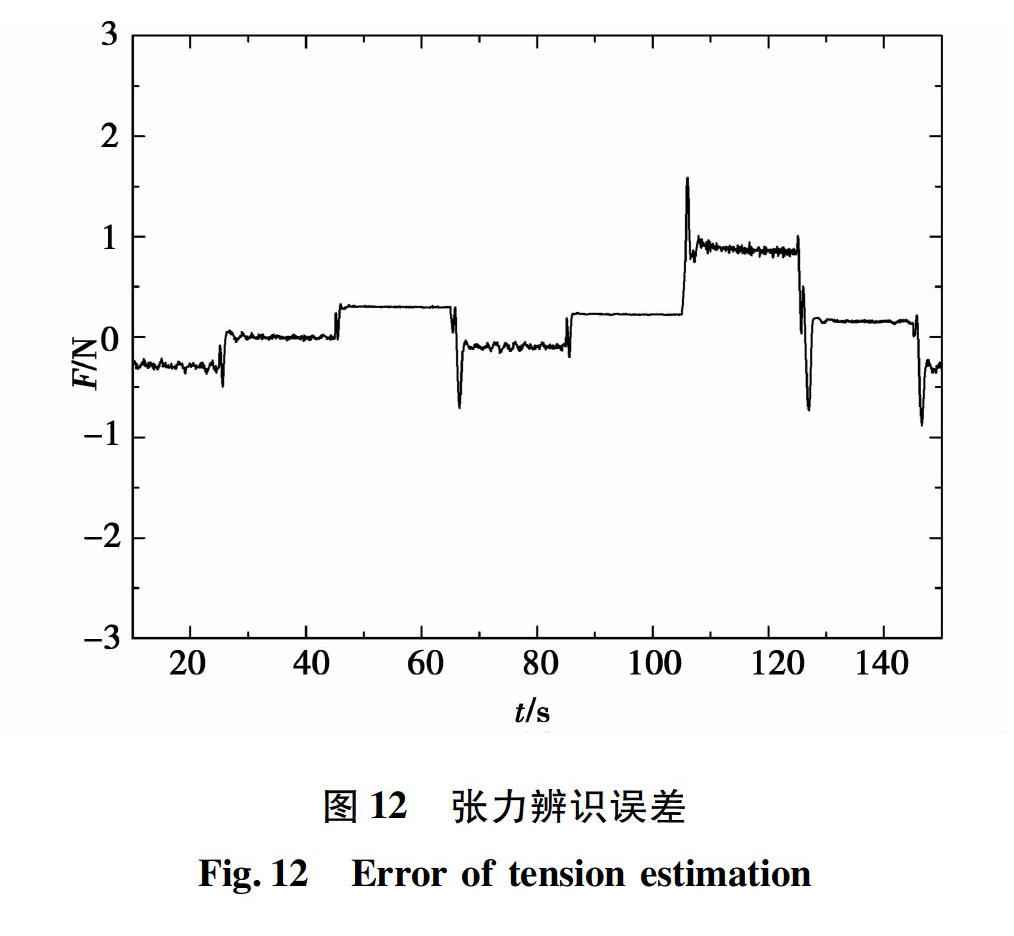
实验中转速给定200~400 r/min的随机方波,张力给定150~350 N的随机方波,采集传感器实测张力和神经网络左逆辨识的张力,如图11所示,辨识张力与实际张力间误差如图12所示。从实验结果可以看出,张力辨识值能够快速跟踪实际张力,张力最大辨识误差在0.669%,说明本文提出的神经网络左逆张力辨识策略可行有效。
6 结 论
本文基于“内含传感器”的概念提出了神经网络左逆软测量方法。利用神经网络不依赖系统精确数学模型以及能够精确逼近非线性函数的特点,逼近两电机变频调速系统的张力“内含传感器”子系统,实现张力的软测量。仿真和实验结果表明,神经网络左逆辨识的张力能够快速、精确地跟踪实际值,且系统不需要添加额外的硬件,易于实现,适合张力传感器安装困难的场合。
参 考 文 献:
[1] CHEESHEE LIM, LEVI E, JONES M, et al. A comparative study of synchronous current control schemes based on FCSMPC and PIPWM for a twomotor threephase drive[J]. IEEE Transactions on Industrial Electronics, 2014, 61(8):3867.
[2] DORREL D, PARSA L, BOLDEA I. Automotiveelectric motors, generators and actuator drive systems with reduced or no permanent magnets and innovative design concepts[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10):5693.
[3] CAI Haiwei, GUAN Bo, XU Longya. Lowcost ferrite pmassisted synchronous reluctance machine for electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5741.
[4] CAO Ruiwu, CHENG Ming,HUA Wei. Investigation and general design principle of a new series of complementary and modular linear FSPM motors[J]. IEEE Transactions on Industrial Electronics, 2013, 60(12):5436.
[5] ABJADI N R, SOLTANI J,ASKARI J. Nonlinear slidingmode control of a multimotor webwinding system without tension sensor[J]. IET Control Theory and Applications, 2009, 3(4):419.
[6] CARRASCO R, VALENZUELA M A. Tension control of a twodrum winder using paper tension estimation[J]. IEEE Transactions on Industry Application, 2006, 42(2):618.
[7] LYNH A F,BORTOFF S A,ROBENACK K.Nonlinear tension observers for web machines[J].Automatica,2004,40(9):1517.
[8] VALENZUELA M A, BENTLEY J M, LORENZ R D. Dynamic online sensing of sheet modulus of elasticity[J]. IEEE Transactions on Industry Applications, 2010, 46(1):108.
[9] VALENZUELA M A, CARRASCO R, SBARBARO D. Robust sheet tension estimation for paper winders[J]. IEEE Transactions on Industry Applications, 2008,44(6):1937.
[10] 刘国海,薛剑锋,康梅,等.两电机调速系统神经网络广义逆在线调整控制[J].電机与控制学报,2009,13(4):511.
LIU Guohai, XUE Jianfeng, KANG Mei, et al. Online adjustment control of two motor speedregulating system based on neural network generalized inverse[J]. 2009,13(4):511.
[11] 张今朝,刘国海,潘天红.多电机同步系统的多模型辨识[J].电机与控制学报,2009,13(1):138.
ZHANG Jinzhao, LIU Guohai, PAN Tianhong. Multimodel identification to multimotor synchronous system[J]. Electric Machines and Control, 2009, 13(1):138.
[12] 蒋彦,刘国海,赵文祥,等.基于TDNNLI的永磁同步电机转速辨识[J].电机与控制学报,2014,18(2):62.
JIANG Yan, LIU Guohai, ZHAO Wenxiang, et al. Speed identification of permanent magnet synchronous motor by using TDNNLI method[J]. 2014,18(2):62.
[13] ANDRAS P.Function approximation using combined unsupervised and supervised learning[J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(3):495.
[14] 戴先中,刘国海,张兴华.交流传动神经网络逆控制[M].北京:机械工业出版社,2007:120-134.
[15] RAZAVI S, TOLSON B A. A New formulation for feedforward neural networks[J]. IEEE Transactions on Neural Networks, 2011,22(10):1588.
(编辑:刘琳琳)
