实时无隙钢球精密传动空间速度矢模型
2018-05-14段利英安子军付志强
段利英 安子军 付志强
1.燕山大学机械工程学院,秦皇岛,066004
2.天津科技大学包装与印刷工程学院,天津,300222
0 引言
实时无隙钢球精密传动系统中,组合行星盘中的弹性体可以实时调节钢球与摆线槽间的间隙,使精密机构具有实时无隙传动、精度高等特点,广泛应用于航空遥感相机位移补偿传动机构[1]及机器人伺服传动机构。
钢球精密传动装置通过组合行星盘中的弹性体调节构件轴向位置、消除啮合副的间隙来提高传动精度。新传动装置啮合处增加了实时变化的轴向位移和轴向力,啮合过程中产生的扭转变形和热变形导致啮合点并不在一个平面上。由于以上特点和多齿啮合的不对称性,活动钢球相对于中心盘和组合行星盘的运动是复杂的空间啮合运动,同时也是精密传动研究关键部分。将摆线钢球啮合副投影到端平面上不能详细描述精密钢球传动的空间啮合副。为了更详尽地描述啮合情况,需要建立空间速度矢模型。
HIDETSUGA[2]将钢球精密传动应用于机器人关节,并给出了减速器理论效率的计算方法,开发了三种无侧隙减速器并用矢量分析法描述了运动原理。AN等[3]利用超静变形协调条件推导出了摆线槽啮合副和环啮合副的最大作用力公式。宜亚丽等[4]利用弧长差分析了啮合副的滑动特性。张鹏等[5-6]建立了啮合副的非线性力学模型和摆线钢球行星传动系统的平移-扭转耦合动力学模型。杨荣刚等[7]建立了纯扭转强非线性动力学模型。孙鹏飞等[8]计算了钢球与齿面接触域的瞬时生热率和瞬时摩擦温升。以上研究都是建立在将钢球运动简化,将啮合副投影到平面上的基础上的。但以上方法不能精确描述实时无隙钢球精密传动系统的空间啮合情况。
甘屹等[9]利用D-H坐标系建立了6R型机器人工作空间的三维仿真模型。CONTE等[10]利用D-H法建立了一种激光跟踪仪的运动学模型。LI等[11]利用D-H方法表示了一个由几个链接组成的机构中最后一个关节相对于第一个关节的位置和方向。
本文利用修正D-H矩阵求解了钢球上任意一点相对于中心盘和组合行星盘的位置。根据空间几何建模法和传动特性,建立了钢球与中心盘和组合行星盘相对滑动速度矢模型,并分析了槽形角和钢球数对速度矢模型的影响。通过与仿真结果对比分析,验证了空间速度矢模型的可靠性。
1 传动机构
图1为实时无隙钢球精密传动机构的装配分解图。减速机构中,中心盘2的左端面上加工有齿数为Z1的外摆线槽,组合行星盘4的右端面上加工有齿数为Z2的内摆线槽。在内外摆线槽的交错区域内等距装有钢球3,钢球3总数为Zb=(Z1+Z2)/2。其传动原理在文献[12]中有详细的描述。
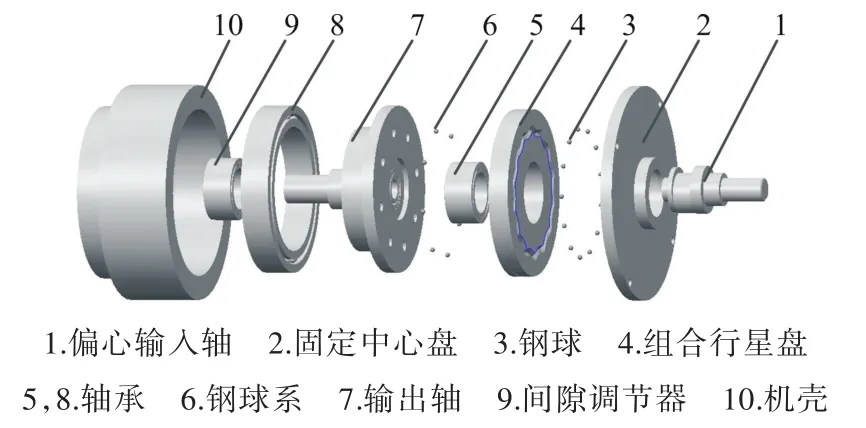
图1 实时无隙钢球精密传动机构的装配分解图Fig.1 Explode figure of assembly body of non-clearance ball precision transmission
2 D-H坐标变换矩阵
图2是传动机构减速部分空间运动坐标系。S1{O1x1y1z1}为空间固定坐标系,将S1{O1x1y1z1}沿 y1轴平移 e,沿 z1轴反向平移 e1,得到动坐标系S3{O3x3y3z3},其中e为偏心距的1/2,e1为中心盘与组合行星盘的轴向间距的1/2。O1O3视为连杆1,其长度用lO1O3表示。将S3沿 y3轴平移 e,沿着 z3轴反向平移 e1,得到动坐标系S2{O2x2y2z2},O3O2视为连杆2,其长度用lO3O2表示。
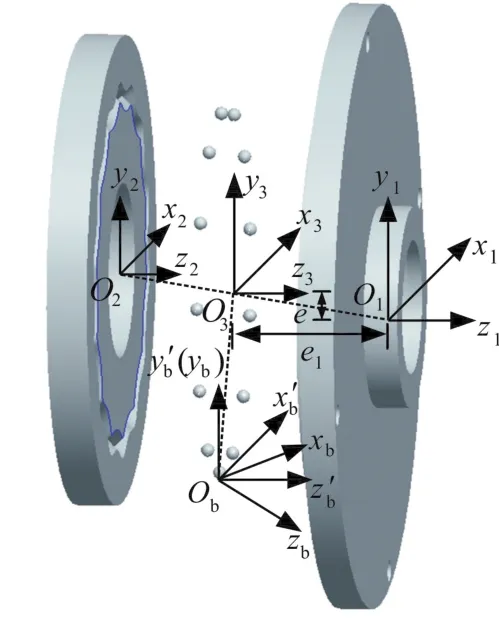
图2 机构减速部分空间坐标系Fig.2 Space coordination system of deceleration part
将S3沿钢球分布圆半径平移至第i个钢球的球心Ob,得到动坐标系,O3Ob视为连杆3,其长度用表示。将坐标系绕轴顺时针旋转角度 β得到坐标系坐标系ʹ到Sb长度视为连杆4,得到D-H参数如表1所示。

表1 D-H参数表Tab.1 D-H parameter table
表1中,φ1为S3绕 z1轴旋转的角度,为S2绕 z1轴旋转的角度,φ3为Sb绕 z3轴旋转的角度。坐标系Sb到空间动坐标系S2的变换矩阵为

其中,cβ表示 cosβ,sβ表示 sin β,余类似。
3 相对速度矢模型
3.1 钢球与中心盘的相对速度矢模型
钢球与中心盘之间相对运动,其运动关系如图3所示。S1为空间固定坐标系,坐标系S3绕中心盘轴线z1轴做行星运动,角速度为ω1。与动坐标系S3固连的钢球除绕zb轴自转外,还绕z3轴公转,角速度分别为ωb、ω3。采用反转法确定钢球与中心盘的相对运动,即对图3所示机构加-ω1,使其绕 z1轴回转。这时,中心盘绕 z1轴自转,角速度为-ω1。坐标系S3视为不动,钢球绕zb轴自转,又绕z3轴做行星运动。钢球上任意一点 B(x,y,z)相对中心盘的速度矢量为[13]


图3 钢球相对中心盘的运动关系Fig.3 Moving relationship between ball and the center disc
3.2 钢球与行星盘的相对速度矢模型
组合行星盘在偏心轴的带动下,绕中心盘z1轴线旋转,角速度为。同时组合行星盘还以角速度绕z2轴自转。钢球绕zb轴自转的同时,还绕 z3轴公转,角速度分别为ωb、ω3。钢球分布圆所在坐标系S3绕行星盘的轴线z2轴以角速度ω2旋转,如图4所示。同理,用反转法确定钢球相对于组合行星盘的运动。对整个机构加,使其绕 z1轴旋转,这时组合行星盘以绕 z2轴自转,钢球以ωb绕 zb轴自转,以ω3绕 z3轴公转。钢球分布圆所在坐标系S3以ω2绕z2轴旋转,同时又以绕z1轴旋转。
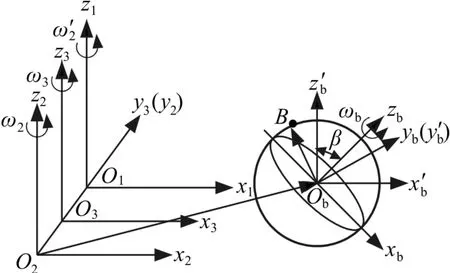
图4 钢球相对行星盘的运动关系Fig.4 Moving relationship between ball and the combination planet disc
同理可以求出钢球上任意一点 B(x,y,z)相对于行星盘的速度矢量:

4 数值模拟及参数分析
4.1 钢球与摆线槽相对速度数值模拟
钢球在摆线槽内滚滑,同时与中心盘和组合行星盘接触。
图5为啮合副沿公法线剖开图,钢球与中心盘以及组合行星盘内外两侧接触点分别为

图5 啮合副剖面图Fig.5 Cross section of meshing pair
在坐标系Sb下,钢球与摆线槽的啮合点分别为 Aʹ(0,0,rb)、B(rb,0,0)、Bʹ(-rb,0,0)、A(0,0,-rb)。根据坐标变换矩阵(式(1)),在坐标系S2下

同理,可得

取分布圆半径r0=2 mm,短幅系数K=0.42,直母线铣刀槽形角 β=45°,钢球半径rb=1.5 mm,内摆线槽齿数Z2=12,钢球数Zb=11,外摆线槽齿数 Z1=10。偏心输入轴角速度根据第二类椭圆积分E以及式(2)和式(3),可以得到钢球相对于中心盘在啮合点Bʹ、Aʹ点的转动速度如图6所示,钢球相对于行星盘在啮合点B、A的相对速度如图7所示。
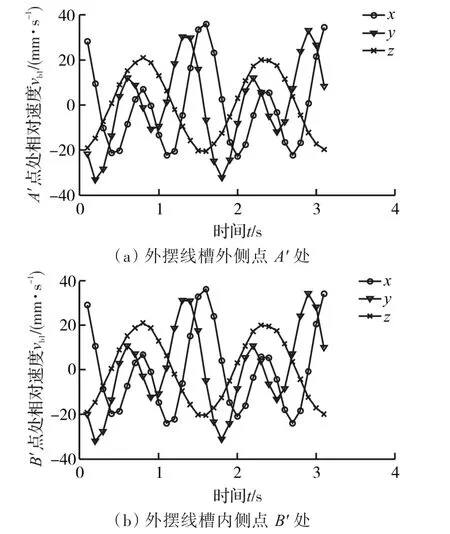
图6 钢球与中心盘相对速度矢vb1变化曲线Fig.6 Curve of relative velocityvb1between ball and the center plate
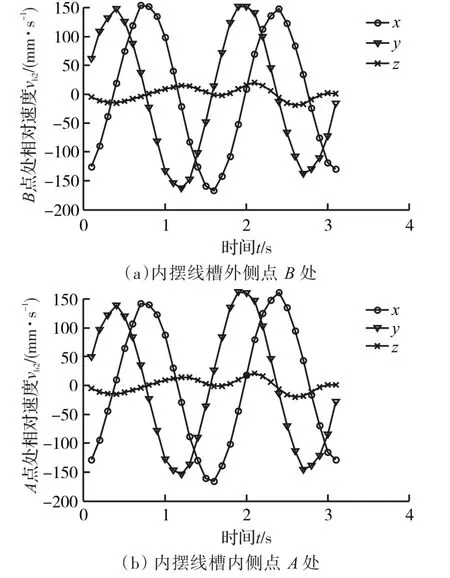
图7 钢球与组合行星盘相对速度矢vb2变化曲线Fig.7 Curve of relative velocityvb2between ball and the combined planet plate
由图6、图7可以看出,在啮合过程中,相对速度矢随时间呈周期性变化,钢球相对于内外摆线槽都不是纯滚动,只在有限点处相对速度为零。图6中,钢球与中心盘的相对速度矢vb1变化曲线在x、y方向上有两个波峰,分别出现在齿顶与齿根处。x方向的波峰滞后于y方向的波峰。在半齿高处出现两个小波峰,其值为齿顶处波峰值一半。在z方向上有两个波峰,一个波谷,其中两个波峰出现在半齿高处,为正值,波谷出现在齿顶处,为负值。图7中,钢球与行星盘的相对滑动速度矢vb2在x、y方向上较大,曲线有两个波峰分别出现在半齿高附近。 y方向上波峰较x方向上波峰出现得早。在z方向上,钢球与行星盘相对滑动速度较小,曲线有三个峰值,在齿根附近滑动速度绝对值最大,且为负值。 x、y方向上波峰值为 z方向上波峰值的7.7倍与7.9倍。由于槽形角 β=45°,vb1与 vb2在点 Aʹ、Bʹ和点 A、B 处差别不大。
4.2 槽形角对速度矢的影响
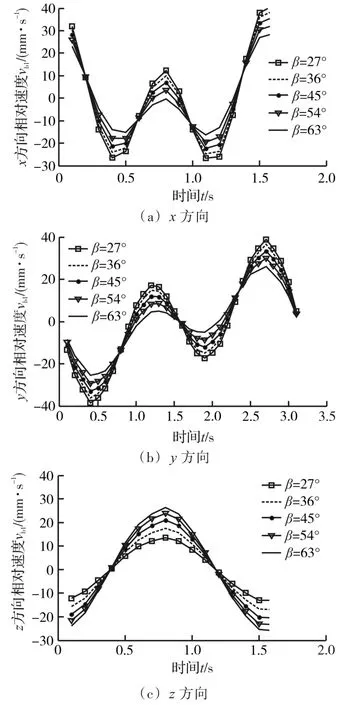
图8 槽形角在Bʹ点处对vb1的影响Fig.8 Influence of the groove angle on the relative velocityvb1at the pointBʹ
由图6、图7可知,钢球与中心盘和组合行星盘内外两侧的速度相差较小,所以以下只考虑摆线盘内侧情况。图8给出了槽形角分别为27°、36°、45°、54°、63°时,在 x、y 、z方向上钢球与中心盘的相对速度vb1。由于对称性,只讨论半个齿内的相对速度。在外摆线内侧,即Bʹ点处,x、y方向上随着槽形角的增大,vb1变化减小。相差最大点发生在半齿高处以及齿顶附近,Bʹ点处的差值分别为12.835 0 mm/s与13.035 2 mm/s,这是由于此处曲率变化最大。当 β=27°时,相对速度变化最大。z方向上随着槽形角的增大,相对速度变化增大。相差最大点发生在半齿高处,Bʹ点处的差值为7.906 7 mm/s。
图 9给出了槽形角分别为 27°、36°、45°、54°、63°时,在x、y、z方向上钢球与组合行星盘的相对速度vb2。由于对称性,只讨论在x、y方向半个齿以及z方向一个齿的相对速度。在内摆线内侧,即 A点处,在三个方向上,随着槽形角的增大,vb2变化增大。在x方向上,相差最大的点在齿顶处,为13.226 0 mm/s。在 y方向上,vb2相差最大的点在1/3齿高处,差值为16.039 7 mm/s。在z方向上,后半齿廓比前半齿廓变化较大,vb2相差最大的点在过齿顶1/3齿高处,差值为11.800 2 mm/s。当 β =63°时,vb2最大。

图9 槽形角在A点处对vb2的影响Fig.9 Influence of the groove angle on the relative velocityvb2at the pointA
4.3 钢球数对相对速度的影响
图10、图11分别给出了钢球数分别为10、15、20、25、30时,在 x、y、z方向上钢球与中心盘和组合行星盘的相对速度vb1和。由于运动周期不同,只讨论钢球数为30的一个周期内的相对速度。在x、y、z方向上,钢球滚过内外摆线槽一个齿所用的时间随着钢球数的增大而增多,分别为0.923 1 s、2.100 0 s、3.755 4 s、6.000 0 s、8.400 0 s和 0.466 7 s、1.100 0 s、1.900 0 s、3.328 3 s、4.200 0 s。钢球数对vb1的最大值与最小值影响不大,vb2的最大值随钢球数的增大而增大,最小值随钢球数的增大而减小。

图10 钢球数在Bʹ点处对vb1的影响Fig.10 Influence of the number of ball on the relative velocityvb1at the pointBʹ
5 仿真验证
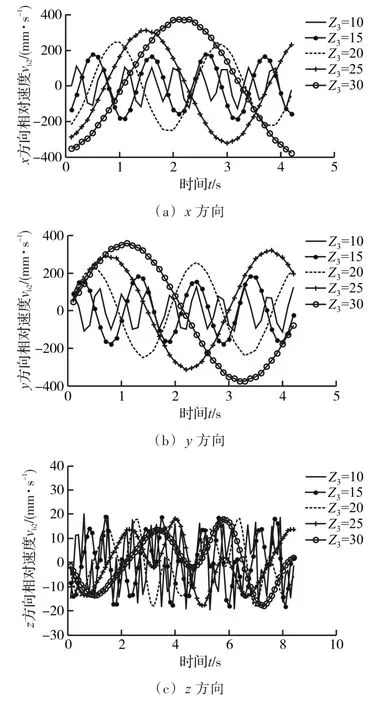
图11 钢球数在A点处对vb2的影响Fig.11 Influence of the number of ball on the relative velocityvb2at the pointA
根据图1所示的几何模型和上节数值模拟的几何参数,在ADAMS中建立减速部分几何模型,设置如下约束:①减速机构部件中,偏心输入轴、中心盘、组合行星盘、减速钢球系以及输出装置均采用钢材材质;②偏心输入轴与组合行星盘和中心盘,输出盘与机壳的约束均定义为旋转约束,中心盘与机壳为固定约束;③中心盘、组合行星盘与钢球之间定义接触力:刚度系数取值为1×105N/m,非线性系数取值为2.2,黏滞阻尼系数为10 N·s/m,最大阻尼切入深度取值为0.1 mm;④仿真时间取5 s,步长为 0.001 s。
图12为实时无隙钢球精密传动减速部分ADAMS仿真图。为了验证本文模型的正确性,将钢球与中心盘和组合行星盘的相对速度矢数值模拟结果与ADAMS仿真结果进行对比。图13为vb1、vb2的数值解与仿真解对比图。由图13a可知,x、y方向上,vb1的数值解与仿真解误差最大值分别为11.542 9 mm/s和10.504 1 mm/s,相对误差最大值分别为5.54%、4.51%。这是由于半齿高处有曲率半径奇异点,钢球转动时容易打滑。z方向上,误差值最大的点发生在齿顶。
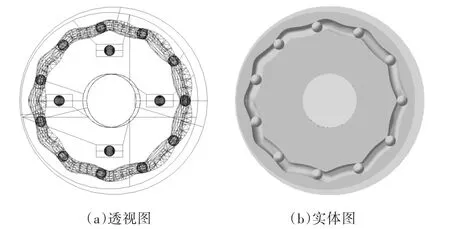
图12 ADAMS仿真模型图Fig.12 Graph of ADAMS model
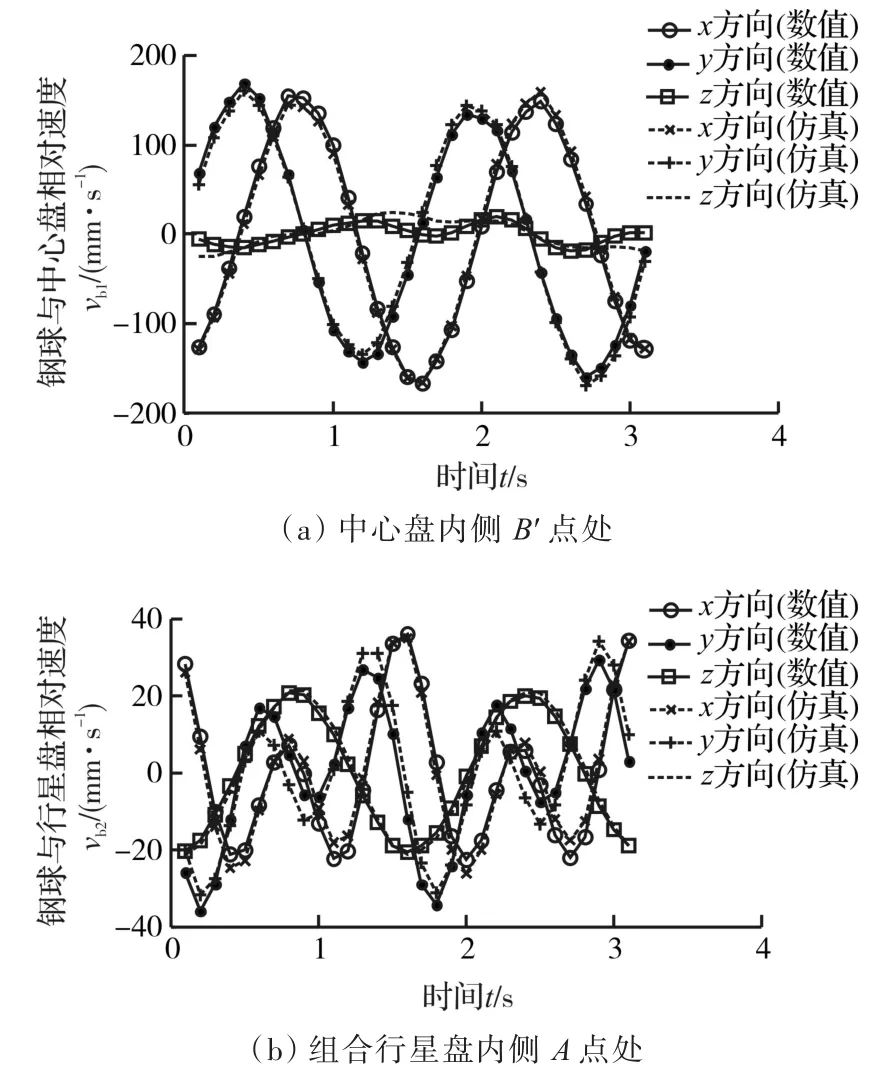
图13 钢球相对摆线盘速度对比图Fig.13 Comparison graph of velocity of steel ball relative to cycloid plates
由图13b可知,x、y方向上,vb2的数值解与仿真解误差最大值分别为4.213 3 mm/s和6.347 0 mm/s,相对误差最大值分别为5.54%和4.51%。 z方向上误差最大值为1.769 3 mm/s。最大误差发生在齿顶附近,这是由于钢球在齿顶处发生自旋。
本文推导了实时无隙钢球精密传动的空间速度矢模型,分析了机构参数对速度矢模型的影响,并将模型的数值解与ADAMS仿真解进行了对比分析。结果显示,两者有很好的一致性,验证了空间速度矢模型的正确性,为提高减速机构的精度提供了可靠的理论基础。
6 结论
(1)钢球与中心盘的相对速度矢vb1曲线在x、y方向上波峰出现在齿顶与齿根处,在z方向上两个波峰出现在半齿高处,波谷出现在齿顶处。钢球与组合行星盘相对速度矢vb2曲线在x、y方向上较大,曲线波峰分别出现半齿高附近,在z方向上波峰在齿根附近。x、y方向上波峰值为z方向上波峰值的7.7倍与7.9倍。
(2)在 x、y方向上,随槽形角增大,vb1变化幅值减小,在z方向上,变化幅值增大。在x、y、z方向上,vb2变化幅值随槽形角的增大而增大。钢球数对vb1影响不大,vb2的最大值随钢球数增大而增大,最小值随钢球数增大而减少。
(3)x、y方向上,vb1的数值解与仿真解相对误差最大值分别为5.54%和4.51%。vb2的数值解与仿真解相对误差最大值分别为2.89%和3.84%。
参考文献:
[1] 王国彪,赖一楠,范大鹏,等.新型精密传动机构设计与制造综述[J].中国机械工程,2010,21(16):1891-1897.
WANG Guobiao,LAI Yinan,FAN Dapeng,et al.Sum⁃mary of New Type Precision Transmission Design and Manufacture[J].China Mechanical Engineering,2010,21(16):1891-1897.
[2] HIDETSUGU T.The Development of Gearless Reduc⁃ers with Rolling Balls[J].Journal of Mechanical Sci⁃ence and Technology,2010,24:189-195.
[3] AN Zijun,YI Yali.Force Analysis and Stress Calcula⁃tion of Non-clearance Cycloid Ball Transmission[C]//Proceedings of IEEE International Conference on Me⁃chatronics and Automation. Takamatsu, 2008:1089-1093.
[4] 宜亚丽,安子军,王海侠.无隙钢球精密传动啮合副滑动特性研究[J].中国机械工程,2014,25(23):3206-3211.
YI Yali,AN Zijun,WANG Haixia.Research on Slid⁃ing Property of No-backlash Ball Precision Transmis⁃sion Meshing Pair[J].China Mechanical Engineering,2014,25(23):3206-3211.
[5] 张鹏,安子军,杨作梅.摆线钢球行星传动啮合副非线性力学性能研究[J].工程力学,2010,27(3):186-192.
ZHANG Peng,AN Zijun,YANG Zuomei.Research on Nonlinear Mechanical Properties for Engagement Pair of Cycloid Ball Planetary Transmission[J].Engineer⁃ing Mechanics,2010,27(3):186-192.
[6] 张鹏,安子军.摆线钢球行星传动动力学建模与固有特性分析[J].中国机械工程,2014,25(2):157-162.
ZHANG Peng,AN Zijun.Dynamics Model and Natural Characteristics of Cycloid Ball Planetary Transmission[J].China Mechanical Engineering,2014,25(2):157-162.
[7] 杨荣刚,安子军.基于谐波平衡法的摆线钢球行星传动等速输出机构非线性动态特性研究[J].振动与冲击,2017,36(2):153-158.
YANG Ronggang,AN Zijun.Nonlinear Dynamic Char⁃acteristics of the Equal Speed Output Mechanism of Cycloid Ball Planetary Transmission Based on Harmon⁃ic Balance Method[J].Journal of Vibration and Shock,2017,36(2):153-158.
[8] 孙鹏飞,安子军,刘向辉.精密钢球传动减速机构的瞬时接触热特性分析[J].中国机械工程,2017,28(9):1009-1015.
SUN Pengfei,AN Zijun,LIU Xianghui.Analysis on In⁃stantaneous Contact Thermal Characteristics of Reduc⁃ing Mechanisms for Precision Ball Transmissions[J].China MechanicalEngineering,2017,28 (9) :1009-1015.
[9] 甘屹,王均垒,孙福佳.基于给定工作空间的6R型机器人D-H参数优化设计[J].中国机械工程,2014,25(22):3003-3007.
GAN Yi,WANG Junlei,SUN Fujia.Optimal Design of D-H Parameters of a 6R Robot for a Prescribed Workspace[J].China Mechanical Engineering,2014,25(22):3003-3007.
[10] CONTE J,SANTOLARIA J,MAJARENA A C,et al.Laser Tracker Kinematic Error Model Formulation and Subsequent Verification under Real Working Conditions[J].Procedia Engineering,2015,132:788-795.
[11] LI Z,SCHICHO J.A Technique for Deriving Equa⁃tional Conditions on the Denavit-Hartenberg Parame⁃ters of 6R Linkages that Are Necessary for Movability[J].Mechanism&Machine Theory,2015,94:1-8.
[12] DUAN Liying,AN Zijun,YANG Ronggang,et al.Mechanical Model of Coupling Rolling and Sliding Friction in Real-time Non-clearance Precision Ball Transmission[J].Tribology International,2016,103:218-227.
[13] 吴序堂.齿轮啮合原理[M].北京:机械工业出版社,1982:145-163.WU Xutang.The Principle of Gear Engagement[M].Beijing:Mechanical Industry Press,1982:145-163.
(编辑 王艳丽)
作者简介:段利英,女,1982年生,博士研究生。主要研究方向为现代机械传动理论及应用。发表论文7篇。E-mail:duanly05@sina.com。安子军(通信作者),男,1960年生,教授、博士研究生导师。主要研究方向为现代机械传动理论与控制。发表论文120余篇。E-mail:zjan@ysu.edu.cn。
