双边拆卸线平衡问题建模与优化

邹宾森 张则强 李六柯 蔡 宁

西南交通大学机械工程学院，成都，610031

0 引言

在当今资源日益匮乏的背景下，产品回收再制造因其节能环保的优良特性，受到了世界各国的重视。近年来，国家相关机构出台了《再生资源回收体系建设中长期规划（2015～2020年）》等一系列政策法规，以推进再制造行业的良好发展，拆卸作为从资源回收到再利用中重要的一步，受到了国内外学者广泛的研究和关注。

为保证拆卸作业高效流畅地进行，当前规模化的拆卸主要采用拆卸线的作业形式，拆卸线具有效率高、节约生产空间等优点，但在拆卸作业中当任务在工作站内分配不合理时会带来拆卸线平衡问题（disassembly line balancing problem，DLBP）。

GUNGOR等［1］最先建立了多目标DLBP数学模型以优化拆卸生产线。结合实际生产情况，学者对DLBP模型进行了拓展和完善。针对实际拆卸作业中复杂的工况和不确定性，KALAYCI等［2］对模糊环境下的DLBP展开了研究。结合U形布局节约生产空间、减低物流输送成本的优点，AGRAWAL等［3］建立了U形布局的DLBP模型。KALAYCILAR等［4］建立了工作站数固定、节拍时间不定的DLBP数学模型，以体现待拆卸零件特定限制供应的工况。由于DLBP求解的复杂性，因而DLBP的求解方法成为学术研究重点。已有的DLBP求解方法包括变邻域搜索［5］、强化学习算法［6］、贪婪算法［7］等启发式方法，但因 DLBP 的NP-hard属性，上述算法针对大规模DLBP无法在合理的时间内求得理想的解。结合智能方法参数少、效率高的优点，粒子群算法［8］、遗传算法［9］和人工蜂群算法［10］等被广泛应用于求解DLBP，但这些方法均是将多目标DLBP转换为单目标问题进行求解，丧失了解的多样性。为保证多目标问题解的多样性，文献［11-12］分别提出了基于Pareto的蚁群算法和人工鱼群算法，一次运算能求得多种平衡方案，但其求解性能仍有待进一步提升。

对于大型或受作业方位约束的产品，若采用传统的单边作业形式，拆卸中作业产品需要频繁地调整方向，会产生大量的无效操作和降低生产效率，而采用双边作业形式能有效减少因作业方位约束导致的无用功［13-15］，从而提高作业效率、降低生产成本。

蝙蝠算法（bat algorithm，BA）［16］因具有算法参数少、收敛速度快和收敛精度高等优点［17］，一经提出便倍受关注，被广泛地应用于求解车间调度问题［18］、发电系统成本优化［19］以及其他多目标优化问题［20］，均取得了良好的求解结果，表明蝙蝠算法在求解离散问题及多目标问题上具有优良的求解性能。但目前尚未有将蝙蝠算法用于求解DLBP的公开报道，因此将蝙蝠算法应用于求解DLBP具有重要的研究价值。

本文对双边拆卸线平衡问题（two-sided disas⁃sembly line balancing problem，TDLBP）展开了研究，建立了多目标TDLBP数学模型。针对所建立的TDLBP数学模型，提出一种基于Pareto的蝙蝠算法进行求解。

1 双边拆卸线平衡问题

当前DLBP研究中，如图1所示，均假定工作站布置在输送带的同侧，尚未有双边拆卸线平衡问题的公开研究报道，但经实地调研后发现，双边拆卸被广泛地应用于实际拆卸作业中。图2为双边拆卸线示意图。

图1 单边拆卸线示意图Fig.1 The schematic diagram of the one-sided disassembly line

如图2所示，双边拆卸线中，工作站布置在输送带的左右两侧，在满足拆卸优先关系的前提下，左右两边可同时进行拆卸作业。按零部件的拆卸方位约束，将零部件分为L、R、E三类。其中标记L的任务只能在拆卸线左侧工作站内进行拆卸；标记R的任务只能在拆卸线右侧工作站内进行拆卸；标记E的任务在拆卸线左右两侧均可进行拆卸。

图2 双边拆卸线示意图Fig.2 The schematic diagram of the two-sided disassembly line

理论假设：①相同产品的同一零部件的拆卸时间固定且相同；②双边同时作业时互不干扰。

符号说明：N为开启的工作站数目；j为拆卸工作站编号；CT为拆卸生产节拍；STj为工作站 j的拆卸作业时间；l为分配至左侧工作站中的拆卸序列编号；r为分配至右侧工作站中的拆卸序列编号；nL为分配至左侧工作站的任务总数；nR为分配至右侧工作站的任务总数；为分配至左侧工作站的拆卸序列中第l处的拆卸任务；为分配至右侧工作站的拆卸序列中第r处的拆卸任务；dkL为任务的需求指数，若任务l拆卸的零部件定义为有需求零部件，根据零件的需求程度，dkL取大于零的整数，若任务拆卸l的零部件无需求价值，则为任务的危害指数，若任务klL拆卸的零部件定义为有害零部件，则hkL=1，否则 hkL=0；n为拆卸任务总数；li为拆卸任务编号；ti为任务i拆卸所需时间；WTj为工作站 j的等待时间；Ti为任务i的开始拆卸时刻；aiiʹ为任务优先关系，当任务i优先于任务iʹ时，则 aiiʹ=1，否则 aiiʹ=0 ；P 为任务优先关系矩阵，P=[aiiʹ]n×n；mi为任务 i的拆卸方位属性，当任务i只能在生产线左边拆卸时，mi={1}，当任务i只能在生产线右边拆卸时，mi={2}，任务i在生产线左右两侧均可拆卸时，mi={1，2}；zj为工作站 j的方位属性，当工作站 j布置在生产线左侧时，zj=1，当工作站 j布置在生产线右侧时，zj=2；eij为拆卸任务分配属性，当任务i被分配到工作站 j中且 zj∈mi时，eij=1，否则eij=0。

目标函数如下［6］：

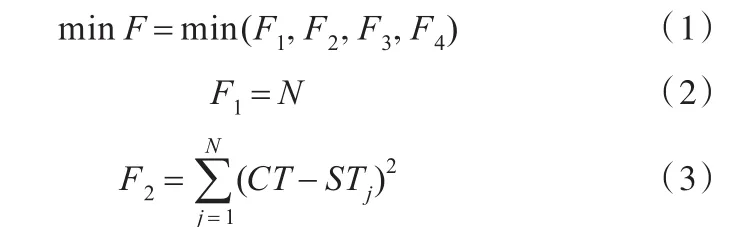
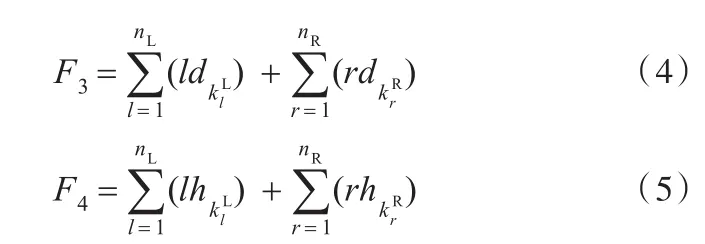
约束条件如下：作站数目和最大工作站数目n之间。式（7）约束工作站作业时间与等待时间之和不超过生产节拍。式（8）确保拆卸满足优先关系。式（9）确保每一个零件均被拆卸且只能被分配在一个工作站内进行拆卸。

式（2）为开启的工作站数目，为降低拆卸成本，应最小化开启的工作站数目。式（3）为拆卸线空闲时间指标，为使工作站闲置时间最短和提高拆卸效率，应最小化拆卸空闲时间指标。式（4）为拆卸需求指标，为尽可能早地拆卸需求价值高的零件，应最小化拆卸需求指标。式（5）为拆卸危害指标，为尽可能降低有害零部件在拆卸过程中对环境的污染和对工人健康的损害，应最小化拆卸危害指标。式（6）约束实际开启工作站数目介于最小工

2 Pareto蝙蝠算法

2.1 编码

基于DLBP特性，本文采用拆卸序列进行编码。为保证算法能在尽可能大的空间内进行搜索寻优以及避免人为因素对初始种群的影响，采用随机产生的满足优先关系的拆卸序列作为初始种群。以包含5个任务的算例为例简述初始种群个体的产生过程，该算例任务优先关系如图3所示。初始，可选任务集为｛1｝，因此选任务1为第一个拆卸任务，解除任务1的紧前性质，可选任务集更新为｛2，5，3｝；随机选取任务5作为第二个拆卸任务，解除任务5的紧前性质，可选任务集更新为｛2，3｝；随机选取任务2作为第三个任务，解除任务2的紧前性质，可选任务集合更新为｛3，4｝；随机选取任务4作为第四个拆卸任务；最后剩下的任务3作为第五个拆卸任务，得到一个初始个体即拆卸序列为｛1，5，2，4，3｝。

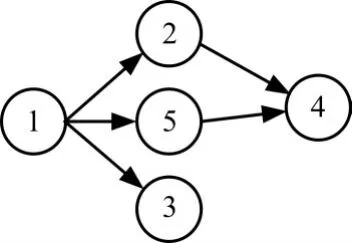
图3 算例优先关系图Fig.3 The precedence diagram of the example

2.2 蝙蝠算法

借鉴蝙蝠精准的捕食行为，将算法寻优过程模拟为蝙蝠捕食过程。将猎物模拟为解空间中的可行解，将搜索和寻优过程中用适应度高的解替代适应度低的解的迭代过程，类比为个体的优胜劣汰过程。

蝙蝠算法中，当rand1≤sq时，蝙蝠算法采用速度-位置模型对个体进行更新，其中，rand1为［0，1］之间的随机数，sq为第q只蝙蝠个体的脉冲频度。

速度更新：

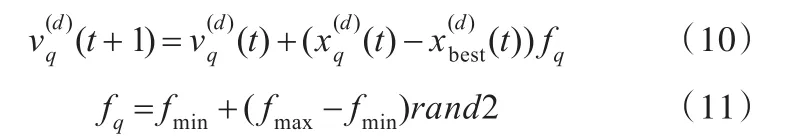
式中，(t+1)为第t+1次迭代中第q只蝙蝠的第d位的速度分量；(t)为第q只蝙蝠的第d位的位置分量；为当前最优位置的第d位位置分量；f为第q个q个体的脉冲频率；fmin、fmax分别为脉冲频率的最小值和最大值；rand2为［0，1］之间的随机数。

拆卸线平衡问题是一个离散问题，因此将蝙蝠算法应用于求解拆卸线平衡问题时需将算法离散化。考虑拆卸线平衡问题采用拆卸序列编码的特性，定义位置之差为两个解对应序列位置的不同任务的任务数组。如若 x1(t)=｛1，3，2，5，4｝、x2(t)=｛3，5，2，4，1｝，则可知、=3，则=｛1，3｝，每相减一次将 x2(t)中的对应拆卸任务交换位置以更新x2(t)，即可知x1(t)-x2(t)=｛1，3，2，5，4｝-｛1，5，2，4，3｝+｛｛1，3｝｝=｛1，3，2，5，4｝-｛1，3，2，4，5｝+｛｛1，3｝，｛3，5｝｝=｛1，3，2，5，4｝-｛1，3，2，5，4｝+｛｛1，3｝，｛3，5｝，｛4，5｝｝=｛｛1，3｝，｛3，5｝，｛4，5｝｝=v 。定义 fq为(xq(t)-xbest(t))中实际参与速度更新的长度比例：若 vq(t)=｛｛1，2｝｝，(xq(t)-xbest(t))=｛｛2，3｝，｛3，4｝，｛4，5｝｝，fq=0.5，因｛｛2，3｝，｛3，4｝，｛4，5｝｝长度为3，则(xq(t)-xbest(t))中实际参与速度更新的对数为对，随机取两组｛｛2，3｝，｛3，4｝｝，则 vq(t+1)=vq(t)+(xq(t)-xbest(t))fq=｛｛1，2｝｝+｛｛2，3｝，｛3，4｝｝=｛｛1，2｝，｛2，3｝，｛3，4｝｝。

位置更新：

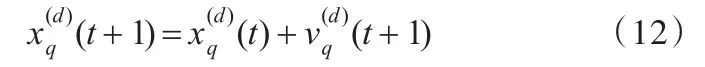
定义位置与速度相加为对原拆卸序列中的任务按速度数组进行交换。如若 x2(t)=｛3，5，2，4，1｝、v=｛｛1，3｝，｛3，5｝，｛4，5｝｝，x2(t)与速度 v 中速度分量｛｛1，3｝｝相加表示将 x2(t)中任务1和任务3的位置互换，则 x2(t)+v=｛3，5，2，4，1｝+｛｛1，3｝，｛3，5｝，｛4，5｝｝=｛1，5，2，4，3｝+｛｛3，5｝，｛4，5｝｝=｛1，3，2，4，5｝+｛｛4，5｝｝=｛1，3，2，5，4｝。

蝙蝠算法中，当rand1＞sq时，在当前全局最优附近进行随机搜索以寻找新的位置。鉴于拆卸线中优先关系的存在，本文采用如下方式对当前全局最优进行随机搜索：从全局最优中随机选择一个任务，将所选任务随机插入到最近的紧前任务和最近的紧后任务之间，完成局部搜索。局部搜索如图4所示。

图4 局部搜索示意图Fig.4 The schematic diagram of the loach search

蝙蝠算法中，当个体新位置优于原位置则接受新位置；若个体新位置劣于原位置且rand3＜Aq时，接受新位置以避免算法陷入局部最优，其中rand3为［0，1］之间随机数，Aq为第q只蝙蝠个体的脉冲音强。较小的脉冲音强能保证接受劣于当前位置的新位置的概率越来越小。为更精准地掌握目标位置，随着算法的不断进行，当个体更新后优于当前全局最优时，采用下式不断增大脉冲频度sq和减小脉冲音强Aq：

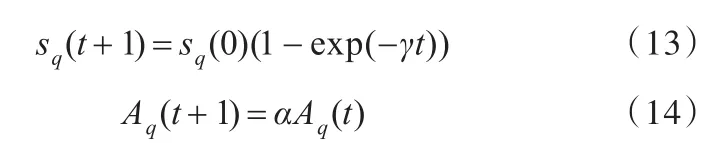
式中，sq(0)为初始脉冲频度；γ为脉冲频度增加系数，一般为一个大于零的常数；α为脉冲音强衰减系数。

2.3 解码方式

TDLBP中，解的产生还需要对可行拆卸序列进行解码，为缩短工件在输送带上的输送路径以及使工作站内空闲时间最短，本文在解码中对于不受拆卸方位约束的任务优先分配至开启工作站较少的一边，当两边工作站开启数目相同时，优先将任务分配至空闲时间较多的工作站内。具体解码方式如图5所示。其中，jL为左侧当前开启的工作站编号；jR为右侧当前开启的工作站编号；RjL为工作站 jL的剩余时间。

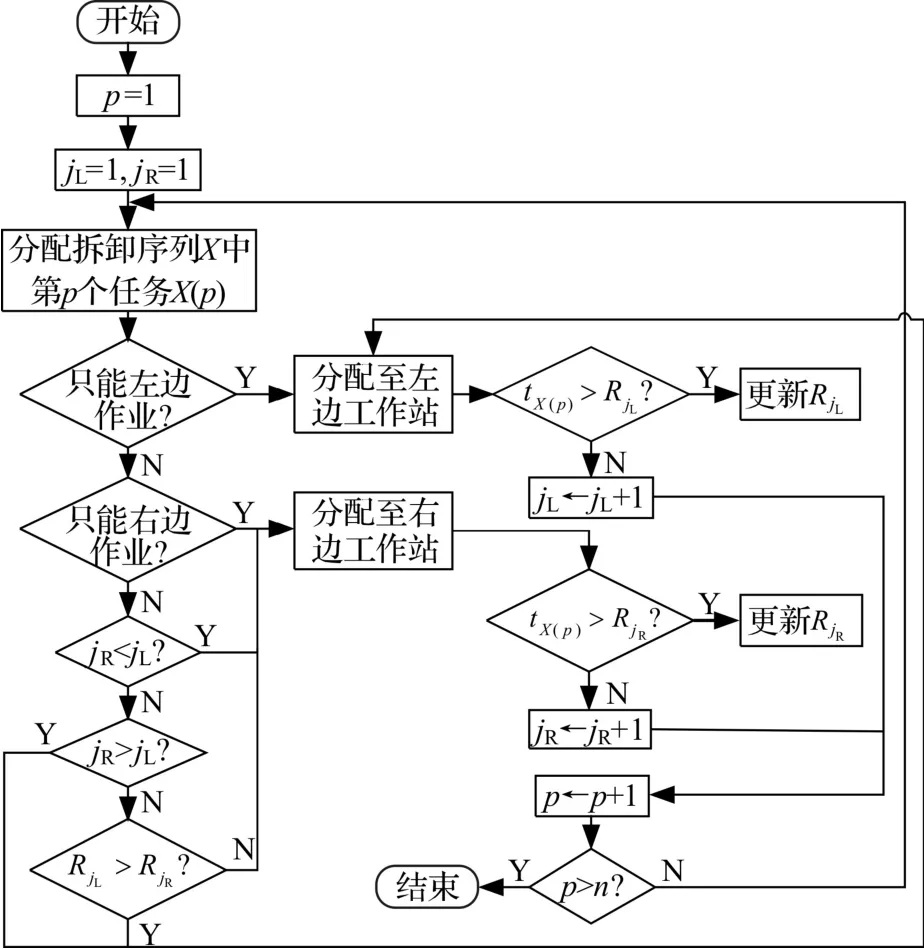
图5 解码方式Fig.5 The decoding method

2.4 Pareto非劣解

若最小化多目标问题中可行解u和uʹ满足：

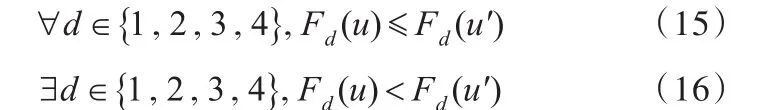
则称 uPareto支配 uʹ，记为 u≺uʹ。如 F(u)=｛6，20，15，4｝，F(uʹ)=｛7，20，26，6｝，因对于 ∀d ∈{1，2，3，4}， Fd(u)≤Fd(uʹ) 均 成 立 ；且 当 d=1 时 ，Fd(u)=6，Fd(uʹ)=7，Fd(u)＜ Fd(uʹ)成立，因此可知u≺uʹ。解空间中不被支配的解称为Pareto最优解或非劣解，所有非劣解组成的集合称为Pare⁃to最优解集，对应的目标函数值称为Pareto最优前沿。

2.5 外部档案更新

算法每迭代完成一次，将外部档案中非劣解与当前种群进行一次Pareto比较，筛选出两者合集的非劣解保存至外部档案中，以确保外部档案中的非劣解始终为当前全局非劣解。如外部档案Q={x3，x4}，当前种群 X={x5，x6}，其中 x3、x4互不支配，x5支配 x4、x6，且 x5与 x3互不支配。外部档案和当前种群合集为 {x3，x4，x5，x6}，则可知外部档案和当前种群合集的非劣解集为{x3，x5}，因此外部档案 Q 更新为{x3，x5}。

多目标问题的解是多个互不占优的非劣解，规模往往较大，但外部档案规模过大则会降低算法运行速度。为提高算法运行效率和让更具代表性的非劣解参与寻优以加强算法寻优能力，当外部档案大小超过设定规模时需对外部档案进行筛选，本文采用基于拥挤距离的外部档案筛选方式［21］，依次剔除拥挤距离小的个体，直到外部档案大小等于设定规模。采用精英策略，用外部档案中的非劣解替换当前种群中的部分个体参与算法迭代寻优，加速算法的收敛。

2.6 算法步骤

（1）算法初始化：种群规模M ，脉冲频率搜索范围 fmin、fmax，最大脉冲频度s，最大脉冲音强 A，脉冲频度增加系数γ，脉冲音强衰减系数α，算法最大迭代次数gmax，外部档案规模 fN。

（2）算法当前迭代次数Tc=1。

（3）外部档案集初始化，令外部档案集为空集。

（4）种群初始化。

（5）若rand 1＞sq，则对当前最优个体产生一个随机扰动，产生新个体 xnew；否则采用式（12）产生新个体xnew。

（6）若新个体优于原个体，则用新个体替换原个体，转至步骤（8）；否则转至下一步。

（7）若rand 3＜Aq，则用新个体替换原个体。

（8）若更新后个体优于当前全局最优，则更新 Aq和sq；否则转至下一步。

（9）更新外部档案。

（10）

（11）若Tc＞gmax，则执行下一步；否则转至步骤（5）。

（12）输出外部档案集。

（13）算法结束。

蝙蝠算法流程如图6所示。

图6 蝙蝠算法流程图Fig.6 The flow diagram of BA

3 算法验证与实例应用

为验证算法的有效性，将模型应用于实际拆卸线规划中，本文在配置为 Inter（R）Core（TM）i3-2100 CPU@3.10GHz，4.00GB内存的计算机上，在Win7系统下采用MATLAB R2014b开发了所提生算法的实验程序。

3.1 算法验证

已有的多目标DLBP研究中，尚无双边布局的模型实例，因此无法通过求解双边拆卸模型验证算法的有效性。但已有的直线形DLBP是双边布局中某一边开启的工作站数目为0的一种特殊情况，与TDLBP相比，只在于解码方式的不同，不会影响算法的结构进而不会影响算法的求解性能，因此通过求解直线形DLBP验证所提算法的有效性是可行的。

为验证算法的有效性，将蝙蝠算法应用于求解移动电话机拆卸实例［8］，该算例包含25个拆卸任务（以下简称“P25”），其中生产节拍CT=18，优化目标为 min(F1，F2，F3，F4)，该算例任务作业时间和任务优先关系图详见文献［8］。该算例的已有求解方法包括遗传算法（GA）［9］、模拟退火算法（SA）［22］、粒子群优化算法（PSO）［8］、强化学习算法（RL）［6］、变邻域搜索（VNS）［5］以及人工鱼群算法（AFSA）［12］。上述6种算法求解结果如表1所示。

表1 6种算法对P25求解结果Tab.1 The solutions of P25 of six algorithms

为保证算法最大的求解效率和最好的求解性能，经多次测试对比后，蝙蝠算法参数设置如下：种群规模M=180，脉冲频率搜索范围 fmin=0，fmax=1.2，最大脉冲频度s=0.6，最大脉冲音强A=0.85，脉冲频度增加系数γ=0.03，脉冲音强衰减系数α=0.9，算法最大迭代次数 gmax=200，外部档案规模 fN=8，算法运行30次，平均每次运行时间为34.956 s，其中一次运行结果如表2所示。

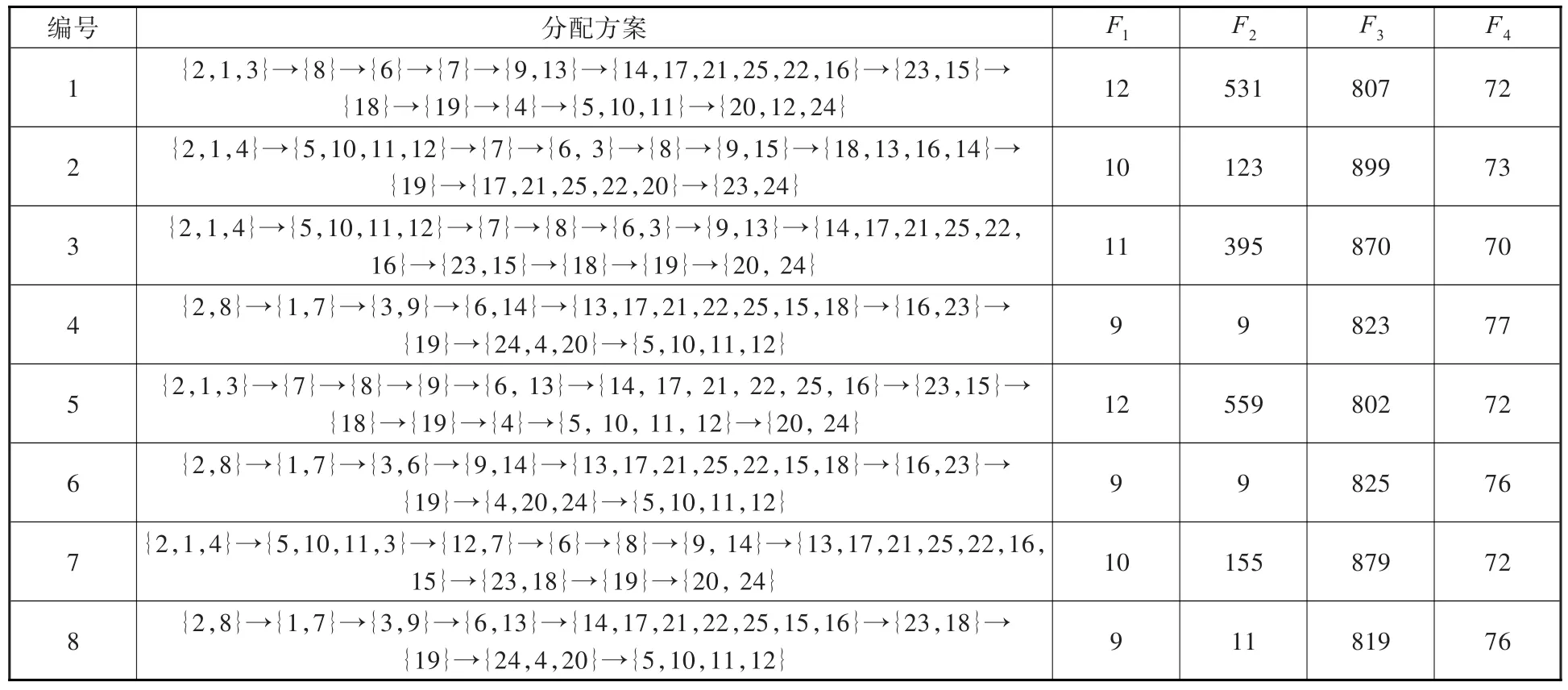
表2 蝙蝠算法对P25求解结果Tab.2 The solutions of P25 of bat algorithms

对比分析表1和表2可知，方案4和方案6完全优于GA、SA、PSO、RL的求解结果，方案1～方案3、方案5、方案7和方案8与上述4种算法求解结果互不占优，但上述4种算法没有一种求解结果优于本文算法；因此可知本文算法优于上述4种算法。VNS求解结果与方案6相同，与其余7种方案互不占优，但本文算法一次能求得多种平衡方案，同时 F3指标上能求得更优的 807、823、802、819，在F4指标能求得更优的 70、72、73；因此可知本文算法优于VNS。本文算法一次运算能求得多种平衡方案，且在F3指标和F4指标能求得更优异的值。

文献［12］采用人工鱼群算法对P25进行了求解，一次求得了8个平衡方案，对比蝙蝠算法求解结果和AFSA求解结果。AFSA所求得前两个平衡方案与本文所求得的方案6和方案4相同，其余方案与本文所求方案都互不占优。对比单个目标的求解结果可知，本文在F3指标上所求得的最小值为802，优于AFSA所求得的最小值809；本文在F4指标上所求得的最小值为70，优于AFSA所求得的最小值72。由此可知虽两种算法求解结果互不占优，但是本文算法在F3指标和F4指标上能求得更优的值，能为决策者在F3指标和F4指标上提供更优良的参考，即可知本文所提算法优于AFSA。通过上述对比，验证了本文所提算法的有效性。

3.2 实例应用

采用某公司某型号电冰箱拆卸作为求解算例以验证本文所提出模型和算法实际应用情况。针对该型号电冰箱拆卸流水线，采用多次秒表测量并取整的方式，得到表3中各任务作业时间，结合该型号电冰箱材料属性与市场需求，制订了各任务的需求和危害指标。结合实际生产情况，给定生产节拍CT=130 s。

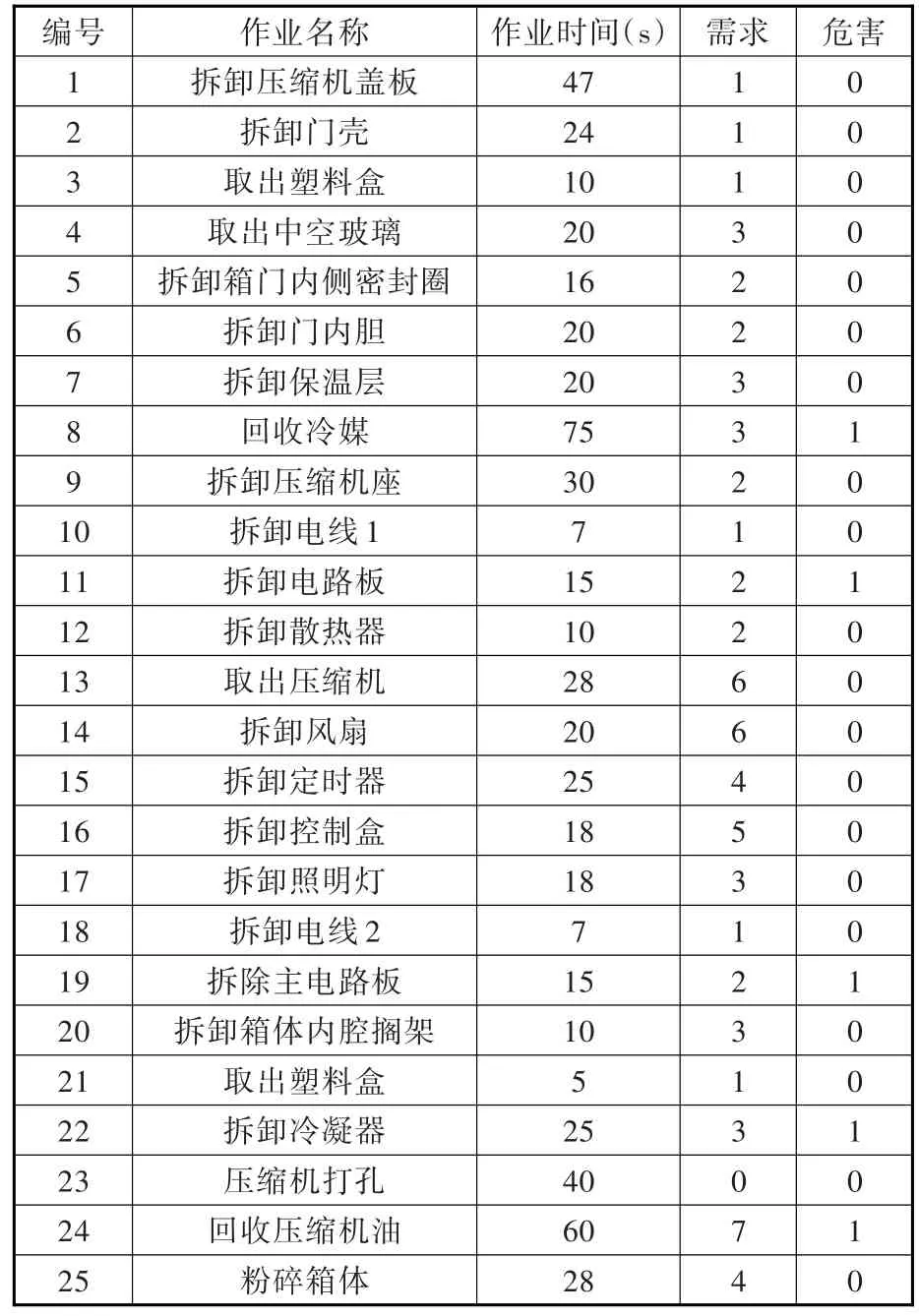
表3 冰箱拆卸信息表Tab.3 The information of the refrigerator disassembly

经多次观察与记录，制订了如图7所示的零件优先关系图，结合该型号电冰箱零部件的位置与构造，在零部件编号右上方给出了该零件的拆卸方位。

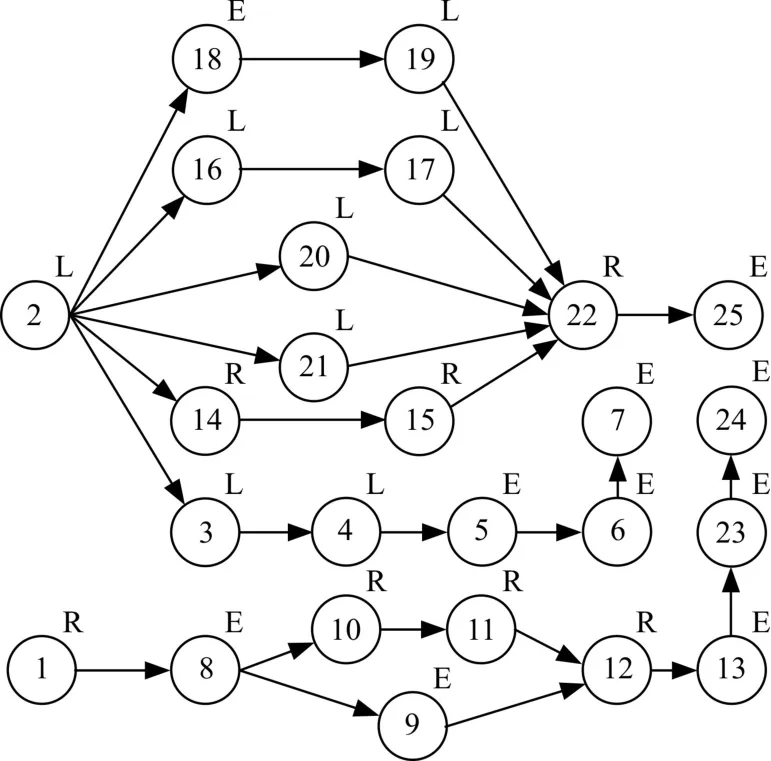
图7 冰箱拆卸优先关系图Fig.7 The precedence diagram of the refrigerator

针对该电冰箱拆卸实例，综合求解时间与求解效率，经多次参数设置比较，设定算法参数如下：种群规模M=200，脉冲频率搜索范围 fmin=0，fmax=1.2，最大脉冲频度s=0.55，最大脉冲音强 A=0.9，脉冲频度增加系数γ=0.04，脉冲音强衰减系数α=0.91，算法最大迭代次数 gmax=220，外部档案规模 fN=8，算法运行30次，平均每次运行时间为93.431 s，其中一次运行结果如表4所示，因拆卸线上任务时间之和、生产节拍固定，因此平衡率与开启的工作站数目成反比。

表4中，LW表示在左侧开启的工作站，RW表示在右侧开启的工作站。方案4中右侧第2个工作站未有任务分配，因此关闭该工作站以节约拆卸成本。由表4数据可知，针对包含25个任务的电冰箱双边拆卸实例，本文算法能一次求得多样化的分配方案。开启的工作站数目介于6和9之间，能为决策者提供多样的工作站数目决策；空闲时间指标包含介于5 907和51 679之间的不重复的8个值，保证需求指标质量的同时，危害指标也具有良好的分布性。当决策者注重F1指标时，可以选择方案1～方案3；当决策者注重F2指标时，可以选择方案1；当决策者注重F3指标时，可以选择方案7；当决策者注重F4指标时，可以选择方案6，综合决策时，可以从方案1～方案8之间挑选适合当前实际条件的平衡方案，为拆卸线的设计提供了一定的参考。

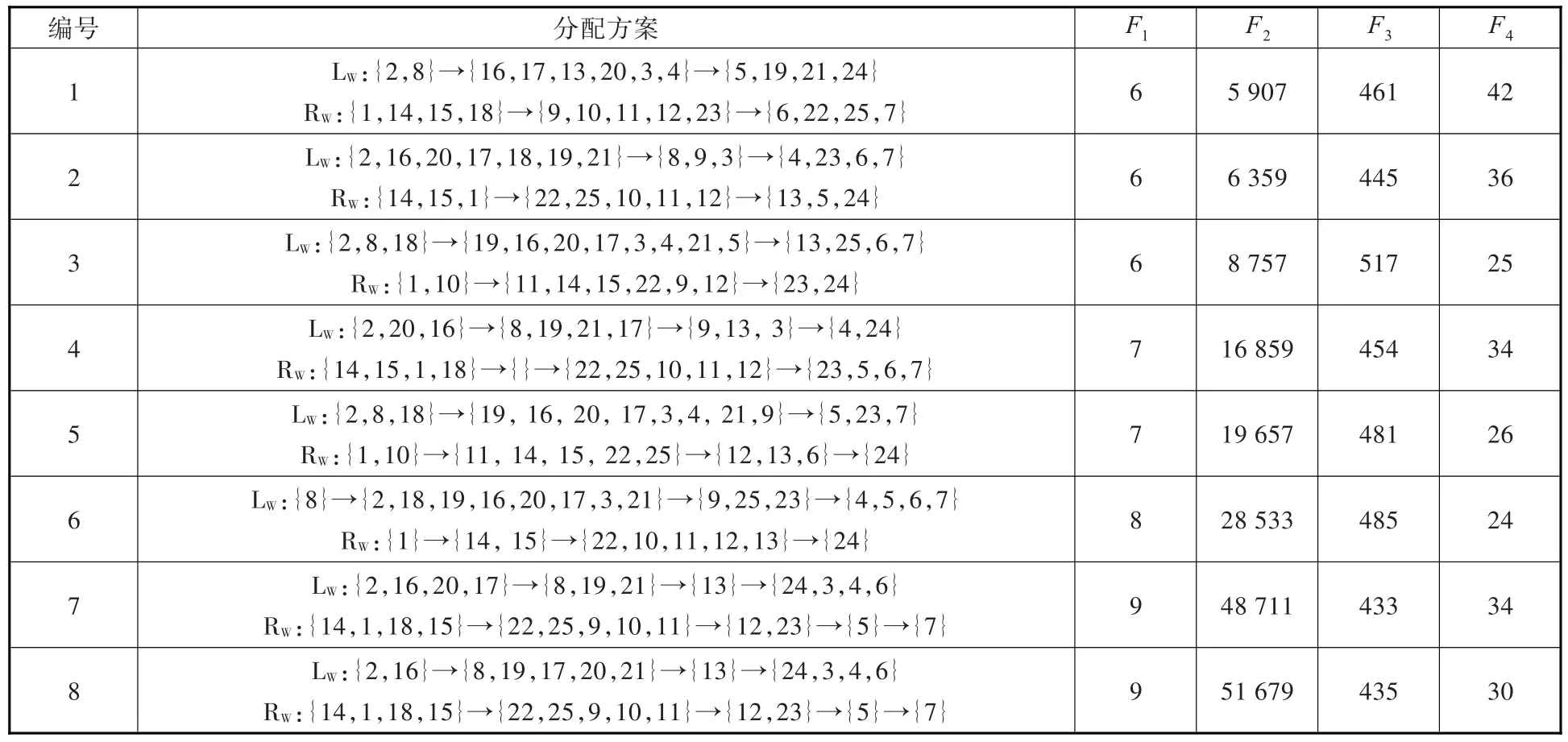
表4 电冰箱平衡分配方案Tab.4 The balancing allocation scheme of the refrigerator

为更好地展示任务分配结果，以方案1为例，列出具体分配方案示意图，见图8，其中LW1表示拆卸线左边开启的第一个工作站，RW1表示拆卸线上右边开启的第一个工作站。

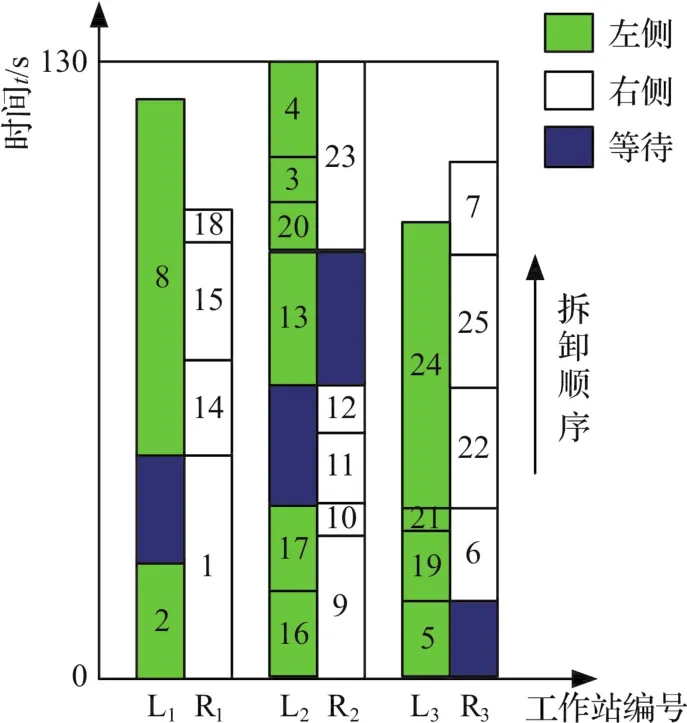
图8 方案1任务分配图Fig.8 The distribution of the scheme 1

4 结论

（1）根据拆卸方向，定义了零部件拆卸方位属性，首次采用双边拆卸，并建立了双边拆卸线平衡问题数学模型。解码中，任务优先分配到工作站开启较少的一边，缩短了工件输送路径，降低了拆卸成本；任务次优先分配至空闲时间较多的工作站，提高了拆卸效率。

（2）将Pareto思想引入蝙蝠算法，保留了解的多样性。引入精英策略将外部档案集作为部分种群参与迭代，有效加速了算法的收敛。采用拥挤距离精简外部档案，提高了算法的运行效率。

（3）求解包含25个任务的经典算例，并与已有的智能方法求解结果进行对比，验证了所提算法的有效性。将所建立模型和所提算法应用于电冰箱拆卸线设计研究中，能为决策者提供8种高质量的拆卸方案。

参考文献：

［1］ GUNGOR A，GUPTA S M，POCHAMPALLY K，et al.Complications in Disassembly Line Balancing［C］//1st InternationalConference on Environmentally Con⁃scious Manufacturing.Bellingham，WA：SPIE，2001：289-298.

［2］ KALAYCI C B，HANCILAR A，GUNGOR A，et al.Multi-objective Fuzzy Disassembly Line Balancing Us⁃ing a Hybrid Discrete Artificial Bee Colony Algorithm［J］.Journal of Manufacturing Systems，2014，37：672-682.

［3］ AGRAWAL S，TIWARI M K.A Collaborative Ant Col⁃ony Algorithm to Stochastic Mixed-model U-shaped Disassembly Line Balancing and Sequencing Problem［J］.International Journal of Production Research，2008，46（6）：1405-1429.

［4］ KALAYCILAR E G，AZIZOLU M，YERALAN S.A Disassembly Line Balancing Problem with Fixed Num⁃ber of Workstations［J］.European Journal of Operation⁃al Research，2016，249（2）：592-604.

［5］ KALAYCI C B，POLAT O，GUPTA S M.A Variable Neighborhood Search Algorithm for Disassembly Lines［J］.Journal of Manufacturing Technology Manage⁃ment，2015，26（2）：182-194.

［6］ TUNCEL E，ZEID A，KAMARTHI S.Solving Large Scale Disassembly Line Balancing Problem with Uncer⁃tainty Using Reinforcement Learning［J］.Journal of In⁃telligent Manufacturing，2014，25（4）：647-659.

［7］ MCGOVERN S M，GUPTA S M.Greedy Algorithm for Disassembly Line Scheduling［C］//IEEE International Conference on Systems，Man and Cybernetics.Piscat⁃away，NJ：IEEE，2003：1737-1744.

［8］ KALAYCI C B，GUPTA S M.A Particle Swarm Optimi⁃zation Algorithm for Solving Disassembly Line Balanc⁃ing Problem［C］//Proceedings of Northeast Decision Sciences Institute 2012 Annual Conference.Newport，Rhode Island，2012：347-357.

［9］ KALAYCI C B，POLAT O，GUPTA S M.A Hybrid Ge⁃netic Algorithm for Sequence-dependent Disassembly Line Balancing Problem［J］.Annals of Operations Re⁃search，2016，242（2）：321-354.

［10］ 张则强，胡扬，陈冲.求解拆卸线平衡问题的改进人工蜂群算法［J］.西南交通大学学报，2016，51（5）：910-917.ZHANG Zeqiang，HU Yang，CHEN Chong.Improved Artificial Bee Colony Algorithm for Disassembly Line Balancing Problem［J］.Journal of Southwest Jiaotong University，2016，51（5）：910-917.

［11］ DING L P，FENG Y X，TAN J R，et al.A New Multi-objective Ant Colony Algorithm for Solving the Disassembly Line Balancing Problem［J］.The Inter⁃national Journal of Advanced Manufacturing Technol⁃ogy，2010，48（5）：761-771.

［12］ 汪开普，张则强，毛丽丽，等.多目标拆卸线平衡问题的Pareto人工鱼群算法［J］.中国机械工程，2017，28（2）：183-190.WANG Kaipu，ZHANG Zeqiang，MAO Lili，et al.Pa⁃reto Artificial Fish Swarm Algorithm for Multi-objec⁃tive Disassembly Line Balancing Problems［J］.China Mechanical Engineering，2017，28（2）：183-190.

［13］ DELICE Y，AYDOAN E K，ÖZCAN U，et al.A Mod⁃ified Particle Swarm Optimization Algorithm to Mixed-model Two-sided Assembly Line Balancing［J］.Journal of Intelligent Manufacturing，2017，28（1）：23-36.

［14］ TANG Q H，LI Z X，ZHANG L P.An Effective Dis⁃crete Artificial Bee Colony Algorithm with Idle Time Reduction Techniques for Two-sided Assembly Line Balancing Problem of Type-Ⅱ［J］.Computers&In⁃dustrial Engineering，2016，97：146-156.

［15］ SEPAHI A，NAINI S G J.Two-sided Assembly Line Balancing Problem with Parallel Performance Capaci⁃ty［J］.Applied Mathematical Modelling，2016，40（13/14）：6280-6292.

［16］ YANG X S.A New Metaheuristic Bat-inspired Algo⁃rithm［J］.Computer Knowledge&Technology，2010，284：65-74.

［17］ YANG X S，GANDOMI A H.Bat Algorithm：a Novel Approach for Global Engineering Optimization［J］.Engineering Computations，2012，29（5）：464-483.

［18］ 徐华，张庭.混合离散蝙蝠算法求解多目标柔性作业车间调度［J］.机械工程学报，2016，52（18）：201-212.

XU Hua，ZHANG Ting.Hybrid Discrete Bat Algo⁃rithm for Solving the Multi-objective Flexible Job Shop Scheduling Problem［J］.Journal of Mechanical Engineering，2016，52（18）：201-212.

［19］ HEMALATHA S，CHANDRAMOHAN S.Cost Opti⁃mization of Power Generation Systems Using Bat Al⁃gorithm for Remote Health Facilities［J］.Journal of Medical Imaging and Health Informatics，2016，6（7）：1646-1651.

［20］ THARAKESHWAR T K，SEETHARAMU K N，PRASAD B D.Multi-objective Optimization Using Bat Algorithm for Shell and Tube Heat Exchangers［J］.Applied ThermalEngineering，2017，110：1029-1038.

［21］ DEB K，PRATAP A，AGARWAL S，et al.A Fast and Elitist Multiobjective Genetic Algorithm：NSGA-Ⅱ［J］.IEEE Transactions on Evolutionary Computa⁃tion，2002，6（2）：182-197.

［22］ KALAYCI C B，GUPTA S M.Simulated Annealing Algorithm for Solving Sequence-dependent Disassem⁃bly Line Balancing Problem［J］.IFAC Proceedings Volumes，2013，46（9）：93-98.

（编辑 袁兴玲）

作者简介：邹宾森，男，1990年生，硕士研究生。研究方向为生产线平衡与智能优化。张则强（通信作者），男，1978年生，教授、博士研究生导师。研究方向为制造系统与智能优化。E-mail：zzq_22@163.com。