车身动态刚度链建模及正向概念设计研究

胡裕菲 刘子建 钟浩龙 秦 欢

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

0 引言

正向开发是自主品牌汽车实现技术创新的必然途径，企业只有通过正向开发才能构建自己的研发体系、开发平台和流程体系。近年来，正向设计方法的研究越来越得到重视，如何在车身的概念设计阶段有效贯彻动态性能主导的原则，获得整体最佳的车身结构设计方案，仍然是车身设计方法领域有待探讨的重要问题。

ZUO等［1-2］在对车身主断面进行尺寸优化时，引入动态频率刚度作为约束条件，提出综合考虑振动特性进行车身动态设计的方法；ZIMMER等［3］考虑车身概念设计阶段设计自由度大的特点，为有效分析和整合标杆车的设计参数，提出了基于冲击和振动的隐式参数车身动态分析模型；王磊等［4］以轻量化为目标，综合考虑整车模态、弯扭刚度及碰撞安全性进行了车身正向开发；QIN等［5］利用分布式并行优化方法，针对车身正向设计开发了面向对象的MATLAB工具箱，便于主断面参数快速优化求解；刘子建等［6-7］针对车身结构概念设计提出了刚度链设计方法，在多种静态工况下，通过建立以主断面、接头等为节点的车身刚度链模型，对车身骨架进行刚度优化和轻量化设计，并指出综合考虑车身动态特性的刚度链设计方法还有待进一步研究。

本文在提出车身正向概念设计流程的基础上，建立了车身动态刚度链数学模型，分析了车身静刚度、振动特性与轻量化设计的关系，建立了车身设计优化模型，采用遗传算法求解了车身各主断面的属性，并通过对应标杆车的仿真分析结果验证了研究方法的可行性。

1 车身简化几何模型建模

汽车车身概念设计以冻结的油泥模型及总布置方案为起点，以主断面、接头、白车身、车门等设计结果和三维结构模型为终点，是车身结构设计的前期阶段，进行汽车车身概念设计的目的是为车身的详细设计提供结构可行的方案［8］。清晰合理的概念设计流程是完成性能主导的车身正向研发工作的重要保证，本文在深入研究刚度链设计方法特点和车身动态性能分析需求的基础上提出车身正向概念设计流程，如图1所示。

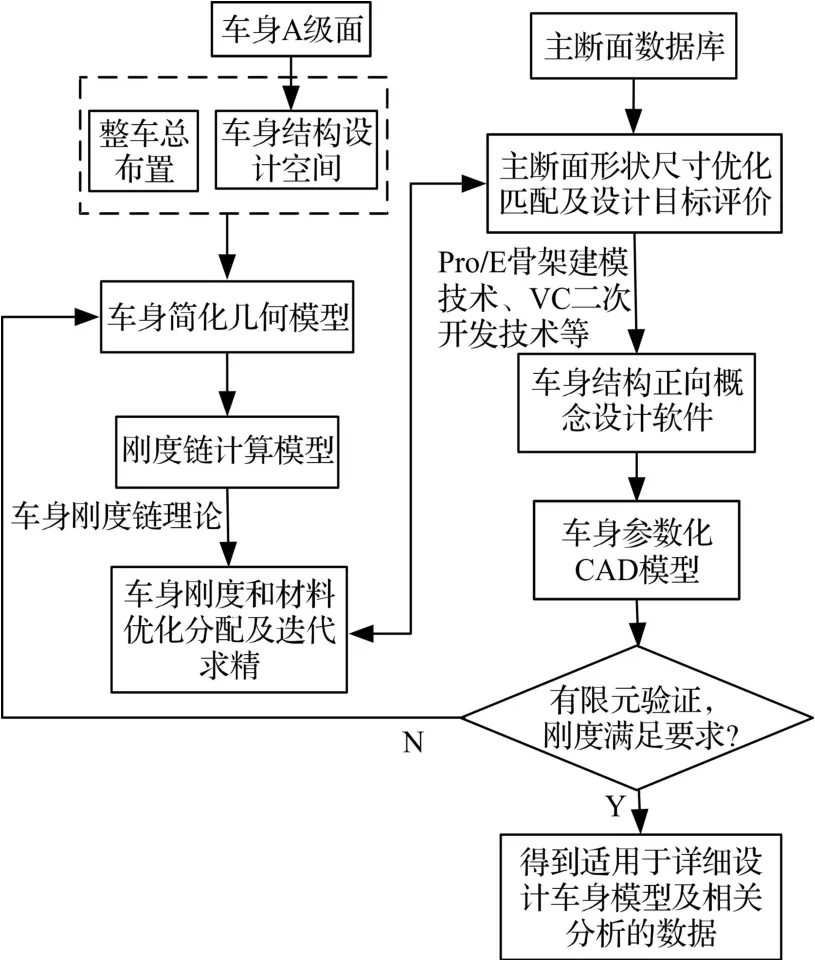
图1 车身正向概念设计流程Fig.1 The forward conceptual design process of vehicle body

依照上述流程，以某款A级乘用车为研究对象，其车身A级面与整车总布置方案如图2和图3所示。根据车身A级面及整车总布置方案得到车身初始框架结构，在此基础上，遵循特征点采集原则［9］，对点云数据进行处理，修正噪声点并减少冗余数据。对采集的特征点处理方法如下：①在全局坐标系中记录每个特征点的坐标数据；②依据车身形状有序采集数据及特征点的拓扑关系；③为方便后期数据处理，将某些数据进行坐标变换；④剔除异常点，对数据进行除噪、滤波和精简，增强数据的有效性和合理性；⑤提取控制几何形状的特征点，用于后续建模区域划分。

图2 车身A级面Fig.2 Class A surface of vehicle body

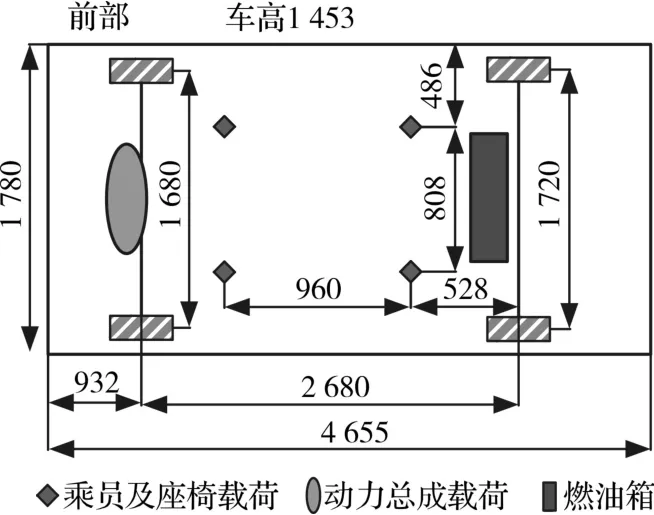
图3 整车总布置方案Fig.3 The scheme of vehicle general layout

根据乘用车车身顶盖系统、左侧围系统、右侧围系统、地板系统几大部分，建立梁单元表示的车身简化几何模型，如图4所示。在图4中，以前轴中心点为原点，X轴水平向后，Z轴竖直向上建立整车全局坐标系S0。利用车身结构关于XZ平面的对称性，在1/2车身对应的梁单元上取22个主断面为研究对象，其具体位置如图4所示。用上述方法确定的车身主断面编号和名称如表1所示。

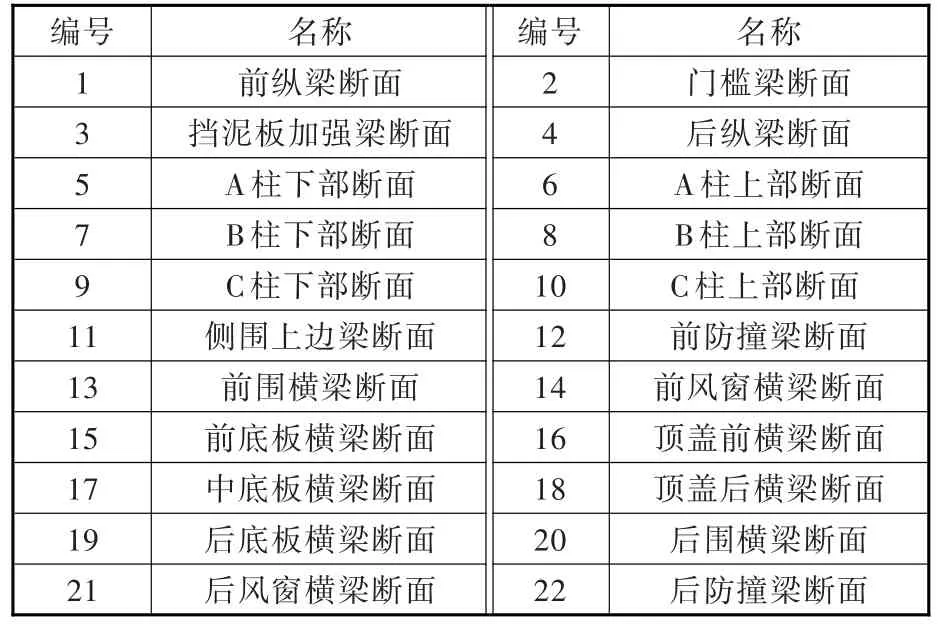
表1 车身主断面编号和名称Tab.1 The numbers and names of main cross-sections of vehicle body

2 基于动态刚度链的车身主断面优化

2.1 模态坐标系下梁单元传递矩阵

车身具有合理的动态特性才能减少振动、控制噪声、提高乘坐舒适性。车身结构的共振，会使乘客感到不舒适，并带来噪声和部件的疲劳损伤，甚至会破坏车身表面的保护层和车身的密封性［10］，因此，在车身概念设计过程中，分析车身的固有振动频率特性，对于合理设计整车的NVH性能具有重要意义。

传递矩阵法［11］涉及矩阵阶次低且能准确建立各节点状态向量与主断面属性之间的关系，适用于刚度链方法的车身正向概念设计。考虑图4中的梁单元i，建立该单元在模态坐标系下的模型（图5），并规定图6所示的应力、载荷、位移的正方向。

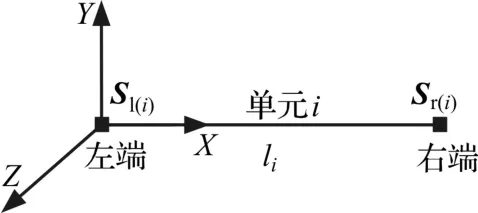
图5 梁单元模型Fig.5 The model of beam element

图6 方向规定Fig.6 Direction regulation

图5中，li为梁单元i长度，可由车身简化几何模型得到，Sl(i)、Sr(i)分别为梁单元i左端和右端节点的状态向量，S=(Fx，Fy，Fz，Mx，My，Mz，x，y，z，Θx，Θy，Θz)T，Fx、Fy、Fz表示沿X、Y、Z轴的力，Mx、My、Mz表示绕X、Y、Z轴的力矩，x、y、z表示沿X、Y、Z轴的线位移，Θx、Θy、Θz表示绕X、Y、Z轴的角位移。

XY平面内横向振动传递方程如下：

XZ面内横向振动传递方程如下：

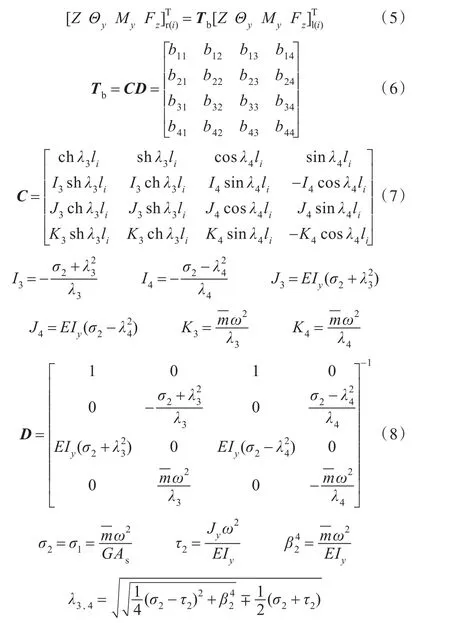
式中，Jy为绕Y轴转动惯量；Iy为横截面对Y轴惯性矩。沿X轴纵向传递方程如下：

式中，EA为抗拉刚度。

绕X轴扭转振动传递方程如下：

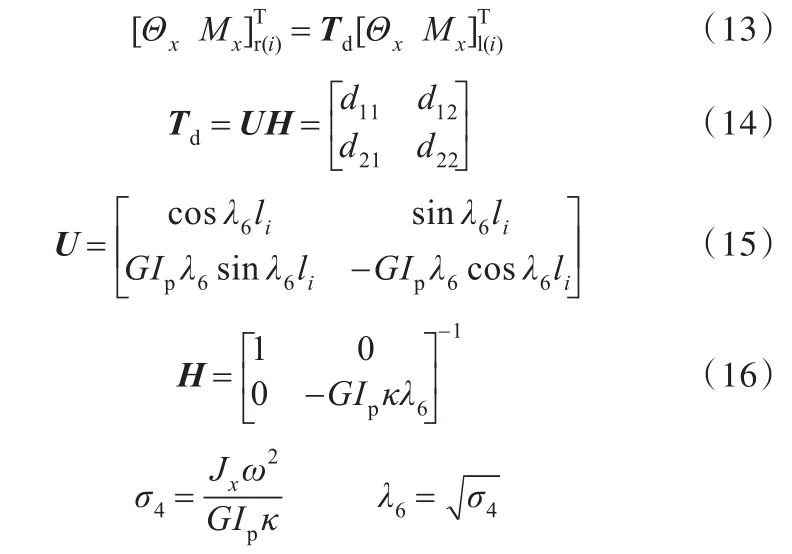
式中，Ip为截面极惯性矩；GIp为抗扭刚度；Jx为绕X轴转动惯量；κ为扭转因子。

由式（1）、式（5）、式（9）、式（13）可整合得到梁单元i左端与右端节点状态向量在横向振动、纵向振动以及扭转振动下的传递矩阵Ti：

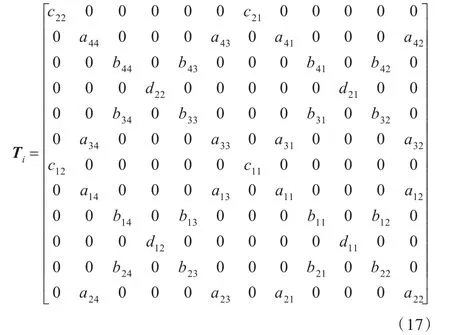
梁单元i两端节点间传递方程为

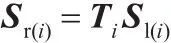
2.2 1/2车身动态刚度链建模

车身结构刚度链以主断面、接头等为节点，以载荷传递路径为链，描述车身几何与拓扑、结构与材料、载荷与变形，以及各子刚度链之间的关系。如白车身整体刚度链由多个子刚度链组合而成，可以分别建立每个子刚度链的计算模型，再向上逐层组合，最终建立车身的完整刚度链模型［12］，如图7所示。

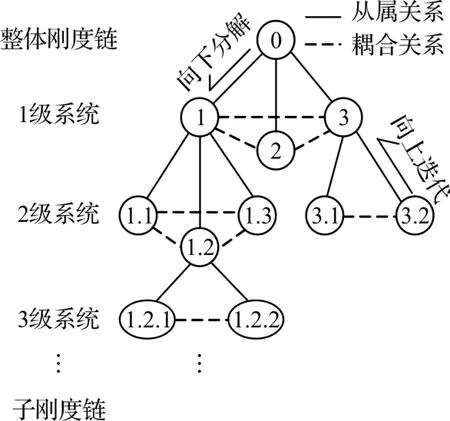
图7 车身刚度链构成关系Fig.7 The constitution relationship for the stiffness chain of vehicle body

白车身动态刚度链建模首先需要分析自重状态下的自由模态，依据图4所示简化几何模型和图7所示构成关系，在无外载荷状态下建立1/2车身动态刚度链模型如图8所示，该系统还可以再分解成若干个子系统。

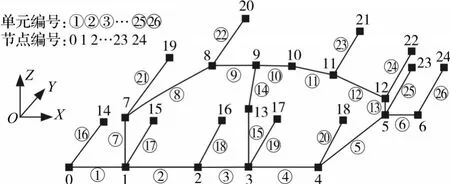
图8 1/2车身动态刚度链模型Fig.8 Dynamic stiffness chain model of 1/2 vehicle body

图8中车身左侧围刚度链由子刚度链0-1-2-3-4-5-6、子刚度链1-7-8-9-10-11-12-5与子刚度链3-13-9组成，整车刚度链由左侧围、右侧围各3条子刚度链及横梁11条子刚度链，共17条子刚度链组成。根据简化几何模型确定的主断面分布将1/2车身梁结构划分成26个单元，25个节点。根据车身设计经验，同一主断面对应多个组成单元时，如门槛梁断面对应单元②、③、④，这些组成单元的截面属性有差别，可将图4中22个主断面细分为图8所示的26个主断面属性集合，主断面名称与表1一致。梁单元i主断面属性记为{C}(i)，i取值为 1，2，…，26，{C}(i)={A，Ix，Iy，Iz}(i)，其中，A为主断面面积（指实心部分面积），Ix、Iy、Iz为主断面惯性矩。

下面基于传递矩阵法，推导车身动态刚度链数学模型，并用车身模态频率来反映动刚度特性。以子刚度链0-1-2-3-4-5-6为例，可以得出由6个梁单元组合成的子刚度链的传递方程如下：

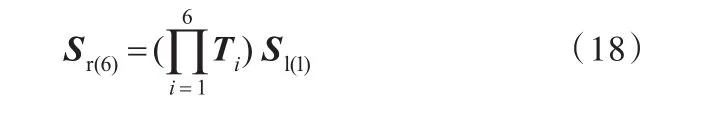
其中，Ti为单元i在全局坐标系下左端与右端节点间的传递矩阵。传递矩阵Ti中的参数，如、GAs、Jx、Jy、Jz等，由材料、梁单元长度及主断面属性确定。其他子刚度链传递方程可同理求得。

当单元的局部坐标系与全局坐标系不平行时（如单元⑤），需进行坐标变换才能求得该单元在全局坐标系下的传递矩阵。

如图9所示，局部坐标系以单元左端为原点，X轴正方向沿单元轴向指向右端。γk、βk、αk为欧拉角，即单元k全局坐标系依次绕Z、Y、X轴旋转直至与局部坐标系三轴方向一致时的旋转角。单元k的传递矩阵从局部坐标系转换到全局坐标系的变换公式为

式中，Tk为单元k在全局坐标系下的传递矩阵；为单元k在局部坐标系下的传递矩阵；Pk为单元k坐标转换矩阵。

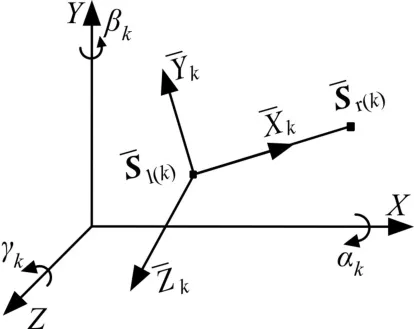
图9 全局坐标系与局部坐标系Fig.9 Global coordinate system and local coordinate system

下面讨论耦合节点处耦合方程的建立。由图8知，单元③、④、○15、○19在节点 3处耦合，其耦合条件为

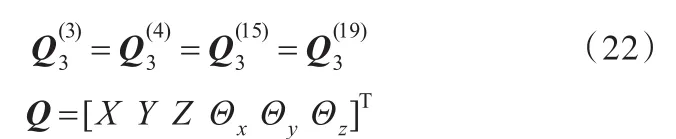
单元n上耦合节点 j处的位移向量记为，同理可得其他耦合节点耦合方程。

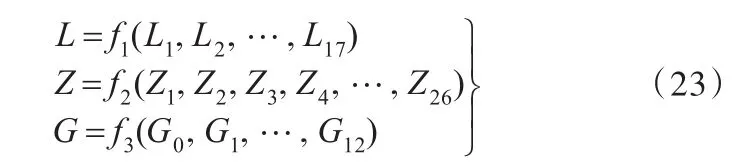
整车刚度链传递方程、坐标转换方程及耦合方程可由各子刚度链传递方程、坐标转换方程及其耦合方程表示，记为 f1、f2、f3。建立整车刚度链数学模型如下：其中，子刚度链i的传递方程记为Li，梁单元 j的坐标转换方程记为Zj，各子刚度链在节点k处的耦合方程记为Gk。车身动态刚度可用车身模态来评价，由式（23）可得车身各主断面属性{C}(i)与车身固有频率 f的关系，记为 f4，即

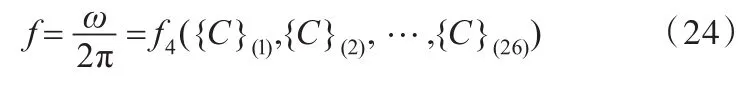
3 主断面优化及结果验证

3.1 车身主断面优化设计

车身整体刚度的优化，取决于各子刚度链抵御变形的贡献，以及各单元材料的优化分配。车身主断面优化设计是一个多学科相互关联和协调的过程［13］。本文综合考虑车身动态和静态性能，以车身轻量化为目标函数，以车身静刚度与固有频率为约束条件，采用遗传算法优化求解主断面的属性参数。

为便于模型求解，将车身主断面形状简化为矩形截面，如图10所示。

图10 主断面简化形状Fig.10 Simplified shape of main cross-sections

26个车身主断面简化矩形截面属性矩阵如下：

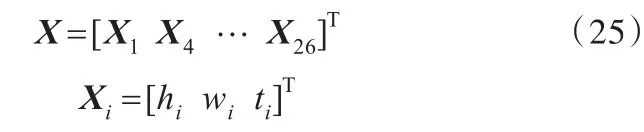
其中，hi、wi、ti分别为梁单元i主断面简化截面结构参数，含义如图10所示。为了减少设计变量，根据车身设计经验，取主断面的长宽比为定值r，r=w/h=1.35，梁单元壁厚t优化区间取［0.6，1.2］mm，门槛梁主断面参数w优化区间取［120，240］mm，其余梁主断面参数w优化区间取［40，200］mm。将车身质量作为目标函数，有

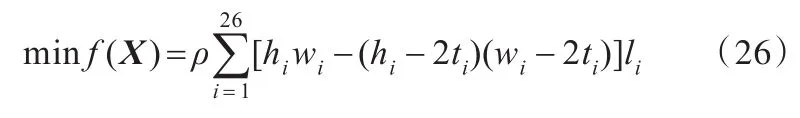
式中，ρ为材料密度。

求解车身静刚度时，载荷加载方式如图11所示，图中约束1、2、3分别指沿坐标轴 X、Y、Z方向的线位移。

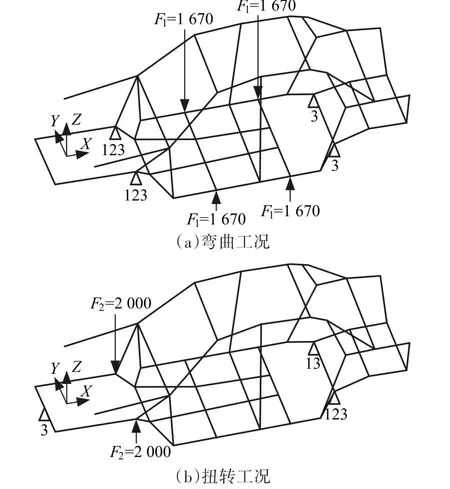
图11 静刚度求解时载荷及边界条件Fig.11 Load and boundary conditions for solving static stiffness

参考同级别车型力学性能，确定相关参数。弯曲刚度要求当施加F1=1 670 N力时，加载点的竖直位移δ小于1 mm；扭转刚度要求当前悬架两铰支点施加F2=2 000 N反向力时，相对扭转角 ϕ不超过0.2 rad，其中，ϕ=arctan(2Δ/b)，b取1 500 mm，为反向载荷加载点间的横向距离，Δ为扭转工况下加载点竖直位移；要求车身一阶固有频率不小于17 Hz。参考文献［14］中车身静态刚度链研究成果可得出δ、ϕ与主断面属性的关系式，分别记为 f5、f6，如下式所示：

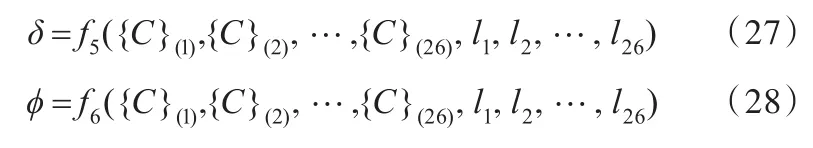
由上述设计变量、目标函数和约束条件组成的优化模型如下：

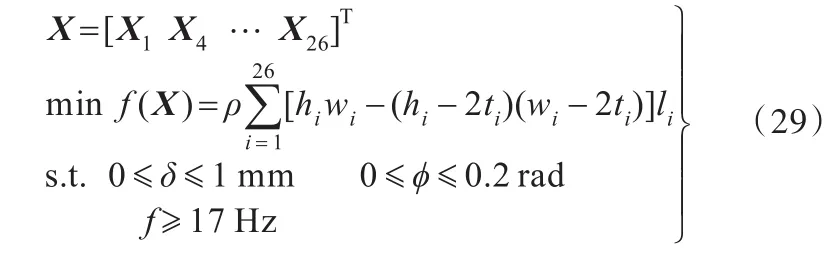
根据上述动态刚度链模型，在MATLAB中编程，采用遗传算法［15-16］求解式（29），目标函数的迭代收敛过程如图12所示。

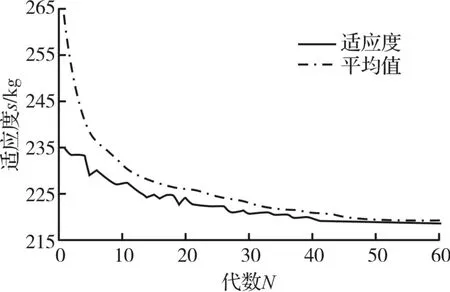
图12 目标函数收敛情况Fig.12 Convergence of objective function

优化后得到的主断面尺寸参数如表2所示。

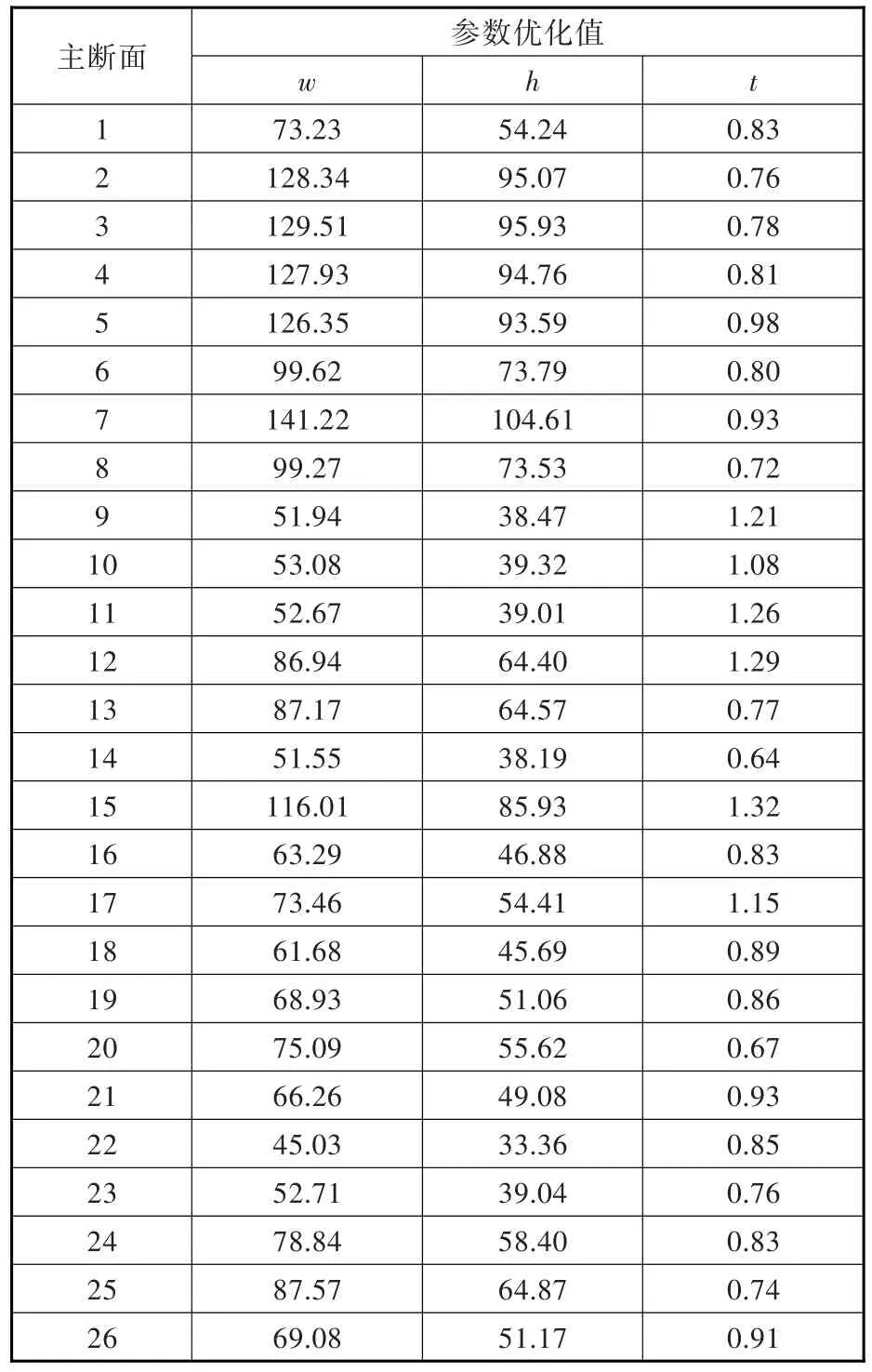
表2 优化后的主断面尺寸参数Tab.2 The size parameters of main cross-sections after optimization mm

利用优化后的主断面尺寸参数，查取对应材料属性可以计算出车身各主断面面积、惯性矩、极惯性矩以及刚度。整车弯曲刚度kW、扭转刚度kN由下式给出：

优化结果下，概念车身在弯曲、扭转工况下的位移及自由模态一阶振型如图13～图15所示。

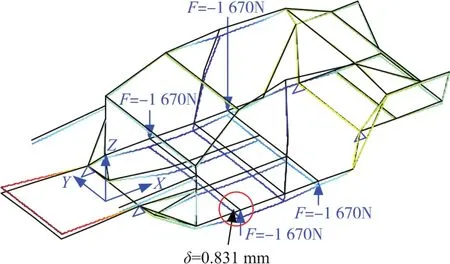
图13 概念车身在弯曲工况下的位移Fig.13 Conceptual car body displacement under bending conditions

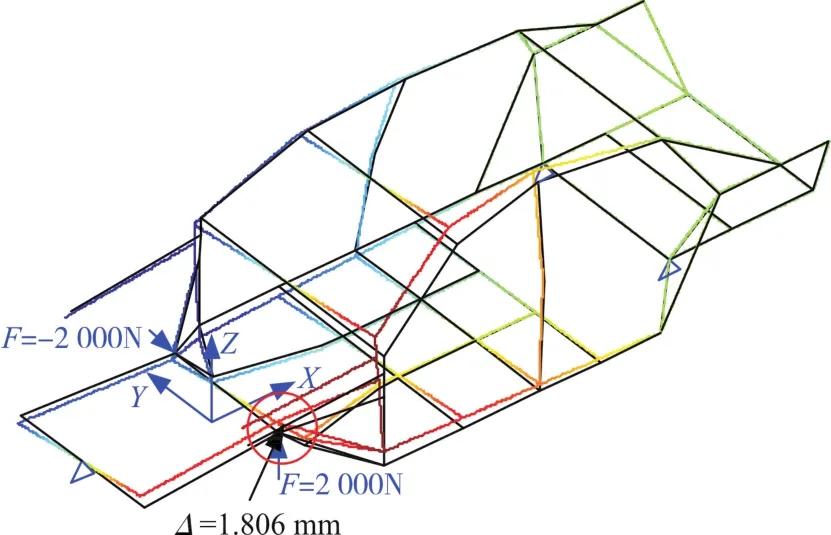
图14 概念车身在扭转工况下的位移Fig.14 Conceptual car body displacement under torsion conditions

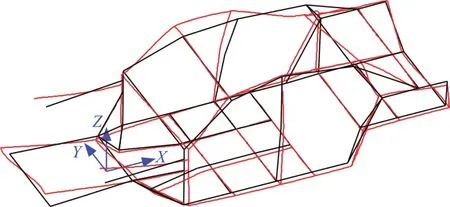
图15 自由模态一阶振型Fig.15 First order modal shape of free mode

优化结果为：在满足静刚度和固有频率约束条件下，车身最轻质量为218.460 2 kg，弯曲工况下加载点的位移为δ=0.831 mm；扭转工况下加载点变形为Δ=1.806 mm，相对扭转角为ϕ=0.138 rad；一阶固有频率为26.8 Hz。

将上述参数值代入式（30）、式（31），得kW=8 038.5 N/mm，kN=21 739.1 N·m/rad。

3.2 优化结果验证

为了验证动态刚度链设计方法的正确性，本文选取一款与设计车型参数近似的标杆车，通过HyperWorks、Nastran对其进行有限元分析，将仿真结果与遗传算法优化结果进行对比分析。在Hypermesh中建立标杆车骨架有限元模型，该模型由196 155个单元、199 093个节点组成，如图16所示。

图16 标杆车有限元模型Fig.16 Finite element model of a benchmarking vehicle

对标杆车骨架有限元模型进行静力以及模态分析，分别得出车身在弯曲、扭转工况及自由模态下的整体变形如图17～图19所示。

图17 标杆车车身弯曲变形Fig.17 Bending deformation of a benchmarking vehicle body

图18 标杆车车身扭转变形Fig.18 Torsion deformation of a benchmarking vehicle body

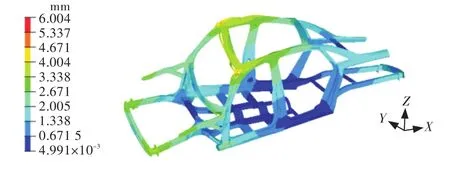
图19 标杆车车身模态分析云图Fig.19 Modal analysis cloud chart of benchmarking vehicle body

标杆车骨架模型弯曲工况下加载点变形量δʹ=1.774 mm；扭转工况下，加载点变形量 Δʹ=1.676 mm，相对扭转角ϕʹ=0.128 rad；一阶模态固有频率为25.2 Hz。

将 上 述 参 数 代 入 式（30）、式（31），得=3 765.5 N/mm ，ʹ=23 437.5 N·m/rad。将动态刚度链求解结果与标杆车分析结果进行对比，结果如表3所示。由于本文建立的刚度链模型没有考虑接头柔度，计算所得弯曲刚度约是标杆车有限元计算结果的两倍，这一结果与文献［17］研究的结论一致。根据表3对比分析结果可知，用动态刚度链方法计算出的扭转刚度及一阶固有频率结果，与标杆车有限元分析得出的结果非常接近，证明了本文研究方法的合理性和可行性。

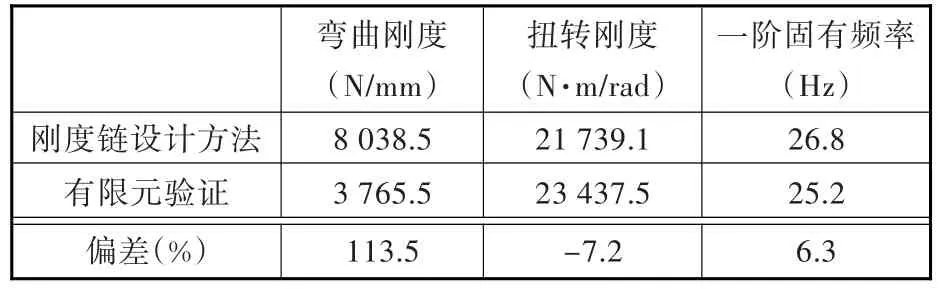
表3 刚度链求解结果与标杆车分析结果对比Tab.3 Comparison between the solution results of stiffness chain and analysis results of benchmarking vehicle

4 结语

本文在综合考虑车身振动特性的基础上提出了车身动态刚度链设计方法，拓展了刚度链方法在车身正向概念设计中的应用范围。将刚度链设计方法所得结果与对应标杆车有限元分析结果进行对比，验证了动态刚度链方法用于车身设计的可行性，为车身正向概念设计提供了参考。

本文的讨论没有考虑接头柔度，采用的也是简化主断面，尽管这样的处理不会对方法的研究产生本质的影响，但建立包含接头柔度和真实主断面形状的动态刚度链模型，仍是将此方法用于车身工程实际需进一步解决的问题。

参考文献：

［1］ ZUO Wenjie.Bi-level Optimization for the Cross-sec⁃tional Shape of a Thin-walled Car Body Frame with Static Stiffness and Dynamic Frequency Stiffness Con⁃straints［J］.Proceedings of the Institution of Mechani⁃cal Engineers Part D Journal of Automobile Engineer⁃ing，2015，229（8）：1046-1059.

［2］ CHEN Wei，ZUO Wenjie.Component Sensitivity Anal⁃ysis of Conceptual Vehicle Body for Lightweight De⁃sign under Static and Dynamic Stiffness Demands［J］.International Journal of Vehicle Design，2014，66（2）：107-123.

［3］ ZIMMER H，PRABHUWAINGANKAR M.Implicitly Parametric Crash and NVH Analysis Models in the Vehicle ConceptDesign Phase［C］//Modeltierung.LS-DYNA Anwender Forum.Hamberg：DYNAmore GmbH，2005：61-69.

［4］ 王磊，刘莹，乔鑫.基于正向开发流程的车身轻量化设计［J］.汽车工程学报，2015，5（6）：461-465.WANG Lei，LIU Ying，QIAO Xin.Lightweight Design of BIW Based on Positive Development Process［J］.Chinese Journal of Automotive Engingeering，2015，5（6）：461-465.

［5］ QIN Huan，LIU Zijian，LIU Yu，et al.An Object-orient⁃ed MATLAB Toolbox for Automotive Body Conceptual Design Using Distributed Parallel Optimization［J］.Ad⁃vances in Engineering Software，2017，106（4）：19-32.

［6］ 刘子建，饶俊威，刘瑜，等.基于主断面参数的车身结构刚度链快速求解［J］.湖南大学学报（自然科学版），2017，44（2）：1-8.

LIU Zijian，RAO Junwei，LIU Yu，et al.Fast Calcula⁃tion for the Stiffness Chain Model of Car body Based on Parameters of Main Section［J］.Journal of Hunan University（Natural Science），2017，44（2）：1-8.

［7］ 陈毅强，刘子建.电动汽车车身的回传射线矩阵刚度链分析方法［J］.中国机械工程，2016，27（23）：3252-3258.

CHEN Yiqiang，LIU Zijian.Reverberation-ray Matrix Stiffness Chain Analysis Method for Electric Vehicle Body［J］.China Mechanical Engineering，2016，27（23）：3252-3258.

［8］ 刘保公.碳纤维复合材料纯电动汽车车身结构优化设计［D］.长沙：湖南大学，2016.LIU Baogong.The Optimization Design of Carbon Fi⁃ber Reinforced Plastic of Pure Electric Vehicle Body Structure［D］.Changsha：Hunan University，2016.

［9］ 张志亮.逆向工程开发技术及其在福田重卡车身开发中应用［D］.大连：大连理工大学，2003.

ZHANG Zhiliang.Reverse Engineering Development Technology and Its Application in Foton Heavy Truck Body Development［D］.Dalian：Dalian University of Technology，2003

［10］ 张哲蔚.基于简化模型的车身结构分析与优化［D］.上海：同济大学，2009.

ZHANG Zhewei.Analysis and Optimization of Car Body Structure Based on Simplified Model［D］.Shanghai：Tongji University，2009.

［11］ 芮筱亭.多体系统传递矩阵法及其应用［M］.北京：科学出版社，2008.

RUI Xiaoting.Transfer Matrix Method of Multibody System and Its Application［M］.Beijing：Science Press，2008.

［12］ 田海豹.基于刚度链方法的车身概念设计研究［D］.长沙：湖南大学，2013.

TIAN Haibao.Study on Conceptual Design of Car Body Using Stiffness Chain［D］.Changsha：Hunan University，2013.

［13］ KODIYALAM S，YANG R J，GU L，et al.Multidisci⁃plinary Design Optimization of a Vehicle System in a Scalable，High Performance Computing Environment［J］.Structural& Multidisciplinary Optimization，2004，26（3）：256-263.

［14］ 刘子建，周小龙，田海豹，等.基于主断面刚度优化分配的车身正向概念设计［J］.中国机械工程，2015，26（6）：837-843.LIU Zijian，ZHOU Xiaolong，TIAN Haibao，et al.For⁃ward Concept Design of Car Body Using Stiffness Op⁃timal Allocation of Main Sections［J］.China Mechani⁃cal Engineering，2015，26（6）：837-843.

［15］ GAAFAR L K，MASOUD S A.Genetic Algorithms and Simulated Annealing for Scheduling in Agile Manufacturing［J］.International Journal of Produc⁃tion Research，2005，43（14）：3069-3085.

［16］ 陈伦军.机械优化设计遗传算法［M］.北京：机械工业出版社，2006.CHEN Lunjun.Genetic Algorithm for Mechanical Op⁃timalDesign［M］.Beijing： Machinery Industry Press，2006.

［17］ MALEN D E.Fundamentals of Automobile Body Structure Design［M］.Pennsylvania：SAE Internation⁃al，2011.

（编辑 王艳丽）

作者简介：胡裕菲，男，1993年生，硕士研究生。研究方向为车身结构优化与车身NVH。E-mail：huyufei@hnu.edu.cn。刘子建（通信作者），男，1953年生，教授、博士研究生导师。研究方向为车身刚度链理论、机械精度链理论、产品信息模型理论。发表论文100余篇。E-mail：zijianliu@hnu.edu.cn。