刀具工件双旋转运动机床加工过程的能量效率获取方法

张西成 刘 飞 刘培基

重庆大学机械传动国家重点实验室，重庆，400044

0 引言

制造系统能耗总量巨大且能量效率普遍很低，提升制造系统能量效率已成为各国制造业可持续发展的关键战略［1］。如欧盟发布了《2030气候和能源框架》，计划到2030年将能量效率至少提升27%［2］；美国能源部宣布向清洁能源制造创新研究所投资7000万美元用于制造过程能量效率和生产率的提升研究，计划至少提升能量效率15%和生产率50%［3］。由此可见，制造系统能量效率的研究意义重大，已成为各国制造业可持续发展的一个重大战略课题。

机床是制造系统的制造主体和能耗主体，同样具有能量消耗总量巨大、能量效率普遍很低以及节能潜力很大等特点。现有关于机床能效的研究主要集中在机床能效预测、监控与管理等方面，如VIJAYARAGHAVAN等［4］建立了机床能量效率自动监控框架，ALTINTAŞ等［5］为了提高加工过程能量效率，提出了一种铣削过程的能耗预测模型，LEE［6］等建立了一种可适应于各种机床的能耗模型，ABELE等［7］通过分析机床主轴单元的能耗来确定机床的能量效率提升潜力，日本标准协会基于参考零件法发布了机床能量效率评价系列标准［8］，国际标准化委员会起草了机床的环境评估标准（ISO 14955）［9］，LENZ等［10］通过高频采集 PLC信号来定量分析能耗组件的节能潜力，刘高君等［11］研发了一体化的机床多源能耗状态信息在线检测系统。然而，将现有的研究成果应用在实际中仍存在挑战性，为了实现机床的能量效率预测、监控与管理，需要建立长期有效的机床能量效率获取方法。

对于机床能量效率获取方法，现有研究已取得大量成果。GUTOWSKI等［12］和KARA等［13］均提出了以去除单位体积或单位质量工件材料所耗能量的比能模型来衡量机床的能量效率，该模型虽然便于比较两台不同机床的能量效率，但难以反映机床的实时能量效率状态；LIU等［14］提出了一种切削功率与机床总输入功率之比的能量效率瞬态模型，但该模型中的实时切削功率极难获取。现有的切削功率获取方法中，直接法是通过安装传感器、测力仪、功率仪等来直接获取切削力、切削力矩或切削功率，但该方法难以应用于切削力测量仪器安装特别困难的机床，如滚齿机、剃齿机、磨齿机等刀具工件双旋转运动机床；经验模型法和理论模型法存在模型适用范围窄、参数获取困难，难以反映加工过程切削力的瞬态变化等问题。HU等［15］通过分析机床主传动系统载荷损耗能量与切削功率、传动系统组成部件基础参数间的关系，建立了数控机床能量效率在线获取方法；但是，为了获取机床载荷损耗系数，该方法需要安装切削仪器和开展多组切削实验，依旧难以应用于切削力测量仪器安装特别困难的机床。VELCHEV等［16］基于经验公式建立了工艺参数与机床能耗关联模型，但该模型不具有普遍适用性。刘培基等［17］根据数控机床主传动系载荷能量损耗模型提出了一种载荷损耗系数计算获取方法，并在车床上进行了准确性验证，但刀具工件双旋转运动机床的有效能量主要由刀具轴有效能量和工件轴有效能量两部分组成，因此，该方法也无法应用到刀具工件双旋转运动机床上。

针对上述情况，本文提出了一种关于刀具工件双旋转运动机床的加工过程能量效率获取方法。

1 刀具工件双旋转运动机床能量效率模型

1.1 有效能量组成

刀具工件双旋转运动机床和其他机床一样，具有机械加工过程的时段特性，从机床上电到加工结束共包括7个时段，即机床电气启动时段、机床待机时段、主电机启动时段、主电机空载时段、快速进给时段、空走刀时段、切削加工时段。机械加工过程能耗模型为

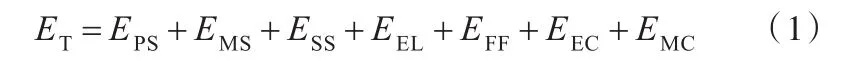
式中，ET为机械加工过程消耗的总能量；EPS为机床电气启动时段消耗的能量总和；EMS为机床待机时段消耗的能量总和；ESS为主电机启动时段消耗的能量总和；EEL为主电机空载时段消耗的能量总和；EFF为快速进给时段消耗的能量总和；EEC为空走刀时段消耗的能量总和；EMC为切削加工时段消耗的能量总和。

机械加工过程的切削加工时段有效能量研究是机床能量效率研究的关键，图1为刀具工件双旋转运动机床动力系统在切削加工时段的功率平衡框图。

图1 机床动力系统功率平衡框图Fig.1 The power balance diagram of machine dynamical system

由图1可以看出，机床在切削加工过程中的有效功率为机床动力系统的输出功率，即为机床所有进给系统和传动系统的输出功率之和，表达式如下：

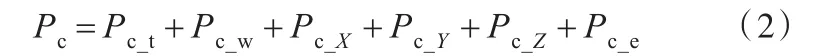
王秋莲等［18］指出机床有效能量的定义有狭义和广义之分：广义上，有效能量可以指所有能量流的有效输出之和；狭义上，有效能量仅指机床的切削能量。现有的关于机床能量效率获取研究中，有效能量的获取主要通过主轴输入功率分离得到，并没有考虑其他轴的输出功率。对于绝大多数机床来说，仅考虑主轴的有效能量，对能量效率的影响并不大；但对于刀具工件双旋转运动机床来说，其工件轴属于连续进给，进给速度不可忽略，因此，工件轴提供的有效能量不可忽略，而其他进给轴的输出功率与刀具轴和工件轴的输出功率相比，可以不计。本文在研究刀具工件双旋转运动机床的能量效率时，将刀具轴和工件轴的输出功率之和作为机床的有效功率，即

1.2 能量效率模型

现有的关于机床能量效率的定义主要分为三种，即瞬态能量效率、过程能量效率和比能效率，具体如表1所示。其中，tc为机床总加工时间；ttotal为机床总运行时间。

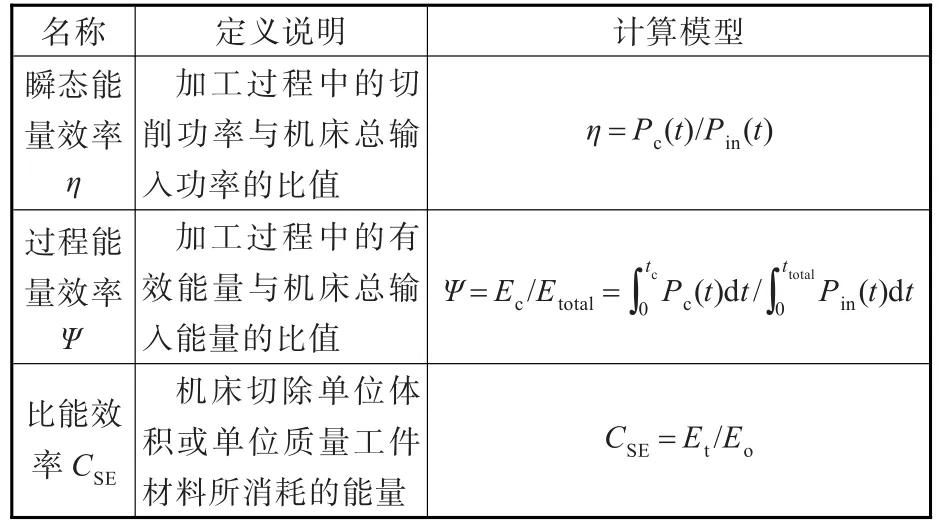
表1 能量效率定义相关信息Tab.1 The definition of energy efficiency

由于刀具工件双旋转运动机床加工过程的切削功率和机床总输入功率均是瞬态值，导致能量效率η值为瞬态变化量，无法用于定量分析刀具工件双旋转运动机床加工过程能量效率。比能效率和过程能量效率便于企业进行能效管理（如能耗限额［19］），但不能很好地反映机床的实时能效状况。过程能量效率是瞬态能量效率的积分形式，前者可定量分析机床的能量效率，后者可实时反映机床的能效状况，因此，本文分别依据瞬态能量效率和过程能量效率的定义来计算刀具工件双旋转运动机床的能量效率。结合刀具工件双旋转运动机床的有效能量组成，可得刀具工件双旋转运动机床的过程能量效率新模型，即式中，Pc_ti为机床加工时段i刀具轴的有效功率；Pc_wi为机床加工时段i工件轴的有效功率；Qc为机床加工时段总数；Qm为机床运行时段总数；Eci为机床加工时段i的有效加工能量；twork_i为机床在运行时段i的运行总时间；tcut_i为机床在加工时段i的加工总时间。

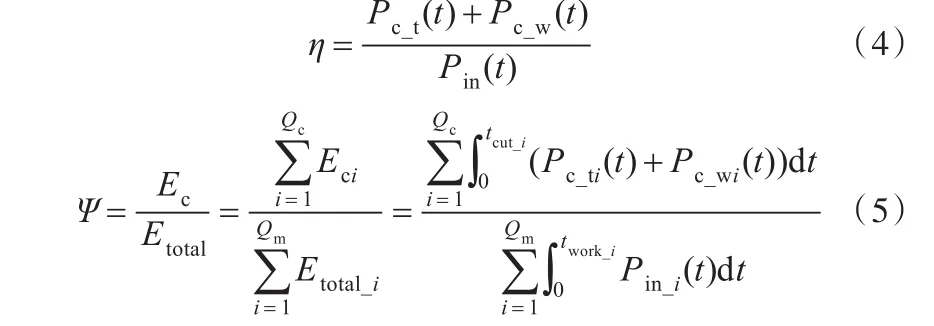
2 刀具工件双旋转运动机床能量效率获取方法

从式（4）、式（5）可以看出，获取工件轴和刀具轴的有效功率是刀具工件双旋转运动机床能量效率获取的关键。为此，本文通过分析刀具轴和工件轴的能耗组件，建立载荷损耗系数计算模型，从而根据载荷损耗系数计算获取有效功率。

2.1 刀具轴载荷损耗系数计算模型

刀具工件双旋转运动机床的刀具轴能耗组件主要包括变频器、伺服电机和机械传动部分，由此可得刀具轴加工过程的能量流平衡方程：

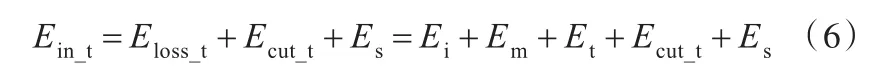
根据刀具轴能耗用途分，可得刀具轴加工过程的功率平衡方程：

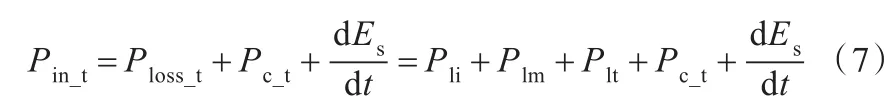
式中，Ein_t为输入刀具轴的总能量；Pin_t为输入刀具轴的总功率；Eloss_t为传动系统损耗能量，由变频器损耗Ei、电机损耗 Em、机械传动损耗Et三部分组成；Ploss_t为能耗组件总损耗功率，由变频器损耗功率Pli、电机损耗功率Plm、机械传动损耗功率Plt三部分组成；Ecut_t为用于切削加工的能量（切削能量）；Es为传动系统的广义储能；为传动系统广义储能的变化率。

对于某一加工时刻，刀具轴传动系统的瞬态能量流方程为

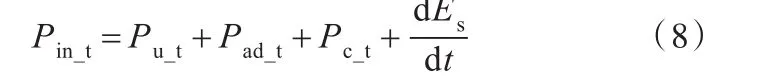
式中，Pu_t为刀具轴空载功率；Pad_t为刀具轴载荷损耗功率。

结合式（7）和式（8），可得

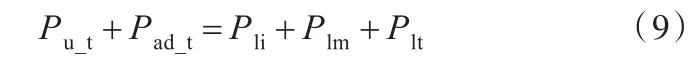
文献［20］指出，机床主传动系统的载荷损耗功率Pad与切削功率近似成二次函数关系，即

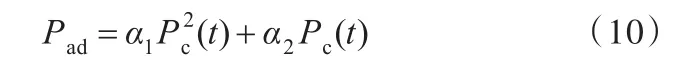
式中，α1、α2为传动系统载荷损耗系数。

结合式（9）、式（10），可得

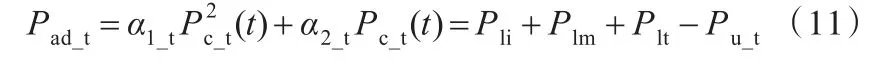
文献［17］对数控机床主传动系统的变频器功率损耗、电动机功率损耗进行了深入研究并提出了相应的功率损耗模型。变频器功率损耗模型为

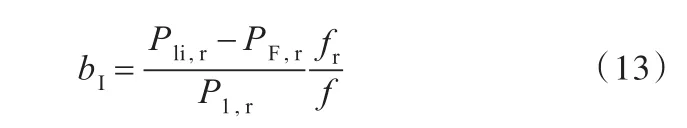
式中，P1为变频器输出功率；PF，r为散热器功率损耗；P1，r为变频器额定输出功率；Pli，r为额定电流下变频器的功率损耗；f为变频器输出电流中基波电流的频率；fr为电动机的基频。

电动机的功率损耗模型为

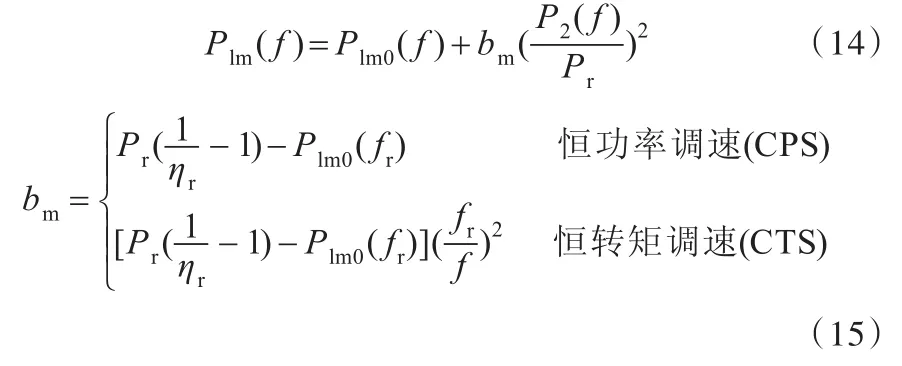
式中，Plm0为电动机基频下的空载损耗；P2为电动机输出功率；Pr为电动机额定功率；ηr为电动机额定状态时的效率。

文献［21］对机床机械传动系统各传动环节的能量传输及能量损耗状况进行分析，建立了机床机械传动系统的能量传输数学模型：

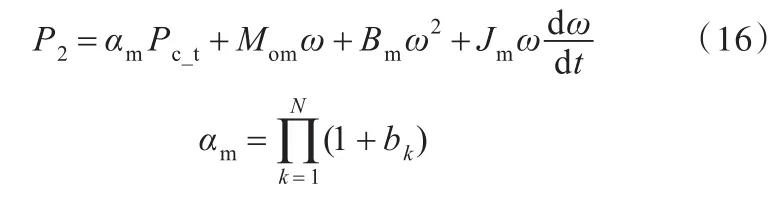
式中，αm为机械传动系统的载荷系数；bk为第k传动环节载荷系数；ω为电动机角速度；Bm为机械传动系统等效到电机轴上的黏性阻尼系数；Jm为机械传动系统等效到电机轴上的转动惯量；Mom为机械传动系统等效到电机轴上的非载荷库仑摩擦力矩。

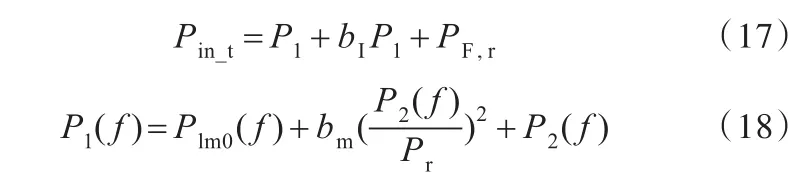
则结合式（17）、式（18）可得

又由于Pin_t、P1、P2之间存在如下的关系：

式中，P2u为刀具轴机械传动部分的空载损耗功率。

整个刀具轴的空载功率

结合式（8）、式（16）、式（19）、式（20）可得

结合式（10）、式（21）便可得载荷损耗系数的表达式：

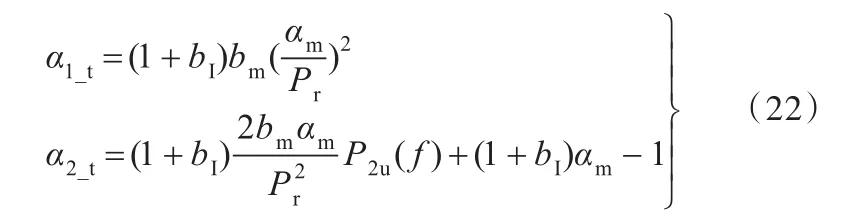
又由于刀具轴电机输入功率和输出功率满足如下关系式：

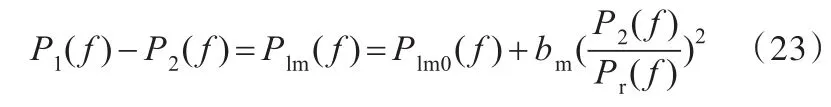
因此，可得刀具轴电机输出功率的表达式：

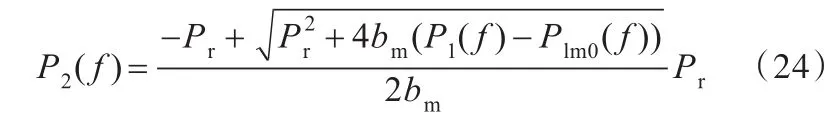
结合式（17）、式（20）、式（24）可得刀具轴机械传动部分的空载损耗功率表达式：

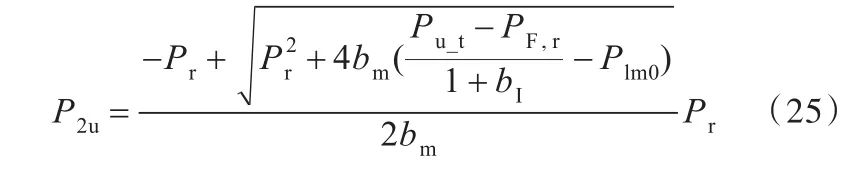
从式（22）、式（25）可以看出，通过查询变频器手册、电动机手册以及机床手册便可以计算得到机床刀具轴的载荷损耗系数α1_t、α2_t。

2.2 工件轴载荷损耗系数计算模型

对于刀具工件双旋转运动机床来说，工件轴相当于机床的一组进给系统，其能耗组件主要由交流伺服驱动器、伺服电机和机械传动部分组成。

根据文献［22］可知，交流伺服驱动器在运行状态下的总功耗由3个绝缘栅极双极型晶体管（IGBT）功耗和3个续流二极管功耗组成，即

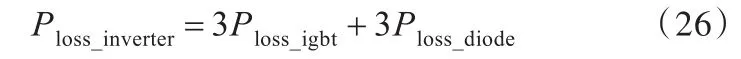
其中，IGBT功耗主要由IGBT通态损耗和IGBT开关损耗组成［23］，文献［24］给出了 IGBT通态损耗PSS和IGBT开关损耗PSW的数学模型：

式中，M 为幅值调制比；cosφ为负载功率因素；ICP为正弦波电流峰值；UCE0为IGBT通态压降；RCE为IGBT通态等效电阻；fSW为IGBT开关频率；Udc为直流母线电压；ESW(on)P为额定电流、电压下IGBT开通一次损耗的能量；ESW(off)P为额定电流、电压下IGBT关闭一次损耗的能量；ICN为额定工作电流；UCEN为额定工作电压。

同样，续流二极管的损耗也由二极管通态损耗PDC和二极管开关损耗 Prr组成。其中，通态功耗模型如下［24］：

式中，UF0为二极管门槛电压；RF为二极管通态等效电阻。

文献［25］指出，二极管开关损耗计算过程中主要关注二极管关断过程中引起的反向恢复损耗，开通损耗可忽略不计，其功耗模型如下：

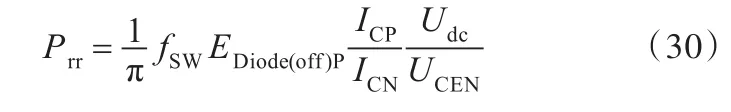
式中，EDiode(off)P为额定电流、电压下二极管关断一次的损耗。

综上所述，交流伺服驱动器的功耗模型为

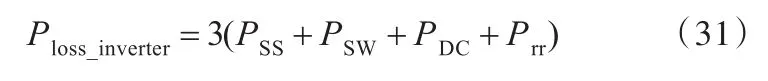
结合式（27）～式（31）便可得伺服驱动器的功率损耗是关于正弦波电流峰值ICP的二次函数，即

式中，a、b为常数，分别为二次函数二次项系数和一次项系数；PWM表示脉冲宽度。

文献［26］通过分析研究数控机床传动系统的能耗组件，建立了“伺服电机+机械传动系统”的功率模型：

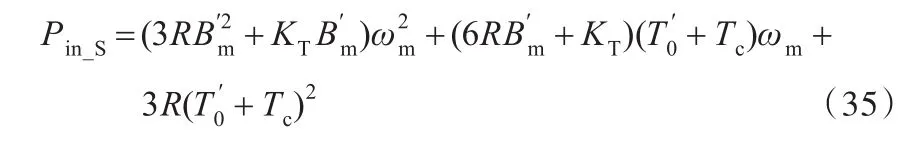
式中，Pin_S为输入伺服电机的功率；Rʹ为伺服电机定子绕组电阻；为等效阻尼系数；KT为转矩系数；ωm为电机轴转速；为电机内部损耗转矩与转矩系数的比值；Tc为切削矩。

结合式（32）、式（35）可得输入工件轴功率模型：

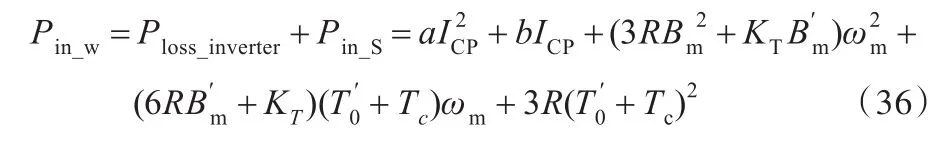
当切削矩Tc等于零时，可得工件轴的空载功率：

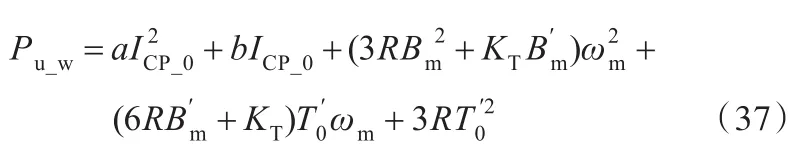
式中，ICP_0为空载时驱动器正弦波电流峰值。

因此，结合式（36）、式（37）可得工件轴的载荷损耗功率模型：

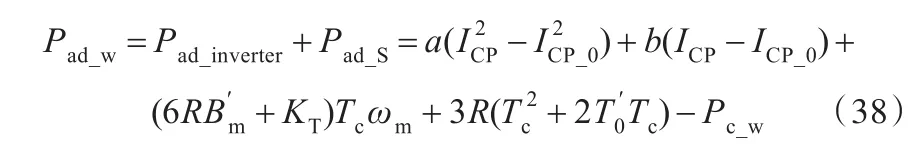
式中，Pad_inverter为驱动器附加载荷损耗；Pad_S为电机加机械部分载荷损耗。

由于式（38）中的系数a、b参数众多，难以获取，本文根据现有关于机床载荷损耗研究中一次载荷损耗系数的取值范围近似认为Pad_inverter=0.2Pactive_S，Pactive_S为驱动系统的有效能量；同时，为电机和机械传动部分的空载功率。由此可得

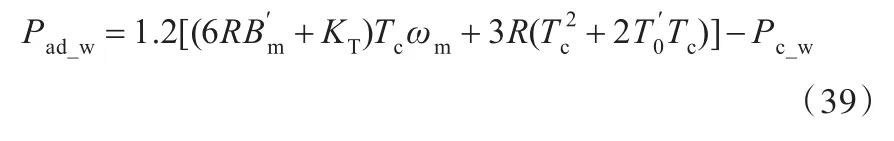
另外，结合切削矩的计算公式：Tc=9 550Pc_w/(1 000n)（n为工件轴转速，r/min；Pc_w为工件轴输出功率，W），计算可得

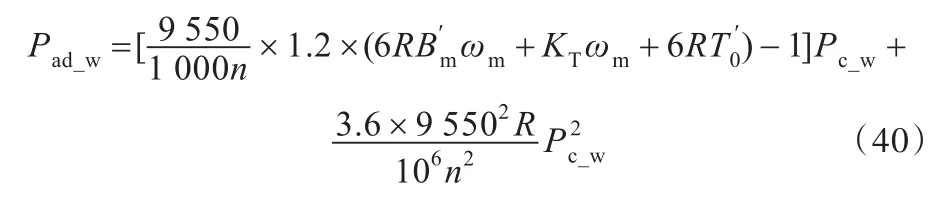
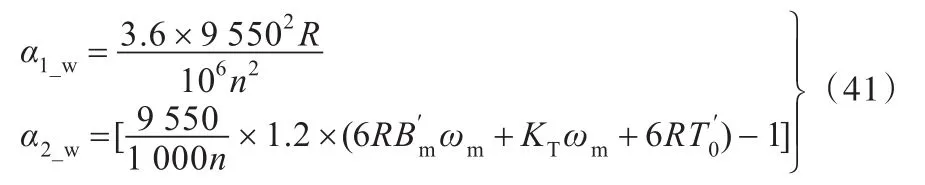
因此，可得工件轴载荷损耗系数的表达式：损耗系数 bk，代入计算机械传动系统的载荷系数αm。

在机床刀具轴输入端安装功率传感器，测量得到刀具轴空载运动时的输入功率Pu_t，代入式（25）计算 P2u。

最后，将 bI、bm、αm、P2u、Pr代入式（22）计算得到刀具工件双旋转运动机床的刀具轴载荷损耗系数 α1_t、α2_t。

2.3 载荷损耗系数计算获取方法

2.3.1 刀具轴载荷损耗系数的计算

查询变频器手册，获取散热器功率损耗PF，r、变频器额定输出功率 P1，r、额定电流下变频器的功率损耗Pli，r、变频器输出电流中基波电流的频率 f和电动机的基频 fr，代入式（13）计算bI。

查询刀具轴电机手册，获取电机基频下的空载功率损耗Plm0、电机额定功率Pr以及电动机额定状态时的效率ηr，代入式（15）计算bm。

查询机床手册，获取机床刀具轴机械传动系统传动环节的数量N以及第k传动环节的载荷

2.3.2 工件轴载荷损耗系数的计算

查询工件轴伺服电机参数，获取伺服电机的转矩系数KT以及伺服电机定子绕组电阻R。根据机床加工工艺卡片，获取工件轴伺服电机的转速n以及角速度ωm。

由式（41）可以看出，要计算得到工件轴的载

荷损耗系数，还需要获取得到等效阻尼系数和电机内部损耗转矩与转矩系数的比值；文献［26］给出了伺服电机的电流 Is与转速之间的关系式：

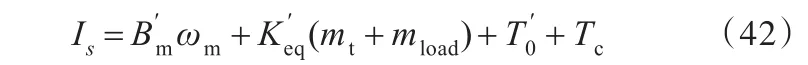
式中，Kʹeq为关于电机节距 p的函数；mt为工作台质量；

mload为工作台上的负载质量。

对于一般数控机床，可推算得出的取值数量级为可以忽略不计，因此：

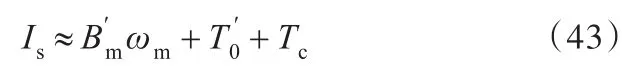
电机空载电流Isu与转速ωm满足如下关系：

将式（44）改成矩阵形式：

因此，通过多组实验，测取多组电机空载电流与转速，用最小二乘法可辨识出

将代入式（41）计算，即可得到刀具工件双旋转运动机床工件轴的载荷损耗系数α1_w、α2_w。

2.4 能量效率计算获取方法

当刀具工件双旋转运动机床处于稳态运行状态时，无论是刀具轴还是工件轴均满足如下的功率平衡方程：

由式（10）可得

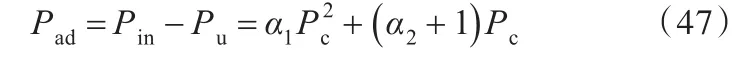
由于有效功率 Pc≥0，因此，解方程得

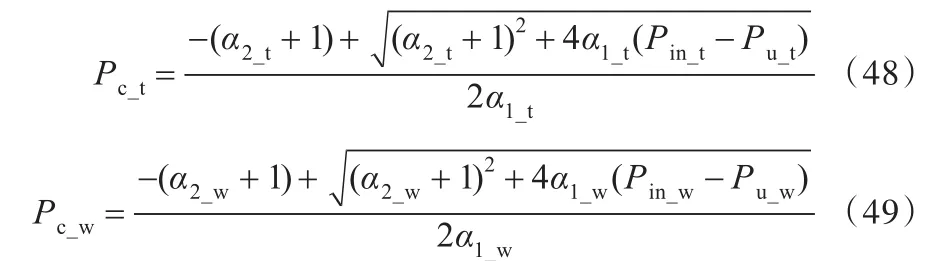
在获得刀具轴和工件轴的载荷损耗系数后，只需测取刀具轴、工件轴的输入功率和空载功率，便可计算刀具轴和工件轴的输出功率。其中，输入功率和空载功率的获取可通过安装功率传感器测取，而无需安装切削仪器。

分别获取得到刀具轴和工件轴的有效功率Pc_t、Pc_w后，刀具工件双旋转运动机床的有效能量

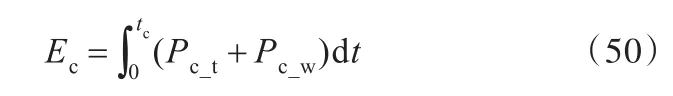
通过在机床总电源处安装功率传感器，测取机床的总输入功率PM_in，则刀具工件双旋转运动机床的总输入能量

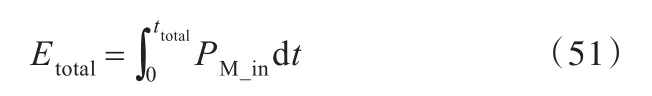
结合式（4）、式（48）、式（49）可计算得刀具工件双旋转运动机床的瞬态能量效率η；结合式（5）、式（50）、式（51）可计算得刀具工件双旋转运动机床的过程能量效率Ψ。

3 实验验证

为验证本文提出的刀具工件双旋转运动机床能量效率计算获取方法的准确性，需要在刀具工件双旋转运动机床上安装切削力测量仪；但是，实验研究发现在刀具工件双旋转运动机床（如滚齿机、剃齿机、磨齿机等）上安装切削力测量仪器（如瑞士Kistler9257B多功能三分力测力仪）特别困难，而且极易影响机床的刚度，导致加工过程中振动剧烈。由此，有必要设计实验来间接验证本文所提出方法的精度。

本文刀具轴和工件轴的有效功率获取方法，是通过建立刀具轴和工件轴载荷损耗系数理论模型而提出的。由于上述载荷损耗系数理论模型是通用模型，可用于计算获取所有由驱动器（变频器或伺服驱动器）、伺服电机和机械传动部分组成的传动系统载荷损耗系数，因此，本文可通过在另外一台与刀具工件双旋转运动机床具有类似传动系统结构的机床上进行间接验证。选择PL700型数控加工中心作为研究对象，该加工中心与刀具工件双旋转运动机床同样具有由驱动器（变频器或伺服驱动器）、伺服电机和机械传动部分组成的传动系统。

获取PL700型数控加工中心的相关基础参数，如表2所示。

表2 数控加工中心PL700的基础参数Tab.2 Basic parameters of machining center PL700

为了验证上述计算方法的准确性，本文采用控制变量法，在15组不同加工参数下进行切削加工实验，对每一组结果进行误差分析，加工参数如表3所示。

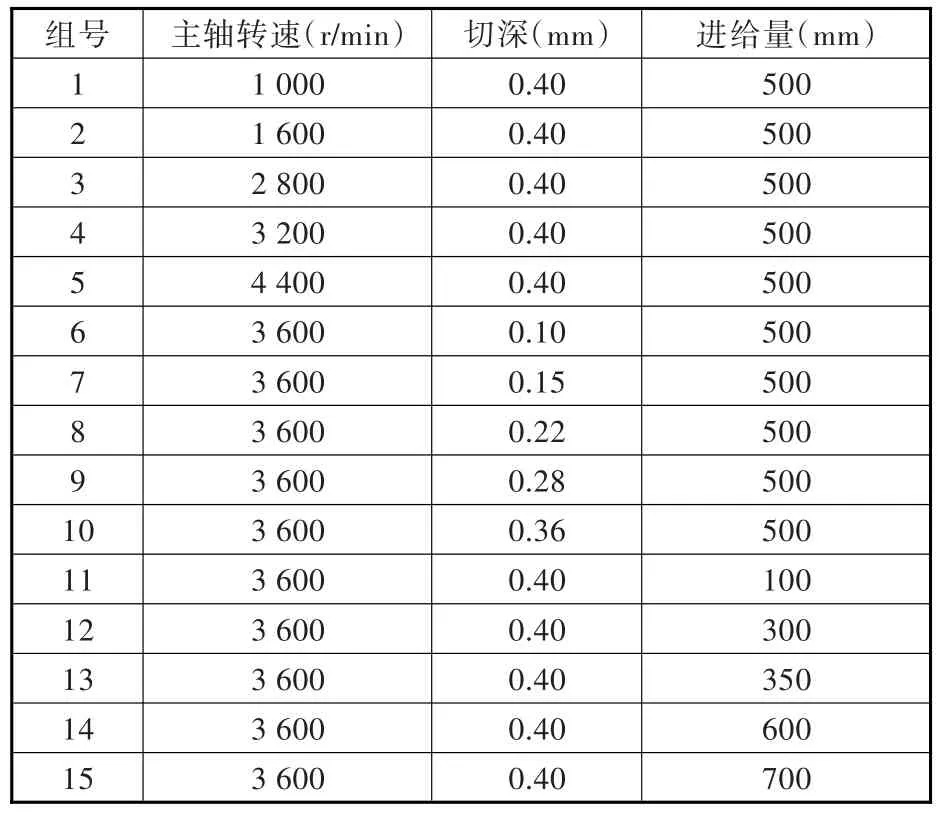
表3 加工实验选用的15组加工参数Tab.3 Cutting parameters in verifying experiments

加工实验开始前，在主轴处安装了HIKIO-3390C功率测量仪，用于测量主轴的空载功率和主轴总输入功率；在切削区域安装了瑞士Kistler9257B多功能三分力测力仪，用于测量加工过程中的切削力大小。最终实验测量所得功率值与计算所得功率值的对比如图2a所示，相对误差结果如图2b所示。

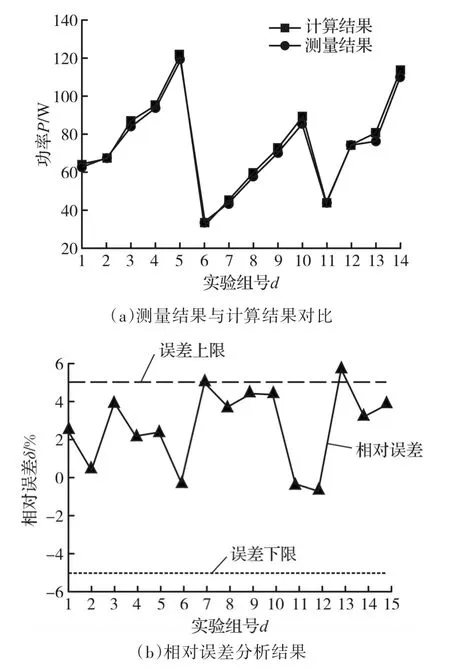
图2 结果与误差分析Fig.2 Results and relative error analysis

由图2a可以看出，整个实验数据的计算结果与用公认标准测试仪器所测量的结果比较接近，具有较高的精度，同时，也存在一定的误差。由图2b可以看出，相对误差值基本都在±5%以内，只有极个别数值落在了5%误差线以外，主要原因是由于在实际加工中如电压波动、工件表面不平整等各种随机误差导致具体加工过程中的测算精度下降。由此，可以说明本文所提出方法具有一定的准确性，可以用于机床能量效率的计算。

4 应用案例研究

将本文提出的能量效率获取方法在重庆机床（集团）有限责任公司YS3126CNC7型数控滚齿机上进行了应用。查看该型号机床的刀具轴和工件轴组成部件的说明书、电机铭牌等，获得相关基础数据，如表4所示。

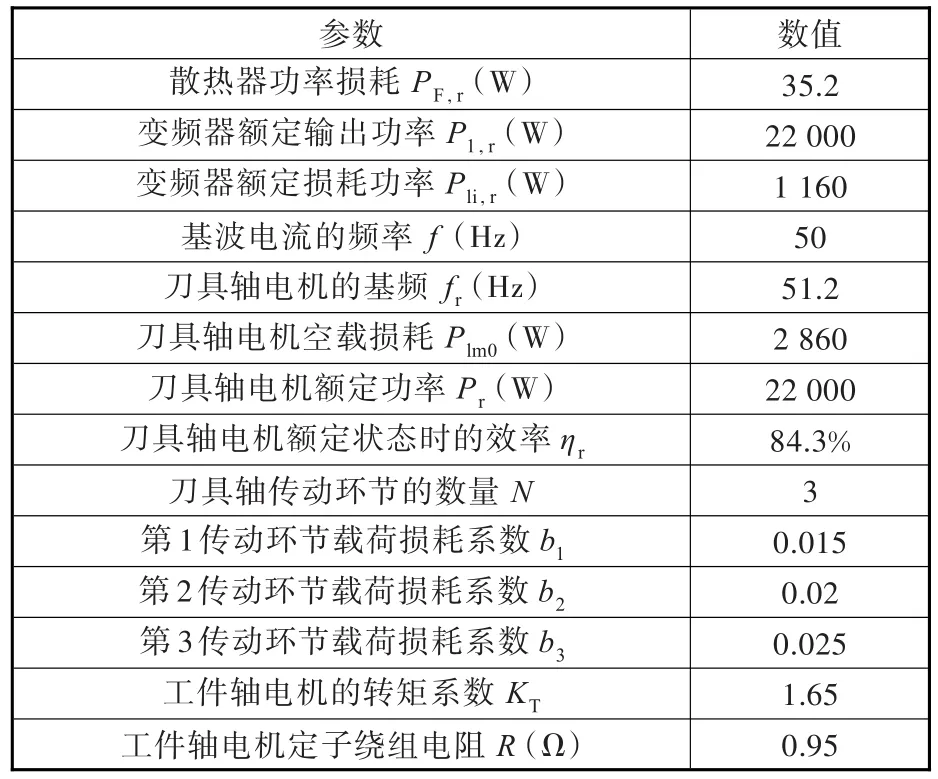
表4 YS3126CNC7型数控滚齿机的基础数据Tab.4 Basic data of gear hobbing machine YS3126CNC7

在YS3126CNC7型数控滚齿机上进行工件轴等效阻尼系数和电机内部损耗转矩与转矩系数的比值辨识实验。选取30组不同工件轴转速进行实验，得出工件轴电机空载电流与电机角速的曲线，如图3所示，通过最小二乘法辨识出工件轴参数方程为：Isu=0.167ωm+0.798，即辨识出分别为0.167和0.798。

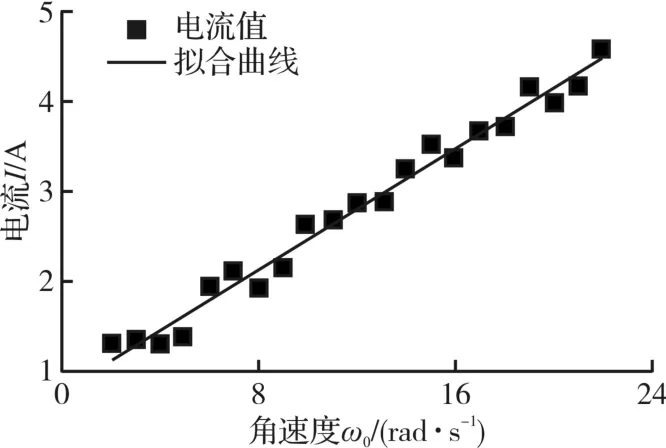
图3 空载运行时电流-角速度拟合曲线Fig.3 Tare-current curve in term of angular velocity

在YS3126CNC7型数控滚齿机上进行滚齿加工实验，其加工参数如表5所示。

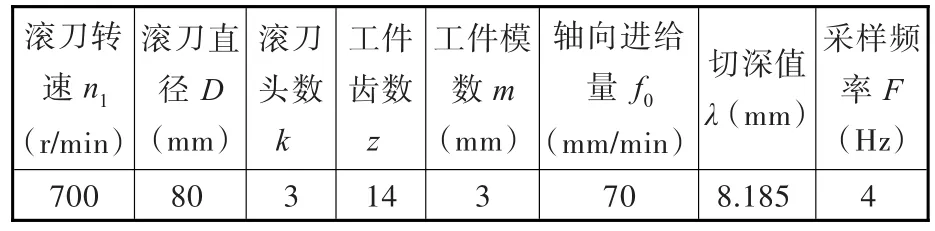
表5 加工参数Tab.5 Processing parameters

应用HIOKI-3390C功率仪测取不同转速下刀具轴的输入功率，即Pu_t，如图4所示。

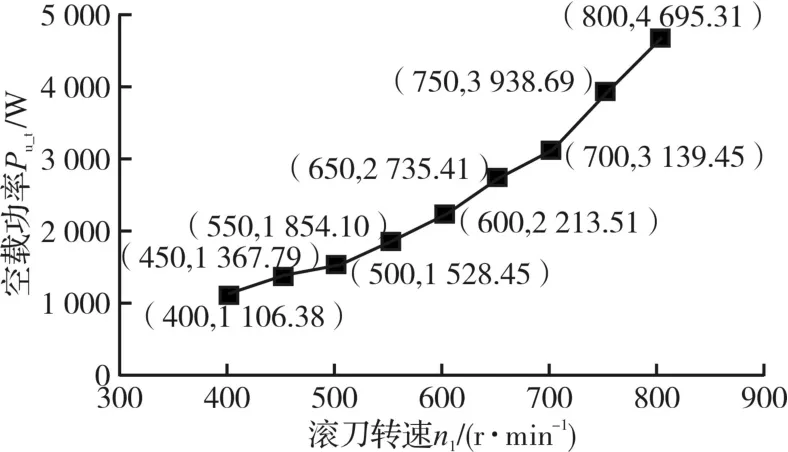
图4 不同转速下的刀具轴空载功率Fig.4 The tool axis no-load power under different speed

结合机床基础数据（表4）和辨识得到的参数，以及加工参数（表5），分别按照刀具轴载荷损耗计算公式和工件轴载荷损耗系数计算公式得两组载荷损耗系数，结果如表6所示。

表6 载荷损耗系数值Tab.6 The value of load loss coefficient

应用HIOKI-3390C功率仪测量滚齿机床按加工转速空转时的工件轴输入功率，即空载功率Pu_w，测量加工过程中刀具轴和工件轴的实时输入功率Pin_t、Pin_w，应用HC-33C3多路组合型三相电测量终端测量加工过程中机床总输入功率PM_in，由式（48）、式（49）分别算得滚齿机刀具轴和工件轴的瞬时切削功率Pc_t、Pc_w。图5a所示为加工一个工件的切削功率曲线。从图5a可以看出：根据国内某机床厂总结出的滚削力计算公式推导而来的平均滚削功率经验公式为

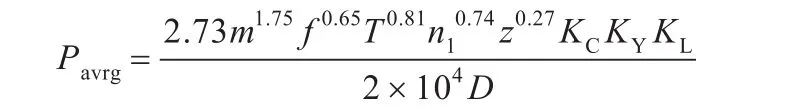
式中，T为吃刀深度，T=λ/(2.25m)；KC为工件材料修正系数，查表取1.24；KY为工件硬度修正系数，查表取1.05；KL为螺旋角修正系数，查表取1.11。

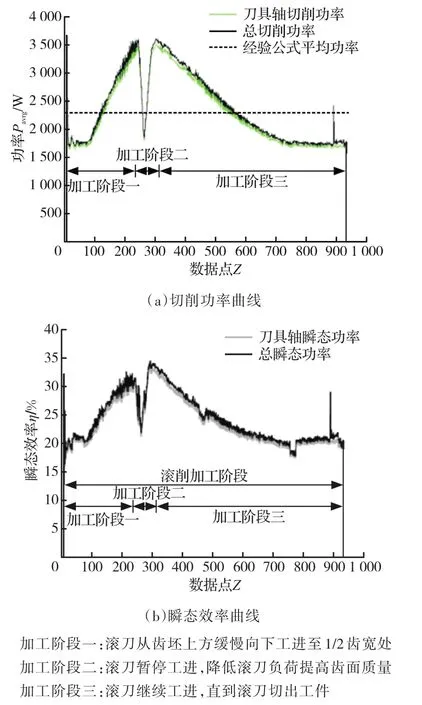
图5 切削功率及瞬态效率曲线Fig.5 The curve of cutting power and instantaneous efficiency

计算得到的平均功率为定值，无法反映机床的实时加工状态，而本文的载荷损耗系数计算获取法能够直观地反映机床的实时加工情况，更具实用性，尤其适用于刀具工件双旋转运动机床的能量效率监控系统。

根据瞬态能量效率计算模型得到刀具工件双旋转运动机床加工一个完整工件的瞬态能量效率，如图5b所示，该曲线直观反映了机床的实时能效状况，间接反映了机床的各个加工阶段。

根据本文提出的刀具工件双旋转运动机床计算获取的滚齿机能量效率Ψ1=17.18%，与经验公式计算结果的能量效率（Ψ3=16.78%）的误差为0.4%＜5%；在只考虑刀具轴输出功率的情况下，计算得到的滚齿机床能量效率为Ψ2=16.70%，与经验公式计算结果的误差为0.08%＜5%，说明本文提出的能量效率获取方法的准确性可以接受。本文提出的能量效率获取方法较仅考虑刀具轴有效功率的情况下计算得到的能量效率值精度更高，能够更好地用于刀具工件双旋转运动机床的能量效率获取，因此，本文提出的方法能够用于刀具工件双旋转运动机床的能量效率获取。

5 结论

针对刀具工件双旋转运动机床的能量效率难于获取的难题，本文对刀具工件双旋转运动机床的能量效率获取方法进行了研究。提出了一种运用载荷损耗系数计算获取刀具工件双旋转运动机床能量效率的方法。实际应用时，通过安装功率传感器测取加工过程中的输入功率和空载功率，并结合上述计算模型便可长期有效地获取刀具工件双旋转运动机床的能量效率。

实验验证和应用案例研究结果证实了本文方法的准确性、可行性和实用性。该方法无需安装切削力测量仪器，弥补了现有能量效率获取方法中切削仪器安装困难、理论公式复杂且难以反映实时能效状况等不足，解决了刀具工件双旋转运动机床能量效率难以获取的问题。该方法可为机床能效预测、监控与管理提供技术支撑，具有较广阔的应用前景。

参考文献：

［1］ 刘飞，刘培基，李聪波，等.制造系统能量效率研究的现状及难点问题［J］.机械工程学报，2017，53（5）：1-11.

LIU Fei，LIU Peiji，LI Congbo，et al.The Statue and Difficult Problems of Research on Energy Efficiency of Manufacturing Systems［J］.Journal of Mechanical Engineering，2017，53（5）：1-11.

［2］ European Commission.2030 Climate&Energy Frame⁃work［EB/OL］.［2017-06-14］.http：//ec.europa.eu/cli⁃ma/policies/strategies/2030/index_en.htm.

［3］ America Energy Department.Clean Energy Manufac⁃turing Innovation Institute［EB/OL］.［2017-06-14］.http：//www.energy.gov/articles/energy-department-an⁃nounces-70-million-innovation-institute-smart-manu⁃facturing.

［4］ VIJAYARAGHAVAN A，DORNFELD D.Automated Energy Monitoring ofMachine Tools［J］.CIRP Annals—Manufacturing Technology，2010，59（1）：21-24.

［5］ ALTINTAŞ R S，KAHYA M，ÜNVER H Ö.Modelling and Optimization of Energy Consumption for Feature Based Milling［J］.International Journal of Advanced Manufacturing Technology， 2016， 86 （9/12） ：3345-3363.

［6］ LEE J Y，SHIN Y J，KIM M S，et al.A Simplified Machine-tool Power-consumption Measurement Procedure and Methodology forEstimating Total Energy Consumption［J］.Journal of Manufacturing Science&Engineering，2016，138（5）：051004-9.

［7］ ABELE E，SIELAFF T，SCHIFFLER A，et al.Analyz⁃ing Energy Consumption of Machine Tool Spindle Units and Identification of Potential for Improvements of Efficiency［M］//Glocalized Solutions for Sustainability in Manufacturing.Berlin：Springer Berlin Heidel⁃berg，2011：280-285.

［8］ SAJ.JIS TS B 0024-1：2010 Machine Tools-test Meth⁃ods for Electric Power Consumption—Part 1：Machin⁃ing Centers［S］.Japanese Standards Association，2010.

［9］ ISO.ISO/WD14955-1.Environmental Evaluation of Ma⁃chine Tools-Part1：Energy-saving Design Methodolo⁃gy for Machine Tools［S］.International Organization for Standardization，2010.

［10］ LENZ J，KOTSCHENREUTHER J，WESTKAEMPER E.Energy Efficiency in Machine Tool Operation by Online Energy Monitoring Capturing and Analysis［J］.Procedia Cirp，2017，61：365-369.

［11］ 刘高君，刘飞，刘培基，等.机床多源能耗状态在线检测方法及检测系统［J］.计算机集成制造系统，2016，22（6）：1550-1557.

LIU Gaojun，LIU Fei，LIU Peiji，et al.On-line Detect⁃ing Method and System of Multi-source Energy State for Machine Tools［J］.Computer Integrated Manufac⁃turing Systems，2016，22（6）：1551-1558.

［12］ GUTOWSKI T G，BRANHAM M S，DAHMUS J B，et al.Thermodynamic Analysis of Resources Used in Manufacturing Processes［J］.Environmental Science&Technology，2016，43（5）：1584-1590.

［13］ KARA S，LI W.Unit Process Energy Consumption Models for Material Removal Processes［J］.CIRP Annals—Manufacturing Technology，2011，60（1）：37-40.

［14］ LIU F，WANG Q，LIU G.Content Architecture and Future Trends of Energy Efficiency Research on Machining Systems ［J］.JournalofMechanical Engineering，2013，49（19）：87.

［15］ HU S，LIU F，HE Y，et al.An On-line Approach for Energy Efficiency Monitoring of Machine Tools［J］.Journal of Cleaner Production，2012，27（6）：133-140.

［16］ VELCHEV S，KOLEV I，IVANOV K，et al.Empirical Models for Specific Energy Consumption and Optimi⁃zation of Cutting Parameters for Minimizing Energy Consumption during Turning［J］.Journal of Cleaner Production，2014，80：139-149.

［17］ 刘培基，刘霜，刘飞.数控机床主动力系统载荷能量损耗系数的计算获取方法［J］.机械工程学报，2016，52（11）：121-128.

LIU Peiji，LIU Shuang，LIU Fei.Calculating Method for Additional Load Loss Coefficient of Spindle Sys⁃tem of CNC Machine Tools［J］.Journal of Mechani⁃cal Engineering，2016，52（11）：121-128.

［18］ 王秋莲，刘飞.数控机床多源能量流的系统数学模型［J］.机械工程学报，2013，49（7）：5-12.

WANG Qiulian，LIU Fei.Mathematical Model of Multi-source Energy Flows for CNC Machine Tools［J］.Journal of Mechanical Engineering，2013，49（7）：5-12.

［19］ CAI W，LIU F，XIE J，et al.An Energy Management Approach for the Mechanical Manufacturing Industry through Developing a Multi-objective Energy Bench⁃mark［J］.Energy Conversion&Management，2017，132：361-371.

［20］ HU S，LIU F，HE Y，et al.Characteristics of Addition⁃al Load Losses of Spindle System of Machine Tools［J］.Journal of Advanced Mechanical Design Systems&Manufacturing，2010，4（7）：1221-1233.

［21］ 刘飞，徐宗俊，但斌，等.机械加工系统能量特性及其应用［M］.北京：机械工业出版社，1995.

LIU Fei，XU Zongjun，DAN Bin et al.The Energy Characteristics of Machine Tool's System and Its Application［M］.Beijing：China Machine Press，1995.

［22］ 邓加凌，朱劲.通用交流伺服驱动器的功耗与效率估算［J］.科技创新导报，2009（35）：29-30.

DENG Jialing，ZHU Jin.Estimation of Power and Effi⁃ciency for General AC Servo Drives［J］.Science and Technology Innovation Herald，2009（35）：29-30.

［23］ VAVRUS V，RADVAN R，RAFAJDUS P.A Power Loss Calculation Method of IGBT SRM Converter［C］//International Conference on Electrical Drives and Power Electronics.Tatranska Lomnica，Slovakia：IEEE，2015：521-526.

［24］ 张明元，沈建清，李卫超，等.一种快速IGBT损耗计算方法［J］.船电技术，2009，29（1）：33-36.

ZHANG Mingyuan，SHEN Jianqing，LI Weichao，et al.Calculation Method of a Fast Power Loss for IGB Tmodules［J］.Marine Electric&Electronic Engineer⁃ing，2009，29（1）：33-36.

［25］ 刘德林，赵瑞杰，代兴华，等.2MW风电变桨伺服驱动器IGBT损耗计算及散热系统设计［J］.电气传动，2015，45（10）：71-75.

LIU Delin，ZHAO Ruijie，DAI Xinghua，et al.Losses Calculation of IGBT Module and Heat Dissipation System Design of Servo Driver for Pitch Control of 2MW Wind Power［J］.Electric Drive，2015，45（10）：71-75.

［26］ 胡韶华.现代数控机床多源能耗特性研究［D］.重庆：重庆大学，2012.

HU Shaohua.Energy Consumption Characteristics of Multiple-component of Modern CNC Machine Tools［D］.Chongqing：Chongqing University，2012.

（编辑 袁兴玲）

作者简介：张西成，男，1991年生，硕士研究生。研究方向为机床能量效率。E-mail：xc_zhang@cqu.edu.cn。刘 飞（通信作者），男，1948年生，教授、博士研究生导师。研究方向为绿色制造、制造系统工程和数字化制造。E-mail：fliu@cqu.edu.cn。