运行和方差控制图的改进

杨 静，宋向东，张雪芳，焦博雅

（燕山大学 理学院，河北 秦皇岛 066004）

0 引言

控制图被看作是统计过程控制（SPC）中最有效的工具之一，用于监控过程参数和检测生产过程是否处于受控状态。检测过程方差与检测过程均值一样重要。过程方差的增加会导致产品质量的降低，过程方差的降低意味着生产水平的提高，可能预示了未来产品质量的提高。当前最普遍使用的检测过程方差的控制图是休哈特（Shewhart）R图，S图和S2图。众所周知，传统的休哈特控制图只对大偏移敏感，对小的和中等的偏移不敏感，另外它们在样本容量很小时，检测过程工艺提高的效率低下。

为了克服这些缺点，一些学者提出和研究了带有运行规则的检测过程方差的控制图，之后Reynolds进行了进一步的研究。起初，它的提出是用于检测过程均值。Jaehn[1]提出了运行和控制图的一个特例，控制图在中心线上下各划分四个区域，把这种控制图叫做区域控制图。Davis等[2]研究了区域控制图的改进。Champhe和Rigdon[3]用马尔科夫链方法分析了运行和图平均链长的分布。Rakitzis和Antzoulakos[4]提出的监测过程方差的运行和控制图。Schoonhoven[5]研究和分析了带估计参数的标准差控制图。文献[6]和文献[7]介绍了运行和控制图中的其他研究工作。郝惠娟[8]改进了基于对数方差的累积和控制图，设计了可变抽样区间累积和方差控制图。薛丽[9]提出了可变抽样区间的二项变量累积和控制图。张斌和周伟灿等[10]针对过程异常导致均值和标准差同时发生漂移的情况，考虑田口质量损失、抽样成本等，构建了综合损失模型，提出了可变抽样区间X-R图优化设计方法。本文在前人研究基础上，给出不同区域划分，设计了加入-1得分的单边运行和方差控制图，并研究其平均链长表现。

1 单侧运行和方差控制图（RSS）设计及平均链长的计算

1.1 传统S图

Xij为来自质量特性值X的样本容量为n的第i个随机样本的第 j个观测值。第i个样本的样本均值和样本标准差分别为：

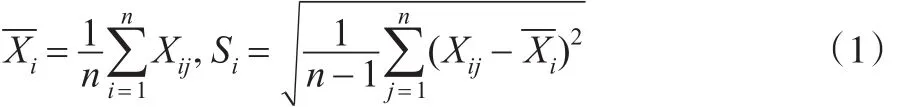
假定样本独立，且质量特性值X服从正态分布，其受控下标准差为σ0（假设X的均值一直保持在目标值，且不失一般性本文采用σ0=1），一个失控的标准差值记作σ1=τσ0(τ＞0)。 τ＞1和 0＜τ＜1分别对应过程标准差的增加和减少。对于τ=1代表过程处于受控状态。

对于传统的双边S图，随着样本数量i，统计量Si它的统计设计需要一对控制线的设定：一个上控制线UCL和一个下控制线LCL，对于单边S图则只需要上控制线UCL。由于S统计量的偏斜，一些研究者提倡使用概率极限，以此代替传统的3σ极限。因此对于错误警报率为a的单边S图，上控制限为（其中 χ2n-1;a代表自由度为n-1的卡方分布的上a分位点）。一旦有观测点落在控制限外，即Si＞UCL，表明过程方差可能增加，与之对应的生产过程变差。

控制图常用的一个评价指标是它的平均链长（ARL）。对于一个过程参数给定偏移的情况，ARL是直到发生报警那一刻样本点落在控制图上的平均数量。在休哈特控制图中，ARL=1/p，p是一个点落在控制限之外的概率。因此当过程标准差偏移σ1=τσ0(τ＞1)，单边有上限的控制图失控的ARL（记作ARL1）可由如下P计算：

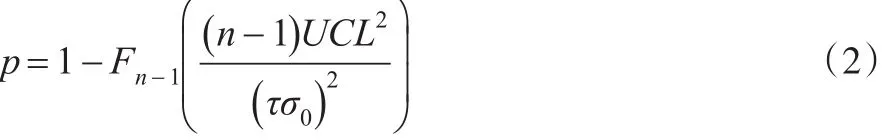
1.2 单边的运行和方差控制图及ARL计算

单边的运行和方差控制图需要把传统单边S图分为若干个区域，对每个区域给定一个得分，统计量落在哪个区域则累加相应得分，当累积得分超过一个规定值，控制图就会发生失控信号。本文只研究把单边控制图划分为四个区域的情况，这也是其他学者们研究最多的情况，被称作是区域控制图。在单边控制图中加入3个上控制线，UCL1＜UCL2＜UCL3。其中：

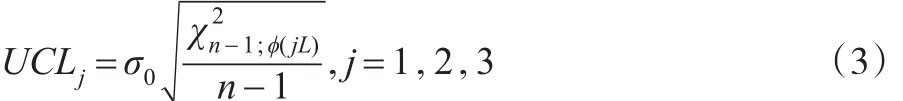
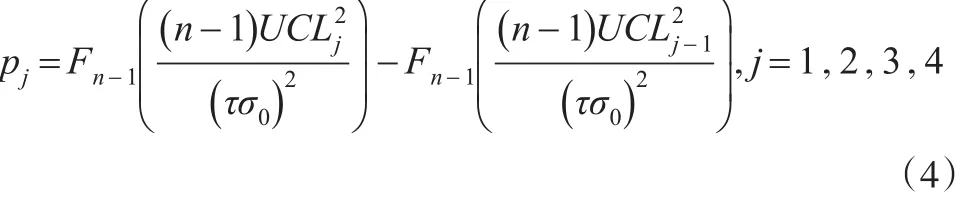
本文把包含四个区域，得分分别为 a1，a2，a3，a4，决策值为 H 单边的运行和方差控制图记为 RSSH(a1，a2，a3，a4)。划分区域，对应得分以及概率如表1所示。

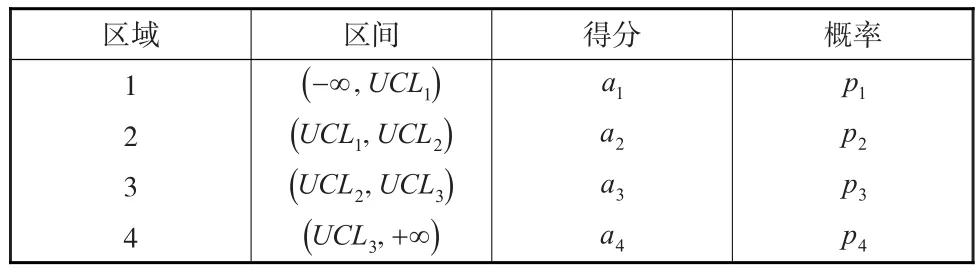
表1 RSSH（a1，a2，a3，a4 ）的区间划分，对应得分及概率

由表1可得得分与观测值对应函数：

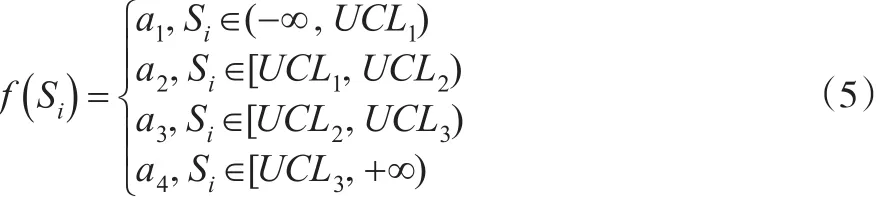
对于单边运行和控制图的检验，基于统计量：

其中i=1，2，…，j=1，2，3且C0≥0。C0的初始值取决于是否加入初始响应。单边的控制图报警当Ci≥H，其中H是一个合适的决策值。显然，累积得分取正整数值0，1，2…，H 。过程的初始状态记为 E0；若Cn=i，则称过程处于Ei；若Ci≥H，则称过程处于吸收态EH得到状态空间后，求得每个状态的一步转移概率Pij=P(Cn+1∈Ej|Cn∈Ei)，得到一步转移概率矩阵：

其中R为P除去最后一行最后一列得到的矩阵，I为H维单位阵，1为元素全为1的H维列向量。根据以下公式（8）可以求出ARL值。

RSSH（a）1，a2，a3，a4的控制限的决定仅仅取决于 L值的选择，而L值得选取是根据预期设定的ARL0水平，记为c。因此，对于RSSH（a）1，a2，a3，a4的统计设计，建议步骤如下：

步骤2：设定 ARL0=c；

步骤3：根据ARL0=c计算合适的L值；

步骤4：在第i个样本，如果Ci＞H，则判定过程失控。

假设受控下分布服从标准正态分布，标准差偏移倍数τ从1到2.5，求得带有不同得分的运行和方差控制图（RSS）的ARL，结果见表2所示。

表2中数据分别是取受控状态下ARL0为370时，标准差偏移倍数从1.0到2.5时，运行和方差控制图RSS14(-1，1，6，12),RSS20(-1，2，7，13),RSS20(-1，2，7，14),RSS20(-1，3，4，12),RSS16(-1，2，3，8),RSS30(-1，3，8，15),RSS42(-1，3，11，19)的ARL值。本文选取其中检测效率最高的RSS14(-1，1，6，12)控制图进行以下研究。

表2 不同参数运行和方差控制图的ARL表现(ARL0=370，n=5)

2 运行和方差控制图和其他控制图的比较

2.1 与现有运行和方差控制图的比较

对比现有的运行和方差控制图，本文给出了不同区域得分以及门限值的参数设置方法。令受控下的平均链长均为370，当方差偏移倍数从1.1到2.5时，现有参数设置的平均链长表现与本文中平均链长的表现对比结果如图1所示。

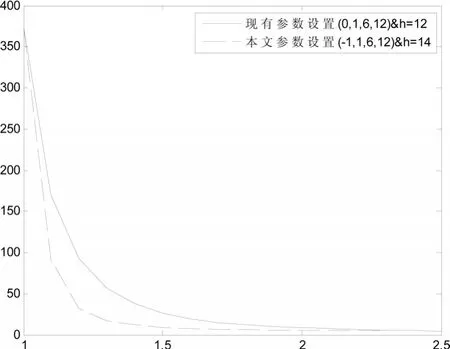
图1 本文参数设置效果

可以看出，受控下平均链长均为370时，标准差偏移倍数从1.1到2.5时，本文参数设置方法产生的运行和方差控制图的平均链长明显小于现有参数设置的运行和方差控制图，可以更快地发现生产过程中的质量变化，检测效率显著提高。

2.2 与累积和控制图的比较

2.2.1 累积和控制图计算原理

先用样本方差s2来估计总体方差σ2。假定所有观测值都服从正态分布，且相互独立，其中总体均值相同，即xi～N(μ0，σ2)，f为概率密度函数，考虑如下假设检验问题：

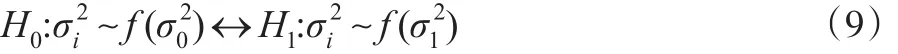
原假设H0成立时，所有的样本都来自相同的分布，此时方差波动在控制范围内，过程处于受控状态。备择假设H1成立说明方差波动不在控制范围内，过程失控。由统计学知识，样本方差 s2服从伽马分布，概率密度函数为：

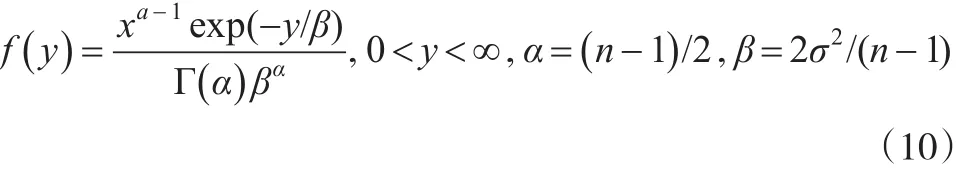
利用序贯概率比的基本方法对过程方差进行检验，似然比统计量为：

令λn＞A来对过程异常做出判断，对上式两边取对数得：

由上式可以定义检验过程方差向上漂移的CUSUM统计量：

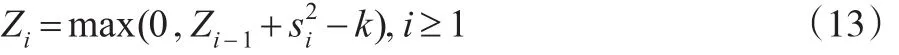
2.2.2 运行和方差控制图与累积和控制图效果对比

根据检验过程方差向上漂移的CUSUM的以上参数设置，用matlab软件进行万次随机模拟，可求出当受控下平均链长约为370时，标准差偏移倍数从1.1到2.5时，CUSUM控制图的平均链长。图2为过程标准差在不同偏移倍数下运行和方差控制图和CUSUM控制图的平均链长对比结果。

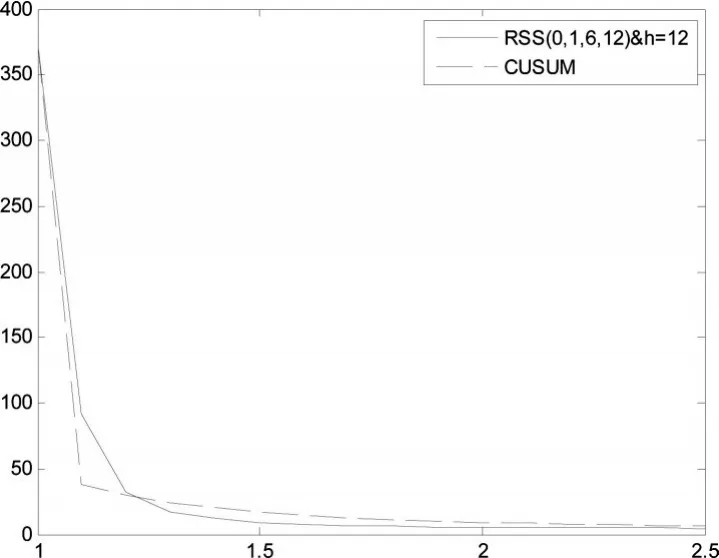
图2 RSS与CUSUM效果对比

由图2可以看出，当标准差偏移倍数从1到2.5时，运行和方差控制图相比CUSUM平均链长表现并没有明显的优越性。

3 加入初始响应的运行和方差控制图与累积和控制图的比较

初始响应特性（fast initial response，FIR），在CUSUM控制图对过程是否处在受控状态的判定中显示出良好的效果。因此，通过加入初值响应的方法改进RSS控制图，以提高其检测效率。初始响应值记为S1，以下是RSS14(-1，1，6，12)分别加入7和10的初值响应，对CUSUM分别加入0.25H，0.5H和0.75H时，各控制图的运行链长表现，见表3所示。

表3 加入FIR后RSS与CUSUM效果对比

从表3可以看出，当方差无偏移时ARL近似相等情形下，初始响应值分别为7和10的RSS控制图相比带有0.25H，0.5H，0.75H的CUSUM控制图，在标准差偏移倍数在1到1.3时，RSS检测效率不如CUSUM。在标准差偏移倍数大于1.3时，RSS检测效率均优于CUSUM控制图，说明设计的运行和方差控制图在检测中等偏移和大偏移时具有优越性。

4 结论

本文对检测向上漂移的单侧运行和方差控制图进行了不同的参数设计，利用马尔科夫链方法近似计算控制图的平均链长，运行链长结果显示本文参数设置相比现有的运行和方差控制图的参数设置，检测效率明显提高。但RSS控制图相比于CUSUM控制图，效果不具有明显优越性。因此，本文对RSS和CUSUM分别加入不同的初始响应值，运行链长结果显示，对于方差不同倍数的偏移，RSS在检测中等偏移和大偏移时具有优越性。鉴于RSS控制图比CUSUM实施步骤简单易操作，但其检测效果可与CUSUM相媲美，因此运行和方差控制图具有实际可行性。它的进一步研究是有实际意义的。

参考文献：

[1]Jaehn A H.The Zone Control Chart[J].Quality Progress,1991,24(7).

[2]Davis R B,Jin C,Guo Y Y.Improving the Performance of the Zone Control Chart[J].Communication in Statistics-Theory and Methods,1994,23(12).

[3]Champ C W,Rigdon S E.An Analysis of the Run Sum Control Chart[J].1997.

[4]Rakitzis A C,Antzoulakos D L.Run Sum Control Charts for the Monitoring of Process Variability[J].Quality Technology&Quantitative Management,2016,13(1).

[5]Schoonhoven M,Riaz M,Does R J M M.Design and Analysis of Control Charts for Standard Deviation With Estimated Parameters[J].Journal of Quality Technology,2011,43(4).

[6]Acostamejia C A,Rincon L.The Continuous Run Sum Chart[J].Political Communication,2014,43(20).

[7]Wei L T,Khoo M B C.A Study on the Run Sum X-bar Control Chart With Unknown Parameters[J].International Conference on Aip Conference,2012,1482(1).

[8]郝惠娟.基于可变抽样区间的累积和方差控制图研究[J].数学的实践与认识,2013,43(6).

[9]薛丽.可变抽样区间的二项变量累积和控制图设计[J].统计与决策,2016，(9).

[10]张斌,周伟灿,费文龙.基于质量损失函数的可变抽样区间X-R图优化设计[J].统计与决策,2011，(1).