基于半参数估计的非随机缺失样本分类

夏利宇，王 蕾，刘赛可

（中国人民大学 应用统计科学研究中心，北京100872）

0 引言

因变量非随机缺失在统计应用领域较为常见，例如信用评级领域的拒绝推断难题、市场营销中无偏好客户的不响应问题、微观调查中敏感问题的无回答现象等。实践中，相比样本中的完备数据，人们对非随机缺失数据分析更感兴趣，例如预测贷款客户违约概率、不响应客户的消费偏好、无回答者的真实特征，这可以拓展业务领域和研究范围，往往能成为创造经济利益和解答关键问题的途径。学界中，非随机缺失问题因为样本的删失结构破坏了其他完备样本对总体的代表性，进而导致参数估计的有偏与非一致而受到普遍关注。引入数据缺失机制来预测非随机缺失样本的特征，解决样本代表性偏差带来的问题，探寻效果优良的统计模型对非随机缺失数据分析至关重要。

Rubin（1976）[1]根据因变量和自变量对因变量缺失的影响，将缺失机制分为随机缺失(MAR)、完全随机缺失(MCAR)和非随机缺失(MNAR)三类。在MAR和MCAR情况下，因变量缺失与其自身无关，可以直接删除含缺失数据的样本推断总体性质；而在MNAR情况下，因变量缺失与其自身有关，建模时必须考虑数据的缺失机制。Graham和Donaldson（1993）[2]证明，直接删除非随机缺失样本建模将导致参数估计的有偏与非一致，填补非随机数据后，建模效果将显著提升。Heckman（1979）[3]提出了处理因变量非随机缺失的Heckman两步法，通过两个Probit模型还原了样本选择过程和结果发生过程，该方法思路清晰，但在实际应用中效果不佳。Banasik和Crook（2007）[4]详细说明了处理非随机缺失问题的扩张法，该方法因假定缺失数据与非缺失数据具有相同的数据分布而无法得到学界的广泛认可。

本文将借鉴Kim和Yu（2011）[5]非随机缺失数据均值泛函估计的思想，将其一元核函数拓展成多元核函数，运用基于指数倾斜的半参数模型预测样本属于各类的发生概率，解决MNAR情形下的样本二分类问题。

1 研究方法

1.1 非随机数据的半参数估计模型

非随机缺失数据均值泛函的半参数估计方法因其非参数部分而具有稳健性，结合实际应用的要求，本文将其模型中一元协变量的设定调整为多元协变量。

(x1i,…,xpi,yi),i=1,…,n 是随机变量 (X1,…,Xp,Y)的样本，其中，yi是可能缺失的因变量，(x1i,…,xpi)是总可以被观测到的协变量，n为样本容量，p为协变量个数。τi是示性函数，服从响应概率为πi(x1i,…,xpi,yi)的Bernoulli分布，当 τi=1 时，yi可观测，当 τi=0 时，yi缺失。τi=1时，yi的条件密度是时，yi的条件密度是 f0（yi|x1i,…,xpi）。 K(∙)是核密度函数，其窗宽是h，满足当n→∞时，h→0,nh→∞。本文中采用高斯核密度函数，其最优窗宽为h=xn-1/(p+4),x为 xi的标准差。

当πi与 yi独立时，缺失机制是MAR，此时：

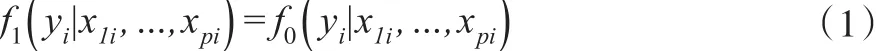
当πi与 yi相关时，缺失机制是MNAR，此时的条件密度关系为：

其中，O(x1i,…,xpi,yi)是优势比函数，形式为：

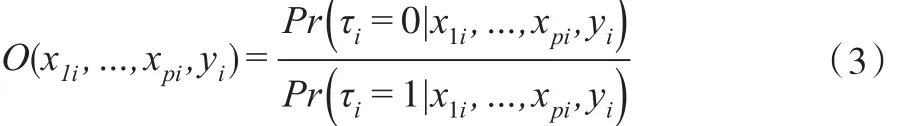
假定响应概率πi来自服从Logit分布的半参数模型，即：

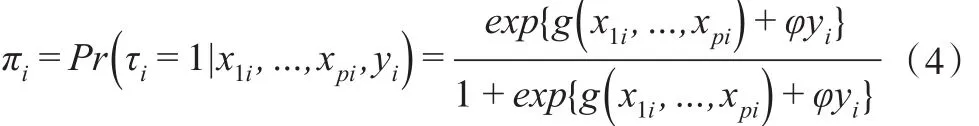
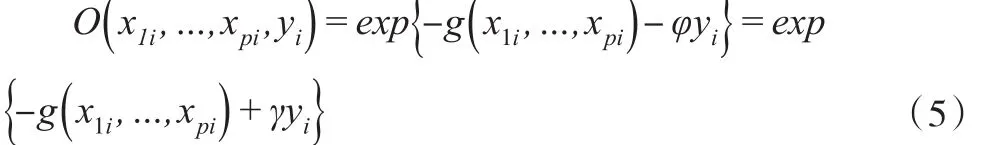
进而式（2）条件密度关系可以表示为：

式（6）称为指数倾斜模型，γ为倾斜参数，表明非随机缺失机制对随机缺失机制的偏离程度。在实际问题中，γ一般未知，可通过独立调查或验证样本来估计。

对于可观测的样本，其非参数估计m1（x1i,…,xpi）=可通过最小化式（7）求得其估计值，其中是权重。

可以证明：

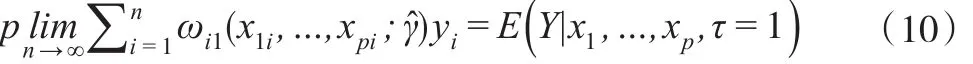
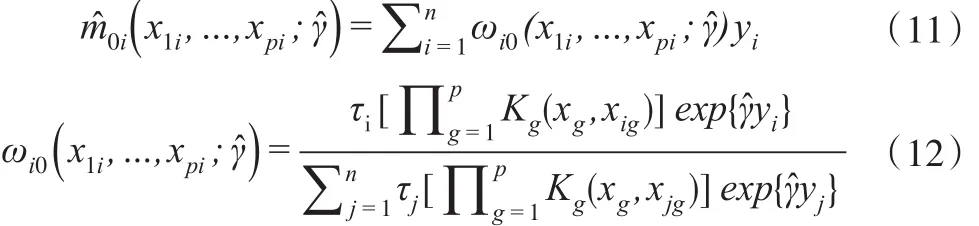
可以证明：

基于指数倾斜的半参数模型在估计中引入了因变量非随机缺失的机制，借助非参数模型兼具灵活性和可解释性的优势，以广义非参数模型估计倾斜参数γ，获得因变量均值的一致估计。可以利用式（11）获得τi=0时 yi的估计值。结合式（11），当 yi是二分类变量时，yi=1的预测概率为，yi=0的预测概率为1-，当＞0.5 时，可预测样本属于 yi=1 的一类，反之属于yi=0的一类。

1.2 分类评价标准

对于非随机缺失数据的二分类问题，不同类别的误判成本往往存在较大差别，例如信用评级中误判违约客户的成本大于误判履约客户的成本，因此，在二分类模型优劣的评价中仅仅考虑整体分类精度是不够的，需要根据误判成本差异同时参考其他评价指标。本文考察分类模型的精度(Accuracy)、召回率call(Recall)、准确率(Precision)、G 均值(G_mean)、Fβ得分(Fβ_Score)：

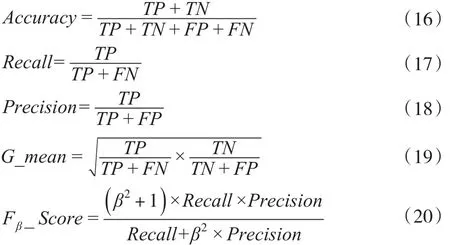
其中，TP、TN、FP、FN分别是混淆矩阵中的真正、真负、假正、假负。Accuracy表示模型正确预测非随机缺失样本的比例，Recall表示所有高误判代价样本被正确预测的比例，Precision表示被正确预测为高误判代价样本的比例，G_mean表示高误判代价样本和低误判代价样本被正确预测比例的几何平均数，Fβ_Score表示由参数β调整指标Recall和Precision的组合，β反应指标的相对重要性。本文对模型优劣的判断主要依据Recall、G_mean、F1_Score和 F2_ScoreFβ_Score。

2 数值模拟

情形1：

情形2：

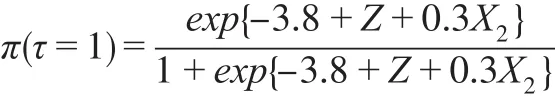
情形3：

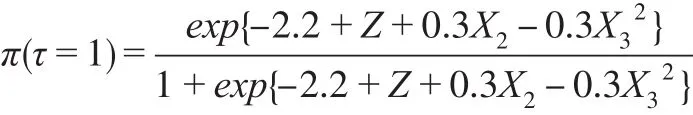
情形4：

情形5：

情形6：

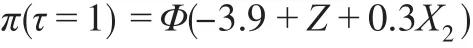
情形7：

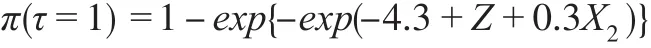
情形8：

其中，Φ(∙)是标准正态分布的累积密度函数。以上8类因变量缺失情形中，情形1是随机缺失，其他情形是非随机缺失。设定样本容量n=1000，每类缺失情形重复模拟100次，以消除随机性。半参数模型中γ的估计，首先利用可观测数据建立非参数模型，粗略估计非随机缺失样本的分类插补到原始数据中构成完备数据，然后根据式（4），利用完备数据建立广义半参数模型，得到参数估计值为对比半参数模型的分类效果，本文同时建立Logit模型、SVM模型和决策树模型对非随机缺失样本进行分类，计算模型在各类缺失情形下评价指标的均值，数值模拟结果如表1。

当样本随机缺失（情形1）时，半参数模型的召回率和F1得分在四个模型中最大，但其G均值和F2得分仅优于决策树模型，预测精度不及Logit模型和SVM模型，半参数模型的分类效果没有显著优势。当样本非随机缺失（情形2—情形8）时，半参数模型的精度、召回率、G均值、F1得分在四个模型中最大，除情形3和情形5外，其F2得分在四个模型中也最大，半参数模型的分类效果明显优于其他其他三个模型。在情形3和情形5中，由于决定π的模型中有平方项X32和交互项X2Z，他们提升了协变量X对π的影响，降低了潜变量Z对π的影响，在此二类情形下，半参数模型的F2得分低于Logit模型。综合各类非随机缺失情形的指标值，除本文的半参数模型外，Logit模型的分类效果优于SVM模型和决策树模型，这可能是非随机缺失的机制设计上假定响应概率服从Logit分布或正态分布。模拟研究表明，本文的半参数模型并不适合因变量随机缺失情形下样本的分类，但该模型是处理非随机缺失样本分类的有效方法。

表1 数值模拟结果

3 实证

实证数据来源于 BankScope数据库，它是 BνD(Bureau νan Dijk)与评级机构惠誉(FitchRatings)合作开发的银行信息数据库，提供全球主要银行及重要金融机构的经营与信用数据。本文的研究内容是通过银行的主要财务指标对银行经营状态非随机缺失的样本进行分类，将经营状态分为“正常”(Y=1)和“异常”(Y=0)二类，“正常”指银行当前正在经营，“异常”指银行撤并、解散或倒闭等。协变量选择总资本比率(X1)、贷款损失准备金/贷款总额(X2)、股东权益/总资产(X3)三个指标。决定其是否缺失的潜在变量选择存款及短期资金(T1)、所有者权益(T2)、净利息收益率(T3)。

对原始数据进行筛选和整理后，建模数据的样本容量为1115，其中正常银行769家，异常银行346家。设定因变量非随机缺失的比例为30%，将潜在变量标准化，令，Z0.3是Z的30%分位数，当 Zi＜Z0.3时，第 i家银行经营状态缺失(τi=0)。因为缺失状况根据ε的随机性而不同，故重复此缺失机制100次。结合BankScope数据库中的真实数据，建立半参数模型、Logit模型、SVM模型和决策树模型，计算各类分类评价指标的均值，结果见表2。

表2 实证结果

结合银行真实数据的实证研究结果表明，当缺失机制不是由Logit分布或正态分布决定时，半参数模型的召回率、G均值、F1得分、F2得分在四个模型中仍最大，分类效果最佳，这说明半参数模型对于更复杂的非随机缺失机制具有良好的适应性。相比之下，由于缺失机制分布的改变，决策树模型的分类效果明显优于Logit模型和SVM模型。

4 结论

本文主要应用基于指数倾向的半参数模型解决非随机缺失样本的二分类问题，引用均值泛函的半参数方法估计样本属于某一类别的概率。模拟研究表明，与Logit模型、SVM模型、决策树模型相比，本文的半参数方法对于随机缺失样本的分类效果欠佳，但在处理非随机缺失样本的二分类问题上有明显优势，对处理非随机缺失问题具有针对性。实证研究表明，半参数模型对处理实际问题中非随机缺失样本的二分类问题同样具有适用性。

由于模型中使用了核函数建模，当样本容量过小或数据中有异常值时，分类效果可能会受到影响。在本文的研究中，协变量均为数值型变量，协变量间相互独立，并未对模型中的特征选择问题进行研究。在未来的研究中，可以考虑协变量为定性变量且协变量间相关的情况，讨论适合非随机缺失样本分类的半参数模型的特征选择方法，并将二分类模型向多分类模型拓展。

参考文献：

[1]Rubin D B.Inference and Missing Data[J].Biometrika,1976,(63).

[2]Graham J W，Donaldson S I.Evaluating Interventions With Differential Attrition:The Importance of Nonresponse Mechanisms and Use of Follow-up Data[J].Journal of Applied Psychology,1993,(78).

[3]Heckman J J.Sample Selection Bias as a Specification Error[J].Econometrica,1979,(47).

[4]Banasik J,Crook J.Reject Inference,Augmentation and Sample Selection[J].Eur J Opl Res,2007,(183).

[5]Kim J K，Yu L C.A Semi-parametric Estimation of Mean Functionals With Non-ignorable Missing Data[J].Journal of the American Statistical Association,2011，(106).