休哈特控制图的改进

宋向东, 杨 仪

(燕山大学 理学院 河北 秦皇岛 066004)

休哈特控制图的改进

宋向东, 杨 仪

(燕山大学 理学院 河北 秦皇岛 066004)

在常规控制图的基础上提出了“平均链长(ARL)无偏的常规控制图”及“控制图的ARL无偏性质”. 首先, 通过利用样本的分布函数精确求解出标准差, 获得控制图的上下控制限. 然后比较ARL无偏控制图和常规控制图在监控生产过程中的质量变化. 最后结合数值算例, 得出ARL无偏控制图在监控生产过程中和质量变化时更具有优势.

休哈特R控制图； 休哈特s控制图； 平均链长； 概率分布函数

0 引言

在研究中往往假设常规控制图R图和s图都是近似正态分布, 在实际问题中, 样本的极差R和标准差s都是从0开始趋近无限大, 在控制图的右侧无限延长且趋近于零. 当α=0.002 7 时, 在许多情况下R和s控制图平均链长最大值不是370, 这种缺陷在小样本检测中更加明显,原因在于监控生产过程中R和s图的最小值均是从0开始, 去掉了负数部分的下控制限,使整个控制图呈偏态分布的.

为了克服这些问题, 文献[1]提出了一种改进的R图(IRC).文献[2]讨论了常规s图的不足, 提出了一种修正的s控制图.文献[3]研究了高产过程的 CCC-r控制图.文献[4-6]提出了多种改进的常规控制图.文献[7]展示了改进的R和s控制图(IRC和ISC),通过计算顺序统计量的分布函数得到IRC和ISC.本文在文献[7]的基础上, 通过定义无偏的平均链长, 得到了ARL无偏的R(UBRC)和s(UBSC)控制图, 并精确计算控制图的上下限的参数.

定义1 对于某个同时具有上下控制限的控制图, 若σ=1时，平均链长达到最大；当σ偏离标准值1时，平均链长变小, 则称该控制图为ARL无偏的.否则称该控制图为ARL有偏的.

1 ARL无偏的R和s控制图

1.1 ARL无偏的R控制图

假设X服从独立同分布的标准正态分布N(μ,σ2)，已知其均值μ和标准差σ0.有一组大小为n的样本,对这些样本进行排序得到x(1),x(2),…，x(n).标记σ为过程标准差,其标准值为σ0.设0<λ<∞，用λσ0表示系统偏移量,当λ=1时表示无偏移.

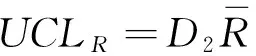
R控制图的上下控制限UCLR和LCLR分别表示为[7]

(1)

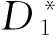
(2)

(3)

ARL无偏的R控制图的平均链长为LR(λ)=1/p(λ),当λ=1时,平均链长L(λ)取极大值L(1)=370.398 3，即发出失控信号的概率为p(λ),当λ=1时得到极小值.当λ=1时,由方程(3)整理可得

(4)

其中g,G分别为R图的概率密度函数和概率分布函数.

表1 ARL无偏的休哈特R图和改进的R图的参数值

1.2 ARL无偏的s控制图

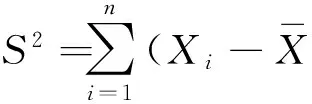
(5)

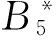
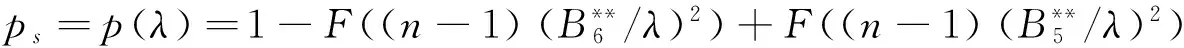
(6)

s控制图的ARL为Ls(λ)=1/p(λ). 当λ=1 时，由方程(6)可以得到

其中f和F分别为自由度为n-1的2分布的概率密度函数和概率分布函数.ARL无偏s控制图的上下控制限分别为：σ；σ.同理可得在α未知时参数为和.表2表示在第一类错误α下,参数值随n的变化趋势.图1b表示当n=10时,两种控制图的平均链长曲线,可以看出ARL无偏控制图无偏斜的平均链长曲线.

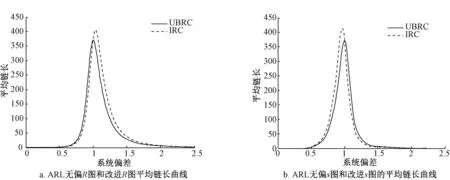
图1 当 n=10 时无偏的和改进的常规控制图的平均链长曲线Fig.1 Unbiased chavts and improved charts ARL profiles when n=10

2 数值比较

2.1 平均链长精确值的比较

可使用数值积分方法精确计算出控制图R图和s图的平均链长.标记σ0为标准差(σ0=1),σ为生产过程中发生偏差的标准差,δ(δ=σ/σ0)为偏差幅度.

表2 ARL无偏的休哈特s图和改进的休哈特s图的参数值

表3和表4分别给出在不同样本容量n和系统偏差δ下的控制图R图(UBRC和IRC)和控制图s图(UBSC和ISC)的平均链长.可以发现ARL无偏的R图和s图的平均链长最大值都在370,当系统偏差逐渐变小或变大时平均链长都会变小,并且随着样本容量的变大,监控更加灵敏.

表3 当最长平均链长为370下,随着系统误差的变化ARL无偏的R图和改进的R图的平均链长

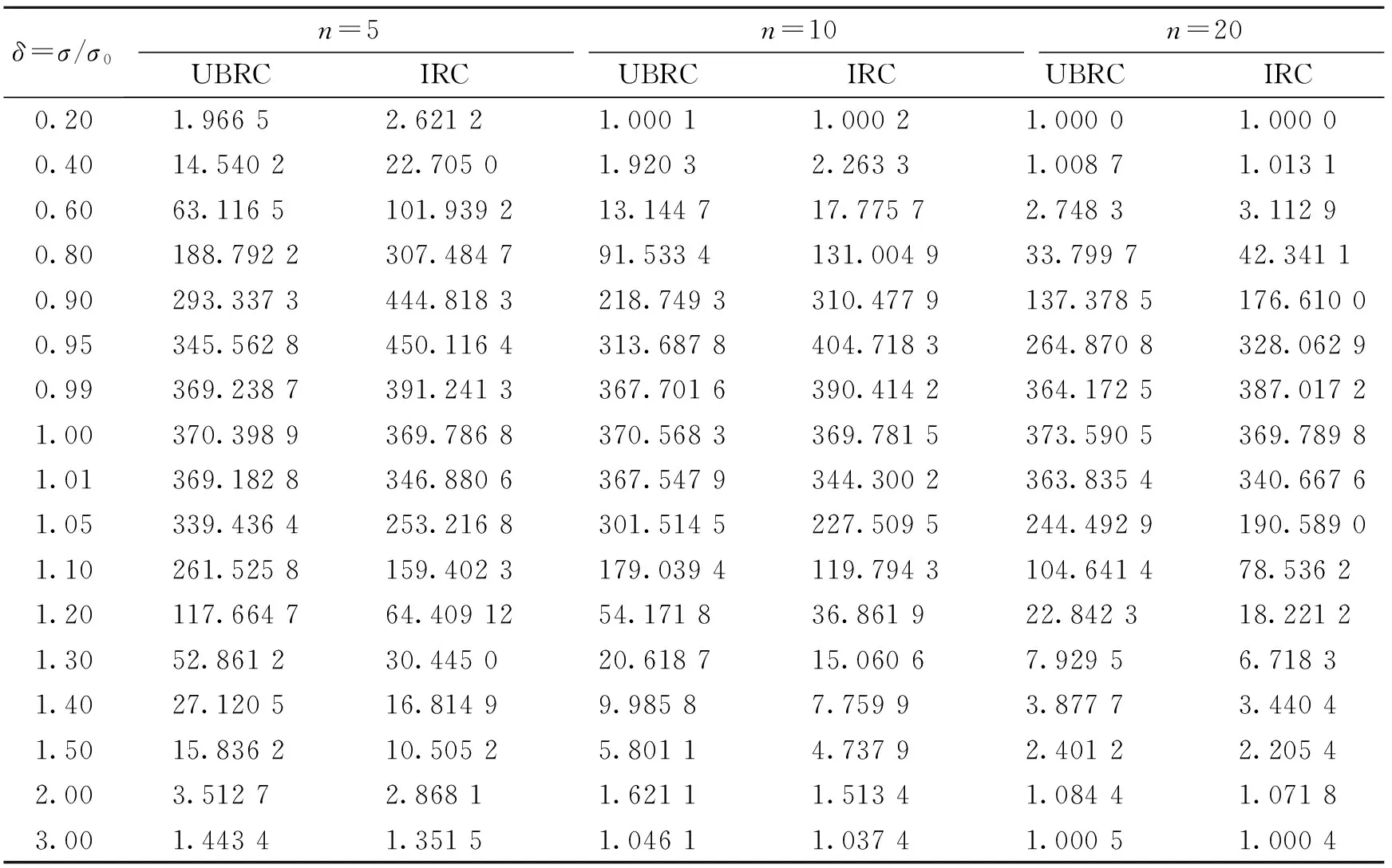
表4 当最长平均链长为370下,随着系统误差的变化ARL无偏的s图和改进的s图的平均链长

2.2 UBRC图和UBSC图的比较

对样本容量n=5,10,20时,ARL无偏的R图和s图的平均链长进行了比较,图2a，2b，2c中R图和s图的平均链长分别为

pR=p(σ)=1-G(D2σ)+G(D1σ)，即ARLR=1/pR,

(7)

ps=p(σ)=1-F((n-1)(B6/σ)2)+F((n-1)(B5/σ)2)，即ARLs=1/ps.

(8)

当n=5时,图2a给出了系统偏差σ从1到3的曲线.图2a中可以看到,当σ<1且逐渐趋近于1时,R图(UBRC)比s图(UBSC)有更短的平均链长，当σ>1且逐渐趋近于无穷时,UBSC控制图比UBRC控制图的平均链长减少速度更快,较快的减少速率代表检测水平更为敏感.对比图2a、图2b及图2c,随着样本容量的变大,两条曲线越来越趋近，当0.1<σ<1时,两条曲线几乎没什么区别，当σ>1时,UBSC图比UBRC更加有效.

图2d表示两个控制图平均链长的差,可以更直观地比较两个控制图平均链长.当n逐渐增大时,两个控制图的平均链长之差越来越小,当σ趋近无穷时,两个控制图平均链长几乎相等.将图2中四个图形比较可以发现,当样本容量足够大时，s图处处比R图能进行更有效的监测.当0.6<σ<1时,R图监测效果非常灵敏.原因在于公式(7)和(8)中两个微小的概率密度,它们的变化对平均链长之差产生很大的影响.当样本容量足够大时,s图比R图更有效，是因为R图只利用了样本最大值和最小值,没有利用所有统计量的信息.

图2 ARL无偏的休哈特R图和ARL无偏的休哈特s图的平均链长曲线Fig.2 Unbiased R and s chorts ARL profiles

3 对随机模拟数据的检验

在随机模拟中检测ARL无偏控制图的性能.随机模拟20组样本容量为10的变量,前10组是N(0,1)的独立同分布数据,后10组数据系统误差为δ=σ/σ0=2.图3中显示，ARL无偏控制图具有优秀的监控效果.

图3 ARL无偏控制图对随机数据的监控Fig.3 Unbiased ARL charts for monitoring simulated variance

4 结论

提出的“平均链长(ARL)无偏的休哈特控制图”及“控制图的ARL无偏性质”是对传统常规控制图的有效改进.通过数据显示,无偏控制图、常规控制图在σ=1时，均达到平均链长的最大值370，在监控生产过程中质量变化并无差异.而σ≠1时，随着σ的变化，无偏控制图平均链长逐渐减小,而常规控制图并无此优势.此外,在大样本容量下,通过比较ARL无偏的s控制图和ARL无偏的R控制图的平均链长,发现在质量控制中，ARL无偏s控制图更具有优势.

[1] KHOO M B C, LIM E G. An improvedR(range) control chart for monitoring the process variance[J]. Quality and reliability engineering, 2004, 21(1): 43-50.

[2] KHOO M B C. A modifiedschart for the process variance [J]. Quality engineering,2005, 17(4): 567-577.

[3] 宋宗伟，宋向东. 高产过程的CCC-r图控制限优化[J]. 辽宁工程技术大学学报，2014,33(4):535-538.

[4] 孙耀东，徐宝，赵志文. 固定设计下时间序列非参数回归模型的方差变点检验[J]. 郑州大学学报(理学版), 2014, 46(1): 1-4.

[5] 王海宇. 基于Bootstrap方法的分布未知情况下的小波动过程质量控制[J]. 郑州大学学报(理学版), 2014, 46(1): 63-67.

[6] 宋向东，宋宗伟. 监测过程均值小的偏移的综合控制图[J]. 郑州大学学报(理学版),2014, 46(1): 49-53

[7] ZHANG G. Improvedrandscontrol charts for monitoring the process variance[J]. Journal of applied statistics, 2014, 41(41): 1260-1273.

[8] 全国统计方法标准化技术委员会. GB/T 4091-2001常规控制图[S].北京：中国标准出版社，2001.

(责任编辑：方惠敏)

The Improvement ofRandsControl Charts

SONG Xiangdong, YANG Yi

(CollegeofScience,YanshanUniversity,Qinhuangdao066004,China)

The “average run length (ARL) unbiased control charts ofRands” and “unbiased ARL property of control charts” were proposed. Firstly, cumulative distribution function of the sample range was used to accurately solve standard deviation to control limits of control charts. Then,the quality changes of unbiased control charts and shewhart control charts were compared.The numerical examples showed that ARL unbiased control charts were more efficient in monitoring quality changes that emerged in production.

shewhartRchart; shewhartschart; average run length unbiased; cumulative distribution function

2016-09-07

宋向东(1965—)，男，河北保定人，副教授，主要从事非参数统计和质量控制研究，E-mail：Songxd@ysu.edu.cn; 通讯作者：杨仪(1991—)，男，山西临汾人，硕士研究生，主要从事质量控制研究，E-mail：yangyi--314@163.com.

O213.1

A

1671-6841(2017)01-0001-06

10.13705/j.issn.1671-6841.2016223