总体方差未知时k法单侧计量检验方案的改进

杜子芳，刘亚文，于焕杰

（1.中国人民大学 统计学院，北京 100872；2.对外经济贸易大学 统计学院，北京 100029）

0 引言

k法是产品计量抽样检验中的常用方法之一。对于其中的单侧检验而言，在中心极限定理成立假设下，其抽样检验方案（N，n，k）非常简单，只需要确定n和k两个参数即可。其中N为总体规模或批量，n是不放回简单随机抽样方式的样本量，k是单侧检验时的判别依据—界值。

单侧k法检验的现实背景是，μ0和μ1都是事先给定/规定/约定的值，分别称为合格质量水平和极限质量水平。由于单侧检验虽有下限与上限之分，但原理是一样的，不妨只讨论单侧下限的计量检验的情形，即认定当产品质量特性Y是数值型随机变量时，其总体均值μ≥μ0时，认为该批产品是合格的，买方应予以接收；总体均值μ＜μ1时，予以拒收。显然 μ越大越好，买方不希望μ＜μ0，更几乎不准 μ＜μ1。由于此时恒有(μ1＜μ0)，否则会因买方标准高于卖方标准，交易无法达成。但明显地，当总体均值 μ1≤μ＜μ0时，无法做出接收还是拒收的判断。为了对一批产品做出要么接收要么拒收的决断，基于第三方立场，人们提出了在μ1到μ0之间确定一个k值，修改检验或判定准则为：

1 方案改进

针对和总体方差σ2已知的情形（注意这既非罕见的场合，在连续生产许多批产品的中后期阶段尤其如此，亦非如统计学理论中的不符合现实的假设），W.A.Wallis上世纪50年代前就有十分完美的结果：

此即著名的Wallis经典公式。自该公式面世以来，国内外这方面的研究很少，国外近40年没见新的文献，幸而国内还有少数学者还在关注。

对于总体方差未知的情形（这种场合常见于孤立批和连续批的初期阶段，且十分吻合统计学的理论假设），Wallis W.A.于1947年也给出了一个看起来不错且沿用至今的近似结果：

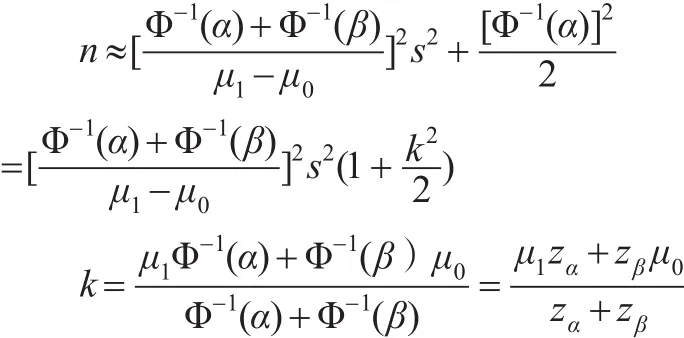
其推导过程为：

方差未知时应使用t分布解决问题，为此令：

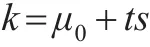
也就是：

当 μ=μ0时，P(yˉ≥μ0+ts)=1-α

当 μ=μ1时，P(yˉ≥μ0+ts)=β

或

当 μ=μ0时，P(yˉ-μ0≥ts)=1-α

当 μ=μ1时，P(yˉ-μ0≥ts)=β

进一步：

当 μ=μ0时

当 μ=μ1时

显然，μ=μ0时即服从自由度为n-1的中心t分布。

可是，μ=μ1时，由于不服从N（0，1）分布，从而服从自由度为n-1的非中心t分布。

方差为：

显然：

当 μ=μ0时

当 μ=μ1时

不过二者方差是相等的。

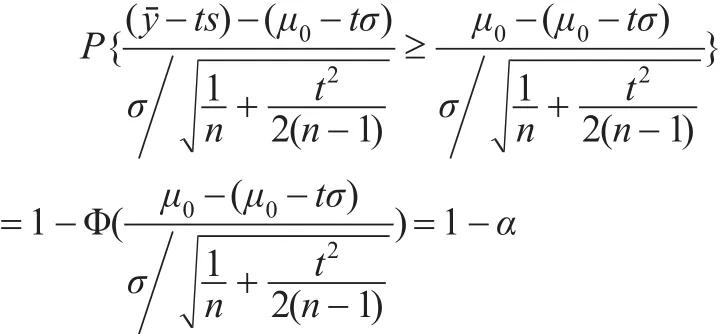
因而：

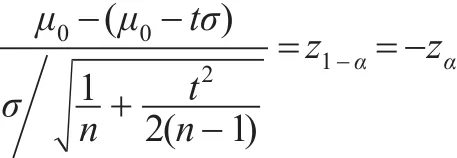
类似地也可得：

尽管这个结果只是近似的，且该公式一面世，哥伦比亚大学统计学教研组就指出这个结果远非准确，并以表的方式给出了一个具体比较。

然而令人讶异的是，这个公式竟然沿用至今，仍然活跃在国际标准和教科书中，似乎并未受到进一步的质疑和挑战。哥伦比亚大学统计学教研组的精确解主要从消除以正态分布近似t分布所产生误差的角度，并非给出一个相应的替代方案。事实上，1979年，E.C.Schilling和D.J.Sommer1979年还基于Wallis经典公式和近似公式制作了可用于对不合格品率或百单位缺陷数的检验用表，被用于ISO-3951-1981，并因此活跃于对新版ISO标准及各国标准之中。

症结在于，人们在几十年间里似乎没有发现上述推导过程一开始就令k=μ0+ts是一处不显眼的致命错误，因为仔细思考，从此式可以看出，k的定义只与μ0有关，而与 μ1无关，对比上述总体方差σ2已知时的公式 k=中，μ0与 μ1完全是对称的情形，则不难知道漠视μ1的存在是不合理的。

事实上，数理统计似乎总是以原假设成立为优先条件进行理论推导，不曾意识到对产品抽样检验来说，原假设与备择假设的地位是平等的，而且在计算过程里，忽视了本质上两个假设是允许同时成立的本原，否则Wallis经典公式便不成立。

将k法的下限计量检验的判定规则更“准确”地表达为：

原假设成立即当 μ=μ0时

备择假设成立即当 μ=μ1时

于是当总体/批方差σ2已知时，若服从标准正态分布；当 μ=μ1时也服从标准正态分布；则有：

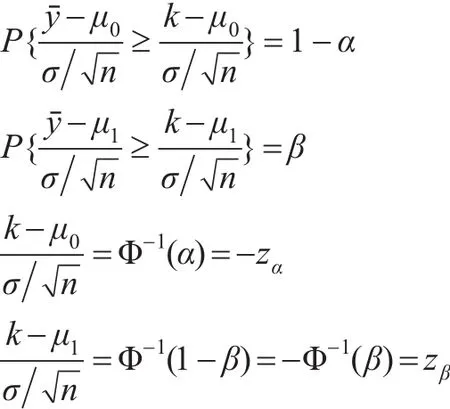
联立这两个方程即可得到优美无比的经典公式。换个角度看，这说明在单侧计量检验问题里原假设与备择假设的地位是平等的，允许同时成立。这与统计学的判别分析相似，基于这样的分析，可以给出一下推导：

设方差未知但相等，中心极限定理成立，将μ0与μ1一视同仁则：

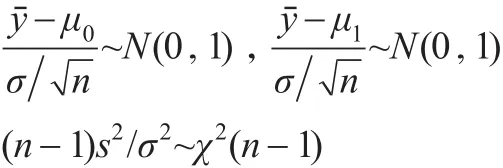
于是：

这里的公式极其简洁，完全可与总体方差已知时Wallis公式相媲美，且与Wallis公式的联系十分清晰，只是以t分布代替标准正态分布而已。从检索结果看，这个结果应归功于中国学者。需要注意的是，这是精确的结果，比起前述教科书的近似结果：不仅精确而且简洁，更容易解释。

美中不足的是：

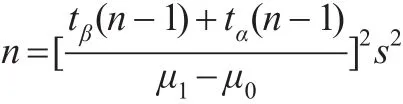
公式右边存在以n为自变量的参数，为了克服这一缺陷，国内学者提出的解决方法大致有三种：

（1）基于t分布与标准正态分布的近似关系，直观地提出了在Wallis公式中用样本方差替代了总体方差的解决办法；

（2）利用命名为动差法的解决办法，逐渐加大n进行试调查，直至样本方差稳定，然后在Wallis公式中用样本方差替代了总体方差；

（3）以假设值代入精确公式，算出相应参数的手段并编成表备查，现行国标即采用这种方法。

第一种解决方法实质是以标准正态分布近似代替t分布，样本量较小时弊端明显；第二种解决方法关于总体方差的估计误差较小，其样本量必偏大；第三种是目前最好的解决办法，但通过列出不同的有限的α，β等试算结果，编制成表让使用者查表，既不灵活也比较繁琐，更不适应当今计算机及软件普及的情况。

针对第三种解决方法的这一瑕疵，本文发现编制表格本质上属于迭代，所以完全可以尝试通过迭代法求得最终的n，步骤是：首先以 zα和 zβ代替 tα(n-1)和 tβ(n-1)，求出一个n*，将n*代入等式右端 tα(n-1)和 tβ(n-1)，求出新的n*；重复上述步骤直至n*稳定下来不再变化为止。尝试的结果表明，不论是初值是小还是大，不管离真值是远还是近，收敛速度都很快。究其原因，应是得益于t分布与标准正态分布的高度近似，比较t分布和标准正态分布图容易发现，两者差异的确不大，且差异随n增加而快速减小。见图1所示。

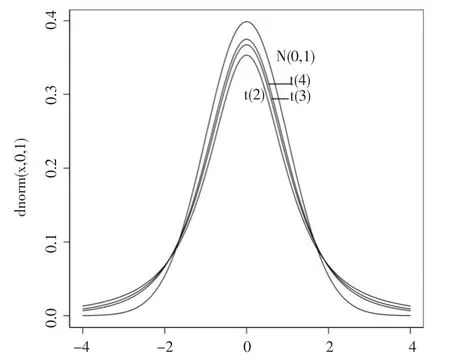
图1 标准正态分布与t分布密度曲线

2 数值模拟

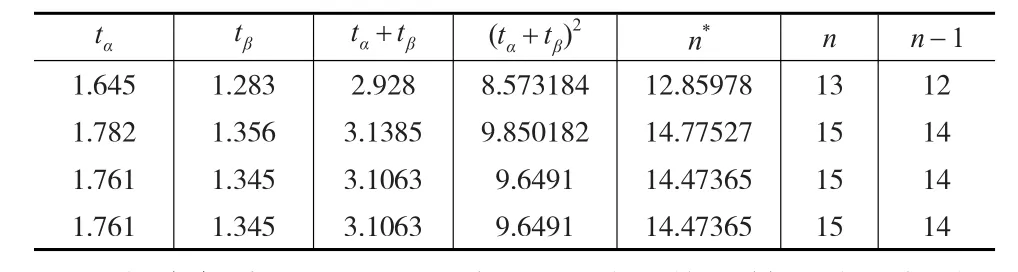
表1 第一例数值迭代过程表

在该例中，只经过三步即得到收敛的结果（见表1），且与依近似公式：

所得样本量结果一样，但t值有所不同，近似的为0.46，依精确公式计算的为0.470727。

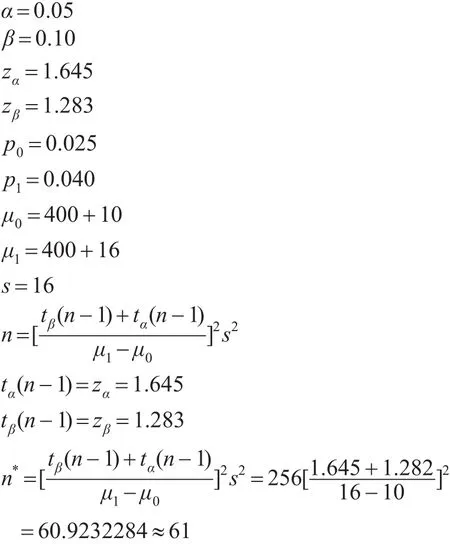
表2 第二例数值迭代过程表

如表2所示，3次迭代结果稳定于：

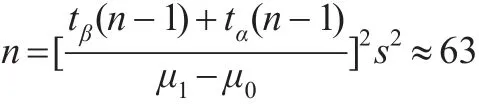
但若依近似公式则为：

可见，在方差较大时，即使需要比较精密的检验时，两者结果相差不大，这大概是Wallis近似公式能够“长盛不衰”的缘故。但当方差较小时，两者的差异是较大的：见表3所示，上例中的方差由256调到25，则依近似公式样本量是7，依精确公式迭代是11。

将这些例子的结果与哥伦比亚大学统计教研室的结果进行比较发现，精确公式比近似公式更加接近。其实由于Wallis近似公式：

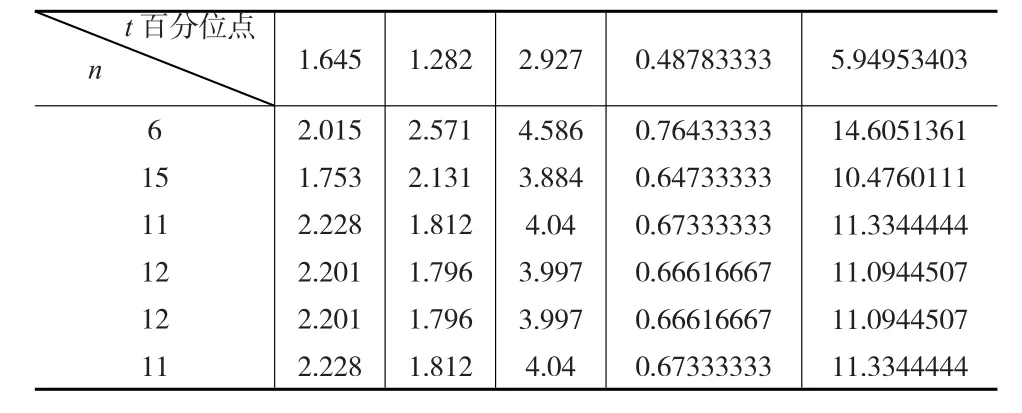
表3 方差较小时的数值迭代过程表

公式右端第二项是一个只与α有关的常数项，与n无关，不会像精确公式那样随n增加而收敛于总体方差已知的Wallis经典公式。这是很明显的瑕疵。瑕疵源于：

本文进一步发现，新的精确公式虽然结论正确，但推导过程却也存在瑕疵。原本的判定原则：

当μ≥μ0时，认为该批产品是合格的；

当μ＜μ1时，认为该批产品不合格。

与后来推出完美公式的k法的右侧计量检验的判定规则：

当 μ=μ0时，P{yˉ≥k}=1-α

当 μ=μ1时，P{yˉ≥k}=β

并不具一一对应的等价性，很明显，原本的规则中μ≥μ0和μ＜μ1都是实数轴上的一个区间，而后来的μ=μ0和μ=μ1都是一个点。更何况：

事实上，演算表明k与μ0之间的概率远小于理论上的0.5-α，足以表明所谓若服从标准正态分布的似是而非。

3 结论

样本量过大和过小都有弊端。如何合理确定样本量是产品抽查检验方案的重要内容之一。科学的抽查检验有助于公平维护卖方和买方双方的权益和利益，促进社会进步，减少交易纠纷，降低抽检成本。鉴于产品质量检验的重要性，对抽验方案的哪怕些微改进都是很有益处的，对于正处在经济转型产品升级由制造大国向制造强国奋进的中国来说，更具价值，附带地还可能有助于争取国际标准方面的话语权和存在感。同时，上面的推导虽然以产品检验为背景，但其方法可以推广与任何基于给定两类错误的如医学试验、风险控制等统计检验领域。

参考文献：

[1]Lieberman G J，Resnikoff G J.Sampling Plans for Inspection by Variables[J].Journal of the American Statistical Association,1955，(50).

[2]Lieberman G J.Tables for One-Sided Statistical Tolerance Limits[J].Industrical Quality Control,1958，14(10).

[3]Hamxker H C.Acceptance Sampling for Percent Defective by Variables and by Attributes[J].Journal of Quality Technology,1979，11(3).

[4]Wetherill G B.Sequential Methods in Statistics[J].Chapman and Hall,London,1975.

[5]于善奇.统计方法引论[M].北京：北京工业大学出版社，2014.

[6]于善奇.抽样检验与质量控制[M].北京：北京大学出版社，1991.

[7]于善奇.单侧限假设检验的理论与应用——GB/T14900—1994表3的设计方法[J].中国标准化，1996，（8）.

[8]杜子芳.多元统计分析[M].北京：清华大学出版社，2016.

[9]冯长根，惠宁利.抽样检验[M].北京：北京理工大学出版社，1992.

[10]厉晶晶，郭文.两类错误条件下的样本量选择[J].统计与决策,2010，（15）.

[11]刘建平.临床试验的样本含量的计算[J].中国中西医结合，2003,（7）.

[12]沈其君，徐勇勇.假设检验的基本概念[M].北京：高等教育出版社，2004．

[13]冯士雍,倪嘉勋,邹国华.抽样调查理论与方法[M].北京：中国统计出版社，1998.

[14]杜子芳.抽样技术及其应用[M].北京：清华大学出版社,1998.