基于时序分解的中国季度实物资金流量表的编制
2018-05-11黄靖贵
黄靖贵
(1.广西师范学院 混合与缺失数据统计分析广西高校重点实验室,南宁 530023;2.中央财经大学 统计与数学学院,北京 100081;3.广西壮族自治区统计局,南宁 530006)
0 引言
近年来,随着各国经济合作不断加强和金融市场全球化不断深入,通过观察国内外资本流动来判断本国的经济运行状况越来越受到各国的重视。作为国民经济核算体系的重要组成部分,社会资金流量统计以宏观经济视野来观察实体经济与金融经济的数量依存关系具有特殊的作用,为此国际上诸如美国、日本、加拿大和英国等国家早已分别于1945年、1954年、1961年、1963年开始编制发布了季度资金流量表,以满足本国短期宏观经济分析的需要。然而,中国官方公布资金流量表年度数据始于1992年,数据仍在不断修订中,而且季度数据迄今为止一直未公布,这明显落后于国际上许多其他主要国家。目前,根据我国各部门各行业的统计现状,及时收集获取编制资金流量表所需要的大量详细的GDP核算、财税收支、银行存贷款、保险费收及赔偿等各部门各专业统计基础资料仍存在很多困难,通过收集基础资料来编制出中国季度资金流量表难度则更大,为此探讨一套适合中国季度实物资金流量表数据的估算方法体系,以更简单、快捷的方式获取更及时、准确的统计数据,对分析中国短期经济运行情况具有重大意义。
1 时间序列分解模型
本文重点是借助时间序列分解方法理论来测算中国季度实物资金流量表,此处的“时间序列分解(temporal disaggregation)”与国内相关文献中提到的“时间序列分解”不同,这里的“时间序列分解”是指按照一定条件限制,将低频率的时间序列扩容成高频率的时间序列,扩容后的高频率时间序列与原序列性质保持一致,即假设{YT}(T=1,2,…n)是待分解的目标序列,要将其分解为时间频率更高的序列 {yt}(t=1,2,…s×n),YT=ysT-s+1+ysT-s+2+…+ysT,s表示分解类型,s=3、4、12分别表示将季度目标序列分解为月度序列、将年度序列分解为季度序列和将年度序列分解为月度序列,记 Y=(Y1Y2…Yn)′,y=(y1y2…ysn)′。而国内相关文献中提到的“时间序列分解”,是指将某一时间序列分解成趋势成分、季节成分、无法使用趋势和季节模式解释的随机干扰成分,比较常用的分解模型有乘法模型有加法模型。可见,两者在分解思想、分解方法和分解目标上存在本质性的差异。
国外学者对于本文重点讨论的“时间序列分解”已经做了非常广泛的研究,这些研究归纳起来主要分为非基于指示变量算法和基于指示变量算法两大类,第一类方法主要代表有:简单平均法、Lisman和 Sandee(1964)法、Boot-Feibes-Lisman(1967)一阶差分法和二阶差分法、Stram和Wei(1986)方法和样条插值法等等,第二类方法是以 Chow-Lin(1971)、Denton(1971)、Fernandez(1981)、Littelman(1983)、Guerrero(1990)共 同 发 展 起 来 的Chow-Lin法和Denton法为代表。在实践中,非基于指示变量的时间序列分解方法,由于只借助低频目标变量信息进行时间序列分解,分解结果往往无法描述时间序列的短期波动和季度波动,分解效果比较平滑,这与实际情况并不是特别相符,而基于指示变量时间序列分解方法,一方面可以基于高频辅助变量信息形成时序分解的假设条件,避免因主观因素建立与客观实际不符合的假设,另一方面可以合理充分利用各相关的经济信息和统计信息参与时序分解,分解结果更合理、有效和更有说服力,因此,该时间序列分解法在国际上引起了众多学者关注和普遍研究,也被认为使用最广泛、最成功的时序分解方法,本文基于此尝试编制中国季度实物资金流量表,以分析中国短期经济的运转情况,提高资金流量表对经济的预警时效性。
1.1 Chow-Lin时序分解法及Denton时序分解法
1.1.1 Chow-Lin方法
假设目标变量Ya和yq分别为n维的年度值列向量和m维的季度值列向量,m=n×4,指标变量Zq为z1,z2...,zq季度观测值的m×q矩阵,yq和Zq满足多元线性回归模型:

其中,β为q维回归系数列向量,uq为均值为0、协方差矩阵为Vq=E(uq)的m维随机列向量,称方程(1)为季度值回归方程。
由于yq未知,因此参数β无法估计,为此考虑根据特定的代数矩阵运算将季度值回归方程(1)转化成年度值回归方程,令B为将有m个季度的季度序列转化成n年的年度序列的m×n特定矩阵,定义为:

将 B′左乘到方程(1)两边,得:

令Ya=B′yq,Za=B′Zq,ua=B′uq,于是可得年度值回归方程:

其中,ua为均值为0,协方差矩阵为Va的n维随机列向量,Va=B′VqB。由此,根据广义最小二乘估计法可得模型的参数估计为:
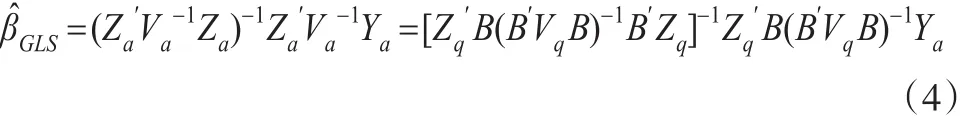
于是,将式(4)代入方程(1)可得目标变量的季度值估计为:

其中,(Ya-BZq)为年度值回归方程的残差序列,其被以VqB(B′VqB)-1的方式分配成季度值回归方程的残差序列
然而,在实际应用中,方程(5)中的协方差矩阵Vq往往是未知的,为确定Vq,所以做如下假设:
假设1:假设季度值回归方程的残差序列uq不存在自相关性,即若为n阶单位矩阵。方程(5)可表示为:
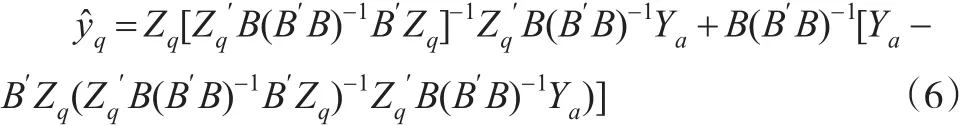
假设2:假设季度值回归方程的残差序列uq为AR(1)过程,即满足方程:


同时,假设年度值回归方程的残差序列ua也为AR(1)过程,即满足方程:


于是,由式Va=B′VqB可知,q值等于矩阵B′VqB的第1行第2列元素与第1行第1列元素的比值,为:
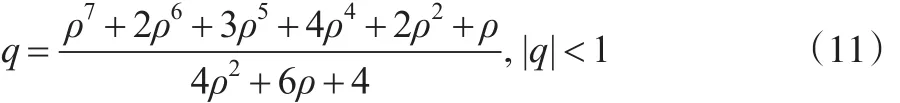
为此可以通过如下迭代法求得ρ值。首先,给定q初始值,求解多项式(11)绝对值小1的实数根 ρ,并代入式(8)得到矩阵Vq,然后再依次通过式(9)估计,通过方程(3)求得年度残差ua,通过自相关模型(9)求得q值,重复以上过程,直至ρ值几乎不变为止,最后确定Vq。
1.1.2 Denton方法
Denton(1971)方法是基于BFL方法的基础上改进得来的,其主要思想与Chow-Lin方法思想有很多相似的地方,它在将目标变量年度值分解为季度值的过程中,也是依赖于其他变量作为指标变量进行协助分解。具体地,首先,假设惩罚函数:
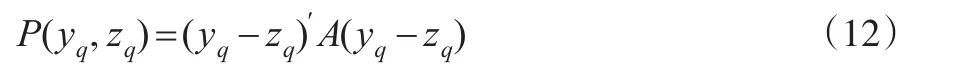
并使yq满足:
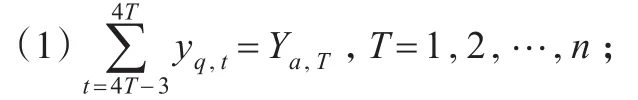
(2)惩罚函数值 P(yq,zq)最小。
然后,构建拉格朗日函数:
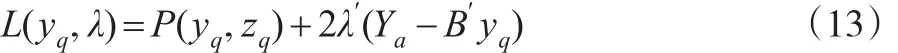
求L(yq,λ)关于 yq和 λ的偏导数,并令其等于0,整理后得:

其中,r=Ya-B′zq,A为n×n矩阵,B矩阵与前述一样。
最后,由式(14)可得:

然而,在实际应用中,式(15)中的矩阵A是未知的,为此做如下假设:
假设1:假设 A=Im×m,则根据式(15)有:

式(16)结果与Chow-Lin方法假设1的结果是一致的,即其通过把目标变量与指示变量年度数值的回归残差序列平均分散成季度数值的回归差残差序列,从而达到使惩罚函数最小的目的。
假设2:假设惩罚函数P(yq,zq)为目标变量一阶差分减去指示变量一阶差分之差的平方和,即:

为确保向后差分 t=1时,△yq1=yq1-yq0,△zq1=zq1-zq0,yq0和 zq0不超出时间序列范围,规定△yq1-△zq1=△(yq1-zq1)=yq1-zq1。于是,P(yq,zq)以矩阵形式可以表示为:

记式(18)为DAFD方法。其中:

由此不难发现,惩罚函数P(yq,zq)为目标变量与指示变量各自一阶差分后相减的平方和时,式(12)中的A为A=D′D。进一步地,若惩罚函数为目标变量与指示变量各自二阶差分后相减的平方和时,即 P(yq,zq)=时,式(12)中的 A 为A=D′D′DD,记该方法为DASD方法,依此类推,若惩罚函数为目标变量与指示变量各自多次差分后相减的平方和时,式(12)中的A为 A=D′D′…D′DD…D 。
另外,Denton(1971)还从目标变量和指示变量的比例关系来对惩罚函数P(yq,zq)定义,假设其为目标变量和指示变量相对量差异的函数,即:

其中,Z 为对角线上元素分别为 zq,1,zq,2,…zq,4n的4n×4n矩阵。类似地,还可以假设其为的函数(记为DRFD方法)或的函数(记为DRSD方法)等。为了估计出yq值,可以通过类似上述方法,构建拉格朗日函数,求出yq的估计值为:
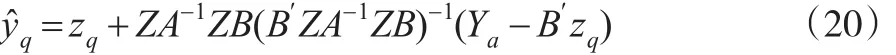
1.2 时间序列分解效果评价
国际上对时间序列分解模型的研究非常广泛,Baoline Chen(2007)归纳了以下五大检验标准:
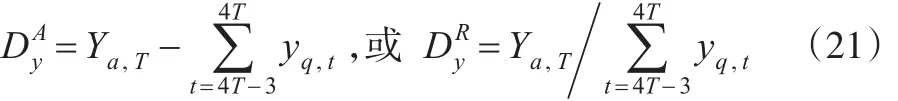
标准2:最终分解结果应尽可能地保持指示变量序列的短期波动,定义的检验测度为:

标准3:最终分解结果位于度年度间间断点两侧出现剧烈失真或扭曲情况,定义的检验测度为:

标准4:最终分解结果位于序列首尾两端出现不连续性或剧烈扭曲情况,定义的检验测度为:

标准5:如果序列中存在同期限制,最终分解结果应同时满足同期限制和年度限制。对于多变量序列...,yqm,T,同期限制为…,T;年度限制为已知,i=1,2,…,m。为此除了按标准1进行年度限制检测外,还做同期限制检测:

2 中国季度实物资金流量表的编制
2.1 矩阵式资金流量表结构
资金流量矩阵是社会核算矩的重要组成部分,它实际上是为了将全部社会资金的流向、流量及部门间的资金联系勾勒起来而把各机构部门的国民收入账户与资金流量账户合并成一张非常简明的资金流量表,通过这张表可以观察整个国民经济资金流动的全貌。目前中国官方是以账户式(标准式)结构形式来公布中国实物资金流量数据的,为更于对中国季度实物资金流量表进行测算,本文先对现有的资金流量表做简化处理,部门分类上,主要把国外部门合并到国内部门中去,交易项目上,主要是把财产性收支与转移收支中的细项省略掉,并将其转换成矩阵式的资金流量表如表1所示,其由W 、U1、U2、Y、GS、R1、R2、V、FS、Z、S、GU和FU等共13个子矩阵或向量组成,每个矩阵的每个元素都有双重意义,从横行方向看是表示收入,从纵列方向看是表示支出,如对于矩阵W的任意一个元素wij,其表示的是部门i从部门 j获得的资金数量,也表示部门 j运用在部门i的资金数量。

表1 矩阵式资金流量账户的基本结构
表1中的矩阵U1、U2、Y 、R1、R2、Z′和S存在平衡关系:(1)总收入=初次分配收入+再分配收入+增加值,即;(2)总支出=初次分配支出+再分配支出+可支配收入使用,即;(3)总收入=总支出,即:GS=GU′;(4)增加值合计=可支配收入使用合计,即;(5)分配收入合计=分配支出合计,即:;(6)每项交易项目收入合计=每项交易项目支出合计,即
2.2 目标变量、指示变量的选择及其数据来源
编制中国季度实物资金流量表时,本文需要从Chow-Lin、DAFD、DASD、DRFD和DRSD这5种方法中选择最优的方法对矩阵U1、U2、Y、GS、R1、R2、Z、S和GU中共34个目标变量的年度时序列进行时间序列分解,分解时所需要的季度指示变量是根据国家统计局编制的《中国实物资金流量表编制方法》对各机构部门、各交易项分类以及所要求的基础资料来源做适当整理得到的,具体的目标变量及其对应的指示变量选择如下页表2所示。本文考虑到指示变量的可获取性,仅对2006—2014年中国实物资金流量表的年度数据进行季度分解。
2.3 时序分解效果检验及最终方法选择
为选择最优的时序分解方法,本文采用R软件先分别根据Chow-Lin、DAFD、DASD、DRFD和DRSD这5种方法对34个目标变量的年度序列进行分解,然后再根据前述提到的五大检验标准对各最终分解结果进检验,比较每种分解方法的分解效果,从中选择最合适的方法作为测算中国季度实物资金流量表的时序分解方法。对34个目标变量的最终分解结果进行分解效果检验时,由于每个序列对应的每个检验标准都存在一定的差异,为了便于比较,本文对此做了平均化处理,最终检验结果如后文表3所示,从中可以发现,五种方法对34个目标变量的最终分解都满足分解年度限制的基本要求;从保持指示变量的短期波动情况来看,Chow-Lin分解方法最好,其次是DRFD分解方法,最差的是DASD分解方法;从年度间间断点两侧分解失真或扭曲的程度来看,扭曲程度最小的前三者分别是DRSD方法、DRFD方法和Chow-Lin方法,三者的扭曲程度都比较小;年中间分解扭曲程度最小的Chow-Lin分解方法,值仅为0.00917;从最终分解的开头季度的扭曲程度来看,扭曲程度最小的是Chow-Lin方法,其----BB值为0.04147,最大的是DRSD方法,其值为0.32899;从最终分解的末季扭曲程度来看,扭曲程度最小的前两种方法是DRFD方法和Chow-Lin方法,其扭曲程度都在2%以内。对于第五大标准的检验,由于本文考虑的目标变量不存在同期限制,所以在此不做检验。从总体上看,Chow-Lin分解方法最终的分解效果最好,其次是DRFD方法,为此本文选择Chow-Lin分解方法作为编制中国季度实物资金流量表的最终分解方法。
2.4 季度实物资金流量表编制及编制结果
根据矩阵式资金流量表各子矩阵的平衡关系以及使用Chow-Lin分解方法对2006—2014年年度实物资金流量数据进行分解的最终结果,依次对每年每个季度的子矩阵Y、U2、R1、U1、GS、R2、Z、GU 和S进行填写,其中对于增加值矩阵Y,先根据时序分解结果填写非金融部门、金融部门、政府部门及各部门合计的劳动者报酬、生产税净额、增加值合计后,再根据Y矩阵的内部平衡关系依次填写住户部门的增加值合计、劳动者报酬和生产税净额,最后填写各个部门的营业盈余;对于矩阵U2,先根据时序分解结果填写非金融部门、金融部门、政府部门及各部门合计的转移性收入,最后再填写住户部门的转移性收入;对于矩阵R1,各部门的劳动者报酬和生产税净额则根据矩阵Y的结果填写,财产性支出先根据时序分解结果填写非金融部门、政府部门、住户部门及各部门合计的数据,最后填写金融部门的数据;对于矩阵U1,劳动者报酬只有住户部门得到,生产税只有政府部门得到,这两个数根据R1各部门的劳动者报酬和生产税净额合计填写,财产性收入则先根据时序分解结果填写非金融部门、政府部门、住户部门及各部门合计的数据,再填写金融部门的数据;对于矩阵R2,先根据时序分解结果填写非金融部门、金融部门、住户部门及各部门合计的转移性支出,最后再填写政府部门的转移性支出;对于矩阵Z,则除了住户和政府部门有最终消费外,其他部门都没有,其消费数据根据时序分解结果填写;GU根据GS填写;最后S矩阵根据GU、R1、R2和Z填写,从而得到资季度资金流量矩阵的编制结果,其中,各机构部门从季度增加值中获取劳动者报酬如图1所示。

表2 目标变量及其对应的指示变量

表3 Chow-Lin分解法和Denton分解法分解效果检验

图1 2006—2014年各机构部门季度获取劳动者报酬变化趋势
从图1中可以发现,从长期总体趋势看,各机构部门得到的劳动者报酬都呈明显的增加态势,其中增长最快的是金融企业部门,2006—2014年,金融企业部门从增加值中得到的劳动者报酬收入年均增长速度为20.4%,同期非金融企业部门和住户部门从增加值中得到的劳动者报酬收入年均分别增长15.6%和14.3%,政府部门从增加值中得到的劳动者报酬收入年均增长仅为12.9%。从季度的波动情况看,2006—2014年,各机构部门所创造的增加值中劳动者报酬的季度变化都存在着非常明显的差异,其中非金融企业部门于2010年后每年第一至第三季度的劳动报酬都比较低,第四季度最高并且很明显,出现这种情况的可能原因是与非金融企业部门逐年加大绩效工资发放有关。此外,从图中还可以发现,2013年第一至第三季度非金融企业部门的劳动者报酬收入都比2012年同期的明显低,而到了第四季度又出现较大幅度反弹现象,究其原因,主要是由于2012年12月份中央出台“八项规定”影响,表现为一方面由于某些行业生产经营受到了明显冲击,如餐饮行业特别是中高档餐饮行业,据国家统计局发布的数据显示,2013年第一季度社会消费品零售总额中的限额以上企业餐饮收入同比下降了2.6%;另一方面原因是“中央八项规定”刚出台时,许多非金融企业对文件进行了过度解读而少发或停了职工的正常福利,甚至有的企业借“中央八项规定”之名故意减少了职工的工资,从而引起了2013年前三季度非金融企业部门的劳动者报酬收入出现下滑的趋势。但是,随着时间的推移,企业对“中央八项规定”有了正确认识后才补发之前未发的职工正常福利和故意减少的工资,因此才出现非金融企业的劳动者报酬于2013年第四季度发生明显反弹的现象,特别是2014年7月份全国总工会发文对企业职工正常福利做出了明确规定后,非金融企业的劳动者报酬才恢复2014年以后正常轨道上来。
2006年第一季度至2014年第四季度,金融企业部门和住户部门的劳动者报酬收入,两者都呈现出明显的季节性变化规律,并且它们的变化幅度都是随着收入水平的提高而出现扩大的趋势。但是,从年内的变化特点来看,它们的变化特征存在着明显不同,其中金融企业部门年内的劳动者报酬收入主要是呈现两头季度高中间季度低的“V”型态势,而住户部门则出现逐季增加的态势,因为住户部门从自身得到的劳动者报酬其中大部分来自于农村住户,因此我国农业生产活动的季度化规律很大程度上决定了其季节性变化规律的特点。对于政府部门而言,在2006—2014年,除了2014年第三季度之外,各季度的劳动者报酬收入很平稳,这主要由我国公职人员流动性不大和工资收入比较稳定所决定,但是,2014年第三季度政府部门的劳动者报酬收入出现偏高,这主要原因是2014年后由于很多地方的公务员绩效考评与奖金挂钩,当年绩效考评完成后发放的奖金一般都比较集中于下年的第三季度。
3 结论
季度实物资金流量统计数据是以宏观经济视野观察短期实体经济关系的重要基础,但是,编制季度实物资金流量表需要基础资料非常多且复杂,编制工作难度大,至今还无法直接从官方公布的统计资料中得到季度实物资金流量统计数据。本文从我国官方发布有限的信息资料出发,利用Chow-Lin时序分解方法和Denton时序分解方法对我国年度实物资金流量数据进行分解比较研究,结果发现Denton时序分解方法虽然计算过程比较便捷、稳定,但Chow-Lin分解方法更能保持指示变量的短期波动性,分解结果在年度间间断点两侧及首尾处分解结果失真或扭曲程度比较小,而且分解结果能够合理地反映我国经济季度运行情况,因此,本文认为Chow-Lin分解方法更适合作为测算我国季度实物资金流量表数据的时序分解方法,为此本文利用其最终分解结果试编制了我国季度实物资金流量表,并依此做了简要分析,这为对我国深入研究季度实物资金流量估算方法指明了方向。
参考文献:
[1]Almon C.The Craft of Economic Modeling[J].Boston:Ginn Press,1988.
[2]Boot J C B,Fiebes W,Lisman J H C.Further Methods of Derivation of Quarterly Figures from Annual Data[J].Applied Statistics,1969,(16).
[3]Chen B.An Empirical Comparison of Methods for Temporal Distribution and Interpolation at the National Accounts[J].Bureau of Economic Analysis,2007.
[4]Chow G C,Lin A,Best Linear Unbiased Interpolation,Distribution and Extrapolation of Time Series by Related Series[J].Review of Economics and Statistics,1971,(53).
[5]Denton F T.Adjustment of Monthly or Quarterly Series to Annual Totals:An Approach Based on Quadratic Minimization[J].Journal of the American Statistical Association,1971,(66).
[6]Fernandez R B.A Methodological Note on the Estimation of Time Series[J].Review of Economics and Statistics,1981,(63).
[7]Guerrero V M.Temporal Disaggregation of Time Series:An ARIMA-based approach[J].International Statistical Review,1990,(58).
[8]Lisman J H C,Sandee J.Derivation of Quarterly Figures From Annual Data[J].Applied Statistics,1964,(13).
[9]Marcellino M.Some Consequences of Temporal Aggregation in Empirical Analysis[J].Journal of Business and Economics Statistics,1999,(1).
[10]Abeysinghe T,Lee C.Best Linear Unbiased Disaggregation of Annual GDP to Quarterly Figures[J].Journal of Forecasting,1998,(1).
[11]Stram D O,Wei W W S.A Methodological Note on the Disaggregation of Time Series Totals[J].Journal of Time Series Analysis,1986.
[12]Wei W W S,Stram D O.Disaggregation of Time Series Models[J].Journal of the Royal Statistical Society,Series B,1990,(52).
[13]许宪春.利用GDP进行国际比较需要注意的若干问题[J].经济与管理研究,2007,(5).
[14]许宪春.中国国民经济核算中的若干重要指标与有关统计指标的比较[J].世界经济,2014,(3).
